Magnetic Field of a Toroid Using Ampere's Law

This page explains how to use Ampere's Law to solve for the magnetic field of a toroid.

Magnetic Field of a Toroid using Ampere's Law

Using Ampere's Law simplifies finding the magnetic field of a toroid since using the Biot-Savart law would be extremely difficult due to having to integrate over all the current elements in the toroid.

Geometry of a Toroid

A toroid is essentially a solenoid whose ends meet. It is shaped like a doughnut (the base shape does not need to be a circle; it can be a triangle, square, quadrilateral, etc.), is symmetrical around an axis of rotation, and contains N loops around a closed, circular path with a radius of r inside of its loop. Mathematically, it can be described as an object or surface generated by revolving a closed plane around an external axis that is parallel to it so it does not intersect. Toroids are commonly used as electronic compartments since they generate a magnetic field or frequency depending on the material of the ring and the type of wire and the number of loops the wire is wound around the ring.

A Mathematical Model

First we start with solving the path integral from Ampere's law:

[math]\displaystyle{ {\oint\,\vec{B}•d\vec{l} = μ_{0}∑I_{inside&ensp;path}} }[/math]

The magnetic field, [math]\displaystyle{ {\vec{B}} }[/math], is, due to the symmetry of a toroid, constant in magnitude and always tangential to the circular path (i.e. parallel to [math]\displaystyle{ {d\vec{l}} }[/math]). The path of a toroid is circular, so [math]\displaystyle{ {\oint\,d\vec{l}} }[/math] is equal to [math]\displaystyle{ {2πr} }[/math]. Therefore, the path integral of the magnetic field is equal to [math]\displaystyle{ {B2πr} }[/math]. The amount of current piercing the soap film (i.e. [math]\displaystyle{ {∑I_{inside&ensp;path}} }[/math]) is [math]\displaystyle{ NI }[/math], where [math]\displaystyle{ N }[/math] is the number of piercings (i.e. turns in the coil) and [math]\displaystyle{ I }[/math] is the current. Ampere's law is now this:

[math]\displaystyle{ {B2πr = μ_{0}NI} }[/math]

From this, we can solve for the magnetic field for a toroid:

[math]\displaystyle{ {B = \frac{μ_{0}NI}{2πr}} }[/math]

Examples

Simple

A toroid frame is made out of plastic of small square cross section and tightly wrapped uniformly with 100 turns of wire, so that the magnetic field has essentially the same magnitude throughout the plastic (radius R of the curved part is much larger than cross section width w). With a current of 2 A and radius of 5 m, what is the magnetic field inside the plastic.

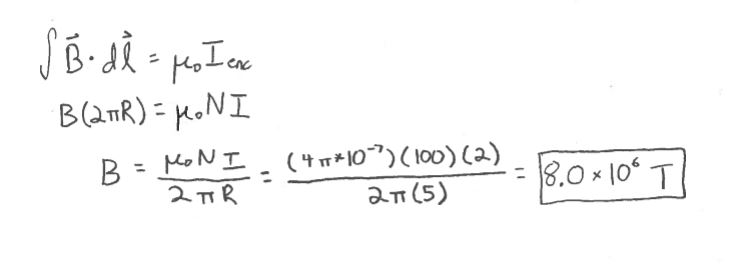
Middling - Difficult

The toroid shown in the diagram has an inner radius of [math]\displaystyle{ R_{i} }[/math] and an outer radius of [math]\displaystyle{ R_{o} }[/math] and is centered at the origin in the diagram. The z-axis passes through the center of the doughnut hole. This toroid is wrapped with [math]\displaystyle{ N }[/math] loops of current [math]\displaystyle{ I }[/math] flowing up the outside surface of the toroid, radially inward, down the inner surface, and then radial outward. Assume that the magnetic field produced by this toroid has the form [math]\displaystyle{ \vec{B} = B(r,z)\hat{φ} }[/math] at every point in space where [math]\displaystyle{ r }[/math] is the perpendicular distance from the z-axis and [math]\displaystyle{ \hat{φ} }[/math] is a unit vector which "curls" around the z-axis, i.e., it is always tangent to any circle with rotational symmetry around the z-axis.

Middling

(a.) Consider a z-axis centered Amperian loop in the plane of the toroid, at [math]\displaystyle{ z = 0 }[/math], with a radius [math]\displaystyle{ r \lt R_{i} }[/math] and use it to find the magnitude of the magnetic field inside the inner radius of the toroid.

(b.) Consider a z-axis centered Amperian loop in the plane of the toroid, at [math]\displaystyle{ z = 0 }[/math], with a radius [math]\displaystyle{ r \gt R_{o} }[/math] and use it to find the magnitude of the magnetic field inside the inner radius of the toroid.

Difficult

(c.) Consider a z-axis centered Amperian loop in the plane of the toroid, at [math]\displaystyle{ z = 0 }[/math], with a radius [math]\displaystyle{ R_{i} \lt r \lt R_{o} }[/math] and use it to find the magnitude of the magnetic field inside the inner radius of the toroid.

(d.) Consider a z-axis centered Amperian loop far above the toroid [math]\displaystyle{ z \gt \gt R_{o} }[/math], with a radius [math]\displaystyle{ R_{i} \lt r \lt R_{o} }[/math] and use it to find the magnitude of the magnetic field far above the toroid.

Another Example

(a.) Derive the formula for the magnitude of the magnetic field inside a coil that has the shape of a torus whose minor radius is much smaller than the length of the central circle. The toroidal coil has [math]\displaystyle{ N }[/math] turns per unit length and current [math]\displaystyle{ I }[/math] flows through it.

Solution:
We determine the magnitude of the magnetic B-field by using Ampere’s law

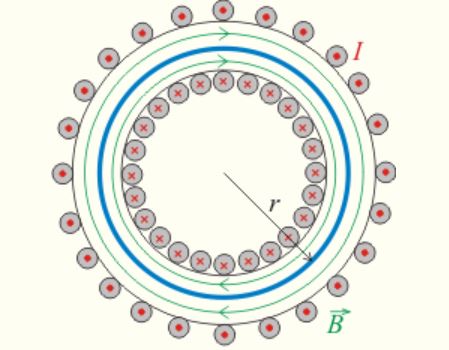
[math]\displaystyle{ {\oint\,\vec{B}•d\vec{l} = μ_{0}∑I_{inside&ensp;path}} }[/math]

We chose a circle running through the center of the hole of the toroid for Ampere’s loop. The length of this circle is

[math]\displaystyle{ {l ={2πr}} }[/math]

The total current flowing through the circle bordered by the Ampere’s loop is

[math]\displaystyle{ {I_{c} = NlI = {2πr}NI} }[/math]

The magnetic field vector [math]\displaystyle{ B }[/math] is parallel to the vector of the length element [math]\displaystyle{ dl }[/math] all the way around the integration path. Thus we can express the right-hand side of Ampere’s law as

[math]\displaystyle{ {\oint\,\vec{B}•d\vec{l} = B{2πr}} }[/math]

The left-hand and the right-hand sides of the Ampere’s law must be equal and we can express the magnitude of the [math]\displaystyle{ B }[/math]-field as

[math]\displaystyle{ {B2πr ={μ_{0}NI}{2πr}} }[/math]

[math]\displaystyle{ {B ={μ_{0}NI}} }[/math]

The final answer is then [math]\displaystyle{ {B ={μ_{0}NI}} }[/math].

Magnetic Field of a Toroid Using Ampere's Law

Contents