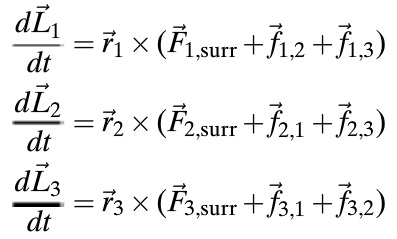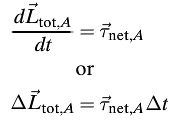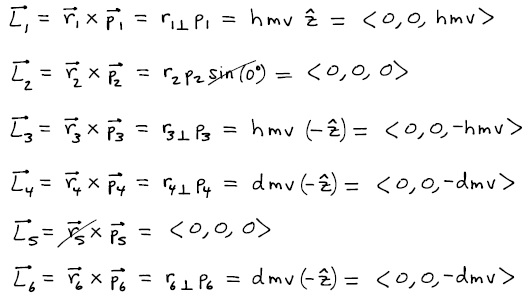Angular Momentum of Multiparticle Systems: Difference between revisions
No edit summary |
|||
| (16 intermediate revisions by the same user not shown) | |||
| Line 3: | Line 3: | ||
==Main Idea== | ==Main Idea== | ||
[[The Angular Momentum Principle]] may be extended to a multiparticle system to provide various insights, such as an explanation for the counter-intuitive behavior of [[Gyroscopes]]. This page details how one could derive the angular momentum principle of a multiparticle system and provides a few examples to illustrate the concept. | [[The Angular Momentum Principle|The angular momentum principle]] may be extended to a multiparticle system to provide various insights, such as an explanation for the counter-intuitive behavior of [[Gyroscopes|gyroscpoes]]. This page details how one could derive the angular momentum principle of a multiparticle system and provides a few examples to illustrate the concept. | ||
===Mathematical Model=== | ===Mathematical Model=== | ||
| Line 25: | Line 25: | ||
===Computational Model=== | ===Computational Model=== | ||
[[File:Vpython screenshot.jpg|none| | |||
[[File:Vpython screenshot.jpg|none|thumb|500px|VPython Screenshot]] | |||
[https://trinket.io/glowscript/88ddf42892 Glowscript Trinket Example] | [https://trinket.io/glowscript/88ddf42892 Glowscript Trinket Example] | ||
| Line 34: | Line 36: | ||
===Simple=== | ===Simple=== | ||
'''Question:''' | |||
::What is the total angular momentum ''L''<sub>tot</sub> of a system of particles with individual angular momenta ''L''<sub>1</sub> = <0,0,10>, ''L''<sub>2</sub> = <0,0,-5>, & ''L''<sub>3</sub> = <0,0,15>? | |||
'''Answer:''' | |||
::''L''<sub>tot</sub> = <0,0,20> | |||
===Difficult=== | ===Difficult=== | ||
| Line 50: | Line 60: | ||
==Connectedness== | ==Connectedness== | ||
This concept is highly interesting because of its part in describing highly complex systems and interactions on various scales, as multi-component systems exist on all scales from quantum to cosmic. Being in MSE, it may be of interest to investigate materials as multi-component systems, and to apply the angular momentum principle in this manner. | |||
==History== | ==History== | ||
[[The Angular Momentum Principle#History|''See: History of the Angular Momentum Principle'']] | |||
== See also == | == See also == | ||
| Line 78: | Line 87: | ||
==References== | ==References== | ||
Matter & Interactions, Vol. I: Modern Mechanics, 4nd Edition by R. Chabay & B. Sherwood (John Wiley & Sons 2015) | |||
[[Category: Angular Momentum]] | [[Category:Angular Momentum]] | ||
Latest revision as of 04:33, 5 December 2015
By Jonathan Peraza (jonperaza)
Main Idea
The angular momentum principle may be extended to a multiparticle system to provide various insights, such as an explanation for the counter-intuitive behavior of gyroscpoes. This page details how one could derive the angular momentum principle of a multiparticle system and provides a few examples to illustrate the concept.
Mathematical Model
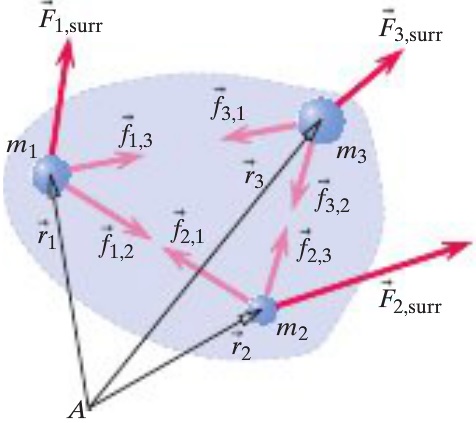
The derivation of the angular momentum principle of a multiparticle system is most easily understood when following a simple example, in this case we will work with a three particle system:
- The angular momentum principle is written for each individual particle relative to location A, with position vectors r and external force vectors F.
- The individual equation is then summed. Note that, due to the reciprocation of forces, the internal forces f cancel out.
- The equation is now rewritten with the right side, representing net torque, as τnet,A
Computational Model
Examples
Simple
Question:
- What is the total angular momentum Ltot of a system of particles with individual angular momenta L1 = <0,0,10>, L2 = <0,0,-5>, & L3 = <0,0,15>?
Answer:
- Ltot = <0,0,20>
Difficult
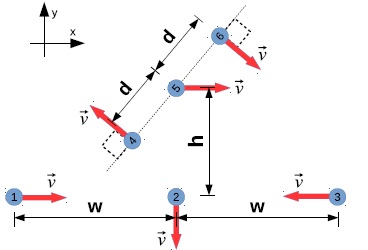
Each of the six particles in the figure have identical mass m and moves in the x-y plane with the same speed v as indicated in the diagram. Take the location of particle 5 as the reference point for all angular momentum calculations when answering the following questions.Be sure to express your answer as a vector.
- What is the momentum of the individual particles?
- Consider the particles above as a single multiparticle system. With respect to particle 5, what is the total angular momentum of the system? What is the translational angular momentum? What is the rotational angular momentum?
Connectedness
This concept is highly interesting because of its part in describing highly complex systems and interactions on various scales, as multi-component systems exist on all scales from quantum to cosmic. Being in MSE, it may be of interest to investigate materials as multi-component systems, and to apply the angular momentum principle in this manner.
History
See: History of the Angular Momentum Principle
See also
The Angular Momentum Principle
Multi-particle Analysis of Momentum
External links
The Momentum Principle in Multi-Particle Systems (Video)
Angular momentum of a multi-component system
Chapter 19 Angular Momentum, MIT Course Materials
References
Matter & Interactions, Vol. I: Modern Mechanics, 4nd Edition by R. Chabay & B. Sherwood (John Wiley & Sons 2015)