Speed of Sound in a Solid: Difference between revisions
(Created page with "PLEASE DO NOT EDIT THIS PAGE. COPY THIS TEMPLATE AND PASTE IT INTO A NEW PAGE FOR YOUR TOPIC. Short Description of Topic Contents [hide] 1 The Main Idea 1.1 A Mathematical...") |
|||
| (31 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
This page discusses calculating the speed of sound in various solids and provides examples of such calculations. | |||
Claimed by Dpatel322 @ 12/1 | |||
==The Main Idea== | |||
The speed of sound is the speed that sound wave travels through a particular medium. In comparison to air, sound travels considerably faster in solids. The speed that sound travels in various solids depends on the solid's density and elasticity, as these factors effect the ability of the sound waves vibrational energy to transfer across the solid medium. | |||
The | |||
A Mathematical Model | ===A Mathematical Model=== | ||
The speed of sound in solids <math> {V_{s}} </math> can be determined by the equation. Young's Modulus is a measure of elasticity of an object, and it can be computed to solve for interatomic values, such as interatomic bond stiffness or interatomic bond length. | |||
<math> {V_{s}} = d* √ (K_{s}/m_{atom}) </math> | |||
<math> d </math> = interatomic bond length | |||
<math> K_{s} </math> = Interatomic bond stiffness | |||
Youngs Modulus = (<math> Y = K_{s}/d </math>) | |||
Youngs Modulus: <math> Y ={\frac{Stress}{Strain}}</math> | |||
<math> Stress = {\frac{F_{tension}}{Area_{Cross Sectional}}} </math> | |||
<math> Strain = {\frac{ΔL_{wire}}{L_{0}}} </math> | |||
===Speeds of Various Compositions=== | |||
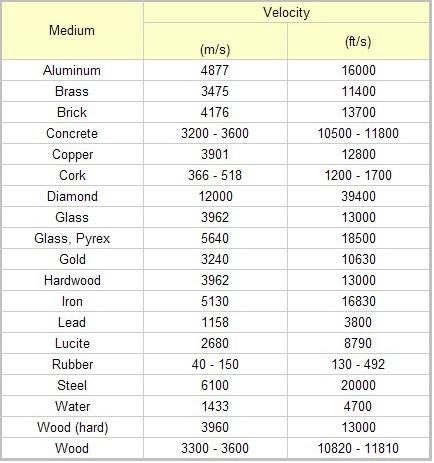
[[File:speedofsound.jpg]] | |||
==Examples== | |||
Be sure to show all steps in your solution and include diagrams whenever possible | Be sure to show all steps in your solution and include diagrams whenever possible | ||
===Theoretical=== | |||
Two metal rods are made of different elements. The interatomic spring stiffness of element A is four times larger than the interatomic spring stiffness for element B. The mass of an atom of element A is four times greater than the mass of an atom of element B. The atomic diameters are approximately the same for A and B. What is the ratio of the speed of sound in rod A to the speed of sound in rod B? | |||
Solution: In this situation, the ratio of the speed of sound in rod A to the speed of sound in rod B is 1. | |||
Looking at the formula for computing speed of sound in solids, <math> {V_{s}} = d* √ (K_{s}/m_{atom}) </math>, you see that velocity depends three factors, interatomic stiffness, the mass of one atom, and interatomic bond length. The two rods differences in atomic mass and interatomic stiffness offset each other when the equations are set equal, and the ratio is determined to be 1. | |||
History | |||
<math> d* √ 4(K_{s}/m_{atom}) = d* √ (K_{s}/4m_{atom}) </math> After simplification <math> V_{s_{1}} = V_{s{2}} </math> | |||
===Numerical Example 1=== | |||
A certain metal with atomic mass 2.7 × 10−25 kg has an interatomic bond with length 2.3 × 10−10 m and stiffness 46 N/m. What is the speed of sound in a rod made of this metal? | |||
Solution: | |||
===Numerical Example 2=== | |||
The Young's Modulus value of silver is 7.75e+10, atomic mass of silver is 108 g/mole, and the density of silver is 10.5 g/cm3. Using this information, calculate the speed of sound in silver. | |||
==Connectedness== | |||
The computation of speed of sound in solids is dependent on a mass' interatomic properties, such as interatomic bond length. I find it interesting when a object's interatomic properties determine its functionality on a larger scale. In the case of speed of sound in solids, the objects elasticity depends on the interatomic bond length. | |||
While the computation of speed of sound in solids may not seem related to Industrial Engineering, it has clear implications in the process of choosing building materials, which is a notable section of industrial engineering. For example, if you are planning to build something soundproof, it would be optimal to choose a solid with a very low speed of sound velocity. | |||
The industrial applications in terms of construction are vast. An objects ability to block/allow sound waves through it is very important. Of course, insulation materials and sound proof wall materials come to thought at first. However, in some cases, contractors need to build structures that allow sound to travel through, in which they would choose solid materials that correlate with high speeds of sound. | |||
==History== | |||
The speed of sound in air was first measured by Sir Isaac Newton, and first correctly computed by Pierre-Simon Laplace in 1816. Before this precise measurement, attempts had been made across Europe during the 1700s, most famously Reverend William Derham's experiment in 1709 across the town of Upminister, England. Reverend Derham used a shotgun's noise and several known landmarks around time to measure the time it took for the sound of the blast to be heard from select distances. | |||
Young's Modulus was named after English physicist Thomas Young. In actuality, the concept was developed earlier by physicists Leonhard Euler and Giordano Riccati in the 1720s. | |||
== See also == | |||
Youngs Modulus: [http://www.physicsbook.gatech.edu/Young%27s_Modulus] | |||
Interatomic Bonds: [http://www.physicsbook.gatech.edu/Length_and_Stiffness_of_an_Interatomic_Bond] | |||
===Further reading=== | |||
Further Information can be found on the speed of sound in solids in ''Matter and Interactions, 4th Edition'' by Ruth W. Chabay & Bruce A. Sherwood | |||
===External links=== | |||
Internet resources on this topic can be found at: | |||
Engineering Tool Box [http://www.engineeringtoolbox.com/sound-speed-solids-d_713.html] | |||
Hyperphysics [http://hyperphysics.phy-astr.gsu.edu/hbase/sound/souspe2.html] | |||
Potto Project [http://www.potto.org/gasDynamics/node73.html] | |||
NDT Resource Center [https://www.nde-ed.org/EducationResources/CommunityCollege/Ultrasonics/Physics/elasticsolids.htm] | |||
==References== | |||
This section contains the the references used while writing this page | |||
Chart from [http://www.rcgroups.com/forums/attachment.php?attachmentid=3397792] | |||
''Matter and Interactions 4th Edition'' by Chabay and Sherwood | |||
Category: Which Category did you place this in? | [[Category:Which Category did you place this in?]] | ||
Latest revision as of 16:37, 5 December 2015
This page discusses calculating the speed of sound in various solids and provides examples of such calculations. Claimed by Dpatel322 @ 12/1
The Main Idea
The speed of sound is the speed that sound wave travels through a particular medium. In comparison to air, sound travels considerably faster in solids. The speed that sound travels in various solids depends on the solid's density and elasticity, as these factors effect the ability of the sound waves vibrational energy to transfer across the solid medium.
A Mathematical Model
The speed of sound in solids [math]\displaystyle{ {V_{s}} }[/math] can be determined by the equation. Young's Modulus is a measure of elasticity of an object, and it can be computed to solve for interatomic values, such as interatomic bond stiffness or interatomic bond length.
[math]\displaystyle{ {V_{s}} = d* √ (K_{s}/m_{atom}) }[/math]
[math]\displaystyle{ d }[/math] = interatomic bond length
[math]\displaystyle{ K_{s} }[/math] = Interatomic bond stiffness
Youngs Modulus = ([math]\displaystyle{ Y = K_{s}/d }[/math])
Youngs Modulus: [math]\displaystyle{ Y ={\frac{Stress}{Strain}} }[/math]
[math]\displaystyle{ Stress = {\frac{F_{tension}}{Area_{Cross Sectional}}} }[/math]
[math]\displaystyle{ Strain = {\frac{ΔL_{wire}}{L_{0}}} }[/math]
Speeds of Various Compositions
Examples
Be sure to show all steps in your solution and include diagrams whenever possible
Theoretical
Two metal rods are made of different elements. The interatomic spring stiffness of element A is four times larger than the interatomic spring stiffness for element B. The mass of an atom of element A is four times greater than the mass of an atom of element B. The atomic diameters are approximately the same for A and B. What is the ratio of the speed of sound in rod A to the speed of sound in rod B?
Solution: In this situation, the ratio of the speed of sound in rod A to the speed of sound in rod B is 1.
Looking at the formula for computing speed of sound in solids, [math]\displaystyle{ {V_{s}} = d* √ (K_{s}/m_{atom}) }[/math], you see that velocity depends three factors, interatomic stiffness, the mass of one atom, and interatomic bond length. The two rods differences in atomic mass and interatomic stiffness offset each other when the equations are set equal, and the ratio is determined to be 1.
[math]\displaystyle{ d* √ 4(K_{s}/m_{atom}) = d* √ (K_{s}/4m_{atom}) }[/math] After simplification [math]\displaystyle{ V_{s_{1}} = V_{s{2}} }[/math]
Numerical Example 1
A certain metal with atomic mass 2.7 × 10−25 kg has an interatomic bond with length 2.3 × 10−10 m and stiffness 46 N/m. What is the speed of sound in a rod made of this metal?
Solution:
Numerical Example 2
The Young's Modulus value of silver is 7.75e+10, atomic mass of silver is 108 g/mole, and the density of silver is 10.5 g/cm3. Using this information, calculate the speed of sound in silver.
Connectedness
The computation of speed of sound in solids is dependent on a mass' interatomic properties, such as interatomic bond length. I find it interesting when a object's interatomic properties determine its functionality on a larger scale. In the case of speed of sound in solids, the objects elasticity depends on the interatomic bond length.
While the computation of speed of sound in solids may not seem related to Industrial Engineering, it has clear implications in the process of choosing building materials, which is a notable section of industrial engineering. For example, if you are planning to build something soundproof, it would be optimal to choose a solid with a very low speed of sound velocity.
The industrial applications in terms of construction are vast. An objects ability to block/allow sound waves through it is very important. Of course, insulation materials and sound proof wall materials come to thought at first. However, in some cases, contractors need to build structures that allow sound to travel through, in which they would choose solid materials that correlate with high speeds of sound.
History
The speed of sound in air was first measured by Sir Isaac Newton, and first correctly computed by Pierre-Simon Laplace in 1816. Before this precise measurement, attempts had been made across Europe during the 1700s, most famously Reverend William Derham's experiment in 1709 across the town of Upminister, England. Reverend Derham used a shotgun's noise and several known landmarks around time to measure the time it took for the sound of the blast to be heard from select distances.
Young's Modulus was named after English physicist Thomas Young. In actuality, the concept was developed earlier by physicists Leonhard Euler and Giordano Riccati in the 1720s.
See also
Youngs Modulus: [1] Interatomic Bonds: [2]
Further reading
Further Information can be found on the speed of sound in solids in Matter and Interactions, 4th Edition by Ruth W. Chabay & Bruce A. Sherwood
External links
Internet resources on this topic can be found at:
Engineering Tool Box [3]
Hyperphysics [4]
Potto Project [5]
NDT Resource Center [6]
References
This section contains the the references used while writing this page
Chart from [7]
Matter and Interactions 4th Edition by Chabay and Sherwood