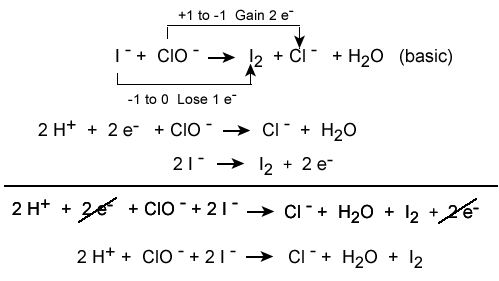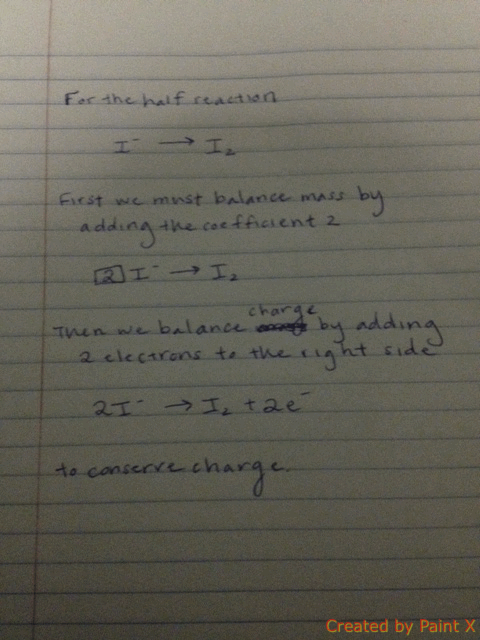Conservation of Charge: Difference between revisions
No edit summary |
|||
| (4 intermediate revisions by the same user not shown) | |||
| Line 83: | Line 83: | ||
Franklin, Benjamin (1769). ''Experiments And Observations On Electricity, Made At Philadelphia in America''. London. | Franklin, Benjamin (1769). ''Experiments And Observations On Electricity, Made At Philadelphia in America''. London. | ||
== | ==References== | ||
1. http://www.britannica.com/science/charge-conservation | |||
2. https://en.wikipedia.org/wiki/Charge_conservation | |||
3. http://farside.ph.utexas.edu/teaching/302l/lectures/node12.html | |||
4. http://people.physics.tamu.edu/saslow/chap_02all.pdf | |||
Images: | |||
http://www.electronspin.org/11.htm | |||
http://crescentok.com/staff/jaskew/isr/tigerchem/redox/redox9.htm | |||
http://www.askiitians.com/iit-jee-radioactive-decay-of-substances/radioactivity/ | |||
[[Category: | [[Category:Interactions]] | ||
Latest revision as of 20:25, 5 December 2015
oduan3
Conservation of charge is the principle that the sum of the electrical charge of a closed system is constant.
The Main Idea
The idea that the net charge of a closed system is constant implies that: if a charge appears in a previously neutral system, an equal and opposite charge appears in another part of the system. Individual charges, however, can be created or destroyed. The sum of all electrical charge in the universe, then, is assumed to be some constant quantity (presumably zero, although this is not certain).[1]
A Mathematical Model
Given the intial and final times (Ti and Tf), the charge of a system can be described using the equation Q(Tf) = Q(Ti) + Qin - Qout. This allows us to predict the charge of a system after a given time has passed by adding the total flow of charge into the system and subtracting the total flow of charge out of the system.
Furthermore, conservation of charge is described by one of Maxwell's equations
which states that the divergence of current density (J) is proportional to the change in charge density (rho).[2]
Examples
Simple
A system contains three particles: particle 1 has a charge of 2Q, particle 2 has a charge of -2Q, and particle 3 has a charge of 3Q. What is the net charge on the system?
Solution:
Add the charges together to get the net charge.
-2 + 2 + 3 = 3 Q
Middling
A system contains two spheres of the same mass. Sphere 1 has a charge of -1C and Sphere 2 has a charge of + 5C. The two spheres are brought together, touch, and are separated again. What is the net charge on each of the two spheres?
Solution:
Since the two spheres have the same mass, the charge will distribute itself evenly between the two spheres. Add the two charges, then divide by 2.
(-1+5)/2 = 3 C
Difficult
Thorium-234 (which is electrically neutral) decays by emitting a beta particle (charge of -1). What is the atomic number after the decay, given that the new atom is electrically neutral? (hint: the atomic number of thorium is 90)
Solution:
An electrically neutral atom contains equal numbers of electrons and protons. Thorium has an atomic number of 90, which means it has 90 protons and 90 electrons. After considering conservation of charge, we know that the new particle created must have an atomic number of 91 if it is to stay electrically neutral, as the diagram demonstrates.
Connectedness
Analyzing and predicting the outcome of nuclear reactions depends on the conservation of charge. For example, a neutron decays into a proton, an electron, and an antineutrino, thus conserving the overall neutral charge before and after the reaction.
Conservation of charge is also relevant to chemistry, especially for predicting the outcome of reactions (redox reactions in particular). For example, the typical sodium and chlorine ions have equal and opposite charges, and when they react, they form a neutral compound via the transfer of one electron to another, which abides by the conservation of charge rule (-1 + 1 = 0). The process of balancing chemical equations requires that the net charge on each side of the equation be equal, so electrons are "added" to each side as necessary to balance out the charges.
Balancing each half-reaction requires knowledge of conservation of mass and conservation of charge, as demonstrated below.
An industrial application of conservation of charge is the construction of electrical circuits. Analyzing the key components of a circuit (such as resistors, switches, and batteries) and the flow of electricity through wires requires a fundamental understanding of Kirchhoff's rules. One of Kirchhoff's rules, commonly known as the junction rule, states that the total amount of current flowing into a junction is equivalent to the amount of current flowing out of a junction. Since current is a measure of the amount of charge per unit time, the junction rule comes as a direct consequence of the law of conservation of charge.
History
Ancient Greeks as early as 1000 BC observed that small bits of chaff stuck to amber jewelry after it was polished. The act of polishing amber left an excess of negative electrons on the amber, polarizing neutral particles and causing them to become electrically attracted to the amber. William Gilbert documented the effect in 1600 as the "amber effect" in his book On Magnetism. The principle was officially discovered by Benjamin Franklin In the 18th century. He described electrical charge as a "fluid"; an object with an excess of fluid had one charge, and an object deficient in fluid had an opposite charge (the beginnings of the idea of positive and negative charges), demonstrating this phenomena via what is now known as static electricity. In the experiment, a glass rod is rubbed against cloth, giving the glass rod a net positive charge. One person, standing on an insulator, takes the rod and touches another person, giving the other person a positive charge by means of electrical induction. Another person, standing on the floor, experiences a charge, indicating a net movement of charge between the three people in an "isolated" system, where charge is not created. [3] [4]
See also
Further reading
Franklin, Benjamin (1769). Experiments And Observations On Electricity, Made At Philadelphia in America. London.
References
1. http://www.britannica.com/science/charge-conservation
2. https://en.wikipedia.org/wiki/Charge_conservation
3. http://farside.ph.utexas.edu/teaching/302l/lectures/node12.html
4. http://people.physics.tamu.edu/saslow/chap_02all.pdf
Images:
http://www.electronspin.org/11.htm
http://crescentok.com/staff/jaskew/isr/tigerchem/redox/redox9.htm
http://www.askiitians.com/iit-jee-radioactive-decay-of-substances/radioactivity/