Standing waves: Difference between revisions
Anvikshabusa (talk | contribs) |
Anvikshabusa (talk | contribs) No edit summary |
||
| (24 intermediate revisions by the same user not shown) | |||
| Line 3: | Line 3: | ||
[[File:Resultant_Standing_Wave.png|400px|thumb|right|Standing Wave as a result of wave interference.]] | [[File:Resultant_Standing_Wave.png|400px|thumb|right|Standing Wave as a result of wave interference.]] | ||
The | The vibration associated with resonance in objects like strings and air columns have characteristic patterns called '''Standing waves'''. These standing waves arise from the combination of reflection and interference such that the reflected waves interfere constructively with the incident waves. An important part of this constructive interference is the fact that the waves change phase upon reflection from a fixed end. Under these conditions, the medium appears to vibrate in segments or regions and the fact that these vibrations are made up of traveling waves is not apparent - hence the term "standing wave". | ||
The behavior of the waves at the points of minimum and maximum vibrations (nodes and antinodes) contributes to the constructive interference which forms the resonant standing waves. | The behavior of the waves at the points of minimum and maximum vibrations (nodes and antinodes) contributes to the constructive interference which forms the resonant standing waves. Standing waves occur in transverse waves, but also occur with the longitudinal waves in an air column. Standing waves in air columns also form nodes and antinodes, but the phase changes involved must be separately examined for air columns. | ||
==Nodes and Antinodes== | ==Nodes and Antinodes== | ||
| Line 66: | Line 56: | ||
As one studies harmonics and their standing wave patterns, it becomes evident that there is a predictability about them. Not surprisingly, this predictability expresses itself in a series of mathematical relationships that relate the wavelength of the wave pattern to the length of the medium. Additionally, the frequency of each harmonic is mathematically related to the frequency of the first harmonic. Each consecutive harmonic is characterized by having one additional node and antinode compared to the previous one | As one studies harmonics and their standing wave patterns, it becomes evident that there is a predictability about them. Not surprisingly, this predictability expresses itself in a series of mathematical relationships that relate the wavelength of the wave pattern to the length of the medium. Additionally, the frequency of each harmonic is mathematically related to the frequency of the first harmonic. Each consecutive harmonic is characterized by having one additional node and antinode compared to the previous one | ||
==Mathematical model: Standing waves at different harmonics== | |||
In one dimension, two waves with the same frequency, wavelength and amplitude traveling in opposite directions will interfere and produce a standing wave or stationary wave. For example: a wave traveling to the right along a taut string and hitting the end will reflect back in the other direction along the string, and the two waves will superpose to produce a standing wave. The reflective wave has to have the same amplitude and frequency as the incoming wave. | |||
If the string is held at both ends, forcing zero movement at the ends, the ends become nodes. The length of the string then becomes a measure of which waves the string will entertain: the longest wavelength is called the '''Fundamental frequency'''. Half a wavelength of the fundamental fits on the string. Shorter wavelengths also can be supported as long as multiples of half a wavelength fit on the string. The frequencies of these waves all are multiples of the fundamental, and are called '''Harmonic''' or overtone. | |||
Harmonic waves travelling in opposite directions can be represented by the equations below: | |||
:<math> | |||
y_1\; =\; y_0\, \sin(kx - \omega t)\, | |||
</math> | |||
= | and | ||
:<math> | |||
y_2\; =\; y_0\, \sin(kx +\omega t)\, | |||
</math> | |||
where: | |||
*''y<sub>0</sub>'' is the ''amplitude'' of the wave, | |||
*''ω'' (called ''angular frequency'', measured in ''radians per second'') is ''2π'' times the frequency (in ''hertz''), | |||
*''k'' (called the ''wave number'' and measured in ''radians per metre'') is ''2π'' divided by the wavelength ''λ'' (in ''metres''), and | |||
*''x'' and ''t'' are variables for longitudinal position and time, respectively. | |||
So the resultant wave ''y'' equation will be the sum of ''y<sub>1</sub>'' and ''y<sub>2</sub>'': | |||
:<math> | |||
y\; =\; y_0\, \sin(kx - \omega t)\; +\; y_0\, \sin(kx + \omega t).\, | |||
</math> | |||
Using the Trigonometric identity#Product-to-sum and sum-to-product identities|trigonometric sum-to-product identity for 'sin(''u'') + sin(''v'')' to simplify: | |||
:<math> | |||
y\; =\; 2\, y_0\, \cos(\omega t)\; \sin(kx).\, | |||
</math> | |||
== | This describes a wave that oscillates in time, but has a spatial dependence that is stationary: sin(''kx''). At locations ''x'' = 0, ''λ''/2, ''λ'', 3''λ''/2, ... (the nodes) the amplitude is always zero, whereas at locations ''x'' = ''λ''/4, 3''λ''/4, 5''λ''/4, ... called the anti-nodes, the amplitude is maximum. The distance between two conjugative nodes or anti-nodes is ''λ''/2. | ||
===A Computational Model=== | |||
Click on the following link to understand standing waves better: | |||
[https://trinket.io/embed/glowscript/759832b92d Demo program on Standing Waves] | |||
==Application== | ==Application== | ||
| Line 102: | Line 114: | ||
-When you tune in a radio station, you are making the antenna circuit resonate with a particular carrier wave. The radio wave induces a standing wave of alternating current in the antenna circuit. | -When you tune in a radio station, you are making the antenna circuit resonate with a particular carrier wave. The radio wave induces a standing wave of alternating current in the antenna circuit. | ||
== See also == | |||
[[Mechanical waves]] | |||
[[Transverse and longitudinal waves]] | |||
[[interference]] | |||
[[Gravitational waves]] | |||
===Further reading=== | ===Further reading=== | ||
Tsokos, K. A. Physics for the IB Diploma. Cambridge: Cambridge UP, 2010. Print. | |||
Georgi, Howard. The Physics of Waves. Englewood Cliffs, NJ: Prentice Hall, 1993. Print. | |||
6, 1. Of, Stanford Physics Dept., Standing Waves On A String, and P28 Lab 6. Standing Waves on a String (n.d.): n. pag. Web. | |||
== | ===External links=== | ||
https://en.wikipedia.org/wiki/Standing_wave | https://en.wikipedia.org/wiki/Standing_wave | ||
http://hyperphysics.phy-astr.gsu.edu/hbase/waves/standw.html#c4 | http://hyperphysics.phy-astr.gsu.edu/hbase/waves/standw.html#c4 | ||
http://hyperphysics.phy-astr.gsu.edu/hbase/waves/funhar.html#c3 | http://hyperphysics.phy-astr.gsu.edu/hbase/waves/funhar.html#c3 | ||
==References== | |||
"What Are Some Examples of Stationary Waves in Real Life?" - Quora. N.p., n.d. Web. 05 Dec. 2015. | |||
"Harmonics and Patterns." Harmonics and Patterns. N.p., n.d. Web. 05 Dec. 2015. | |||
"Standing Wave Patterns." Standing Wave Patterns. N.p., n.d. Web. 05 Dec. 2015. | |||
"Characteristics of Stationary Waves." Characteristics of Stationary Waves. N.p., n.d. Web. 05 Dec. 2015. | |||
"Standing Waves." Standing Waves. N.p., n.d. Web. 05 Dec. 2015. | |||
"Fundamental and Harmonics." Fundamental and Harmonic Resonances. N.p., n.d. Web. 05 Dec. 2015. | |||
[[Category: Waves]] | [[Category: Waves]] | ||
Latest revision as of 20:15, 5 December 2015
Claimed by Anviksha Busa
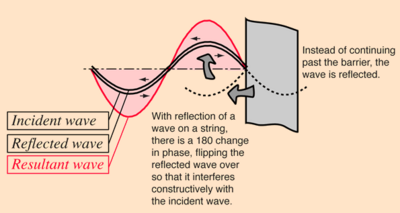
The vibration associated with resonance in objects like strings and air columns have characteristic patterns called Standing waves. These standing waves arise from the combination of reflection and interference such that the reflected waves interfere constructively with the incident waves. An important part of this constructive interference is the fact that the waves change phase upon reflection from a fixed end. Under these conditions, the medium appears to vibrate in segments or regions and the fact that these vibrations are made up of traveling waves is not apparent - hence the term "standing wave".
The behavior of the waves at the points of minimum and maximum vibrations (nodes and antinodes) contributes to the constructive interference which forms the resonant standing waves. Standing waves occur in transverse waves, but also occur with the longitudinal waves in an air column. Standing waves in air columns also form nodes and antinodes, but the phase changes involved must be separately examined for air columns.
Nodes and Antinodes
Standing waves on a string are a result of traveling waves interfering both destructively and constructively. The nodes (places of zero amplitude) are due to destructive interference, and the antinodes (places of maximum amplitude) are due to constructive interference. When a standing wave appears, the nodes and antinodes are fixed in place. When the conditions of the tension in the string, the linear density and the frequency of oscillations are just right, standing waves appear.
-
Standing wave in stationary medium. The red dots represent the wave .
-
A standing wave (black) depicted as the sum of two propagating waves traveling in opposite directions (red and blue).
There are a variety of patterns by strings could naturally vibrate. Each pattern is associated with one its natural frequencies. Each standing wave pattern is referred to as a harmonic. There are a variety of other low energy vibrational patterns that could be established by some basic traits:
1. There is an alternating pattern of nodes and antinodes.
2. There are either a half-number or a whole number of waves within the pattern established on the string.
3. Nodal positions (points of no displacement) are established at the ends of the string where the string is clamped down in a fixed position.
4. One pattern is related to the next pattern by the addition (or subtraction) of one or more nodes (and antinodes).
Standing Wave Patterns
First Harmonic
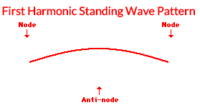
The simplest standing wave pattern has points of no displacement (nodes) at the two ends and one point of maximum displacement (antinode) in the middle. This is the first harmonic. It is the simplest wave pattern produced and is obtained when the teacher introduced vibrations into the end of the medium at low frequencies.
Second Harmonic
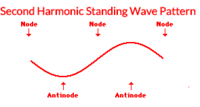
Other wave patterns can be observed when it is vibrated at greater frequencies. For instance, if the teacher vibrates the end with twice the frequency as that associated with the first harmonic, then a second standing wave pattern can be achieved. This standing wave pattern is characterized by nodes on the two ends and an additional node in the exact center. As in all standing wave patterns, every node is separated by an antinode. This pattern with three nodes and two antinodes is referred to as the second harmonic.
Third Harmonic
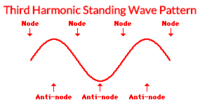
If the frequency is increased even more, then the third harmonic wave pattern can be produced. The standing wave pattern for the third harmonic has an additional node and antinode between its ends.
Other Harmonics
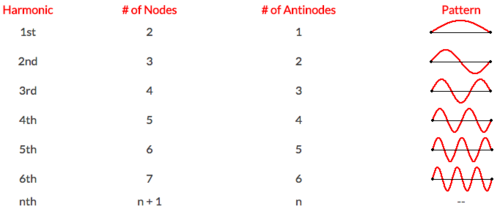
As one studies harmonics and their standing wave patterns, it becomes evident that there is a predictability about them. Not surprisingly, this predictability expresses itself in a series of mathematical relationships that relate the wavelength of the wave pattern to the length of the medium. Additionally, the frequency of each harmonic is mathematically related to the frequency of the first harmonic. Each consecutive harmonic is characterized by having one additional node and antinode compared to the previous one
Mathematical model: Standing waves at different harmonics
In one dimension, two waves with the same frequency, wavelength and amplitude traveling in opposite directions will interfere and produce a standing wave or stationary wave. For example: a wave traveling to the right along a taut string and hitting the end will reflect back in the other direction along the string, and the two waves will superpose to produce a standing wave. The reflective wave has to have the same amplitude and frequency as the incoming wave.
If the string is held at both ends, forcing zero movement at the ends, the ends become nodes. The length of the string then becomes a measure of which waves the string will entertain: the longest wavelength is called the Fundamental frequency. Half a wavelength of the fundamental fits on the string. Shorter wavelengths also can be supported as long as multiples of half a wavelength fit on the string. The frequencies of these waves all are multiples of the fundamental, and are called Harmonic or overtone.
Harmonic waves travelling in opposite directions can be represented by the equations below:
- [math]\displaystyle{ y_1\; =\; y_0\, \sin(kx - \omega t)\, }[/math]
and
- [math]\displaystyle{ y_2\; =\; y_0\, \sin(kx +\omega t)\, }[/math]
where:
- y0 is the amplitude of the wave,
- ω (called angular frequency, measured in radians per second) is 2π times the frequency (in hertz),
- k (called the wave number and measured in radians per metre) is 2π divided by the wavelength λ (in metres), and
- x and t are variables for longitudinal position and time, respectively.
So the resultant wave y equation will be the sum of y1 and y2:
- [math]\displaystyle{ y\; =\; y_0\, \sin(kx - \omega t)\; +\; y_0\, \sin(kx + \omega t).\, }[/math]
Using the Trigonometric identity#Product-to-sum and sum-to-product identities|trigonometric sum-to-product identity for 'sin(u) + sin(v)' to simplify:
- [math]\displaystyle{ y\; =\; 2\, y_0\, \cos(\omega t)\; \sin(kx).\, }[/math]
This describes a wave that oscillates in time, but has a spatial dependence that is stationary: sin(kx). At locations x = 0, λ/2, λ, 3λ/2, ... (the nodes) the amplitude is always zero, whereas at locations x = λ/4, 3λ/4, 5λ/4, ... called the anti-nodes, the amplitude is maximum. The distance between two conjugative nodes or anti-nodes is λ/2.
A Computational Model
Click on the following link to understand standing waves better:
Demo program on Standing Waves
Application
Standing waves are used and seen in multiple real life examples. It is a major contributor in quantum mechanics. It can also be found in the following:
-In string instruments, a plucked or bowed string makes the note is does because only certain frequencies of stationary (or "standing") waves are able to form on that string under those conditions (e.g., a finger holding down the string at a certain position). Any vibrations that aren't at the right frequencies to make standing waves quickly cancel themselves out, and so it's the standing wave frequencies that we actually hear.
-Similarly, for woodwind instruments, we get the notes we get because of what standing waves are able to form within the tube of air inside the instrument. (Strings and woodwinds sound different from one another because they allow different combinations of overtones (higher-frequency standing waves) to form.)
-Waves on the beach
-When you tune in a radio station, you are making the antenna circuit resonate with a particular carrier wave. The radio wave induces a standing wave of alternating current in the antenna circuit.
See also
Transverse and longitudinal waves
Further reading
Tsokos, K. A. Physics for the IB Diploma. Cambridge: Cambridge UP, 2010. Print.
Georgi, Howard. The Physics of Waves. Englewood Cliffs, NJ: Prentice Hall, 1993. Print.
6, 1. Of, Stanford Physics Dept., Standing Waves On A String, and P28 Lab 6. Standing Waves on a String (n.d.): n. pag. Web.
External links
https://en.wikipedia.org/wiki/Standing_wave
http://hyperphysics.phy-astr.gsu.edu/hbase/waves/standw.html#c4
http://hyperphysics.phy-astr.gsu.edu/hbase/waves/funhar.html#c3
References
"What Are Some Examples of Stationary Waves in Real Life?" - Quora. N.p., n.d. Web. 05 Dec. 2015.
"Harmonics and Patterns." Harmonics and Patterns. N.p., n.d. Web. 05 Dec. 2015.
"Standing Wave Patterns." Standing Wave Patterns. N.p., n.d. Web. 05 Dec. 2015.
"Characteristics of Stationary Waves." Characteristics of Stationary Waves. N.p., n.d. Web. 05 Dec. 2015.
"Standing Waves." Standing Waves. N.p., n.d. Web. 05 Dec. 2015.
"Fundamental and Harmonics." Fundamental and Harmonic Resonances. N.p., n.d. Web. 05 Dec. 2015.