Magnus Effect: Difference between revisions
No edit summary |
|||
| (35 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
The '''Magnus effect''' is the effect in which one can observe a ball or cylinder curving from its initial path of motion | The '''Magnus effect''' is the effect in which one can observe a ball or cylinder curving through the air from its initial path of motion. | ||
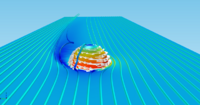
[[File:Magnus effect - slider.png|200px|thumb|left|The result of the Magnus effect on a rotating ball]] | |||
Contents | Contents | ||
1 The Magnus Effect | |||
1.1 A Mathematical Model | 1.1 A Mathematical Model | ||
1.2 A Computational Model | 1.2 A Computational Model | ||
2 | 2 Connectedness | ||
3 History | |||
4 See also | |||
4.1 Further reading | |||
3 | 4.2 External links | ||
4 | 5 References | ||
== The Magnus Effect == | == The Magnus Effect == | ||
The '''Magnus Effect''' is the lift force created on a rotating spherical or cylindrical object about an axis as it moves through a fluid. The force is perpendicular to the forward motion and causes the object to deviate from its standard flight path. | The '''Magnus Effect''' is the lift force created on a rotating spherical or cylindrical object about an axis as it moves through a fluid. The force is perpendicular to the forward motion and causes the object to deviate from its standard flight path. Areas of high and low pressure are formed around the object, and the object tends to curve toward low pressure. | ||
''Picture:'' The result of the Magnus effect on a rotating ball [https://ellieslicesbagels.files.wordpress.com/2014/05/curveball.jpg] | |||
== A Mathematical Model == | == A Mathematical Model == | ||
The Magnus effect is an application of Bernoulli's theorem. This theorem states that if a fluid has velocity v, the pressure p of that fluid is equal to 1rv^2, with r being the constant fluid density. Since the pressure is normal to the surface of an object, the upward component is -sin(q)p(q). If we integrate the pressure times the surface area of a cylinder with radius r, we get the lift: | The Magnus effect is an application of Bernoulli's theorem. This theorem states that if a fluid has velocity v, the pressure p of that fluid is equal to 1rv^2, with r being the constant fluid density. Since the pressure is normal to the surface of an object, the upward component is -sin(q)p(q). If we integrate the pressure times the surface area of a cylinder with radius r, we get the lift: | ||
| Line 41: | Line 46: | ||
== A Computational Model == | == A Computational Model == | ||
A computational model of the Magnus effect can be observed by this graphic created in VPython: | |||
Magnus effect [https://www.youtube.com/watch?v=NpzKn8INm2o] | |||
== Connectedness == | |||
The Magnus effect can be seen perhaps most commonly in the world of sports. In baseball, pitchers vary their grip, release, and pressure placed on each finger in an effort to maximize the Magnus effect and achieve large levels of break on their pitches. | |||
''Picture:'' The forces on a curveball, including Magnus force [https://i.ytimg.com/vi/Fyh5XTpTzmI/maxresdefault.jpg] | |||
A breakdown of the Magnus effect on pitches can be seen in this video showing the cutter of legendary Yankees closer Mariano Rivera [https://www.youtube.com/watch?v=zH_wEUBWp9k] | |||
== History == | |||
Sir Isaac Newton recorded the effects in 1672 after observing the flight of tennis balls at his college in Cambridge. Benjamin Robins also described what would come to be known as the Magnus effect in 1742 after observing the curving of musket balls. However, the effect would be named after German physicist and chemist Gustav Magnus (1802-1870). He experimented with rotating spheres and cylinders to study their aerodynamics. | |||
== See also == | |||
'''Further reading''' | |||
For more on the Magnus effect and other physics in baseball, see | |||
"The Physics of Baseball"[http://baseball.physics.illinois.edu/Adair_PhysicsToday_May95.pdf] | |||
"The effect of spin on the flight of a baseball"[http://scitation.aip.org/content/aapt/journal/ajp/76/2/10.1119/1.2805242] | |||
'''External links''' | |||
A physics resource written by experts for an expert audience Physics Portal[https://en.wikipedia.org/wiki/Portal:Physics] | |||
A wiki book on modern physics Modern Physics Wiki[https://en.wikibooks.org/wiki/Modern_Physics] | |||
The MIT open courseware for intro physics MITOCW Wiki[http://ocw.mit.edu/resources/res-8-002-a-wikitextbook-for-introductory-mechanics-fall-2009/index.htm] | |||
- | An online concept map of intro physics HyperPhysics[http://hyperphysics.phy-astr.gsu.edu/hbase/hph.html] | ||
Interactive physics simulations PhET[https://phet.colorado.edu/en/simulations/category/physics] | |||
OpenStax algebra based intro physics textbook College Physics[https://openstaxcollege.org/textbooks/college-physics] | |||
The Open Source Physics project is a collection of online physics resources OSP[http://www.opensourcephysics.org/] | |||
A resource guide compiled by the AAPT[http://www.aapt.org/] for educators ComPADRE[http://www.compadre.org/] | |||
== References == | |||
http://www.mathpages.com/home/kmath258/kmath258.htm[http://www.mathpages.com/home/kmath258/kmath258.htm] | |||
[ | http://everything.explained.today/Magnus_effect/[http://everything.explained.today/Magnus_effect/] | ||
http://baseball.physics.illinois.edu/Adair_PhysicsToday_May95.pdf[http://baseball.physics.illinois.edu/Adair_PhysicsToday_May95.pdf] | |||
http://scitation.aip.org/content/aapt/journal/ajp/76/2/10.1119/1.2805242[http://scitation.aip.org/content/aapt/journal/ajp/76/2/10.1119/1.2805242] | |||
Category: Interactions [http://www.physicsbook.gatech.edu/Main_Page] | |||
Latest revision as of 05:10, 6 December 2015
The Magnus effect is the effect in which one can observe a ball or cylinder curving through the air from its initial path of motion.
Contents
1 The Magnus Effect
1.1 A Mathematical Model
1.2 A Computational Model
2 Connectedness
3 History
4 See also
4.1 Further reading
4.2 External links
5 References
The Magnus Effect
The Magnus Effect is the lift force created on a rotating spherical or cylindrical object about an axis as it moves through a fluid. The force is perpendicular to the forward motion and causes the object to deviate from its standard flight path. Areas of high and low pressure are formed around the object, and the object tends to curve toward low pressure.
Picture: The result of the Magnus effect on a rotating ball [1]
A Mathematical Model
The Magnus effect is an application of Bernoulli's theorem. This theorem states that if a fluid has velocity v, the pressure p of that fluid is equal to 1rv^2, with r being the constant fluid density. Since the pressure is normal to the surface of an object, the upward component is -sin(q)p(q). If we integrate the pressure times the surface area of a cylinder with radius r, we get the lift:
F_p = -(rho*Gamma)/4 (1+1/r^2)
If we say r = 1, the net lift can be shown as:
L = -rho*v_0*Gamma
This is the Magnus effect.
A Computational Model
A computational model of the Magnus effect can be observed by this graphic created in VPython: Magnus effect [2]
Connectedness
The Magnus effect can be seen perhaps most commonly in the world of sports. In baseball, pitchers vary their grip, release, and pressure placed on each finger in an effort to maximize the Magnus effect and achieve large levels of break on their pitches.
Picture: The forces on a curveball, including Magnus force [3]
A breakdown of the Magnus effect on pitches can be seen in this video showing the cutter of legendary Yankees closer Mariano Rivera [4]
History
Sir Isaac Newton recorded the effects in 1672 after observing the flight of tennis balls at his college in Cambridge. Benjamin Robins also described what would come to be known as the Magnus effect in 1742 after observing the curving of musket balls. However, the effect would be named after German physicist and chemist Gustav Magnus (1802-1870). He experimented with rotating spheres and cylinders to study their aerodynamics.
See also
Further reading
For more on the Magnus effect and other physics in baseball, see
"The Physics of Baseball"[5]
"The effect of spin on the flight of a baseball"[6]
External links
A physics resource written by experts for an expert audience Physics Portal[7]
A wiki book on modern physics Modern Physics Wiki[8]
The MIT open courseware for intro physics MITOCW Wiki[9]
An online concept map of intro physics HyperPhysics[10]
Interactive physics simulations PhET[11]
OpenStax algebra based intro physics textbook College Physics[12]
The Open Source Physics project is a collection of online physics resources OSP[13]
A resource guide compiled by the AAPT[14] for educators ComPADRE[15]
References
http://www.mathpages.com/home/kmath258/kmath258.htm[16]
http://everything.explained.today/Magnus_effect/[17]
http://baseball.physics.illinois.edu/Adair_PhysicsToday_May95.pdf[18]
http://scitation.aip.org/content/aapt/journal/ajp/76/2/10.1119/1.2805242[19]
Category: Interactions [20]