Using Capacitors to Measure Fluid Level: Difference between revisions
m (I realized I messed up the direction of the electric field in the model. Fixed it.) |
|||
| (13 intermediate revisions by the same user not shown) | |||
| Line 2: | Line 2: | ||
== | ==Structure of a Capacitor== | ||
<small>For more details, see [[capacitor]].</small> | <small>For more details, see [[capacitor]].</small> | ||
| Line 11: | Line 10: | ||
The magnitude of the electric field within a capacitor is <math>\left| \vec{E}_{capacitor} \right| = \frac{Q/A}{\epsilon_{0}}</math>, where the gap is only occupied by free space. <math>Q</math> is the charge on a plate and <math>A</math> is the area of a plate. Additionally, <math>\epsilon_{0}</math> is the permittivity of free space as detailed [[Constants|here]]. | The magnitude of the electric field within a capacitor is <math>\left| \vec{E}_{capacitor} \right| = \frac{Q/A}{\epsilon_{0}}</math>, where the gap is only occupied by free space. <math>Q</math> is the charge on a plate and <math>A</math> is the area of a plate. Additionally, <math>\epsilon_{0}</math> is the permittivity of free space as detailed [[Constants|here]]. | ||
==Relating Capacitance to Fluid Level== | |||
With a dielectric involved, we apply the equation <math>\vec{E}_{dielectric} = \frac{\vec{E}_{applied}}{K}</math>, where <math>K</math> is the dielectric constant of the material, and get <math>\left| \vec{E}_{dielectric} \right| = \frac{Q/A}{K\epsilon_{0}}</math>. The capacitance, <math>C=\frac{Q}{V}</math> (where <math>V</math> is the voltage) or <math>C=\frac{\epsilon_0 A K}{d}</math>, therefore changes with a varying dielectric constant. | With a dielectric involved, we apply the equation <math>\vec{E}_{dielectric} = \frac{\vec{E}_{applied}}{K}</math>, where <math>K</math> is the dielectric constant of the material, and get <math>\left| \vec{E}_{dielectric} \right| = \frac{Q/A}{K\epsilon_{0}}</math>. The capacitance, <math>C=\frac{Q}{V}</math> (where <math>V</math> is the voltage) or <math>C=\frac{\epsilon_0 A K}{d}</math>, therefore changes with a varying dielectric constant. | ||
When multiple materials are between the gap, for instance water and air, the overall capacitance would be <math>C=\epsilon_0 A (d_{water}+d_{air})(\frac{K_{water}}{d_{water}}+\frac{K_{air}}{d_{air}})</math>, where <math>d=d_{water}+d_{air}</math> and <math>K_{air} \approx 1</math>. Thus, correlating capacitance to known levels of water results in a calibration for a sensor using this technique, and the amount of water can be back calculated from the overall capacitance. With more than two dielectrics, the equation can be expanded to include these materials. | When multiple materials are between the gap, for instance water and air, the overall capacitance would be <math>C=\epsilon_0 A (d_{water}+d_{air})(\frac{K_{water}}{d_{water}}+\frac{K_{air}}{d_{air}})</math>, where <math>d=d_{water}+d_{air}</math> and <math>K_{air} \approx 1</math>. Thus, correlating capacitance to known levels of water results in a calibration for a sensor using this technique, and the amount of water can be back calculated from the overall capacitance. With more than two dielectrics, the equation can be expanded to include these materials. | ||
| Line 19: | Line 18: | ||
[[File:EFieldCapacitor.gif|thumb|A Python simulation depicting how varying the amount of dielectric within the gap of a capacitor (with two oppositely charged conducting plates) changes the corresponding electric field between the gap. Notice how more of a dielectric with a high dielectric constant reduces the electric field, which in turn increases the capacitance. ]] | [[File:EFieldCapacitor.gif|thumb|A Python simulation depicting how varying the amount of dielectric within the gap of a capacitor (with two oppositely charged conducting plates) changes the corresponding electric field between the gap. Notice how more of a dielectric with a high dielectric constant reduces the electric field, which in turn increases the capacitance. ]] | ||
For a simple simulation depicting how changing the amount of dielectric within the gap of a capacitor changes the corresponding electric field, please check out the [https://trinket.io | For a simple simulation depicting how changing the amount of dielectric within the gap of a capacitor changes the corresponding electric field, please check out the [https://trinket.io/glowscript/f10a10930e VPython simulation]. The charge on the capacitor as well as the dielectric constants for both dielectrics can be adjusted to visualize how the changes affect the electric field. Notice that the scale factor for the electric field is computed in such a way that the maximum length of the arrow is always the distance between the two plates, so adjusting constants proportionally may result in similar looking arrows (although the electric field will be different). Additionally, you can try changing the color on one of the dielectrics to better visualize the allocation of both within the gap of the capacitor. | ||
A decrease in electric field yields an increase in capacitance, so we can imagine how these two are related. With water | A decrease in electric field yields an increase in capacitance, so we can imagine how these two are related. With water and air surrounded by plastic, determining the water level is as simple as measuring the capacitance and solving for the amount of water. In practical applications, these sensors would have to be calibrated and an additional temperature sensor would be needed, because the dielectric constant changes with temperature. | ||
==Examples== | ==Examples== | ||
For an example, I will extract the scenario from a YouTube video [https://www.youtube.com/watch?v=nO_GJJ6HfTI here]. We want to build a capacitor and measure the capacitance with varying dielectric content. Using simple materials like aluminum foil, some sort of insulating material (like "Press n Seal" plastic) to insulate the capacitor from the water, and a device capable of measuring capacitance, we can see that capacitance varies with water level and a correlation for a constant temperature can be developed. | |||
==Connectedness== | ==Connectedness== | ||
===Connection to Personal Interest: Water Level Sensing=== | |||
<i>How is this topic connected to something that you are interested in?</i> <br> | |||
My father owns horses and in order to make sure they have water, he needed to walk far to check the troughs containing water. Instead, with assistance of videos [https://www.youtube.com/watch?v=Rd35tZZQL2o part I] and [https://www.youtube.com/watch?v=rH8x2E_lbng part II] (although these sensors work off of resistance, the data transferring portion really helped), we were able to construct a capacitative water level sensor that transmitted the information to us in the house, without requiring long treks to monitor the water. Thus, the interest stemmed from a determination to do less work. | |||
== | ===Connection to Major: Engineering Applications=== | ||
<I>How is it connected to your major (electrical engineering)?</i><br> | |||
Capacitors and electrical engineering inadvertently go hand-in-hand. Whether developing filters, storing data, or making these kinds of sensors, there is a wide array of applications. | |||
===Connection to Industry: Fuel Gauge Level Sensing=== | |||
<I>Is there an interesting industrial application?</i><br> | |||
The concept of capacitative fluid level sensing is the same for any fluid, and fuel is no outlier. In some aircraft, the fuel level is measured using this technique and relayed to the pilot in the cockpit. | |||
== See also == | == See also == | ||
*[[Capacitor]] for an overview of capacitors, | |||
*[[VPython]] to understand the computational model, | |||
*[[Dielectric]] to read about dielectrics | |||
===Further reading=== | ===Further reading=== | ||
*[http://hyperphysics.phy-astr.gsu.edu/hbase/electric/capcyl.html Hyperphysics.phy-astr.gsu.edu] for a description of cylindrical capacitors. | |||
===External links=== | ===External links=== | ||
[http://www. | *[http://www.sensorsmag.com/sensors/leak-level/a-dozen-ways-measure-fluid-level-and-how-they-work-1067 Sensor Online] for a list of fluid level measurement techniques | ||
==References== | ==References== | ||
#[http://auto.howstuffworks.com/fuel-gauge1.htm HowStuffWorks], measuring fuel in a car | |||
#[http://www.facstaff.bucknell.edu/mastascu/elessonshtml/LC/Capac1.htm Falstaff.bucknell.edu], a long overview of capacitors | |||
#[http://hyperphysics.phy-astr.gsu.edu/hbase/electric/capac.html Hyperphysics.phy-astr.gsu.edu], describing capacitance | |||
#[http://hyperphysics.phy-astr.gsu.edu/hbase/electric/pplate.html Hyperphysics.phy-astr.gsu.edu], capacitance of a parallel plate capacitor | |||
#[http://nvlpubs.nist.gov/nistpubs/jres/56/jresv56n1p1_A1b.pdf Nist.gov], an article describing the relationship of temperature to dielectric constant of water | |||
#[https://www.aea.net/AvionicsNews/ANArchives/FuelIndSystemsJan03.pdf AEA.net], describing fuel indication systems with capacitance | |||
[[Category:Real Life Applications of Electromagnetic Principles]] | |||
[[Category: | |||
Latest revision as of 21:54, 7 December 2015
Measuring the level of a fluid is useful for a variety of applications, and the technology for the techniques employed in the acquisition of this measurement has progressed far beyond the use of sight glasses and mechanical floats. In fact, a widely used method to measure the amount of fuel in a gas tank is with a device that floats on top of the fuel combined with a sensor, the fuel gauge sending unit, that translates the angle of the float to the amount of fluid in the tank. With this method, the gauge tends to change position with the angle of the car as well as the angle of the float relative to the fluid, so a lot of the time the gauge position can be misleading. A more modern technique of measuring fluid level involves capacitors, and this article will detail the concepts and mathematics behind the relationship with fluid height.
Structure of a Capacitor
For more details, see capacitor.
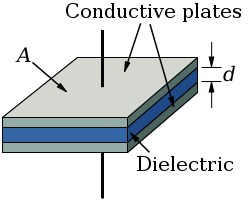
A capacitor consists of two conductors, e.g. conducting plates, separated by some kind of insulator. The insulator--a dielectric--within the gap between the two conductors can be air, plastic, glass, etc. Additionally, the conductors have to be connected to some sort of power supply in order to acquire a buildup of charge on the surface of the conductors.
The magnitude of the electric field within a capacitor is [math]\displaystyle{ \left| \vec{E}_{capacitor} \right| = \frac{Q/A}{\epsilon_{0}} }[/math], where the gap is only occupied by free space. [math]\displaystyle{ Q }[/math] is the charge on a plate and [math]\displaystyle{ A }[/math] is the area of a plate. Additionally, [math]\displaystyle{ \epsilon_{0} }[/math] is the permittivity of free space as detailed here.
Relating Capacitance to Fluid Level
With a dielectric involved, we apply the equation [math]\displaystyle{ \vec{E}_{dielectric} = \frac{\vec{E}_{applied}}{K} }[/math], where [math]\displaystyle{ K }[/math] is the dielectric constant of the material, and get [math]\displaystyle{ \left| \vec{E}_{dielectric} \right| = \frac{Q/A}{K\epsilon_{0}} }[/math]. The capacitance, [math]\displaystyle{ C=\frac{Q}{V} }[/math] (where [math]\displaystyle{ V }[/math] is the voltage) or [math]\displaystyle{ C=\frac{\epsilon_0 A K}{d} }[/math], therefore changes with a varying dielectric constant.
When multiple materials are between the gap, for instance water and air, the overall capacitance would be [math]\displaystyle{ C=\epsilon_0 A (d_{water}+d_{air})(\frac{K_{water}}{d_{water}}+\frac{K_{air}}{d_{air}}) }[/math], where [math]\displaystyle{ d=d_{water}+d_{air} }[/math] and [math]\displaystyle{ K_{air} \approx 1 }[/math]. Thus, correlating capacitance to known levels of water results in a calibration for a sensor using this technique, and the amount of water can be back calculated from the overall capacitance. With more than two dielectrics, the equation can be expanded to include these materials.
A Computational Model
For a simple simulation depicting how changing the amount of dielectric within the gap of a capacitor changes the corresponding electric field, please check out the VPython simulation. The charge on the capacitor as well as the dielectric constants for both dielectrics can be adjusted to visualize how the changes affect the electric field. Notice that the scale factor for the electric field is computed in such a way that the maximum length of the arrow is always the distance between the two plates, so adjusting constants proportionally may result in similar looking arrows (although the electric field will be different). Additionally, you can try changing the color on one of the dielectrics to better visualize the allocation of both within the gap of the capacitor.
A decrease in electric field yields an increase in capacitance, so we can imagine how these two are related. With water and air surrounded by plastic, determining the water level is as simple as measuring the capacitance and solving for the amount of water. In practical applications, these sensors would have to be calibrated and an additional temperature sensor would be needed, because the dielectric constant changes with temperature.
Examples
For an example, I will extract the scenario from a YouTube video here. We want to build a capacitor and measure the capacitance with varying dielectric content. Using simple materials like aluminum foil, some sort of insulating material (like "Press n Seal" plastic) to insulate the capacitor from the water, and a device capable of measuring capacitance, we can see that capacitance varies with water level and a correlation for a constant temperature can be developed.
Connectedness
Connection to Personal Interest: Water Level Sensing
How is this topic connected to something that you are interested in?
My father owns horses and in order to make sure they have water, he needed to walk far to check the troughs containing water. Instead, with assistance of videos part I and part II (although these sensors work off of resistance, the data transferring portion really helped), we were able to construct a capacitative water level sensor that transmitted the information to us in the house, without requiring long treks to monitor the water. Thus, the interest stemmed from a determination to do less work.
Connection to Major: Engineering Applications
How is it connected to your major (electrical engineering)?
Capacitors and electrical engineering inadvertently go hand-in-hand. Whether developing filters, storing data, or making these kinds of sensors, there is a wide array of applications.
Connection to Industry: Fuel Gauge Level Sensing
Is there an interesting industrial application?
The concept of capacitative fluid level sensing is the same for any fluid, and fuel is no outlier. In some aircraft, the fuel level is measured using this technique and relayed to the pilot in the cockpit.
See also
- Capacitor for an overview of capacitors,
- VPython to understand the computational model,
- Dielectric to read about dielectrics
Further reading
- Hyperphysics.phy-astr.gsu.edu for a description of cylindrical capacitors.
External links
- Sensor Online for a list of fluid level measurement techniques
References
- HowStuffWorks, measuring fuel in a car
- Falstaff.bucknell.edu, a long overview of capacitors
- Hyperphysics.phy-astr.gsu.edu, describing capacitance
- Hyperphysics.phy-astr.gsu.edu, capacitance of a parallel plate capacitor
- Nist.gov, an article describing the relationship of temperature to dielectric constant of water
- AEA.net, describing fuel indication systems with capacitance