Light Propagation Through a Medium: Difference between revisions
No edit summary |
No edit summary |
||
| (31 intermediate revisions by the same user not shown) | |||
| Line 6: | Line 6: | ||
===A Mathematical Model=== | ===A Mathematical Model=== | ||
The speed of light through a medium can be given by the formula n=(c/v), where n is the index of refraction, v is the velocity of light through the medium and c is the speed of light through a vacuum. | The speed of light through a medium can be given by the formula n=(c/v), where n is the index of refraction, v is the velocity of light through the medium and c is the speed of light through a vacuum. | ||
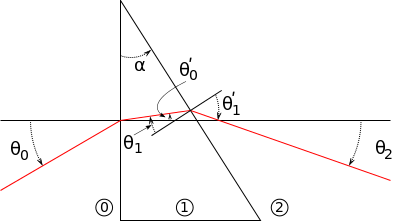
The relationship between the angle of incidence and angle of refraction when light passes through a medium is given by Snell's Law. | The relationship between the angle of incidence and angle of refraction when light passes through a medium is given by Snell's Law. :<math>n_1\sin\theta_1 = n_2\sin\theta_2\ </math> | ||
[[File:RefractionReflextion.svg]] | |||
===A Computational Model=== | ===A Computational Model=== | ||
[[File: | [[File:Snells_law_wavefronts.gif]] | ||
==Examples== | ==Examples== | ||
===Easy=== | ===Easy=== | ||
The speed of light is | The speed of light is found as 2.96E8 m/s, What is the index of refraction that relates to the material. | ||
====Solution==== | ====Solution==== | ||
The index of refraction is n=(c/v), n=(3.00E8)/(2.76E8) = 1. | The index of refraction is n=(c/v), n=(3.00E8)/(2.76E8) = 1.01. | ||
===Medium=== | ===Medium=== | ||
What is the index of refraction if the angle of incidence in air is 30 degrees and the angle of refraction is 15 degrees? | |||
====Solution==== | |||
solving for n2 in snells law gives (1*sin(30))/sin(15) = 1.93 | |||
===Difficult=== | ===Difficult=== | ||
Light passes from air into glass at an angle of 20 degrees with respect to the normal. What is the angle of refraction? | |||
====Solution==== | |||
Plugging into Snell's Law gives 1.00sin(20)=1.50sin(theta), solving for theta gives a value of 13.2 degrees. | |||
==Connectedness== | ==Connectedness== | ||
===Telecommunications=== | |||
One extremely important use of Snell's Law and light propagation through a medium is telecommunications. Fiber optics take advantage of Snell's Law to send large amounts of data. Since these fiber optics cables are not laid out in straight lines the light beams refract significantly and index of refraction are used to guide the light beam through the cable. | |||
[[File:Optical-fibre.svg]] | |||
===Human Body=== | |||
The human makes use of Snell's Law to give us the ability to see objects. This is because in the human eye there is a natural lens which refracts light onto the optic nerve and allows our brain to make sense of the light that is entering our eye. | |||
===Optics=== | |||
There are many facets of optics that take advantage of refraction and how light changes when it propagates through a medium. On such sub field of optics are lenses. Lenses make use of refraction of light to make many modern inventions possible like projectors, cameras, and telescopes. Also, any inventions that make use of prisms take advantage of the refraction of light. | |||
[[File:Prism ray trace.svg]] | |||
===My Interests/Major=== | |||
My major is Industrial Engineering and I am interested in the topic of optics, this study of how light propagates through a medium is the foundation of optics. This relates to my major because my major has a lot to do with manufacturing and many aspects of optics and refraction are used in manufacturing. | |||
==History== | ==History== | ||
Much of the history of Light Propagation through a medium has to do with research into refraction angles. Ptolemy was the first person to try to find a relationship between refraction angles. Alhazen was another researcher who published studies into optics around the year 1021. The next breakthrough in this field was done by a Dutch Astronomer named Willebrord Snellius, although the law that is named after him was actually discovered by a Persian scientist Ibn Sahl. Over the 1600s the field of optics which takes advantage of refraction made rapid strides. In 1678, Christian Huygens showed how Snell's Law related to the wave nature of light and developed the Huygens–Fresnel principle. Finally, in the 20th century Snell's Law was brought back to relevance by the discovery of modern optical and electromagnetic theories. | |||
==See Also== | ==See Also== | ||
*[[Refraction]] | |||
*[[Lenses]] | |||
==References== | |||
http://physicsabout.com/refraction-of-light/ | |||
https://eng.libretexts.org/Core/Materials_Science/Optical_Properties/Snell's_Law | |||
http://scienceworld.wolfram.com/physics/SnellsLaw.html | |||
https://byjus.com/physics/wp-content/uploads/2016/06/8-2.png | |||
==List of Refractive Indexes== | |||
Vacuum - 1, | |||
Air - 1.000293, | |||
Hydrogen - 1.000132, | |||
Helium - 1.000036, | |||
Water - 1.333, | |||
Olive Oil - 1.47, | |||
Ice - 1.31, | |||
Plexiglass - 1.49, | |||
Glass - 1.62, | |||
Sapphire - 1.77, | |||
Diamond - 2.42, | |||
Latest revision as of 12:07, 25 November 2017
This page is going to be about about Light Propagation. A work in progress . Edited by Roshan Konda Fall 2017
The Main Idea
When light travels through anything but a vacuum the speed of light travels at a speed different from c=3.00E8 m/s and the light particles scatter. The highest speed that light can travel though is the universal constant c. Light also refracts, or changes direction when it enters a new medium.
A Mathematical Model
The speed of light through a medium can be given by the formula n=(c/v), where n is the index of refraction, v is the velocity of light through the medium and c is the speed of light through a vacuum. The relationship between the angle of incidence and angle of refraction when light passes through a medium is given by Snell's Law. :[math]\displaystyle{ n_1\sin\theta_1 = n_2\sin\theta_2\ }[/math]
A Computational Model
Examples
Easy
The speed of light is found as 2.96E8 m/s, What is the index of refraction that relates to the material.
Solution
The index of refraction is n=(c/v), n=(3.00E8)/(2.76E8) = 1.01.
Medium
What is the index of refraction if the angle of incidence in air is 30 degrees and the angle of refraction is 15 degrees?
Solution
solving for n2 in snells law gives (1*sin(30))/sin(15) = 1.93
Difficult
Light passes from air into glass at an angle of 20 degrees with respect to the normal. What is the angle of refraction?
Solution
Plugging into Snell's Law gives 1.00sin(20)=1.50sin(theta), solving for theta gives a value of 13.2 degrees.
Connectedness
Telecommunications
One extremely important use of Snell's Law and light propagation through a medium is telecommunications. Fiber optics take advantage of Snell's Law to send large amounts of data. Since these fiber optics cables are not laid out in straight lines the light beams refract significantly and index of refraction are used to guide the light beam through the cable.

Human Body
The human makes use of Snell's Law to give us the ability to see objects. This is because in the human eye there is a natural lens which refracts light onto the optic nerve and allows our brain to make sense of the light that is entering our eye.
Optics
There are many facets of optics that take advantage of refraction and how light changes when it propagates through a medium. On such sub field of optics are lenses. Lenses make use of refraction of light to make many modern inventions possible like projectors, cameras, and telescopes. Also, any inventions that make use of prisms take advantage of the refraction of light.
My Interests/Major
My major is Industrial Engineering and I am interested in the topic of optics, this study of how light propagates through a medium is the foundation of optics. This relates to my major because my major has a lot to do with manufacturing and many aspects of optics and refraction are used in manufacturing.
History
Much of the history of Light Propagation through a medium has to do with research into refraction angles. Ptolemy was the first person to try to find a relationship between refraction angles. Alhazen was another researcher who published studies into optics around the year 1021. The next breakthrough in this field was done by a Dutch Astronomer named Willebrord Snellius, although the law that is named after him was actually discovered by a Persian scientist Ibn Sahl. Over the 1600s the field of optics which takes advantage of refraction made rapid strides. In 1678, Christian Huygens showed how Snell's Law related to the wave nature of light and developed the Huygens–Fresnel principle. Finally, in the 20th century Snell's Law was brought back to relevance by the discovery of modern optical and electromagnetic theories.
See Also
References
http://physicsabout.com/refraction-of-light/
https://eng.libretexts.org/Core/Materials_Science/Optical_Properties/Snell's_Law
http://scienceworld.wolfram.com/physics/SnellsLaw.html
https://byjus.com/physics/wp-content/uploads/2016/06/8-2.png
List of Refractive Indexes
Vacuum - 1, Air - 1.000293, Hydrogen - 1.000132, Helium - 1.000036, Water - 1.333, Olive Oil - 1.47, Ice - 1.31, Plexiglass - 1.49, Glass - 1.62, Sapphire - 1.77, Diamond - 2.42,

