Potential Difference in a non-Uniform Field: Difference between revisions
| (21 intermediate revisions by the same user not shown) | |||
| Line 26: | Line 26: | ||
==Examples== | ==Examples== | ||
===Simple Example=== | |||
[[File:NonUniEx1.png | center | 200px | Simple Example for non-Uniform Fields]] | |||
Is the total field above a non-Uniform Field or a Uniform Field? What about the first (-left-) section by itself? | |||
'''Answer:''' | |||
Total- Non-Uniform Field | |||
First Section- Uniform Field | |||
===Symbolic Example=== | |||
[[File:NonUniEx1.png | center | 300px | Calculating Potential Difference from A to B- in a non-Uniform Field]] | [[File:NonUniEx1.png | center | 300px | Calculating Potential Difference from A to B- in a non-Uniform Field]] | ||
| Line 31: | Line 45: | ||
Create a point in between the boundaries of the two Electric Fields, and use this point to calculate the individual potential differences. | Create a point in between the boundaries of the two Electric Fields, and use this point to calculate the individual potential differences. | ||
* Calculate from A to the center | * Calculate Potential Difference from A to the center | ||
* Calculate from the center to B | * Calculate Potential Difference from the center to B | ||
* Add the values above to get the Potential Difference from A to B | |||
:<math>\Delta V_1</math> = | :<math>\Delta V_1</math> = -(<math>E1_{x}</math>●<math>(Center_x - A_x)</math>) | ||
:<math>\Delta V_2</math> = -(<math>E1_{x}</math>●<math>(B_x - Center_x)</math>) | |||
:<math>\Delta V_{total}</math> = <math>\Delta V_1</math> + <math>\Delta V_2</math> | |||
''Since all y-values and z-values are zero, they are not considered in the equations above. If they were present (differences in y-values and z-values), then they would be calculated as usual.'' | |||
==Connectedness== | ==Connectedness== | ||
This is highly relevant to modern applications because in the real-world a majority of situations will deal with a combination of various Electric Fields or a source that varies. | |||
==History== | ==History== | ||
Volt (unit) - Sir Charles Bright and Latimer Clark decided to represent a unit of resistance as "Volt." This unit was named Volt because of Alessandro Volta, the person who developed the voltaic pile- producing a more or less reliable, steady electric current. | |||
Alessandro Volta - Italian physicist and chemist that led to the development of the study of electrochemistry through various experiments that debunked the myth that only living things created electricity. Due to his original experiments, Alessandro Volta pushed other scientists to make new developments about electricity and their application. | |||
==See also== | |||
''Potential Difference of a Point Charge in a Non-Uniform Field'' | |||
*http://www.physicsbook.gatech.edu/Potential_Difference_of_Point_Charge_in_a_Non-Uniform_Field | |||
''Potential Difference in a Uniform Field'' | |||
*http://www.physicsbook.gatech.edu/Potential_Difference_in_a_Uniform_Field | |||
https:// | ===External links=== | ||
====Further Reading==== | |||
''Applications of Non-Uniform Electric Fields'' | |||
*https://pubs.rsc.org/-/content/articlepdf/1966/tf/tf9666203484 | |||
https://www. | ''Use of Spatially Non-Uniform Electric Fields for | ||
Contact-Free Assembly of Three-Dimensional | |||
Structures from Colloidal Particles'' | |||
*https://www.mobt3ath.com/uplode/book/book-12811.pdf | |||
https://www.youtube.com/watch?v=vj2zLThvf-c | ====Videos==== | ||
''Video Lectures and Examples'' | |||
*https://www.youtube.com/watch?v=j2k6LDafXHI | |||
*https://www.youtube.com/watch?v=LG2t1_acgik | |||
*https://www.youtube.com/watch?v=qki3pTacXBE | |||
*https://www.youtube.com/watch?v=vj2zLThvf-c | |||
==References== | ==References== | ||
Latest revision as of 14:31, 25 November 2018
Dalton Lewis Fall 2018
Main Idea
Fields
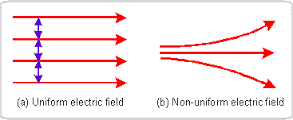
Uniform Field: If the magnitude and direction of an electric field at each and every point in a region is the same, the field in that region is uniform. More specifically, if the electric field vector doesn't vary with position. Non-Uniform Field: If the magnitude and direction of an electric field is different at some point in the region, the field in that region is considered non-uniform.
Electric Field Models: When looking at the graphs below, the Uniform Field has parallel and equal magnitude arrows throughout the region whereas the Non-Uniform Field will have points that go other directions at some point.
Potential Difference
Potential difference is the change in electric potential between a final and initial location. The work done on the charge during this movement will alter its potential energy and because of this change in potential energy, there is a difference in electric potential between these locations.
When considering Potential Difference calculated in non-Uniform Fields, the regions should be split into smaller sections of Uniform Fields. For example, the path from the initial location to the final location passes through two regions of uniform, but different fields. In this case, you would split this into two separate calculations for each region and then combine to determine the total potential difference
Mathematical Model
- [math]\displaystyle{ \Delta V }[/math] = [-([math]\displaystyle{ E1_{x} }[/math]●[math]\displaystyle{ \Delta x }[/math] + [math]\displaystyle{ E1_{y} }[/math]●[math]\displaystyle{ \Delta y }[/math] + [math]\displaystyle{ E1_{z} }[/math]●[math]\displaystyle{ \Delta z }[/math])] + [-([math]\displaystyle{ E2_{x} }[/math]●[math]\displaystyle{ \Delta x }[/math] + [math]\displaystyle{ E2_{y} }[/math]●[math]\displaystyle{ \Delta y }[/math] + [math]\displaystyle{ E2_{z} }[/math]●[math]\displaystyle{ \Delta z }[/math]] + ... = -[math]\displaystyle{ \Sigma \vec{E} }[/math]●[math]\displaystyle{ \Delta \vec{l} }[/math]
Computational Model
Examples
Simple Example
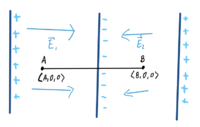
Is the total field above a non-Uniform Field or a Uniform Field? What about the first (-left-) section by itself?
Answer:
Total- Non-Uniform Field
First Section- Uniform Field
Symbolic Example
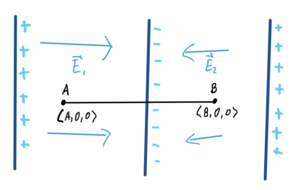
For this problem, you will need to split the path into two separate parts. In this case, the potential difference will be calculated from location A to B
Create a point in between the boundaries of the two Electric Fields, and use this point to calculate the individual potential differences.
- Calculate Potential Difference from A to the center
- Calculate Potential Difference from the center to B
- Add the values above to get the Potential Difference from A to B
- [math]\displaystyle{ \Delta V_1 }[/math] = -([math]\displaystyle{ E1_{x} }[/math]●[math]\displaystyle{ (Center_x - A_x) }[/math])
- [math]\displaystyle{ \Delta V_2 }[/math] = -([math]\displaystyle{ E1_{x} }[/math]●[math]\displaystyle{ (B_x - Center_x) }[/math])
- [math]\displaystyle{ \Delta V_{total} }[/math] = [math]\displaystyle{ \Delta V_1 }[/math] + [math]\displaystyle{ \Delta V_2 }[/math]
Since all y-values and z-values are zero, they are not considered in the equations above. If they were present (differences in y-values and z-values), then they would be calculated as usual.
Connectedness
This is highly relevant to modern applications because in the real-world a majority of situations will deal with a combination of various Electric Fields or a source that varies.
History
Volt (unit) - Sir Charles Bright and Latimer Clark decided to represent a unit of resistance as "Volt." This unit was named Volt because of Alessandro Volta, the person who developed the voltaic pile- producing a more or less reliable, steady electric current.
Alessandro Volta - Italian physicist and chemist that led to the development of the study of electrochemistry through various experiments that debunked the myth that only living things created electricity. Due to his original experiments, Alessandro Volta pushed other scientists to make new developments about electricity and their application.
See also
Potential Difference of a Point Charge in a Non-Uniform Field
Potential Difference in a Uniform Field
External links
Further Reading
Applications of Non-Uniform Electric Fields
Use of Spatially Non-Uniform Electric Fields for Contact-Free Assembly of Three-Dimensional Structures from Colloidal Particles
Videos
Video Lectures and Examples
- https://www.youtube.com/watch?v=j2k6LDafXHI
- https://www.youtube.com/watch?v=LG2t1_acgik
- https://www.youtube.com/watch?v=qki3pTacXBE
- https://www.youtube.com/watch?v=vj2zLThvf-c