First Law of Thermodynamics: Difference between revisions

From Physics Book
Jump to navigation Jump to search
 
(61 intermediate revisions by 2 users not shown)
Line 1: Line 1:
[[File:Thermo.jpg|300px|thumb|right]]Claimed by Mlee406 for fall 2016
==Main Idea==
The First Law of Thermodynamics is another way to state [[Conservation of Energy]] and [[The Energy Principle]]. Hence, if needed, review those topics before diving into The First Law of Thermodynamics. Heat, the transfer of thermal energy, and internal energy, the energy possessed by the constituents of the system, are forms of energy, just like [[Kinetic Energy]] and [[Potential Energy]]. We can now extend the scope of the Law of Conservation of Mechanical Energy from Work and external potential and kinetic energy to Heat and internal energy. The First Law of Thermodynamics states: although energy comes in various forms, the total quantity of energy stays the same, and the energy disappearing in one form must appear simultaneously in other forms.


The science of thermodynamics originated in the 19th century in order to explain the mechanism of steam engines. The term 'thermodynamics' means power developed from heat, and thermodynamics deals with the relationship between heat and other forms of energy. One can apply thermodynamics to a problem, beginning with identifying a body of matter called system. A system's thermodynamics state is defined by several macroscopic properties that depend on the fundamental dimensions such as time, temperature, mass, length, and etc.
[[File:Firstlaw.jpg|500px|center]]


==Background==
===Mathematical Model===
[[File:workheat.jpg|right]]
The First Law of Thermodynamics states:


===Joule's Experiment: Mechanical Equivalent of Heat===
:The change in internal energy of a system is equal to the heat added/taken away from the system plus the work done on the system/minus the work done by the system:
James P. Joule's experiments made major contributions to the formation of the modern concept of heat. Joule put certain amounts of mercury, water, and oil into an insulated container and mixed the liquid using a rotating stirrer. He carefully measured how much work was done by the stirrer to the liquid and the change in temperature that the liquid experienced. Joule discovered that for a particular fluid, a fixed amount of work is required per unit mass in order to raise its temperature by one degree. Joule established that heat is a form of energy and that there is a quantitative relationship between heat and work.


[[File:GW635H289.jpg]]
::<math>\Delta U_{system} = Q + W_{on system} \quad \Delta U_{system} = Q - W_{by system}</math>


===Internal Energy===
:<math>Q</math> and <math>W</math> are qualitatively energy in transit from the source to the receiver.
In Joule's experiment, work added to the liquid was transformed into heat. The energy in between the transition is contained in the liquid in a different form, called internal energy.
It is named 'internal' in order to distinguish it from kinetic and potential energy, which can be considered 'external', as they depend on the substance's position or motion. Internal energy cannot be measured directly and its absolute values are unknown. However, this is no problem as we are only concerned with changes in internal energy in thermodynamics.


==The Main Idea==
:The work done on a system is equal to the negative of the work done by the system:
It is crucial to recognize heat and internal energy as forms of energy through the previous section to understand the first law of thermodynamics.
We can now extend scope of the law of conservation of mechanical energy from work and external potential and kinetic energy to heat and internal energy.
First Law of Thermodynamics states, although energy comes in various forms, the total quantity of energy stays the same and the energy disappearing in one form must appear simultaneously in other forms.


===A Mathematical Model===
::<math>W_{on system} = -W_{by system}</math>


In the thermodynamics analysis, system is the region in which the process takes place in and the surroundings are everything that the system interacts with.  
[[File:Thermo1.gif|right|500px]]
First law is applied to the system and its surroundings,
<math>∆</math>(Energy of the system) + <math>∆</math>(Energy of surroundings) <math>= 0</math>


In a closed system, no streams enter nor leave the system and there is no transfer of matter across the boundary of system and its surroundings.
The First Law of Thermodynamics can also be stated in a more general fashion as:
All exchange in energy occur as heat and work and total energy change is the net energy transported as heat or work.


<math>∆U = Q+W</math> where <math>∆U</math> is change in the internal energy , <math>Q</math> is heat added to the system, and <math>W</math> is the work done by or done on the system. In other words, change in internal energy is equal to flow of heat into a system plus the work done by or on the system. 
:The change in total energy of the system is equal to the heat added/taken away from the system plus the work done on the system/minus the work done by the system:
<math>Q</math> and <math>W</math> are energy in transit; they are never stored nor contained in the body. Whereas,  potential, kinetic, and internal energy are stored with the matter. While both <math>Q</math> and <math>W</math> are path functions, <math>∆U</math> is a path-independent state function, which means that it only depends on the current state of the system.


First Law of Thermodynamics may also be written as:
::<math>\Delta E_{total} = \Delta PE + \Delta KE + \Delta U \quad \Delta E_{total} = Q + W</math>, where


<math>E^t</math> = Total Energy, <math>KE</math> = Kinetic Energy, <math>PE</math>=Potential Energy
:::<math>\Delta PE =</math> change in potential energy of the system


<math>∆E^t = ∆KE + ∆PE + ∆U</math>
:::<math>\Delta KE =</math> change in kinetic energy of the system


<math>∆E^t = Q + W</math>
:::<math>\Delta U =</math> change in internal energy of the system


<math>∆KE + ∆PE + ∆U = Q + W</math>
:Therefore:


===A Computational Model===
::<math>\Delta PE + \Delta KE + \Delta U = Q + W</math>
 
:The quantity <math>\Delta PE + \Delta KE</math> is usually considered <math>0</math> by [[The Energy Principle]], leading to the previous equation of The First Law of Thermodynamics..
 
===Computational Model===
:'''Insert Computational Model here'''


http://jersey.uoregon.edu/vlab/Thermodynamics/
http://jersey.uoregon.edu/vlab/Thermodynamics/
Line 50: Line 48:


===Simple===
===Simple===
Heat of 5000J is added to a closed system and the internal energy is decreased by 11000J. How much energy is transferred as work?  
<math>5,000 \ J</math> of Heat is added to a closed system. Also, the internal energy of the system decreases by <math>11,000 \ J</math>.
 
:'''a) How much Work must the system have done?'''


Solution:
::Referring to our [[First Law of Thermodynamics#Mathematical Model| Mathematical Model]], we know for a closed system, the change in internal energy of a the system is equal to the Heat applied to the system/lost by the system plus the Work done on the system:


<math>∆U = Q + W</math>, <math>Q= 5000J</math>, <math>∆U=-11000 J</math>
:::<math>\Delta U_{system} = Q + W_{on system}</math>


<math>-11000J = 5000J + W</math>
::We know the Heat added and the change in internal energy of the system. Therefore, we can find the Work done by the system by noting the Work on the system is equal to the negative of the Work done by the system:


<math>W = -11000J-5000J</math>
:::<math>W_{on system} = -W_{bysystem}</math>


<math>W = -16000J</math>
:::<math>W_{on system} = \Delta U_{system} - Q</math>
 
:::<math>W_{bysystem} = -( \Delta U_{system} - Q)</math>
 
:::<math>W_{bysystem} = -(-11,000 - 5,000) = 16,000 \ J</math>
 
:The system must have done <math>16,000 \ J</math> of Work to explain the loss in internal energy but addition of Heat.


===Middling===
===Middling===
An egg, initially at rest, is dropped onto a concrete surface and breaks. Treat the egg as the system.
An egg, initially at rest, is dropped onto a concrete surface and breaks. Treat the egg as the system.


a) What is the sign of <math>W</math>?
:'''a) What is the sign of <math>W</math>?'''
 
::Since the egg is speeding up as it falls, Work must be being done on the egg. Thus, <math>W_{onegg}</math> is positive, and <math>W_{byegg}</math> is negative, since:
 
:::<math>W_{onegg} = -W_{by egg}</math>
 
:'''b) What is the sign of <math>\Delta PE</math>?'''
 
::The change in potential energy of the egg will be negative, since it is falling towards the Earth. Let <math>h_0</math> and <math>h_f</math> be the initial and final height of the egg, respectively with <math>h_f << h_0</math>, then we have:


b) What is the sign of <math>∆PE</math>?
:::<math>\Delta PE = mgh_f - mgh_0 = mg(h_f - h_0) < 0</math>, since <math>h_f << h_0</math>


c) What is <math>∆KE</math>?
:'''c) What is <math>\Delta KE</math>?'''


d) What is <math>∆U</math>?
::The change in kinetic energy of the egg is <math>0</math>, due to the fact that its initial and final velocity are both <math>0</math>:


e) What is the sign of <math>Q</math>?
:::<math>\Delta KE = \frac{1}{2}m{v_f}^2 - \frac{1}{2}m{v_0}^2 = \frac{1}{2}m({v_f}^2 - {v_0}^2) \quad \And \quad v_f = v_0 = 0 \quad \therefore \quad \Delta K = 0</math>


Solution:
:'''d) What is <math>\Delta U</math>?'''


Utilizing <math>∆KE+∆PE+∆U=Q+W</math>
::No Heat is added to the system, and no chemical processes are in motion with the egg. Therefore, we can assume the internal energy of the egg is constant:


a) No work is done on the system + no work is done by the system to the surroundings, thus <math>W</math> = 0.
:::<math>\Delta U = 0</math>


b) Egg is falling from a higher surface, which means the elevation is decreased and the sign of <math>∆PE</math> is negative (-).
:'''e) What is the sign of <math>Q</math>?'''


c) Because the egg is at rest for both the initial and final state, <math>∆KE</math> = 0.
::From our [[First Law of Thermodynamics#Mathematicla Model| Mathematical Model]], we see:


d) The chemical state of egg does not change (it does not get scrambled), thus <math>∆U</math> = 0.
:::<math>\Delta PE + \Delta KE + \Delta U = Q + W_{onegg}</math>


e) From the above equation, the values with zero (<math>W</math>, <math>∆PE</math>, and <math>∆KE</math>) can all be cancelled and <math>∆PE</math> would equal <math>Q</math>.
::We also know:


<math>∆PE = Q </math>
:::<math>\Delta PE < 0</math>


Because the <math>∆PE</math> is negative(-), <math>Q</math> is also negative.
:::<math>\Delta KE = 0</math>
 
:::<math>\Delta U = 0</math>
 
:::<math>W_{onegg} > 0</math>
 
::So:
 
:::<math>Q = \Delta PE - W_{onegg}</math>
 
::We have <math>Q</math> set equal to a negative quantity minus a positive quantity. Therefore, <math>Q</math> must be a negative quantity its self:
 
:::<math>Q < 0</math>


===Difficult===
===Difficult===
One mole of gas in a closed system undergoes a four-step thermodynamic cycle. Using the below data, determine numerical values for the missing quantities.
One mole of gas in a closed system undergoes a four-step Thermodynamic cycle. Using the data below, determine the numerical values for the missing quantities.
 
{| class="wikitable" style="text-align:center; width:250px; height:250px; font-size:14pt;  border:10; frame:border; rules:all; margin-left:auto; margin-right:auto"
|+ Four Step Thermodynamic Cycle
|-
! style="border-width:3px; border-color:black; background: white" | Step
! style="border-width:3px; border-color:black; background: white" | <math>\Delta U \ (J)</math>
! style="border-width:3px; border-color:black; background: white" | <math>Q \ (J)</math>
! style="border-width:3px; border-color:black; background: white" | <math>W_{by gas} \ (J)</math>
|-
| style="background: white; border-width:3px; border-color:black" | <math>1 \rightarrow 2</math>
| <math>-200</math>
| style="background: yellow" | '''?'''
| <math>-6,000</math>
|-
| style="background: white; border-width:3px; border-color:black" | <math>2 \rightarrow 3</math>
| style="background: yellow" | '''?'''
| <math>-3,800</math>
| style="background: yellow" | '''?'''
|-
| style="background: white; border-width:3px; border-color:black" | <math>3 \rightarrow 4</math>
| style="background: yellow" | '''?'''
| <math>-800</math>
| <math>300</math>
|-
| style="background: white; border-width:3px; border-color:black" | <math>4 \rightarrow 1</math>
| <math>4,700</math>
| style="background: yellow" | '''?'''
| style="background: yellow" | '''?'''
|-
| style="background: white; border-width:3px; border-color:black" | <math>1 \rightarrow2 \rightarrow 3 \rightarrow 4 \rightarrow 1</math>
| style="background: yellow" | '''?'''
| style="background: yellow" | '''?'''
| <math>-1,400</math>
|}
 
The equation we will use for this example is:
 
:<math>\Delta U = Q + W_{ongas}</math>
 
:''First Analysis'':
 
::'''Step''' <math>[1 \rightarrow 2]</math>:
 
:::In-between steps 1 and 2, we can see from the table that the internal energy of the gas decreases by 200 Joules, and the gas does 6,000 Joules of Work on the surroundings. Thus, we can solve for the heat added/lost:
 
::::<math>Q(12) = \Delta U(12) - W_{on gas}(12) = \Delta U(12) + W_{bygas}(12) = -200 -  6,000 = -6,200 \ J</math>
 
::'''Step''' <math>[2 \rightarrow 3]</math>:
 
::In-between steps 2 and 3, we can see from the table that the heat lost by the gas is 3,800 Joules. This is not enough information to solve for anything, so we'll move onto the next step.
 
::'''Step''' <math>[3 \rightarrow 4]</math>:
 
:::In-between steps 3 and 4, we can see from the table that the heat lost by the system is 800 Joules, and the Work done by the gas is 300 Joules. Thus, we can solve for the change in internal energy:
 
::::<math>\Delta U(34) = Q(34) + W_{ongas}(34) = Q(34) - W_{bygas}(34)</math>
 
::::<math>\Delta U = -800 - 300 = -1,100 \ J</math>
 
::'''Step''' <math>[4 \rightarrow 1]</math>:
 
:::In-between steps 4 and 1, we see that the internal energy of the gas increases by 4,700 Joules. This is not enough information to solve for the components, so we'll move onto the next step.
 
::'''Step''' <math>[1 \rightarrow 2 \rightarrow 3 \rightarrow 4 \rightarrow 1]</math>:
 
:::This step signifies the whole cycle. In a cycle of a closed system, energy will be conserved, a fact we have been utilizing. This also means the change in internal energy will be a 0 Joules once we have completed the cycle. We can use this information:
 
::::<math>\Delta U(12341) = Q(12341) + W_{ongas}(12341) = Q(12341) - W_{bygas}(12341) = 0</math>
 
::::<math>Q(12341) = W_{bygas}(12341) = -1,400 \ J</math>
 
:::The change in internal energy is also equal to the sum of the changes of internal energy in each step. We can use this to solve for the change in internal between steps 2 and 3:
 
::::<math>\Delta U_{total} =  \Delta U_{12} + \Delta U_{23} + \Delta U_{34} + \Delta U_{41} = 0</math>


[[File:Thermo3.png]]
::::<math>\Delta U_{23} = - \Delta U_{12} - \Delta U_{34} - \Delta U_{41} = -(-200) - (-1,100) - (4,700) = 200 + 1,100 - 4,700 = - 3,400 \ J</math>
 
:''Second Analysis'':
 
{| class="wikitable" style="text-align:center; width:250px; height:250px; font-size:14pt;  border:10; frame:border; rules:all; margin-left:auto; margin-right:auto"
|+ Four Step Thermodynamic Cycle
|-
! style="border-width:3px; border-color:black; background: white" | Step
! style="border-width:3px; border-color:black; background: white" | <math>\Delta U \ (J)</math>
! style="border-width:3px; border-color:black; background: white" | <math>Q \ (J)</math>
! style="border-width:3px; border-color:black; background: white" | <math>W_{by gas} \ (J)</math>
|-
| style="background: white; border-width:3px; border-color:black" | <math>1 \rightarrow 2</math>
| <math>-200</math>
| <math>-6,200</math>
| <math>-6,000</math>
|-
| style="background: white; border-width:3px; border-color:black" | <math>2 \rightarrow 3</math>
| <math>-3,400</math>
| <math>-3,800</math>
| style="background: yellow" | '''?'''
|-
| style="background: white; border-width:3px; border-color:black" | <math>3 \rightarrow 4</math>
| <math>-1,100</math>
| <math>-800</math>
| <math>300</math>
|-
| style="background: white; border-width:3px; border-color:black" | <math>4 \rightarrow 1</math>
| <math>4,700</math>
| style="background: yellow" | '''?'''
| style="background: yellow" | '''?'''
|-
| style="background: white; border-width:3px; border-color:black" | <math>1 \rightarrow2 \rightarrow 3 \rightarrow 4 \rightarrow 1</math>
| <math>0</math>
| <math>-1,400</math>
| <math>-1,400</math>
|}
 
::Step [<math>2 \rightarrow 3</math>]:
 
:::We now have enough information to solve for the Work done by the gas in the step in-between 2 and 3:
 
::::<math>\Delta U(23) = Q(23) + W_{on gas}(23) = Q(23) - W_{by gas}(23)</math>
 
::::<math>W_{by gas}(23) = Q(23) - \Delta U(23) = -3,800 + 3,400 = -400 \ J</math>
 
::Step [<math>4 \rightarrow 1</math>]:
 
:::For the table to be self-consistent, the total in each column (bottom row) must equal the sum of the the other rows within that column. Thus:
 
::::<math>Q_{12341} = Q_{12} + Q_{23} + Q_{34} + Q_{41} \quad \And \quad W_{12341} = W_{12} + W_{23} + W_{34} + W_{41}</math>
 
::::<math>Q_{41} = Q_{12341} - (Q_{12} + Q_{23} + Q_{34}) \quad \And \quad W_{41} = W_{12341} - (W_{12} + W_{23} + W_{34})</math>
 
::::<math>Q_{41} = -1,400 - (-6,200 - 3,800 - 800) = -1,400 + 10,800 = 9,400 \ J</math>
 
::::<math>W_{41} = -1,400 - (-6,000 - 400 + 300) = -1,400 + 6,100 = 4,700 \ J</math>
 
We have filled in the table:
 
{| class="wikitable" style="text-align:center; width:250px; height:250px; font-size:14pt;  border:10; frame:border; rules:all; margin-left:auto; margin-right:auto"
|+ Four Step Thermodynamic Cycle
|-
! style="border-width:3px; border-color:black; background: white" | Step
! style="border-width:3px; border-color:black; background: white" | <math>\Delta U \ (J)</math>
! style="border-width:3px; border-color:black; background: white" | <math>Q \ (J)</math>
! style="border-width:3px; border-color:black; background: white" | <math>W_{by gas} \ (J)</math>
|-
| style="background: white; border-width:3px; border-color:black" | <math>1 \rightarrow 2</math>
| <math>-200</math>
| <math>-6,200</math>
| <math>-6,000</math>
|-
| style="background: white; border-width:3px; border-color:black" | <math>2 \rightarrow 3</math>
| <math>-3,400</math>
| <math>-3,800</math>
| <math>-400</math>
|-
| style="background: white; border-width:3px; border-color:black" | <math>3 \rightarrow 4</math>
| <math>-1,100</math>
| <math>-800</math>
| <math>300</math>
|-
| style="background: white; border-width:3px; border-color:black" | <math>4 \rightarrow 1</math>
| <math>4,700</math>
| <math>9,400</math>
| <math>4,700</math>
|-
| style="background: white; border-width:3px; border-color:black" | <math>1 \rightarrow2 \rightarrow 3 \rightarrow 4 \rightarrow 1</math>
| <math>0</math>
| <math>-1,400</math>
| <math>-1,400</math>
|}


==Connectedness==
==Connectedness==
1. How is this topic connected to something that you are interested in?
1. How is this topic connected to something that you are interested in?
* Thermodynamics is seen in all aspects of life, in everything from melting ice cubes to flipping switches to cooking.
*In physics, I've always encountered the subject of "Thermodynamics" with excitement. I always loved to deal with Temperatures and <math>mC \Delta T</math> is the equation that I enjoy utilizing the most. Being able to explain the mechanism of our fingers instantly turning cold as they touch the ice or in reverse, our hands warming up by simply holding a cup of hot cocoa as the flow of heat from a hotter object to colder object is inspring. Plus, there are even specific quantitative relationships that exist between the Heat, Work, and internal energy, and we are able to apply them exactly into our daily lives, thus the science of "Thermodynamics" is indeed extremely empowering!
2. How is it connected to your major?
2. How is it connected to your major?
* Thermodynamics is useful to know, and is covered in the Fundamentals of Engineering exam. Engineers interested in passing the FE and other similar tests should have a strong foundation in thermodynamics.
* I major in Chemical Engineering. There are two-semesters worth of curriculum dedicated solely to "Thermodynamics" in Chemical Engineering. The fundamental laws of Thermodynamics embody mathematical deduction to a network of equations which can be applied in all branches of science and engineering. Chemical Engineers provide solutions to a wide range of problems and, many of them have to do with calculating the Heat and Work for various physical and chemical processes. Thus, "Thermodynamics" is one of the skeletal parts of Chemical Engineering.


3. Is there an interesting industrial application?
3. Is there an interesting industrial application?
* Thermodynamics is relevant in the energy,transportation, and HVAC industries.
* Thermodynamics is relevant in the energy, transportation, petrochemical, and HVAC industries.
 
==History==
[[File:GW635H289.jpg|right]]
James P. Joule's experiments with Heat and Work made major contributions to the formation of the modern concept of Heat. Joule put certain amounts of mercury, water, and oil into an insulated container and mixed the liquid using a rotating stirrer. He carefully measured how much work was done by the stirrer to the liquid and the change in temperature that the liquid experienced. Joule discovered that for a particular fluid, a fixed amount of Work is required per unit mass in order to raise its Temperature by one degree. Joule established that Heat is a form of energy and that there is a quantitative relationship between Heat and Work.


== See also ==
[[File:Thermo.jpg|150px|right]]
[[File:Steam.jpeg|left|250px]]


[http://www.physicsbook.gatech.edu/Thermodynamics Thermodynamics]
The science of Thermodynamics originated in the 19th century in order to explain the mechanism of steam engines. The term 'Thermodynamics' means power developed from Heat, and Thermodynamics deals with the relationship between Heat and other forms of energy. One can apply Thermodynamics to a problem, beginning with identifying a body of matter called the system. A system's Thermodynamic state is defined by several macroscopic properties that depend on the fundamental dimensions such as time, temperature, mass, length, etc.


==See also==
===Further reading===
===Further reading===
* Thermodynamics (Dover Book on Physics) by Enrico Fermi
* Thermodynamics (Dover Book on Physics) by Enrico Fermi
Line 117: Line 314:
* M. J. Moran and H. N. Shapiro, ‘Fundamentals of Engineering Thermodynamics’,  Fourth Edition, Wiley, New York, 2000
* M. J. Moran and H. N. Shapiro, ‘Fundamentals of Engineering Thermodynamics’,  Fourth Edition, Wiley, New York, 2000
* Thermodynamics: An Engineering Approach by Cengel, Ya  and Boles, M.A.
* Thermodynamics: An Engineering Approach by Cengel, Ya  and Boles, M.A.
* Introduction to Chemical Engineering Thermodynamics, Seventh Edition, by J.M. Smith, H.C. Van Ness, M.M. Abbott


===External links===
===External links===
Line 124: Line 322:
* http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/firlaw.html
* http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/firlaw.html
* [http://www.wiley.com/college/moran/CL_0471465704_S/thermonet/docs/user/index.html ThermoNet]
* [http://www.wiley.com/college/moran/CL_0471465704_S/thermonet/docs/user/index.html ThermoNet]
*[https://www.khanacademy.org/science/physics/thermodynamics/laws-of-thermodynamics/v/first-law-of-thermodynamics-internal-energy Khan Academy: First Law of Thermodynamics]
* [https://www.khanacademy.org/science/physics/thermodynamics/laws-of-thermodynamics/v/first-law-of-thermodynamics-internal-energy Khan Academy: First Law of Thermodynamics]
* http://www.ncert.nic.in/html/learning_basket/energy10class/joule's%20experiment.htm
* http://demonstrations.wolfram.com/JoulesExperiment/
* https://www.wolframscience.com/reference/notes/1019b
* http://www.livescience.com/50776-thermodynamics.html
* [https://www.youtube.com/watch?v=5yOhSIAIPRE Mechanical Equivalent of Heat]
* https://en.wikipedia.org/wiki/First_law_of_thermodynamics
* https://courses.lumenlearning.com/introchem/chapter/the-three-laws-of-thermodynamics/
* https://www.khanacademy.org/science/physics/thermodynamics/laws-of-thermodynamics/a/what-is-the-first-law-of-thermodynamics
* http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/firlaw.html
* https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules_(Physical_and_Theoretical_Chemistry)/Thermodynamics/The_Four_Laws_of_Thermodynamics/First_Law_of_Thermodynamics


==References==
==References==
* Callen, Herbert B. (1985). Thermodynamics and an Introduction to Thermostatistics. Wiley. p. 5,37.
* Callen, Herbert B. (1985). Thermodynamics and an Introduction to Thermostatistics. Wiley. p. 5,37.
* http://fineartamerica.com/featured/1-thermodynamics-conceptual-artwork-richard-bizley.html
* http://fineartamerica.com/featured/1-thermodynamics-conceptual-artwork-richard-bizley.html
* http://www.humanthermodynamics.com/Clausius.html
* http://www.humanthermodynamics.com/Clausius.html
* http://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/node15.html
* http://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/node15.html
[[Category:Which Category did you place this in?]]
* http://www.juliantrubin.com/bigten/mechanical_equivalent_of_heat.html
* https://www.grc.nasa.gov/www/k-12/airplane/thermo1.html
* https://www2.estrellamountain.edu/faculty/farabee/biobk/BioBookEner1.html
* http://www2.phy.ilstu.edu/~hmb/phy325/TPCh.7.1(09).pdf
* http://www.shashaiseminar.com/notes/a-level/zimsec/physics/heat-2/
* https://www.asee.org/public/conferences/8/papers/4611/download

Latest revision as of 09:42, 4 August 2019

Main Idea

The First Law of Thermodynamics is another way to state Conservation of Energy and The Energy Principle. Hence, if needed, review those topics before diving into The First Law of Thermodynamics. Heat, the transfer of thermal energy, and internal energy, the energy possessed by the constituents of the system, are forms of energy, just like Kinetic Energy and Potential Energy. We can now extend the scope of the Law of Conservation of Mechanical Energy from Work and external potential and kinetic energy to Heat and internal energy. The First Law of Thermodynamics states: although energy comes in various forms, the total quantity of energy stays the same, and the energy disappearing in one form must appear simultaneously in other forms.

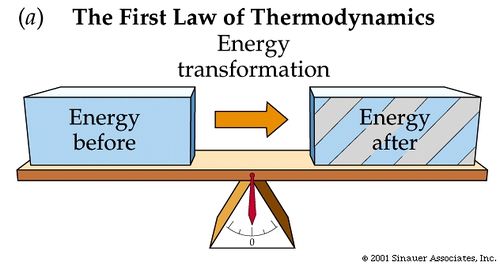
Mathematical Model

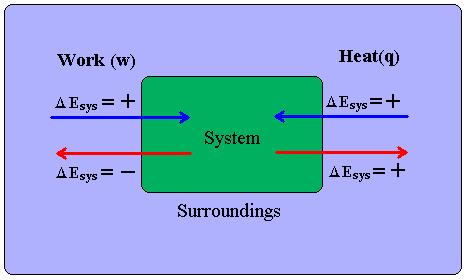
The First Law of Thermodynamics states:

The change in internal energy of a system is equal to the heat added/taken away from the system plus the work done on the system/minus the work done by the system:
[math]\displaystyle{ \Delta U_{system} = Q + W_{on system} \quad \Delta U_{system} = Q - W_{by system} }[/math]
[math]\displaystyle{ Q }[/math] and [math]\displaystyle{ W }[/math] are qualitatively energy in transit from the source to the receiver.
The work done on a system is equal to the negative of the work done by the system:
[math]\displaystyle{ W_{on system} = -W_{by system} }[/math]

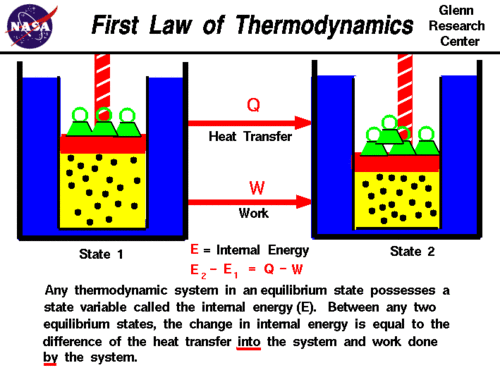
The First Law of Thermodynamics can also be stated in a more general fashion as:

The change in total energy of the system is equal to the heat added/taken away from the system plus the work done on the system/minus the work done by the system:
[math]\displaystyle{ \Delta E_{total} = \Delta PE + \Delta KE + \Delta U \quad \Delta E_{total} = Q + W }[/math], where
[math]\displaystyle{ \Delta PE = }[/math] change in potential energy of the system
[math]\displaystyle{ \Delta KE = }[/math] change in kinetic energy of the system
[math]\displaystyle{ \Delta U = }[/math] change in internal energy of the system
Therefore:
[math]\displaystyle{ \Delta PE + \Delta KE + \Delta U = Q + W }[/math]
The quantity [math]\displaystyle{ \Delta PE + \Delta KE }[/math] is usually considered [math]\displaystyle{ 0 }[/math] by The Energy Principle, leading to the previous equation of The First Law of Thermodynamics..

Computational Model

Insert Computational Model here

http://jersey.uoregon.edu/vlab/Thermodynamics/

This virtual experiment gives you visual representation of thermal equilibrium and how it is reached when beginning with different initial conditions.

Examples

Simple

[math]\displaystyle{ 5,000 \ J }[/math] of Heat is added to a closed system. Also, the internal energy of the system decreases by [math]\displaystyle{ 11,000 \ J }[/math].

a) How much Work must the system have done?
Referring to our Mathematical Model, we know for a closed system, the change in internal energy of a the system is equal to the Heat applied to the system/lost by the system plus the Work done on the system:
[math]\displaystyle{ \Delta U_{system} = Q + W_{on system} }[/math]
We know the Heat added and the change in internal energy of the system. Therefore, we can find the Work done by the system by noting the Work on the system is equal to the negative of the Work done by the system:
[math]\displaystyle{ W_{on system} = -W_{bysystem} }[/math]
[math]\displaystyle{ W_{on system} = \Delta U_{system} - Q }[/math]
[math]\displaystyle{ W_{bysystem} = -( \Delta U_{system} - Q) }[/math]
[math]\displaystyle{ W_{bysystem} = -(-11,000 - 5,000) = 16,000 \ J }[/math]
The system must have done [math]\displaystyle{ 16,000 \ J }[/math] of Work to explain the loss in internal energy but addition of Heat.

Middling

An egg, initially at rest, is dropped onto a concrete surface and breaks. Treat the egg as the system.

a) What is the sign of [math]\displaystyle{ W }[/math]?
Since the egg is speeding up as it falls, Work must be being done on the egg. Thus, [math]\displaystyle{ W_{onegg} }[/math] is positive, and [math]\displaystyle{ W_{byegg} }[/math] is negative, since:
[math]\displaystyle{ W_{onegg} = -W_{by egg} }[/math]
b) What is the sign of [math]\displaystyle{ \Delta PE }[/math]?
The change in potential energy of the egg will be negative, since it is falling towards the Earth. Let [math]\displaystyle{ h_0 }[/math] and [math]\displaystyle{ h_f }[/math] be the initial and final height of the egg, respectively with [math]\displaystyle{ h_f \lt \lt h_0 }[/math], then we have:
[math]\displaystyle{ \Delta PE = mgh_f - mgh_0 = mg(h_f - h_0) \lt 0 }[/math], since [math]\displaystyle{ h_f \lt \lt h_0 }[/math]
c) What is [math]\displaystyle{ \Delta KE }[/math]?
The change in kinetic energy of the egg is [math]\displaystyle{ 0 }[/math], due to the fact that its initial and final velocity are both [math]\displaystyle{ 0 }[/math]:
[math]\displaystyle{ \Delta KE = \frac{1}{2}m{v_f}^2 - \frac{1}{2}m{v_0}^2 = \frac{1}{2}m({v_f}^2 - {v_0}^2) \quad \And \quad v_f = v_0 = 0 \quad \therefore \quad \Delta K = 0 }[/math]
d) What is [math]\displaystyle{ \Delta U }[/math]?
No Heat is added to the system, and no chemical processes are in motion with the egg. Therefore, we can assume the internal energy of the egg is constant:
[math]\displaystyle{ \Delta U = 0 }[/math]
e) What is the sign of [math]\displaystyle{ Q }[/math]?
From our Mathematical Model, we see:
[math]\displaystyle{ \Delta PE + \Delta KE + \Delta U = Q + W_{onegg} }[/math]
We also know:
[math]\displaystyle{ \Delta PE \lt 0 }[/math]
[math]\displaystyle{ \Delta KE = 0 }[/math]
[math]\displaystyle{ \Delta U = 0 }[/math]
[math]\displaystyle{ W_{onegg} \gt 0 }[/math]
So:
[math]\displaystyle{ Q = \Delta PE - W_{onegg} }[/math]
We have [math]\displaystyle{ Q }[/math] set equal to a negative quantity minus a positive quantity. Therefore, [math]\displaystyle{ Q }[/math] must be a negative quantity its self:
[math]\displaystyle{ Q \lt 0 }[/math]

Difficult

One mole of gas in a closed system undergoes a four-step Thermodynamic cycle. Using the data below, determine the numerical values for the missing quantities.

Four Step Thermodynamic Cycle
Step [math]\displaystyle{ \Delta U \ (J) }[/math] [math]\displaystyle{ Q \ (J) }[/math] [math]\displaystyle{ W_{by gas} \ (J) }[/math]
[math]\displaystyle{ 1 \rightarrow 2 }[/math] [math]\displaystyle{ -200 }[/math] ? [math]\displaystyle{ -6,000 }[/math]
[math]\displaystyle{ 2 \rightarrow 3 }[/math] ? [math]\displaystyle{ -3,800 }[/math] ?
[math]\displaystyle{ 3 \rightarrow 4 }[/math] ? [math]\displaystyle{ -800 }[/math] [math]\displaystyle{ 300 }[/math]
[math]\displaystyle{ 4 \rightarrow 1 }[/math] [math]\displaystyle{ 4,700 }[/math] ? ?
[math]\displaystyle{ 1 \rightarrow2 \rightarrow 3 \rightarrow 4 \rightarrow 1 }[/math] ? ? [math]\displaystyle{ -1,400 }[/math]

The equation we will use for this example is:

[math]\displaystyle{ \Delta U = Q + W_{ongas} }[/math]
First Analysis:
Step [math]\displaystyle{ [1 \rightarrow 2] }[/math]:
In-between steps 1 and 2, we can see from the table that the internal energy of the gas decreases by 200 Joules, and the gas does 6,000 Joules of Work on the surroundings. Thus, we can solve for the heat added/lost:
[math]\displaystyle{ Q(12) = \Delta U(12) - W_{on gas}(12) = \Delta U(12) + W_{bygas}(12) = -200 - 6,000 = -6,200 \ J }[/math]
Step [math]\displaystyle{ [2 \rightarrow 3] }[/math]:
In-between steps 2 and 3, we can see from the table that the heat lost by the gas is 3,800 Joules. This is not enough information to solve for anything, so we'll move onto the next step.
Step [math]\displaystyle{ [3 \rightarrow 4] }[/math]:
In-between steps 3 and 4, we can see from the table that the heat lost by the system is 800 Joules, and the Work done by the gas is 300 Joules. Thus, we can solve for the change in internal energy:
[math]\displaystyle{ \Delta U(34) = Q(34) + W_{ongas}(34) = Q(34) - W_{bygas}(34) }[/math]
[math]\displaystyle{ \Delta U = -800 - 300 = -1,100 \ J }[/math]
Step [math]\displaystyle{ [4 \rightarrow 1] }[/math]:
In-between steps 4 and 1, we see that the internal energy of the gas increases by 4,700 Joules. This is not enough information to solve for the components, so we'll move onto the next step.
Step [math]\displaystyle{ [1 \rightarrow 2 \rightarrow 3 \rightarrow 4 \rightarrow 1] }[/math]:
This step signifies the whole cycle. In a cycle of a closed system, energy will be conserved, a fact we have been utilizing. This also means the change in internal energy will be a 0 Joules once we have completed the cycle. We can use this information:
[math]\displaystyle{ \Delta U(12341) = Q(12341) + W_{ongas}(12341) = Q(12341) - W_{bygas}(12341) = 0 }[/math]
[math]\displaystyle{ Q(12341) = W_{bygas}(12341) = -1,400 \ J }[/math]
The change in internal energy is also equal to the sum of the changes of internal energy in each step. We can use this to solve for the change in internal between steps 2 and 3:
[math]\displaystyle{ \Delta U_{total} = \Delta U_{12} + \Delta U_{23} + \Delta U_{34} + \Delta U_{41} = 0 }[/math]
[math]\displaystyle{ \Delta U_{23} = - \Delta U_{12} - \Delta U_{34} - \Delta U_{41} = -(-200) - (-1,100) - (4,700) = 200 + 1,100 - 4,700 = - 3,400 \ J }[/math]
Second Analysis:
Four Step Thermodynamic Cycle
Step [math]\displaystyle{ \Delta U \ (J) }[/math] [math]\displaystyle{ Q \ (J) }[/math] [math]\displaystyle{ W_{by gas} \ (J) }[/math]
[math]\displaystyle{ 1 \rightarrow 2 }[/math] [math]\displaystyle{ -200 }[/math] [math]\displaystyle{ -6,200 }[/math] [math]\displaystyle{ -6,000 }[/math]
[math]\displaystyle{ 2 \rightarrow 3 }[/math] [math]\displaystyle{ -3,400 }[/math] [math]\displaystyle{ -3,800 }[/math] ?
[math]\displaystyle{ 3 \rightarrow 4 }[/math] [math]\displaystyle{ -1,100 }[/math] [math]\displaystyle{ -800 }[/math] [math]\displaystyle{ 300 }[/math]
[math]\displaystyle{ 4 \rightarrow 1 }[/math] [math]\displaystyle{ 4,700 }[/math] ? ?
[math]\displaystyle{ 1 \rightarrow2 \rightarrow 3 \rightarrow 4 \rightarrow 1 }[/math] [math]\displaystyle{ 0 }[/math] [math]\displaystyle{ -1,400 }[/math] [math]\displaystyle{ -1,400 }[/math]
Step [[math]\displaystyle{ 2 \rightarrow 3 }[/math]]:
We now have enough information to solve for the Work done by the gas in the step in-between 2 and 3:
[math]\displaystyle{ \Delta U(23) = Q(23) + W_{on gas}(23) = Q(23) - W_{by gas}(23) }[/math]
[math]\displaystyle{ W_{by gas}(23) = Q(23) - \Delta U(23) = -3,800 + 3,400 = -400 \ J }[/math]
Step [[math]\displaystyle{ 4 \rightarrow 1 }[/math]]:
For the table to be self-consistent, the total in each column (bottom row) must equal the sum of the the other rows within that column. Thus:
[math]\displaystyle{ Q_{12341} = Q_{12} + Q_{23} + Q_{34} + Q_{41} \quad \And \quad W_{12341} = W_{12} + W_{23} + W_{34} + W_{41} }[/math]
[math]\displaystyle{ Q_{41} = Q_{12341} - (Q_{12} + Q_{23} + Q_{34}) \quad \And \quad W_{41} = W_{12341} - (W_{12} + W_{23} + W_{34}) }[/math]
[math]\displaystyle{ Q_{41} = -1,400 - (-6,200 - 3,800 - 800) = -1,400 + 10,800 = 9,400 \ J }[/math]
[math]\displaystyle{ W_{41} = -1,400 - (-6,000 - 400 + 300) = -1,400 + 6,100 = 4,700 \ J }[/math]

We have filled in the table:

Four Step Thermodynamic Cycle
Step [math]\displaystyle{ \Delta U \ (J) }[/math] [math]\displaystyle{ Q \ (J) }[/math] [math]\displaystyle{ W_{by gas} \ (J) }[/math]
[math]\displaystyle{ 1 \rightarrow 2 }[/math] [math]\displaystyle{ -200 }[/math] [math]\displaystyle{ -6,200 }[/math] [math]\displaystyle{ -6,000 }[/math]
[math]\displaystyle{ 2 \rightarrow 3 }[/math] [math]\displaystyle{ -3,400 }[/math] [math]\displaystyle{ -3,800 }[/math] [math]\displaystyle{ -400 }[/math]
[math]\displaystyle{ 3 \rightarrow 4 }[/math] [math]\displaystyle{ -1,100 }[/math] [math]\displaystyle{ -800 }[/math] [math]\displaystyle{ 300 }[/math]
[math]\displaystyle{ 4 \rightarrow 1 }[/math] [math]\displaystyle{ 4,700 }[/math] [math]\displaystyle{ 9,400 }[/math] [math]\displaystyle{ 4,700 }[/math]
[math]\displaystyle{ 1 \rightarrow2 \rightarrow 3 \rightarrow 4 \rightarrow 1 }[/math] [math]\displaystyle{ 0 }[/math] [math]\displaystyle{ -1,400 }[/math] [math]\displaystyle{ -1,400 }[/math]

Connectedness

1. How is this topic connected to something that you are interested in?

  • In physics, I've always encountered the subject of "Thermodynamics" with excitement. I always loved to deal with Temperatures and [math]\displaystyle{ mC \Delta T }[/math] is the equation that I enjoy utilizing the most. Being able to explain the mechanism of our fingers instantly turning cold as they touch the ice or in reverse, our hands warming up by simply holding a cup of hot cocoa as the flow of heat from a hotter object to colder object is inspring. Plus, there are even specific quantitative relationships that exist between the Heat, Work, and internal energy, and we are able to apply them exactly into our daily lives, thus the science of "Thermodynamics" is indeed extremely empowering!

2. How is it connected to your major?

  • I major in Chemical Engineering. There are two-semesters worth of curriculum dedicated solely to "Thermodynamics" in Chemical Engineering. The fundamental laws of Thermodynamics embody mathematical deduction to a network of equations which can be applied in all branches of science and engineering. Chemical Engineers provide solutions to a wide range of problems and, many of them have to do with calculating the Heat and Work for various physical and chemical processes. Thus, "Thermodynamics" is one of the skeletal parts of Chemical Engineering.

3. Is there an interesting industrial application?

  • Thermodynamics is relevant in the energy, transportation, petrochemical, and HVAC industries.

History

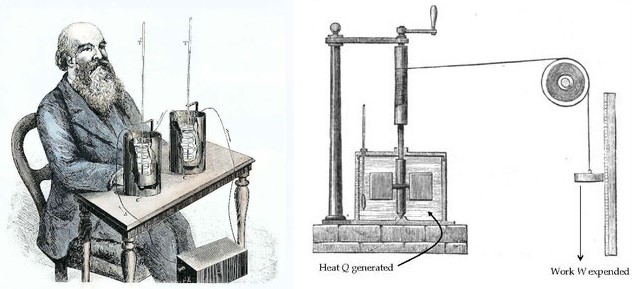
James P. Joule's experiments with Heat and Work made major contributions to the formation of the modern concept of Heat. Joule put certain amounts of mercury, water, and oil into an insulated container and mixed the liquid using a rotating stirrer. He carefully measured how much work was done by the stirrer to the liquid and the change in temperature that the liquid experienced. Joule discovered that for a particular fluid, a fixed amount of Work is required per unit mass in order to raise its Temperature by one degree. Joule established that Heat is a form of energy and that there is a quantitative relationship between Heat and Work.

The science of Thermodynamics originated in the 19th century in order to explain the mechanism of steam engines. The term 'Thermodynamics' means power developed from Heat, and Thermodynamics deals with the relationship between Heat and other forms of energy. One can apply Thermodynamics to a problem, beginning with identifying a body of matter called the system. A system's Thermodynamic state is defined by several macroscopic properties that depend on the fundamental dimensions such as time, temperature, mass, length, etc.

See also

Further reading

  • Thermodynamics (Dover Book on Physics) by Enrico Fermi
  • Engineering Thermodynamics by P. K. Nag
  • M. J. Moran and H. N. Shapiro, ‘Fundamentals of Engineering Thermodynamics’, Fourth Edition, Wiley, New York, 2000
  • Thermodynamics: An Engineering Approach by Cengel, Ya and Boles, M.A.
  • Introduction to Chemical Engineering Thermodynamics, Seventh Edition, by J.M. Smith, H.C. Van Ness, M.M. Abbott

External links

References

Retrieved from "http://www.physicsbook.gatech.edu/index.php?title=First_Law_of_Thermodynamics&oldid=36859"