Charge Density: Difference between revisions
Zmatthews3 (talk | contribs) (→Simple) |
NathanG 42 (talk | contribs) (→Simple) |
||
| (62 intermediate revisions by 2 users not shown) | |||
| Line 2: | Line 2: | ||
==The Main Idea== | ==The Main Idea== | ||
When considering the derivation of the electric field for objects extending the complexity of point charges, the concept of charge density is one that repeatedly makes an appearance. Essentially, this refers to the amount of charge per given measurement of space. Thus, because it can exist in one dimensional, two dimensional, and three dimensional forms, charge density can be represented as linear charge density, surface charge density, or volumetric charge density. | When considering the derivation of the electric field for objects extending the complexity of point charges, the concept of charge density is one that repeatedly makes an appearance. Essentially, this refers to the amount of charge per given measurement of space [http://scienceworld.wolfram.com/physics/SurfaceChargeDensity.html [2]]. Thus, because it can exist in one dimensional, two dimensional, and three dimensional forms, charge density can be represented as linear charge density, surface charge density, or volumetric charge density. | ||
For an introductory physics course, the concept of charge density is especially useful because it allows us to come up with an expression for the charge density of an infinitesimal portion of a charge distribution, which we can then use for integration over the entirety of the object in finding the overall electric field. | |||
===A Mathematical Model=== | ===A Mathematical Model=== | ||
| Line 27: | Line 29: | ||
===Simple=== | ===Simple=== | ||
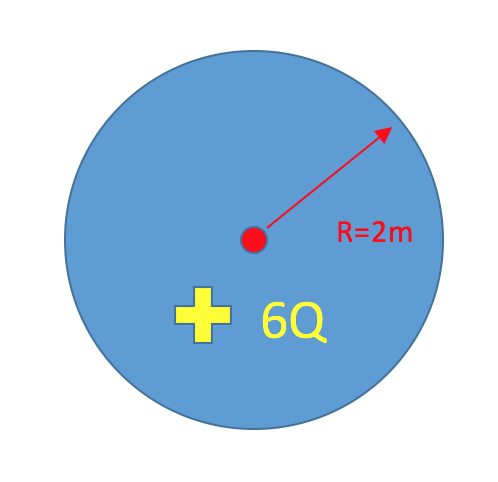
For the below rod, what is the | For the below rod, what is the surface charge density? | ||
[[File:Sphere1.png]] | [[File:Sphere1.png]] | ||
<math>\ | <math>\sigma = \frac{Q}{A} = \frac{+6Q}{\pi*(2m)^{2}} = 0.477 \frac{Q}{m^{2}} </math> | ||
===Middling=== | ===Middling=== | ||
Show that both the linear charge density and volume charge density result in the same charge for the infinitesimal portion of a charged rod. | |||
1) The charge density for an infinitesimal portion of the rod can be modeled as the linear charge density times the width of this portion: | |||
Linear charge density for the rod: <math>\lambda = \frac{Q}{L} </math> | |||
Width of infinitesimal portion: <math>dz</math> | |||
Charge density of infinitesimal portion: <math>dq = \lambda * dz = \frac{Q}{L} * dz</math> | |||
2) The charge density for an infinitesimal portion of the rod can be modeled as the volume charge density times the infinitesimal volume of this rod: | |||
Volume charge density for the rod: <math>\rho = \frac{Q}{\pi*R^{2}*L} </math> | |||
Volume of infinitesimal portion: <math>dv = \pi*R^{2} * dz </math> | |||
Charge density of infinitesimal portion: <math>dq = \rho * dv = \frac{Q}{\pi*R^{2}*L} * \pi*R^{2} * dz = \frac{Q}{L} * dz</math> | |||
Note that the result is the same for either case. | |||
===Difficult=== | ===Difficult=== | ||
Using the infinitesimal charge density of a rod, set up the integral necessary for derivation of the electric field of a ring at the center of the ring. | |||
Charge density of infinitesimal portion: <math>dq = \lambda * dz = \frac{Q}{2*\pi*R} * R*d\theta = \frac{Q}{2*\pi}*d\theta </math> | |||
Position vector between center of rod (observation location) and arbitrary infinitesimal piece in the first quadrant (source location): | |||
<math> r_{obs} - r_{source} = < 0, 0, 0> - < Rcos\theta, Rsin\theta,0> = < -Rcos\theta, -Rsin\theta,0> </math> | |||
Thus, the magnitude of the position vector is R and the unit vector = <math>< -cos\theta, -sin\theta, 0 ></math> | |||
Substituting these values into the equation for a point charge, and setting up the integral for the entirety of the sphere, we get the following: | |||
<math>\vec E = \int_0^{2\pi} \frac{1}{4\pi\epsilon_{0}}\frac{Q}{2\pi*R^{2}} < -cos\theta, -sin\theta, 0> d\theta</math> | |||
==Connectedness== | ==Connectedness== | ||
As an undergraduate research assistant, I have frequently used solenoids for control of PDMS microfluidic channels by actuating pistons. It is interesting to be able to determine the electric field in one loop of such a solenoid by using charge density. Beyond my research, solenoids have various industrial applications in the field of mechanical engineering. Examples include induction loops, medical devices, and locking mechanisms [http://www.professionaldude.com/?solenoid-applications-in-the-modern-world [4]]. | |||
==History== | ==History== | ||
Charge density first appeared in one of Maxwell's equations [http://scienceworld.wolfram.com/physics/SurfaceChargeDensity.html [1]]. The first form of these equations were published in the 1860's by James Maxwell, who sought to describe how electric and magnetic fields interact in the physical world [http://www.maxwells-equations.com/ [3]]. | |||
== See also == | == See also == | ||
Charge density can be used to derive the electric field formulas for various charge distributions. See the following for more information. | |||
[[Electric Field]] | |||
[[Charged Rod]] | |||
[[Charged Ring]] | |||
[[Charged Disk]] | |||
===Further reading=== | ===Further reading=== | ||
For a more in depth look at how charge density relates to Maxwell's equations see the following. | |||
[http://hyperphysics.phy-astr.gsu.edu/hbase/electric/diverg.html Relation of Electric Field to Charge Density] | |||
==References== | ==References== | ||
This section contains the the references you used while writing this page | This section contains the the references you used while writing this page | ||
1. [http://www.maxwells-equations.com/pho/charge-density.php http://www.maxwells-equations.com/pho/charge-density.php] | |||
2. [http://scienceworld.wolfram.com/physics/SurfaceChargeDensity.html http://scienceworld.wolfram.com/physics/SurfaceChargeDensity.html] | |||
3. [http://www.maxwells-equations.com/ http://www.maxwells-equations.com/] | |||
4. [http://www.professionaldude.com/?solenoid-applications-in-the-modern-world http://www.professionaldude.com/?solenoid-applications-in-the-modern-world] | |||
[[Category:Which Category did you place this in?]] | [[Category:Which Category did you place this in?]] | ||
Latest revision as of 08:30, 31 May 2021
Created and Claimed by Zachary Matthews
The Main Idea
When considering the derivation of the electric field for objects extending the complexity of point charges, the concept of charge density is one that repeatedly makes an appearance. Essentially, this refers to the amount of charge per given measurement of space [2]. Thus, because it can exist in one dimensional, two dimensional, and three dimensional forms, charge density can be represented as linear charge density, surface charge density, or volumetric charge density.
For an introductory physics course, the concept of charge density is especially useful because it allows us to come up with an expression for the charge density of an infinitesimal portion of a charge distribution, which we can then use for integration over the entirety of the object in finding the overall electric field.
A Mathematical Model
For each of the different types of charge density, the mathematical basis is the same, and it is quite obvious that each of the following can be related to the other two.
1) Linear charge density refers to the total amount of charge per unit length. It is modeled by the following equation:
[math]\displaystyle{ \lambda = \frac{Q}{L} }[/math]
2) Surface charge density refers to the total amount of charge per unit area. It is modeled by the following equation:
[math]\displaystyle{ \sigma = \frac{Q}{A} }[/math]
3) Volumetric charge density refers to the total amount of charge per unit volume. It is modeled by the following equation:
[math]\displaystyle{ \rho = \frac{Q}{V} }[/math]
A Computational Model
Examples
Simple
For the below rod, what is the surface charge density?
[math]\displaystyle{ \sigma = \frac{Q}{A} = \frac{+6Q}{\pi*(2m)^{2}} = 0.477 \frac{Q}{m^{2}} }[/math]
Middling
Show that both the linear charge density and volume charge density result in the same charge for the infinitesimal portion of a charged rod.
1) The charge density for an infinitesimal portion of the rod can be modeled as the linear charge density times the width of this portion:
Linear charge density for the rod: [math]\displaystyle{ \lambda = \frac{Q}{L} }[/math]
Width of infinitesimal portion: [math]\displaystyle{ dz }[/math]
Charge density of infinitesimal portion: [math]\displaystyle{ dq = \lambda * dz = \frac{Q}{L} * dz }[/math]
2) The charge density for an infinitesimal portion of the rod can be modeled as the volume charge density times the infinitesimal volume of this rod:
Volume charge density for the rod: [math]\displaystyle{ \rho = \frac{Q}{\pi*R^{2}*L} }[/math]
Volume of infinitesimal portion: [math]\displaystyle{ dv = \pi*R^{2} * dz }[/math]
Charge density of infinitesimal portion: [math]\displaystyle{ dq = \rho * dv = \frac{Q}{\pi*R^{2}*L} * \pi*R^{2} * dz = \frac{Q}{L} * dz }[/math]
Note that the result is the same for either case.
Difficult
Using the infinitesimal charge density of a rod, set up the integral necessary for derivation of the electric field of a ring at the center of the ring.
Charge density of infinitesimal portion: [math]\displaystyle{ dq = \lambda * dz = \frac{Q}{2*\pi*R} * R*d\theta = \frac{Q}{2*\pi}*d\theta }[/math]
Position vector between center of rod (observation location) and arbitrary infinitesimal piece in the first quadrant (source location):
[math]\displaystyle{ r_{obs} - r_{source} = \lt 0, 0, 0\gt - \lt Rcos\theta, Rsin\theta,0\gt = \lt -Rcos\theta, -Rsin\theta,0\gt }[/math]
Thus, the magnitude of the position vector is R and the unit vector = [math]\displaystyle{ \lt -cos\theta, -sin\theta, 0 \gt }[/math]
Substituting these values into the equation for a point charge, and setting up the integral for the entirety of the sphere, we get the following:
[math]\displaystyle{ \vec E = \int_0^{2\pi} \frac{1}{4\pi\epsilon_{0}}\frac{Q}{2\pi*R^{2}} \lt -cos\theta, -sin\theta, 0\gt d\theta }[/math]
Connectedness
As an undergraduate research assistant, I have frequently used solenoids for control of PDMS microfluidic channels by actuating pistons. It is interesting to be able to determine the electric field in one loop of such a solenoid by using charge density. Beyond my research, solenoids have various industrial applications in the field of mechanical engineering. Examples include induction loops, medical devices, and locking mechanisms [4].
History
Charge density first appeared in one of Maxwell's equations [1]. The first form of these equations were published in the 1860's by James Maxwell, who sought to describe how electric and magnetic fields interact in the physical world [3].
See also
Charge density can be used to derive the electric field formulas for various charge distributions. See the following for more information.
Further reading
For a more in depth look at how charge density relates to Maxwell's equations see the following.
Relation of Electric Field to Charge Density
References
This section contains the the references you used while writing this page
1. http://www.maxwells-equations.com/pho/charge-density.php
2. http://scienceworld.wolfram.com/physics/SurfaceChargeDensity.html
3. http://www.maxwells-equations.com/
4. http://www.professionaldude.com/?solenoid-applications-in-the-modern-world