Translational, Rotational and Vibrational Energy: Difference between revisions

From Physics Book
Jump to navigation Jump to search
 
(108 intermediate revisions by 4 users not shown)
Line 1: Line 1:
Claimed by Ferguson Beardsley Fall 2017
GABRIEL ALMEIDA SPRING 2022
 
==Main Idea==
==Main Idea==
In many cases, analyzing the kinetic energy of an object is in fact more difficult than just applying the formula <math> K = \cfrac{1}{2}mv^2 </math>. An example of this is when throwing a basketball because not only does it move through the air, but it is also rotating around its own axis. When analyzing more complicated movements like this one, it is necessary to break kinetic energy into different parts, such as rotational, translational, and vibrational, and analyze each one separately to give a more accurate picture.


In many cases, analyzing the kinetic energy of an object is in fact more difficult than just applying the formula <math> K = \cfrac{1}{2}mv^2 </math>. An example of this is when throwing a basketball because not only does it move through the air but it is also rotating around its own axis. When analyzing more complicated movements like this one, it is necessary to break kinetic energy into different parts, such as rotational, translational, and vibrational, and analyze each one separately.
Translational kinetic energy is the kinetic energy associated with the motion of the center of mass of an object. This would be the basketball traveling in the air from one location to another. While relative kinetic energy is the kinetic energy associated to the rotation or vibration of the atoms of the object around its center or axis. Relative kinetic energy would be the rotation of the basketball around it's axis. Later on this page, we go into more depth about the different types of kinetic energy.  


Here is a link to a video which explains kinetic energy in detail: [https://youtu.be/Cobhu3lgeMg]


Translational kinetic energy is the kinetic energy associated with the motion of the center of mass of an object. This would be the basketball traveling in the air from one location to another. While relative kinetic energy is the kinetic energy associated to the rotation or vibration of the atoms of the object around its center or axis. Relative kinetic energy would be the rotation of the basketball around it's axis. Later on this page, we go into more depth about the different types of kinetic energy.  
===Mathematical Model===
=== Total Kinetic Energy ===
As we just saw, the total kinetic energy of a multi particle system can be divided into the energy associated with motion of the center of mass and the motion relative to the center of mass.  
 
::<math> K_{total} = K_{translational} + K_{relative} </math>


Here is a link to a video which explains kinetic energy in detail: [https://youtu.be/Cobhu3lgeMg]
The relative kinetic energy is composed of motion due to rotation about the center of mass and vibrations/oscillations of the object.


===Kinetic Energy===
::<math> K_{total} = K_{translational} + K_{rotational} + K_{vibrational} </math>
==== Total Kinetic Energy ====
As we just saw, the total kinetic energy of a multi particle system can be divided into the energy associated with motion of the center of mass and the motion of the center of mass. [http://p3server.pa.msu.edu/coursewiki/doku.php?id=183_notes:energy_sep]


<math> K_{total} = K_{translational} + K_{relative} </math>
====Translational Kinetic Energy====


The relative kinetic energy is composed of motion due to rotation about the center of mass and vibrations/oscillations of the object.  [http://p3server.pa.msu.edu/coursewiki/doku.php?id=183_notes:energy_sep]
"Translation" means:
<math> K_{total} = K_{translational} + K_{rotational} + K_{vibrational} </math>


====Calculating Translational Kinetic Energy====
::''To move from one location to another location''


"Translation" means to move from one location to another location. By calculating translational kinetic energy, we can track how one object moves from one location to another. Since the translational kinetic energy is associated to the movement of the center of mass of the object, it is important to know how to calculate the location of the center of mass and the velocity of the center of mass which is shown in the two equations below:  
By calculating translational kinetic energy, we can track how one object moves from one location to another. Since the translational kinetic energy is associated with the movement of the center of mass of the object, it is important to know how to calculate the location of the center of mass and the velocity of the center of mass which is shown in the two equations below:  


<math> r_{CM} = \cfrac{m_1r_1 + m_2r_2+m_3r_3 + ...}{m_1 + m_2 +m_3} </math>
::<math>r_{CM} = \cfrac{m_1r_1 + m_2r_2+m_3r_3 + ...}{m_1 + m_2 +m_3}</math>
<math> v_{CM} = \cfrac{m_1v_1 + m_2v_2+m_3v_3 + ...}{m_1+ m_2 +m_3} </math>[http://p3server.pa.msu.edu/coursewiki/doku.php?id=183_notes:center_of_mass]


Here is a link to video if you want to refresh knowledge one center of mass: [https://youtu.be/5qwW8WI1gkw]
::<math>v_{CM} = \cfrac{m_1v_1 + m_2v_2+m_3v_3 + ...}{m_1+ m_2 +m_3}</math>


The motion of canter of mass is described by the velocity of center of mass. Using the total mass and the velocity of the center of mass, we :
:Here is a link to a video if you want to refresh your knowledge on center of mass: [https://youtu.be/5qwW8WI1gkw]


<math> K_{translational} = \cfrac{1}{2}M_{total}v_{CM}^2 </math>[http://p3server.pa.msu.edu/coursewiki/doku.php?id=183_notes:energy_sep]
The motion of the center of mass is described by the velocity of the center of mass. Using the total mass and the velocity of the center of mass, we define the translational kinetic energy as:


====Calculating Vibrational Kinetic Energy====
::<math>K_{translational} = \cfrac{1}{2}M_{total}v_{CM}^2</math>


The total energy due to vibrations is the sum of the potential energy associated with interaction causing the vibrations and the kinetic energy of the vibrations.  
====Vibrational Kinetic Energy====
The total energy due to vibrations is the sum of the potential energy associated with interactions causing the vibrations and the kinetic energy of the vibrations.  


<math> E_{vibrational} = K_{vibrational} +U_{s} </math>
::<math>E_{vibrational} = K_{vibrational} + U_{s}</math>


The easiest way to find vibrational kinetic energy is by knowing the other energy terms and isolating the vibrational kinetic energy:
The easiest way to find vibrational kinetic energy is by knowing the other energy terms and isolating the vibrational kinetic energy. This is when there is no rotational kinetic energy:


<math> E_{total} = K_{trans} + K_{vibrational} + U_{s} +E_{rest}</math>
::<math>E_{total} = K_{trans} + K_{vibrational} + U_{s} +E_{rest}</math>
<math> K_{vibrational} = E_{total} - (K_{trans} + U_{s} +E_{rest})</math>
::<math>K_{vibrational} = E_{total} - (K_{trans} + U_{s} +E_{rest})</math>


====Calculating Rotational Kinetic Energy====
====Rotational Kinetic Energy====
[[File:Kinetic_energy.png|300px|right|thumb|Here are links to two videos that cover rotational kinetic energy and moment of interia: [https://youtu.be/craljBk-E5g][https://youtu.be/XlFlZHfAZeE]]]
Rotational kinetic energy is the energy due to the rotation about the center of mass. It can be calculated by finding the angular momentum and inertia of the system, which will be discussed in greater detail in the next two sections. The equation used to find kinetic rotational energy is below:


Similarly, we can calculate rotational kinetic energy with the following formula:
::<math>K_{rotational} =\frac{1}{2} I_{cm}{\omega}^2</math>


<math> K_{rotational} = \cfrac{1}{2}M_{total}v_{CM}^2 </math>
Another important rotational equation is:


=====Calculating Moment of Inertia=====
::<math></math>


But rotational kinetic energy can also be calculated with the moment of inertia and the angular speed of an object. The moment of inertia of an object is the sum of the products of the mass of each particle in the object with the square of their distance from the axis of rotation. The general formula for calculating the moment of inertia of an object is:
=====Moment of Inertia=====
The moment of inertia of an object shows the difficulty of rotating an object, since the larger the moment of inertia the more energy is required to rotate the object at the same angular velocity as an object with a smaller moment of inertia. The moment of inertia of an object is defined as the sum of the products of the mass of each particle in the object with the square of their distance from the axis of rotation. The general formula for calculating the moment of inertia of an object is:


<math> I = m_1r_{\perp,1}^2 + m_2r_2{\perp,2}^2 + m_3r_{\perp,3}^2 +...</math>    <math> kg.m^2 </math>
::<math>I = m_1{r_{1}}^2 + m_2{r_{2}}^2 + m_3{r_{3}}^2 +...</math>


Here <math> r_1, r_2, r_3 </math> represent the perpendicular distance from the point/axis of rotation.
:::Here <math> r_1, r_2, r_3 </math> represent the perpendicular distance from the point/axis of rotation.
Moment of Inertia is actually calculated using Calculus. These values we obtain for standard objects are not once you will need to derive, but conceptually understanding how they come to be will help you understand Moment of Inertia and it's impact on a solid.


The reason we use density in the the calculations is because for uniform solids density is constant throughout the material, implying it has even mass distribution.
:or


[[File:MomentOfInertiaRod1.jpg]]
::<math>I = \sum_{i} m_{i}{r_{i}}^2</math>
[[File:MomentOfInertiaRod2.jpg]]
[[File:MomentOfInertiaCylinder1.jpg]]
[[File:MomentOfInertiaCylinder2.jpg]]


This is to give you an intuitive idea about how Moment of Inertia is calculated, not that you will have to. But an interesting thing it tells you is that when you compare two bodies rotating with the same kinetic energy and one of them has a higher moment of Inertia, then the one with the higher moment of Inertia has a lower speed since <math> w </> must be lower. If <math> w </math> is lower and radius is higher that means mass must be low since Moment of Inertia also depends on mass and distance from axis of rotation. So we can deduce such relations which helps us understand how the moment of Inertia of an object actually affects the object in different ways.
:For a body with a uniform distribution of mass this can be turned into an integral:


Use this to try and derive the Moment Of Inertia for some other objects you know. ( Sphere is a little challenging )
::<math>I = \int r^2 \ dm</math>


[[File:MomentOfInert.jpg]]
The units of rotational inertia are <math> kg \cdot m^2 </math>
[[File:MomentOfInert22.jpg]]


===== Angular Speed =====
[[File:4c906c92cebe30d9486deb2a682acf561d23c9c1.png|900px|center]]


The angular speed is a calculation of how fast the object is rotating. It can be calculated from the period, T, with the following formula : <math> \omega = \cfrac{2\pi}{T} </math>
=====Angular Speed and Acceleration=====
The angular speed is the rate at which the object is rotating. It is given in the following formula:
[[File:Angularvelocity.png|right|200px]]


The rotational kinetic energy can thus be calculated using these two variables: <math> K_{rotational} = \cfrac{1}{2}I\omega^2 </math>.
::<math>\omega = \cfrac{2\pi}{T}</math>, where


==== Point Particle System VS Extended System ====
:::<math>T =</math> the period of the rotation


Why is it useful to divide the kinetic energy into two different elements? When calculating the total energy of a system, depending on how it is modeled, it will contain one or more types of kinetic energies. Let's think about a system modeled as a point particle system. In this model of a system, we think of the object as one point, located at its center of mass. With this way of thinking, it becomes clear that there can only be one type of kinetic energy: translational kinetic energy. There cannot be any rotational kinetic energy because there are no atoms rotating about the center of mass, since we are thinking of the center of mass as the entire object. Our general energy equation thus boils down to this:
The angle in which a disk turns is <math>2 \pi</math> in a time <math>T</math>. It is measured in radians per second. The tangential velocity of an object is related to its radius r at the angular speed because the tangential velocity increases when the distance from the center of an object increases. It is shown in the equation below:


<math> \triangle E_{system} = W </math> where <math> W =  F_{net} . \triangle r_{CM} </math> and <math> \triangle E_{system} = \triangle K_{translational} </math> since there is only translational kinetic energy.
::<math>v(r)= \omega r</math>


We end up with <math> \triangle K_{translational} = F_{net} . \triangle r_{CM} </math>
The angular acceleration a rotating object goes through to change its angular speed is given by:


Note: There may also be spring potential energy and rest energy depending on the example.
::<math>a(r) = \alpha r</math>


===Computational Model===
Here is a rotating rod computational model example:


Therefore, viewing a system as a point particle system allows us to easily calculate the translational kinetic energy. This translational kinetic energy will be the same in the extended system.
https://trinket.io/glowscript/31d0f9ad9e


After having calculated the translational kinetic energy of the system using the point particle system, we can use this value to calculate other terms in the general equation in the extended system.
==Examples==


We start with the general energy equation:
===Simple===
<math> \triangle E_{system} = W </math> where <math> W = F_{net} . displacement </math>


A player throws a mid-court pass horizontally with a <math>624g</math> basketball. This pass covers <math>15 \ m</math> in <math>2 \ s</math>.


In this extended system, we consider all the atoms and their rotation about the axis as well as the general movement of the center of mass. We end up with
:'''a) What is the basketball’s average translational kinetic energy while in flight?
<math> \triangle K_{translational} + \triangle K_{rotational} + \triangle K_{vibrational} = F_{net} . displacement </math>


::Since the ball is moving relative to the gym, we can describe its average velocity, and thus translational kinetic energy as:


Note: Here again, there may be spring potential energy and rest energy included in this equation depending on the example.
:::<math>v_{avg} = \frac{d}{t} = \frac{15}{2} = 7.5 \ \frac{m}{s}</math>


===A Computational Model===
:::<math>K_{avg_{b}} = \frac{1}{2}m{v_{avg}}^2 = \frac{1}{2} \times 0.624 \times (7.5)^2 = 17.55 \ J</math>
==== Vpython ====
There are not many applications of vpython for this chapter because it necessitates such a conceptual way of thinking. However, it is possible to make a program that calculates the rotational energy given displacements for each force and the magnitude of the force. The mass of the object and the initial conditions would have to be given as well.


====Visualizing translational and rotational kinetic energy ====
An average molecule of air in the basketball, has a mass of <math>29 \ u</math>, and an average speed of <math>500 \ \frac{m}{s}</math>, relative to the basketball. There are about <math>3 \times 10^{23}</math> molecules inside it, moving in random directions, when the ball is properly inflated.
It is important to really think about translational kinetic energy as the movement of the center of mass and only that. In the point particle system, only translational kinetic energy is present because we are visualizing the object only as its center of mass, and that is therefore the only kind of movement we have. Let's take the earth as an example. The earth rotates around itself, as well as around the sun. If you think of the earth only in terms of its center of mass, you realize that the center of mass only has one kind of movement: around the sun. It is useful to think of the earth in this case, the point particle system, as a dot, located at its center of mass.


[[File:Wiki 5.gif|center]]
:'''b) What is the average translational kinetic energy of the random motion of all the molecules inside, relative to the basketball?


In the extended system, however, we consider the movement of the center of mass as well as the movement of all the atoms around it. Since the atoms of the earth that are not its center rotate (one rotation every 24h), there is rotational energy. Its center of mass is still moving around the sun, there is therefore also translational energy. Here, we think of the earth as a sphere, not a dot, in which the atoms rotate about an axis or center.
::Since the average speed of a molecule is <math>500 \ \frac{m}{s}</math>, we can calculate the average translational kinetic energy of a given molecule:


[[File:Wiki 7.jpeg|center]]
:::<math>K_{avg_{g}} = \frac{1}{2}m_{g}{v_{avg_{g}}}^2</math>


For another visual approach of this concept, you can watch the following video: https://www.youtube.com/watch?v=zDcf7eEaP0M.
::The mass of a molecule in kilograms <math>(m_{g})</math> will be the atomic mass <math>(m_{A})</math> times a conversion factor <math>(A)</math>:


==Examples==
:::<math>m_{g} = m_{A}A = 29 \times 1.66 \times 10^{-27} = 4.814 \times 10^{-26} \ kg</math>


===Simple===
::Thus, the translational kinetic energy of an average molecule relative to the ball is:
''Problem statement'':


Calculate the rotational kinetic energy of a wheel of radius 100cm, mass 10kg, with and angular velocity of 22 radians/s.
:::<math>K_{avg_{g}} = \frac{1}{2}m_{g}{v_{avg_{g}}}^2 = \frac{1}{2} \times 4.814 \times 10^{-26} \times (500)^2 = 6.0175 \times 10^{-21} \ J</math>


::Multiplying this kinetic energy by the number of molecules will give us our answer:


''Solution'':
:::<math>K_{avg_{total}} = N K_{avg_{g}} = 3 \times 10^{23} \times 6.0175 \times 10^{-21} = 1,805.25 \ J</math>


We know how to calculate the moment of inertia for a disk, and the moment of inertia for a wheel will  be the same since all the atoms are at the same distance from the center. Therefore, <math> I = MR^2 = (10)(1)^2 = 10  kgm^2 </math>
::The kinetic energy possessed by the gas relative to the ball is <math>1,805.25</math> Joules.


From there, we can easily calculate the rotational kinetic energy:
:'''c) How fast would the basketball have to travel relative to the court to have a kinetic energy equal to the amount in part (b)?
<math> K_{rotational} = \cfrac{1}{2}I\omega^2 = \cfrac{1}{2}(10)(22)^2 = 2420 </math> Joules


===Middling===
::The basketball would have to have a translational kinetic energy equal to <math>1,805.25</math> Joules. To do this the ball's speed would have to satisfy:
''Problem statement'':


A string is wrapped around a disk of radius 0.15m and mass 3kg. The disk is initially at rest, but you pull the string with a force of 10N along a smooth surface. The disk moves a distance d = 0.1m and your hand pulls through a distance h = 0.2m. What is the speed of the center of mass of the disk after having pulled the string?
:::<math>K_{ball} = \frac{1}{2}m_{ball}v^2</math>


[[File:Wiki 2.png|center]]
::Solving for <math>v</math> gives:


''Solution'':
:::<math>v = \sqrt{\frac{2K_{ball}}{m_{ball}}} = \sqrt{\frac{2 \times 1,805.25}{0.624}} = 76.07 \ \frac{m}{s}</math>


The problem states that the disk is moving on a smooth surface, so there is no friction here. Since the problem asks about the speed of the center of mass, we will consider the point particle system first. We start with:
===Middling===


<math> \triangle K_{translational} = F_{net} . \triangle r_{CM} </math>  
A wheel is mounted on a stationary axel, which is nearly frictionless so that the wheel turns freely. The wheel has an inner ring with a mass of <math>5 \ kg</math> and a radius of <math>10 \ cm</math>, and an outer ring with a mass of <math>2 \ kg</math> and a radius of <math>25 \ cm</math>; the spokes have negligible mass. A string with negligible mass is wrapped around the outer ring and you pull on it, increasing the rotational speed of the wheel.


We know that the translational kinetic energy is <math> K = \cfrac{1}{2}mv_{CM}^2 </math>
:'''a) During the time that the wheel's rotation changes from 4 revolutions per second to 7 revolutions per second, how much work do you do?'''


So we end up with:
::To find the work done, the best course of action will be to find the change in kinetic energy of the wheel. To do this, we will need to find the change in angular speed and the moment of inertia of the wheel.


<math> \cfrac{1}{2}mv_{CM,f}^2 - \cfrac{1}{2}mv_{CM,i}^2 = F_{net} . \triangle r_{CM} </math>
::We are given the initial and final frequencies of rotation for the wheel:


Because initially the disk is still, we can reduce this equation to:
:::<math>f_{0} = 4 \ s^{-1} \quad \And \quad f_{f} = 7 \ s^{-1}</math>


<math> \cfrac{1}{2}mv_{CM,f}^2 = F_{net} . \triangle r_{CM} </math>
::The frequency of a rotation is related to its period by:


<math> v_{CM,f}^2 = \cfrac{2. F_{net} . \triangle r_{CM}}{m} </math>
:::<math>T = \frac{1}{f}</math>


<math> v_{CM,f} = \sqrt{\cfrac{2. F_{net} . \triangle r_{CM}}{m}} </math>
::Therefore, we have the initial and final period of rotation:


<math> v_{CM,f} = \sqrt{\cfrac{ (2)(10)(0.1)}{3}} </math>
:::<math>T_{0} = \frac{1}{f_{0}} = \frac{1}{4} = 0.25 \ s \quad \And \quad T_{f} = \frac{1}{f_{f}} = \frac{1}{7} = 0.1429 \ s</math>


<math> v_{CM,f} =  0.816 </math> m/s
::The period of a rotation is related to the body's angular speed by:
===Difficult===
''Problem statement''


A box contains a machinery that can rotate. The mass of the box and what it contains is 10kg. A string is wound around the machinery inside the box and comes out of a hole at the top of the box. Before you pull the string, the machinery is not rotating and the box is sitting still. You then pull 0.9m of string out of the box with a force F = 100N and the box lifts up a distance of 0.2m. What is the rotational Kinetic energy of the mechanism inside the box?
:::<math>T = \frac{2\pi}{\omega} \quad \therefore \quad \omega = \frac{2\pi}{T}</math>


[[File:wiki 6.png|center]]
::Therefore, we can calculate the initial and final angular speeds of the wheel:


''Solution''
:::<math>\omega_{0} = \frac{2\pi}{T_{0}} = \frac{2\pi}{0.25} = 25.133 \ \left(\frac{rads}{s}\right) \quad \And \quad \omega_{f} = \frac{2\pi}{T_{f}} = \frac{2\pi}{0.1429} = 43.969 \ \left(\frac{rads}{s}\right)</math>


We cannot calculate the rotational energy directly because we do not have any indication of the shape of the mechanism and its angular speed. Therefore, we will use the point particle system and the extended system to find this value. Begin by finding the value of the translational kinetic energy of the system by using the point particle model.
::Now, to find the moment of inertia, we assume the separate rings are thin enough to use the moment of inertia for a thin ring, from the table above:
We have:


<math> \triangle K_{translational} = F_{net} . \triangle r_{CM} </math>
:::<math>I = mr^2</math>
<math> K_{translational,f} - K_{translational,i} =  F_{net} . \triangle r_{CM} </math>


The initial translational kinetic energy is 0 because the center of mass of the object is not moving initially.
::However, since there are two concentric rings that make up the wheel (ignoring the spokes), we must add their moments of inertia to calculate the total moment of inertia for the wheel:


<math> K_{translational,f} = F_{net} . \triangle r_{CM} </math>
:::<math>I_{wheel} = I_{inner} + I_{outer} = m_{inner} r^2_{inner} + m_{outer} {r}^2_{outer} = 5 \times (0.1)^2 + 2 \times (0.25)^2 = 0.175 \ (kg \cdot m^2)</math>


<math> K_{translational,f} = (F_{hand} - F_{grav}) (0.2) </math>
::Using the Energy Principle, and assuming the only work done on the wheel is due to the string being pulled, we can say:


<math> K_{translational,f} = (114 - mg) (0.2) </math>
:::<math>\Delta E_{wheel} = W_{on wheel}</math>


<math> K_{translational,f} = (114 - (10)(9.8)) (0.2) </math>
:::<math>\Delta U_{wheel} + \Delta K_{transalational_{wheel}} + \Delta K_{rotational_{wheel}} = W_{on wheel} \quad \And \quad \Delta U_{wheel} = 0 \quad \And \quad \Delta K_{translational_{wheel}} = 0</math>


<math> K_{translational,f} = 3.2 </math> Joules
:::<math>\Delta K_{rotational_{wheel}} = W_{wheel}</math>


Now let's look at the extended system:
::The rotational kinetic energy of the wheel is given by:


Here, we have:
:::<math>K_{rotational} = \frac{1}{2} I_{wheel} \omega_{wheel}</math>


<math> \triangle K_{translational} + \triangle K_{rotational} = F_{net} . displacement </math>
::Thus, the change in rotational kinetic energy of the wheel will be:


Since there is no initial translational or rotational kinetic energy, we get:
:::<math>\Delta K_{r} = \frac{1}{2} I_{wheel} (\omega^2_{f} - \omega^2_0) = \frac{1}{2} \times 0.175 \times ((43.969)^2 - (25.133)^2) = 113.89 \ J</math>


<math> K_{translational,f} + K_{rotational,f} = F_{net} . displacement </math>
::Since we are assuming there is no friction in this process and the center of mass of the wheel does not move, all the work done is due to you pulling the string:


<math> K_{rotational,f} = F_{net} . displacement - K_{translational} </math>
:::<math>W_{you} = \Delta K_{r} = 113.89 \ J</math>


The gravitational force mg acts through the distance that the center of mass of the box moves, while the force of your hand acts through that distance plus the distance the string uncoils. Therefore, we have:


<math> K_{rotational,f} = (114)(0.2 + 0.9) - (10)(9.8)(0.2) - 3.2 </math>
===Difficult===
Image: https://drive.google.com/file/d/185xWvF0iMpX-dUNc91ZOhCxQIq7-hHM3/preview


<math> K_{rotational,f} =  102.6 </math> Joules


==Connectedness==
#How is this topic connected to something that you are interested in?
In the book, this topic is very much related to sports. It uses countless examples from diving, ice skating or frisbee to demonstrate why kinetic energy can be separated into two terms. I have always been interested in sports and they were always a big part of my life. Therefore when I read the book, this was one of the most interesting sections to me because I felt some kind of connection to it, like it applied to my life, since I had ice-skated and dove when I was young.


##How is it connected to your major?
A common flywheel design is a flattened disk (cylinder) rotating about an axis perpendicular to its center, as shown in the figure. Let’s assume our cylinder is about a meter across ( R = 0.5 m ) and has a mass of 240 kg (i.e. has a weight of about 530 pounds). The moment of inertia for such a shape is <math> I = (1/2)MR^2 </math>. What velocity do I need the disk to rotate in order to power a house? A typical home uses energy at a rate of roughly 1000 W or 1000 J/s.    
Some biomedical engineers go on to work with sports stars on smart clothes or even prosthetics, in which case they have to deal with rotation and vibration, in addition to regular kinetic energy. The study of biomechanics largely relies on physics as well.


###Is there an interesting industrial application?
There are many developments of machines that will use kinetic energy for power. We may very well see a few years from now a shoe on the market that powers your cell phone or any other type of technology. There are many possibilities for advancements such as this one.


==History==


Kinetic energy was first set apart from potential energy by Aristotle. However, it wasn't until 1929 that Gaspard-Gustave Coriolis showed the first signs of understanding of kinetic energy the way that we do today. The term was later coined by William Thomson.
<math> I = (0.5)*(240)*(0.5)^2 = 30 Kg*m^2 </math>


== See also ==
Energy consumption in a day:


For more specific information on point particle systems and extended systems:
<math> E{k} = 1000 * 24* 3600 = 8.64 * 10^7 J </math>
http://www.physicsbook.gatech.edu/Point_Particle_Systems ;
http://www.physicsbook.gatech.edu/Real_Systems


For more specific information on the conservation of energy:
<math> E = (1 / 2)Iw^2 </math>
http://www.physicsbook.gatech.edu/Conservation_of_Energy


For more information on potential energy and when it is present:
Energy = angular times inertia:
http://www.physicsbook.gatech.edu/Potential_Energy


For information on how to take this concept further to calculate thermal energy in some instances:
<math> w = √(2E/I) </math>
http://www.physicsbook.gatech.edu/Thermal_Energy
<math> w = √(2*8.64*10^7/30) = 2400 rad/sec </math>
<math> v = r*w = 0.5 * 2400 = 1200 m/sec </math>


===Further reading===
==Connectedness==
'''1. How is this topic connected to something that you are interested in?'''


Matter and Interactions By Ruth W. Chabay, Bruce A. Sherwood - Chapter 9
*This topic connected to me because I used to dance when I was younger. This section focused on kinetic energy and the different parts of kinetic energy. You could break up different parts of dance and compare it to kinetic energy.


http://www.scienceclarified.com/everyday/Real-Life-Physics-Vol-2/Energy-Real-life-applications.html
*This topic resonated with my tennis experience. If you play tennis there are certain moves that generate specific rotations patterns on the ball and can either increase or decrease the length of its trajectory. Top spin, for example, involves spinning the ball forward and this leads to a positive change in K{rot} and, if we assume no change in K{trans}, an increase in K{total} that extends the ball's trajectory.


http://spie.org/x48868.xml
'''2. How is it connected to your major?'''


===External links===
*In Chemical Engineering, we will focus on the kinetic energy on the microscopic level and determining the energy of the particles by looking at the translational, rotational, and vibrational energies of the atom, and how they allow chemical reactions to precess.


http://hyperphysics.phy-astr.gsu.edu/hbase/rke.html
'''3. Is there an interesting industrial application?'''


http://www.sparknotes.com/physics/rotationalmotion/rotationaldynamics/section3.rhtml
*There are many machines that use kinetic energy for power, and we will probably see in a few years from now the use of rotational, translational, and vibrational energy to power anything from phones to computers.


http://hyperphysics.phy-astr.gsu.edu/hbase/rotwe.html
==History==
Kinetic energy was first set apart from potential energy by Aristotle. Later, in the 1600's, Leibniz and Bernoulli developed the idea that <math>E \propto mv^2</math>, and they called it the 'living force.' However, it wasn't until 1829 that Gaspard-Gustave Coriolis showed the first signs of understanding kinetic energy the way that we do today by focusing on the transfer on energy in rotating water wheels. Finally, in 1849, Lord Kelvin is said to have coined the term 'kinetic energy.'


http://classroom.synonym.com/kinetic-energy-potential-energy-apply-everyday-life-15430.html
==See also==


==References==
===Further Reading===
*[[Point Particle Systems]]<br>
*[[Real Systems]]<br>
*[[Conservation of Energy]]<br>
*[[Potential Energy]]<br>
*[[Thermal Energy]]<br>
*[[Internal Energy]]<br>
*[[Center of Mass]]<br>


All images used on this page do not belong to me.  
===External Links===
All problem examples are from the Matter and Interactions Physics book referenced below.
*https://www.youtube.com/watch?v=5qwW8WI1gkw&feature=youtu.be<br>
*https://youtu.be/Cobhu3lgeMg<br>
*https://www.youtube.com/watch?v=craljBk-E5g&feature=youtu.be<br>
*https://youtu.be/XlFlZHfAZeE<br>
*https://youtu.be/vL5yTCyRMGk<br>
*https://en.wikipedia.org/wiki/Kinetic_energy<br>
*https://en.wikipedia.org/wiki/Moment_of_inertia<br>
*https://www.khanacademy.org/science/physics/torque-angular-momentum/torque-tutorial/a/rotational-inertia<br>
*https://youtu.be/vL5yTCyRMGk


https://en.wikipedia.org/wiki/Kinetic_energy#History_and_etymology
==References==
All problem examples, youtube videos, and images are from the websites referenced below:


http://www.murderati.com/category/stephen-jay-schwartz/
*http://www.robjorstad.com/Phys161/161Lab/161RotationalKinematicsSim.pdf


http://learning.alfriston.bucks.sch.uk/course/view.php?id=47
*http://p3server.pa.msu.edu/coursewiki/doku.php?id=183_notes:energy_sep


http://www.school-for-champions.com/astronomy/earth_motion.htm#.Vloe4HarSM8
*https://cnx.org/contents/1Q9uMg_a@6.4:V7Fr-AEP@3/103-Relating-Angular-and-Trans


Matter and Interactions By Ruth W. Chabay, Bruce A. Sherwood - Chapter 9
*https://en.wikipedia.org/wiki/Gaspard-Gustave_de_Coriolis


[[Category:Energy]]
*https://newton.ph.msstate.edu/fox/public_html/ph2213/examples10-core.pdf

Latest revision as of 12:21, 18 April 2022

GABRIEL ALMEIDA SPRING 2022

Main Idea

In many cases, analyzing the kinetic energy of an object is in fact more difficult than just applying the formula [math]\displaystyle{ K = \cfrac{1}{2}mv^2 }[/math]. An example of this is when throwing a basketball because not only does it move through the air, but it is also rotating around its own axis. When analyzing more complicated movements like this one, it is necessary to break kinetic energy into different parts, such as rotational, translational, and vibrational, and analyze each one separately to give a more accurate picture.

Translational kinetic energy is the kinetic energy associated with the motion of the center of mass of an object. This would be the basketball traveling in the air from one location to another. While relative kinetic energy is the kinetic energy associated to the rotation or vibration of the atoms of the object around its center or axis. Relative kinetic energy would be the rotation of the basketball around it's axis. Later on this page, we go into more depth about the different types of kinetic energy.

Here is a link to a video which explains kinetic energy in detail: [3]

Mathematical Model

Total Kinetic Energy

As we just saw, the total kinetic energy of a multi particle system can be divided into the energy associated with motion of the center of mass and the motion relative to the center of mass.

[math]\displaystyle{ K_{total} = K_{translational} + K_{relative} }[/math]

The relative kinetic energy is composed of motion due to rotation about the center of mass and vibrations/oscillations of the object.

[math]\displaystyle{ K_{total} = K_{translational} + K_{rotational} + K_{vibrational} }[/math]

Translational Kinetic Energy

"Translation" means:

To move from one location to another location

By calculating translational kinetic energy, we can track how one object moves from one location to another. Since the translational kinetic energy is associated with the movement of the center of mass of the object, it is important to know how to calculate the location of the center of mass and the velocity of the center of mass which is shown in the two equations below:

[math]\displaystyle{ r_{CM} = \cfrac{m_1r_1 + m_2r_2+m_3r_3 + ...}{m_1 + m_2 +m_3} }[/math]
[math]\displaystyle{ v_{CM} = \cfrac{m_1v_1 + m_2v_2+m_3v_3 + ...}{m_1+ m_2 +m_3} }[/math]
Here is a link to a video if you want to refresh your knowledge on center of mass: [4]

The motion of the center of mass is described by the velocity of the center of mass. Using the total mass and the velocity of the center of mass, we define the translational kinetic energy as:

[math]\displaystyle{ K_{translational} = \cfrac{1}{2}M_{total}v_{CM}^2 }[/math]

Vibrational Kinetic Energy

The total energy due to vibrations is the sum of the potential energy associated with interactions causing the vibrations and the kinetic energy of the vibrations.

[math]\displaystyle{ E_{vibrational} = K_{vibrational} + U_{s} }[/math]

The easiest way to find vibrational kinetic energy is by knowing the other energy terms and isolating the vibrational kinetic energy. This is when there is no rotational kinetic energy:

[math]\displaystyle{ E_{total} = K_{trans} + K_{vibrational} + U_{s} +E_{rest} }[/math]
[math]\displaystyle{ K_{vibrational} = E_{total} - (K_{trans} + U_{s} +E_{rest}) }[/math]

Rotational Kinetic Energy

Here are links to two videos that cover rotational kinetic energy and moment of interia: [1][2]

Rotational kinetic energy is the energy due to the rotation about the center of mass. It can be calculated by finding the angular momentum and inertia of the system, which will be discussed in greater detail in the next two sections. The equation used to find kinetic rotational energy is below:

[math]\displaystyle{ K_{rotational} =\frac{1}{2} I_{cm}{\omega}^2 }[/math]

Another important rotational equation is:

[math]\displaystyle{ }[/math]
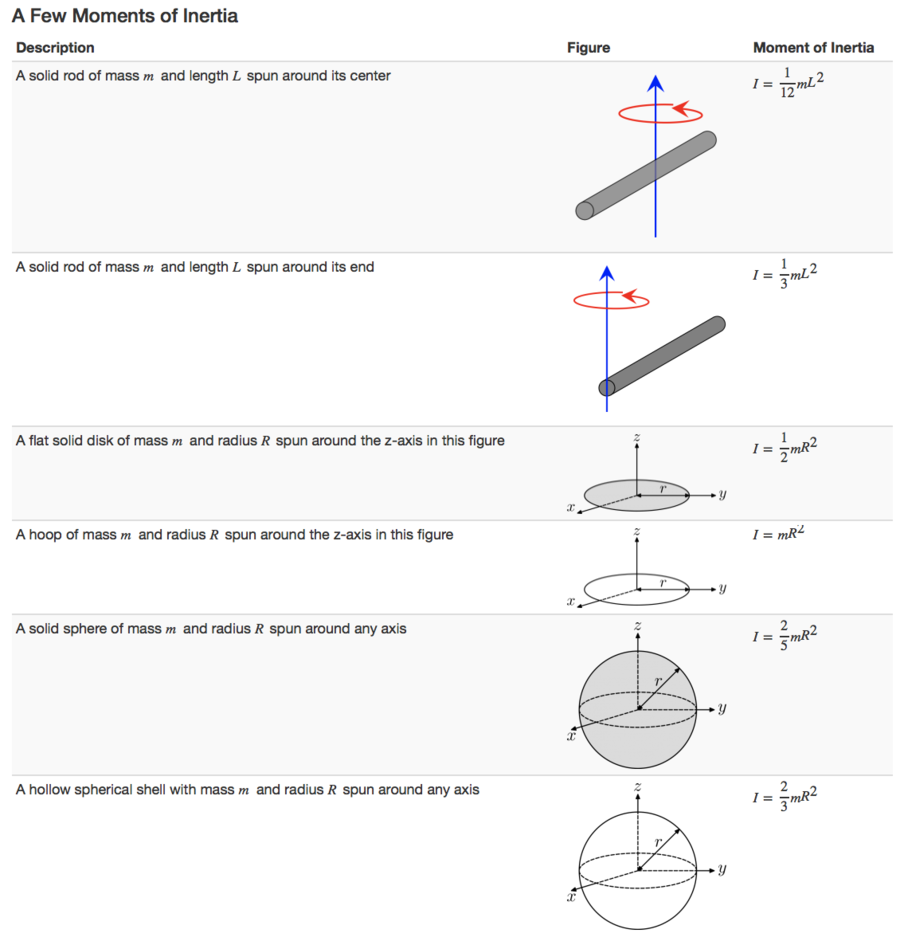
Moment of Inertia

The moment of inertia of an object shows the difficulty of rotating an object, since the larger the moment of inertia the more energy is required to rotate the object at the same angular velocity as an object with a smaller moment of inertia. The moment of inertia of an object is defined as the sum of the products of the mass of each particle in the object with the square of their distance from the axis of rotation. The general formula for calculating the moment of inertia of an object is:

[math]\displaystyle{ I = m_1{r_{1}}^2 + m_2{r_{2}}^2 + m_3{r_{3}}^2 +... }[/math]
Here [math]\displaystyle{ r_1, r_2, r_3 }[/math] represent the perpendicular distance from the point/axis of rotation.
or
[math]\displaystyle{ I = \sum_{i} m_{i}{r_{i}}^2 }[/math]
For a body with a uniform distribution of mass this can be turned into an integral:
[math]\displaystyle{ I = \int r^2 \ dm }[/math]

The units of rotational inertia are [math]\displaystyle{ kg \cdot m^2 }[/math]

Angular Speed and Acceleration

The angular speed is the rate at which the object is rotating. It is given in the following formula:

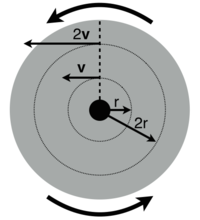
[math]\displaystyle{ \omega = \cfrac{2\pi}{T} }[/math], where
[math]\displaystyle{ T = }[/math] the period of the rotation

The angle in which a disk turns is [math]\displaystyle{ 2 \pi }[/math] in a time [math]\displaystyle{ T }[/math]. It is measured in radians per second. The tangential velocity of an object is related to its radius r at the angular speed because the tangential velocity increases when the distance from the center of an object increases. It is shown in the equation below:

[math]\displaystyle{ v(r)= \omega r }[/math]

The angular acceleration a rotating object goes through to change its angular speed is given by:

[math]\displaystyle{ a(r) = \alpha r }[/math]

Computational Model

Here is a rotating rod computational model example:

https://trinket.io/glowscript/31d0f9ad9e

Examples

Simple

A player throws a mid-court pass horizontally with a [math]\displaystyle{ 624g }[/math] basketball. This pass covers [math]\displaystyle{ 15 \ m }[/math] in [math]\displaystyle{ 2 \ s }[/math].

a) What is the basketball’s average translational kinetic energy while in flight?
Since the ball is moving relative to the gym, we can describe its average velocity, and thus translational kinetic energy as:
[math]\displaystyle{ v_{avg} = \frac{d}{t} = \frac{15}{2} = 7.5 \ \frac{m}{s} }[/math]
[math]\displaystyle{ K_{avg_{b}} = \frac{1}{2}m{v_{avg}}^2 = \frac{1}{2} \times 0.624 \times (7.5)^2 = 17.55 \ J }[/math]

An average molecule of air in the basketball, has a mass of [math]\displaystyle{ 29 \ u }[/math], and an average speed of [math]\displaystyle{ 500 \ \frac{m}{s} }[/math], relative to the basketball. There are about [math]\displaystyle{ 3 \times 10^{23} }[/math] molecules inside it, moving in random directions, when the ball is properly inflated.

b) What is the average translational kinetic energy of the random motion of all the molecules inside, relative to the basketball?
Since the average speed of a molecule is [math]\displaystyle{ 500 \ \frac{m}{s} }[/math], we can calculate the average translational kinetic energy of a given molecule:
[math]\displaystyle{ K_{avg_{g}} = \frac{1}{2}m_{g}{v_{avg_{g}}}^2 }[/math]
The mass of a molecule in kilograms [math]\displaystyle{ (m_{g}) }[/math] will be the atomic mass [math]\displaystyle{ (m_{A}) }[/math] times a conversion factor [math]\displaystyle{ (A) }[/math]:
[math]\displaystyle{ m_{g} = m_{A}A = 29 \times 1.66 \times 10^{-27} = 4.814 \times 10^{-26} \ kg }[/math]
Thus, the translational kinetic energy of an average molecule relative to the ball is:
[math]\displaystyle{ K_{avg_{g}} = \frac{1}{2}m_{g}{v_{avg_{g}}}^2 = \frac{1}{2} \times 4.814 \times 10^{-26} \times (500)^2 = 6.0175 \times 10^{-21} \ J }[/math]
Multiplying this kinetic energy by the number of molecules will give us our answer:
[math]\displaystyle{ K_{avg_{total}} = N K_{avg_{g}} = 3 \times 10^{23} \times 6.0175 \times 10^{-21} = 1,805.25 \ J }[/math]
The kinetic energy possessed by the gas relative to the ball is [math]\displaystyle{ 1,805.25 }[/math] Joules.
c) How fast would the basketball have to travel relative to the court to have a kinetic energy equal to the amount in part (b)?
The basketball would have to have a translational kinetic energy equal to [math]\displaystyle{ 1,805.25 }[/math] Joules. To do this the ball's speed would have to satisfy:
[math]\displaystyle{ K_{ball} = \frac{1}{2}m_{ball}v^2 }[/math]
Solving for [math]\displaystyle{ v }[/math] gives:
[math]\displaystyle{ v = \sqrt{\frac{2K_{ball}}{m_{ball}}} = \sqrt{\frac{2 \times 1,805.25}{0.624}} = 76.07 \ \frac{m}{s} }[/math]

Middling

A wheel is mounted on a stationary axel, which is nearly frictionless so that the wheel turns freely. The wheel has an inner ring with a mass of [math]\displaystyle{ 5 \ kg }[/math] and a radius of [math]\displaystyle{ 10 \ cm }[/math], and an outer ring with a mass of [math]\displaystyle{ 2 \ kg }[/math] and a radius of [math]\displaystyle{ 25 \ cm }[/math]; the spokes have negligible mass. A string with negligible mass is wrapped around the outer ring and you pull on it, increasing the rotational speed of the wheel.

a) During the time that the wheel's rotation changes from 4 revolutions per second to 7 revolutions per second, how much work do you do?
To find the work done, the best course of action will be to find the change in kinetic energy of the wheel. To do this, we will need to find the change in angular speed and the moment of inertia of the wheel.
We are given the initial and final frequencies of rotation for the wheel:
[math]\displaystyle{ f_{0} = 4 \ s^{-1} \quad \And \quad f_{f} = 7 \ s^{-1} }[/math]
The frequency of a rotation is related to its period by:
[math]\displaystyle{ T = \frac{1}{f} }[/math]
Therefore, we have the initial and final period of rotation:
[math]\displaystyle{ T_{0} = \frac{1}{f_{0}} = \frac{1}{4} = 0.25 \ s \quad \And \quad T_{f} = \frac{1}{f_{f}} = \frac{1}{7} = 0.1429 \ s }[/math]
The period of a rotation is related to the body's angular speed by:
[math]\displaystyle{ T = \frac{2\pi}{\omega} \quad \therefore \quad \omega = \frac{2\pi}{T} }[/math]
Therefore, we can calculate the initial and final angular speeds of the wheel:
[math]\displaystyle{ \omega_{0} = \frac{2\pi}{T_{0}} = \frac{2\pi}{0.25} = 25.133 \ \left(\frac{rads}{s}\right) \quad \And \quad \omega_{f} = \frac{2\pi}{T_{f}} = \frac{2\pi}{0.1429} = 43.969 \ \left(\frac{rads}{s}\right) }[/math]
Now, to find the moment of inertia, we assume the separate rings are thin enough to use the moment of inertia for a thin ring, from the table above:
[math]\displaystyle{ I = mr^2 }[/math]
However, since there are two concentric rings that make up the wheel (ignoring the spokes), we must add their moments of inertia to calculate the total moment of inertia for the wheel:
[math]\displaystyle{ I_{wheel} = I_{inner} + I_{outer} = m_{inner} r^2_{inner} + m_{outer} {r}^2_{outer} = 5 \times (0.1)^2 + 2 \times (0.25)^2 = 0.175 \ (kg \cdot m^2) }[/math]
Using the Energy Principle, and assuming the only work done on the wheel is due to the string being pulled, we can say:
[math]\displaystyle{ \Delta E_{wheel} = W_{on wheel} }[/math]
[math]\displaystyle{ \Delta U_{wheel} + \Delta K_{transalational_{wheel}} + \Delta K_{rotational_{wheel}} = W_{on wheel} \quad \And \quad \Delta U_{wheel} = 0 \quad \And \quad \Delta K_{translational_{wheel}} = 0 }[/math]
[math]\displaystyle{ \Delta K_{rotational_{wheel}} = W_{wheel} }[/math]
The rotational kinetic energy of the wheel is given by:
[math]\displaystyle{ K_{rotational} = \frac{1}{2} I_{wheel} \omega_{wheel} }[/math]
Thus, the change in rotational kinetic energy of the wheel will be:
[math]\displaystyle{ \Delta K_{r} = \frac{1}{2} I_{wheel} (\omega^2_{f} - \omega^2_0) = \frac{1}{2} \times 0.175 \times ((43.969)^2 - (25.133)^2) = 113.89 \ J }[/math]
Since we are assuming there is no friction in this process and the center of mass of the wheel does not move, all the work done is due to you pulling the string:
[math]\displaystyle{ W_{you} = \Delta K_{r} = 113.89 \ J }[/math]


Difficult

Image: https://drive.google.com/file/d/185xWvF0iMpX-dUNc91ZOhCxQIq7-hHM3/preview


A common flywheel design is a flattened disk (cylinder) rotating about an axis perpendicular to its center, as shown in the figure. Let’s assume our cylinder is about a meter across ( R = 0.5 m ) and has a mass of 240 kg (i.e. has a weight of about 530 pounds). The moment of inertia for such a shape is [math]\displaystyle{ I = (1/2)MR^2 }[/math]. What velocity do I need the disk to rotate in order to power a house? A typical home uses energy at a rate of roughly 1000 W or 1000 J/s.


[math]\displaystyle{ I = (0.5)*(240)*(0.5)^2 = 30 Kg*m^2 }[/math]

Energy consumption in a day:

[math]\displaystyle{ E{k} = 1000 * 24* 3600 = 8.64 * 10^7 J }[/math]

[math]\displaystyle{ E = (1 / 2)Iw^2 }[/math]

Energy = angular times inertia:

[math]\displaystyle{ w = √(2E/I) }[/math] [math]\displaystyle{ w = √(2*8.64*10^7/30) = 2400 rad/sec }[/math] [math]\displaystyle{ v = r*w = 0.5 * 2400 = 1200 m/sec }[/math]

Connectedness

1. How is this topic connected to something that you are interested in?

  • This topic connected to me because I used to dance when I was younger. This section focused on kinetic energy and the different parts of kinetic energy. You could break up different parts of dance and compare it to kinetic energy.
  • This topic resonated with my tennis experience. If you play tennis there are certain moves that generate specific rotations patterns on the ball and can either increase or decrease the length of its trajectory. Top spin, for example, involves spinning the ball forward and this leads to a positive change in K{rot} and, if we assume no change in K{trans}, an increase in K{total} that extends the ball's trajectory.

2. How is it connected to your major?

  • In Chemical Engineering, we will focus on the kinetic energy on the microscopic level and determining the energy of the particles by looking at the translational, rotational, and vibrational energies of the atom, and how they allow chemical reactions to precess.

3. Is there an interesting industrial application?

  • There are many machines that use kinetic energy for power, and we will probably see in a few years from now the use of rotational, translational, and vibrational energy to power anything from phones to computers.

History

Kinetic energy was first set apart from potential energy by Aristotle. Later, in the 1600's, Leibniz and Bernoulli developed the idea that [math]\displaystyle{ E \propto mv^2 }[/math], and they called it the 'living force.' However, it wasn't until 1829 that Gaspard-Gustave Coriolis showed the first signs of understanding kinetic energy the way that we do today by focusing on the transfer on energy in rotating water wheels. Finally, in 1849, Lord Kelvin is said to have coined the term 'kinetic energy.'

See also

Further Reading

External Links

References

All problem examples, youtube videos, and images are from the websites referenced below:

Retrieved from "http://www.physicsbook.gatech.edu/index.php?title=Translational,_Rotational_and_Vibrational_Energy&oldid=39523"