Pauli exclusion principle: Difference between revisions
Created page with "Claimed by Michael Segal Short Description of Topic ==The Main Idea== State, in your own words, the main idea for this topic ===A Mathematical Model=== What are the math..." |
No edit summary |
||
| (74 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
Claimed by | Claimed by Shamita, April 2022 | ||
The Pauli Exclusion Principle is a quantum mechanical principle that asserts that no two fermions (e.g., electrons in an atom) can occupy the same quantum states simultaneously. Constructed by physicist Wolfgang Pauli in 1925, it is integral to many areas of physics, including astrophysics with degeneracy patterns and energy levels in solid state mechanics. | |||
==The Main Idea== | ==The Main Idea== | ||
For each electron in a molecule, there are four distinct values that describe the state of the electron. | |||
[https://en.wikipedia.org/wiki/Principal_quantum_number Principal Quantum Number] ('''n''') | |||
[https://en.wikipedia.org/wiki/Azimuthal_quantum_number Azimuthal Quantum Number] ('''ℓ''') | |||
[https://en.wikipedia.org/wiki/Magnetic_quantum_number Magnetic Quantum Number] ('''m''') | |||
[https://en.wikipedia.org/wiki/Spin_quantum_number Spin Quantum Number] ('''s''') | |||
One of the main points of the Pauli Exclusion Principle is that no two electrons share the same four values. When electrons fill degenerate energy levels, they must satisfy the Pauli Exclusion Principle and [http://chemwiki.ucdavis.edu/Core/Inorganic_Chemistry/Electronic_Structure_of_Atoms_and_Molecules/Electronic_Configurations/Hund's_Rules Hund's Rule] by not sharing the same orbital and by having parallel spins. This also ends up taking the least amount of energy to fulfill because the electrons interact with one another the least possible amount. | |||
[[File:Si Hund.png|200px|thumb|left|Electrons filling out the orbitals separately, with the same parallel spin.]] | |||
Electrons "space out" while filling the orbitals because electrons act like tiny magnets and repel each other. This means the lower energy level would be to have the electrons spaced further apart. The spins of the electrons are all parallel because the electrons will interact less often if they are all traveling in the same direction, thus lowering the repulsive forces and energy. These two values of electron's direction and position are denoted by '''s''' (spin quantum number) and '''m''' (magnetic quantum number) respectively. | |||
===Properties=== | |||
The Pauli exclusion principle asserts that all particles are either fermions or bosons. Fermions have an odd multiple of half spins. Bosons have an even multiple of half spins, thus result in an integer amount of spin. For example, helium-3 is a fermion with the spin of 1/2 and helium-4 is a boson with the spin of 0. Bosons are not constrained by the Pauli Exclusion Principle like fermions. | |||
The spins have an intrinsic effect on the angular momentum values of a particle. Particles with a half-integer spin (fermions) have antisymmetric states, while particles with a integer spin (bosons) have a symmetric, wavelike functions. | |||
[[File:SymmetricFunction.PNG]] | |||
(Left: Fermion; Right: Boson) | |||
===Fermions=== | |||
As stated above, fermions are constrained by the Pauli Exclusion Principle. This has to do with the fact that the wave function for a fermion with identical half spins ends up being antisymmetric. When fermion particles are swapped with each other, the wave function changes sign. | |||
This can be demonstrated through a general probability equation. The function derived using Pauli Exclusion Principle for fermions is derived as such: | |||
'''Ѱf= Ѱ1(a) * Ѱ2(b) - Ѱ1(b) * Ѱ2(a)''' | |||
Where 'a' and 'b' are the states of electron 1 and electron 2 respectively. The psi greek character represents the 'probability amplitude' that the electron is in its certain state. The equation is equal to the final probability that both states are occupied by electron 1 and 2. This equation proves that it is impossible for both electrons to occupy the same state. If this were the case, then Ѱf would equal 0, meaning the probability is 0. When swapping the two states of the electrons, we end up with a negative version of the same equation. If the states were the same, then the only time the positive wave function and the negative wave function could equal each other is when they are both equal to zero. Proving a second time that two electrons cannot have the same state simultaneously. | |||
===Bosons=== | |||
Unlike fermions, bosons have symmetric wave functions. This means that the wave function of two integer spin particles is identical to the wave function of the two particles with swapped states. The wave function does not change sign or anything. Pauli Exclusion Principle does not pertain to bosons for this reason. | |||
===A Mathematical Model=== | ===A Mathematical Model=== | ||
The typical method for expressing the Pauli Exclusion Principle is through the use of quantum states, primarily by probability amplitude. Expressing | |||
<math> \psi=\psi_{1}(a)\psi_{2}(b) </math>, where <math> \psi </math> designates the overall state. The principle works on the fact that there are four quantum numbers, and we will consider electrons. | |||
<math> n </math> designates the "principle quantum number" and denotes the innermost electron orbital level. As such, it designates the lowest energy level and may occupy values from 1, 2, 3,... but never 0, as this would correspond to no energy and thus no particle. | |||
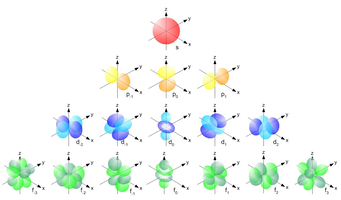
<math> l </math> denotes the "angular momentum orbital number" indicates the orientation and shape of the orbitals, as demonstrated below. It may possess values from <math> n - 1 </math>, hence it may be 0. | |||
[[File:Orbital Shapes.png]] | |||
<math> m_{l} </math> is the "magnetic quantum number" and exists from <math> -l </math> to <math> +l </math>. It determines subshell orinetation. | |||
Finally, <math> m_{s} </math>, the "spin quantum number". For the purpose of an electron, this may only be values of -1/2 or +1/2, where it is understood these correspond to "spin-down" and "spin-up" values of -ℏ/2 or ℏ/2, respectively. | |||
===A Computational Model: Stellar Degeneracy=== | |||
A primary aspect of the Pauli Exclusion Principle is its prevalence in the concept of "degeneracy", particularly evident in stellar evolution and supernovae incitement. As a star evolves, heavier material precipitates towards the core, causing the star to collapse into itself. Simultaneously, the pressure of the electrons in the star exert an outward pressure due to the Pauli Exclusion Principle. When the star attempts to contract, this motion creates a decreasing volume for the electrons to occupy. The electrons first attempt to fill lower energy levels; however, as the volume constricts the lower energy levels are occupied and the electrons are forced into higher energy states. This higher energy contributes to their speed, which creates "electron degeneracy pressure", allowing the star to support itself against the weight of gravity. | |||
The Pauli Exclusion Principle is vital to this phenomenon, as when volume decrease one is fundamentally attempting to force the stellar electrons into the same quantum state. The resistance manifests as an outward pressure related to the Heisenberg Uncertainty Principle, for a decrease in volume couples with an increase in knowledge about a particle's position, thus additionally contributing to an increased uncertainty in momentum and thus higher energy states. | |||
[[File:Stellar N. Radius vs. Pressure.PNG|Plot of Normalised Radius vs. Pressure for a 2 Solar Mass star]] | |||
As depicted in the figure above, as radius decreases (i.e., the star contracts), the measurable outward pressure skyrockets, indicating the presence of the Pauli Exclusion Principle in the form of degeneracy pressure. Additionally, if considering solely a single, non-contracting star, distance to the core denotes in the form of radius and demonstrates that the Pauli Exclusion Principle affirms Newton's Third Law of Equal and Opposite Reaction. As gravitational forces increase towards the centre of the body, the degenerate pressure caused by resisting electrons asserts itself more and causes an exponential growth in pressure. This feature is present in neutron stars as well, contributing to "neutron degeneracy pressure". | |||
[[File:Normalised_Radius_vs._Luminosity_Per_Cent.PNG]] | |||
In addition, should the Pauli Exclusion Principle hold true and enforce higher energy states, one would expect an increase in luminosity for the stars as radius decreases. The figure above depicts just that for the case of a 2 Solar Mass star. | |||
Regarding the Pauli Exclusion Principle overall, the PhET simulation "Build An Atom" provides a resource towards understanding the order of orbital-filling and thus a fundamental aspect of the Pauli Exclusion Principle. | |||
http://phet.colorado.edu/sims/html/build-an-atom/latest/build-an-atom_en.html | |||
==Examples== | ==Examples== | ||
===Simple=== | |||
Considering the Pauli Exclusion Principle's correspondence to the orbital filling order for electrons, it is suffice to say that due to electrons not being able to possess the same quantum state, each atomic orbital block (e.g., 1s, 1p, 1/3 of 2p etc.) may only possess a maximum of two electrons, one being spin-up and the other spin-down. The fill in accordance to the diagram below. | |||
[[File:Orbital_Filling_Diagram.PNG]] | |||
It is important to note that the s orbital possesses two possible electron slots, and p possesses 6. D possesses 10 and f 14. As such, for a simple example, if one wanted to compute the electron configuration for neutral Phosphorus, one would only need to follow the diagonals on the orbital filling diagram until the number of electrons in Phosphorus is reached (15). From this, one may see that the orbital level follows as below: | |||
[[File:]] | |||
==History== | ==History== | ||
The Pauli exclusion principle is named after Austrian physicist Wolfgang Pauli. Pauli proposed the assertion in 1925 and received a Nobel Prize in 1945 for his discovery. He is considered a founding father of quantum mechanics and discovered many of his theories and principles without a formal existing definition of what we today call "spin". | |||
Pauli's discovery and implementation of a fourth quantum number laid the groundwork and inspiration for quantum mechanics in the next years following its announcement. Much of Heisenberg's and Schrodinger's discoveries on wave mechanics were built off of the Pauli exclusion principle. | |||
==Importance/Connectedness== | |||
The significance of the Pauli exclusion Principle is that it introduced a fourth quantum number. While spin is not a physical characteristic, it is crucial when determining shapes and wavelike behaviors of atomic particles. The principle dictates that bosons have probability waves which "flip" as they move and interfere with each other. The interference of these probability waves leads to collective behavior that can result in lasers, super fluids and superconductors. Conversely, fermions do not flip their probability waves and do not interact with each other. Fermions include electrons, protons and neutrons. | |||
The Pauli Exclusion Principle, as denoted earlier, is additionally integral towards understanding stellar death and the process of evolution, for without the Pauli Exclusion Principle stars would have no form of support and would succumb to the crush of gravity. The Pauli Exclusion Principle works in tandem with other known laws of the universe, such as Heisenberg's Uncertainty Principle, to provide a counter force under weight. In short, it is vital to fundamental processes of the universe and provides information about astrophysics and solid state work. | |||
==See Also== | |||
There are plenty of great YouTube videos that can explain the Pauli Exclusion Principle. The Pauli Exclusion Principle is closely related to Hund's Rule and most videos introduce both topics in conjunction. Click on the following link to learn more about Pauli Exclusion Principle and Hund's Rule: https://www.youtube.com/watch?v=9WA8BeE3jRw | |||
Another closely related topic is Heisenberg's Uncertainty Principle which basically states that the momentum and position of a particle cannot be found at the same time. Hyper Physics is a great forum for physics topics and has a short page dedicated to Heisenberg's Principle: http://hyperphysics.phy-astr.gsu.edu/hbase/uncer.html | |||
If you are feeling ambitious and would like to know the quantum physics behind the antisymmetric and symmetric wave functions of the fermions and bosons, there is a great Wikipedia page which outlines the equations in more detail: https://en.wikipedia.org/wiki/Spin%E2%80%93statistics_theorem | |||
== | ==Sources== | ||
Hyper Physics: http://hyperphysics.phy-astr.gsu.edu/hbase/pauli.html | |||
Wikipedia: https://en.wikipedia.org/wiki/Quantum_number | |||
Physics of the Universe: http://www.physicsoftheuniverse.com/topics_quantum_spin.html | |||
APS: http://www.aps.org/publications/apsnews/200701/history.cfm | |||
Chem Wiki: http://chemwiki.ucdavis.edu/Core/Inorganic_Chemistry/Electronic_Structure_of_Atoms_and_Molecules/Electronic_Configurations/Hund's_Rules | |||
Computational Models created by Shamita Hanumasagar | |||
PhET Colorado, Creative Commons Attribution 4.0. | |||
Latest revision as of 12:46, 25 April 2022
Claimed by Shamita, April 2022
The Pauli Exclusion Principle is a quantum mechanical principle that asserts that no two fermions (e.g., electrons in an atom) can occupy the same quantum states simultaneously. Constructed by physicist Wolfgang Pauli in 1925, it is integral to many areas of physics, including astrophysics with degeneracy patterns and energy levels in solid state mechanics.
The Main Idea
For each electron in a molecule, there are four distinct values that describe the state of the electron.
One of the main points of the Pauli Exclusion Principle is that no two electrons share the same four values. When electrons fill degenerate energy levels, they must satisfy the Pauli Exclusion Principle and Hund's Rule by not sharing the same orbital and by having parallel spins. This also ends up taking the least amount of energy to fulfill because the electrons interact with one another the least possible amount.

Electrons "space out" while filling the orbitals because electrons act like tiny magnets and repel each other. This means the lower energy level would be to have the electrons spaced further apart. The spins of the electrons are all parallel because the electrons will interact less often if they are all traveling in the same direction, thus lowering the repulsive forces and energy. These two values of electron's direction and position are denoted by s (spin quantum number) and m (magnetic quantum number) respectively.
Properties
The Pauli exclusion principle asserts that all particles are either fermions or bosons. Fermions have an odd multiple of half spins. Bosons have an even multiple of half spins, thus result in an integer amount of spin. For example, helium-3 is a fermion with the spin of 1/2 and helium-4 is a boson with the spin of 0. Bosons are not constrained by the Pauli Exclusion Principle like fermions.
The spins have an intrinsic effect on the angular momentum values of a particle. Particles with a half-integer spin (fermions) have antisymmetric states, while particles with a integer spin (bosons) have a symmetric, wavelike functions.
(Left: Fermion; Right: Boson)
Fermions
As stated above, fermions are constrained by the Pauli Exclusion Principle. This has to do with the fact that the wave function for a fermion with identical half spins ends up being antisymmetric. When fermion particles are swapped with each other, the wave function changes sign.
This can be demonstrated through a general probability equation. The function derived using Pauli Exclusion Principle for fermions is derived as such:
Ѱf= Ѱ1(a) * Ѱ2(b) - Ѱ1(b) * Ѱ2(a)
Where 'a' and 'b' are the states of electron 1 and electron 2 respectively. The psi greek character represents the 'probability amplitude' that the electron is in its certain state. The equation is equal to the final probability that both states are occupied by electron 1 and 2. This equation proves that it is impossible for both electrons to occupy the same state. If this were the case, then Ѱf would equal 0, meaning the probability is 0. When swapping the two states of the electrons, we end up with a negative version of the same equation. If the states were the same, then the only time the positive wave function and the negative wave function could equal each other is when they are both equal to zero. Proving a second time that two electrons cannot have the same state simultaneously.
Bosons
Unlike fermions, bosons have symmetric wave functions. This means that the wave function of two integer spin particles is identical to the wave function of the two particles with swapped states. The wave function does not change sign or anything. Pauli Exclusion Principle does not pertain to bosons for this reason.
A Mathematical Model
The typical method for expressing the Pauli Exclusion Principle is through the use of quantum states, primarily by probability amplitude. Expressing [math]\displaystyle{ \psi=\psi_{1}(a)\psi_{2}(b) }[/math], where [math]\displaystyle{ \psi }[/math] designates the overall state. The principle works on the fact that there are four quantum numbers, and we will consider electrons.
[math]\displaystyle{ n }[/math] designates the "principle quantum number" and denotes the innermost electron orbital level. As such, it designates the lowest energy level and may occupy values from 1, 2, 3,... but never 0, as this would correspond to no energy and thus no particle.
[math]\displaystyle{ l }[/math] denotes the "angular momentum orbital number" indicates the orientation and shape of the orbitals, as demonstrated below. It may possess values from [math]\displaystyle{ n - 1 }[/math], hence it may be 0.
[math]\displaystyle{ m_{l} }[/math] is the "magnetic quantum number" and exists from [math]\displaystyle{ -l }[/math] to [math]\displaystyle{ +l }[/math]. It determines subshell orinetation.
Finally, [math]\displaystyle{ m_{s} }[/math], the "spin quantum number". For the purpose of an electron, this may only be values of -1/2 or +1/2, where it is understood these correspond to "spin-down" and "spin-up" values of -ℏ/2 or ℏ/2, respectively.
A Computational Model: Stellar Degeneracy
A primary aspect of the Pauli Exclusion Principle is its prevalence in the concept of "degeneracy", particularly evident in stellar evolution and supernovae incitement. As a star evolves, heavier material precipitates towards the core, causing the star to collapse into itself. Simultaneously, the pressure of the electrons in the star exert an outward pressure due to the Pauli Exclusion Principle. When the star attempts to contract, this motion creates a decreasing volume for the electrons to occupy. The electrons first attempt to fill lower energy levels; however, as the volume constricts the lower energy levels are occupied and the electrons are forced into higher energy states. This higher energy contributes to their speed, which creates "electron degeneracy pressure", allowing the star to support itself against the weight of gravity.
The Pauli Exclusion Principle is vital to this phenomenon, as when volume decrease one is fundamentally attempting to force the stellar electrons into the same quantum state. The resistance manifests as an outward pressure related to the Heisenberg Uncertainty Principle, for a decrease in volume couples with an increase in knowledge about a particle's position, thus additionally contributing to an increased uncertainty in momentum and thus higher energy states.
As depicted in the figure above, as radius decreases (i.e., the star contracts), the measurable outward pressure skyrockets, indicating the presence of the Pauli Exclusion Principle in the form of degeneracy pressure. Additionally, if considering solely a single, non-contracting star, distance to the core denotes in the form of radius and demonstrates that the Pauli Exclusion Principle affirms Newton's Third Law of Equal and Opposite Reaction. As gravitational forces increase towards the centre of the body, the degenerate pressure caused by resisting electrons asserts itself more and causes an exponential growth in pressure. This feature is present in neutron stars as well, contributing to "neutron degeneracy pressure".
In addition, should the Pauli Exclusion Principle hold true and enforce higher energy states, one would expect an increase in luminosity for the stars as radius decreases. The figure above depicts just that for the case of a 2 Solar Mass star.
Regarding the Pauli Exclusion Principle overall, the PhET simulation "Build An Atom" provides a resource towards understanding the order of orbital-filling and thus a fundamental aspect of the Pauli Exclusion Principle.
http://phet.colorado.edu/sims/html/build-an-atom/latest/build-an-atom_en.html
Examples
Simple
Considering the Pauli Exclusion Principle's correspondence to the orbital filling order for electrons, it is suffice to say that due to electrons not being able to possess the same quantum state, each atomic orbital block (e.g., 1s, 1p, 1/3 of 2p etc.) may only possess a maximum of two electrons, one being spin-up and the other spin-down. The fill in accordance to the diagram below.
It is important to note that the s orbital possesses two possible electron slots, and p possesses 6. D possesses 10 and f 14. As such, for a simple example, if one wanted to compute the electron configuration for neutral Phosphorus, one would only need to follow the diagonals on the orbital filling diagram until the number of electrons in Phosphorus is reached (15). From this, one may see that the orbital level follows as below:
[[File:]]
History
The Pauli exclusion principle is named after Austrian physicist Wolfgang Pauli. Pauli proposed the assertion in 1925 and received a Nobel Prize in 1945 for his discovery. He is considered a founding father of quantum mechanics and discovered many of his theories and principles without a formal existing definition of what we today call "spin".
Pauli's discovery and implementation of a fourth quantum number laid the groundwork and inspiration for quantum mechanics in the next years following its announcement. Much of Heisenberg's and Schrodinger's discoveries on wave mechanics were built off of the Pauli exclusion principle.
Importance/Connectedness
The significance of the Pauli exclusion Principle is that it introduced a fourth quantum number. While spin is not a physical characteristic, it is crucial when determining shapes and wavelike behaviors of atomic particles. The principle dictates that bosons have probability waves which "flip" as they move and interfere with each other. The interference of these probability waves leads to collective behavior that can result in lasers, super fluids and superconductors. Conversely, fermions do not flip their probability waves and do not interact with each other. Fermions include electrons, protons and neutrons.
The Pauli Exclusion Principle, as denoted earlier, is additionally integral towards understanding stellar death and the process of evolution, for without the Pauli Exclusion Principle stars would have no form of support and would succumb to the crush of gravity. The Pauli Exclusion Principle works in tandem with other known laws of the universe, such as Heisenberg's Uncertainty Principle, to provide a counter force under weight. In short, it is vital to fundamental processes of the universe and provides information about astrophysics and solid state work.
See Also
There are plenty of great YouTube videos that can explain the Pauli Exclusion Principle. The Pauli Exclusion Principle is closely related to Hund's Rule and most videos introduce both topics in conjunction. Click on the following link to learn more about Pauli Exclusion Principle and Hund's Rule: https://www.youtube.com/watch?v=9WA8BeE3jRw
Another closely related topic is Heisenberg's Uncertainty Principle which basically states that the momentum and position of a particle cannot be found at the same time. Hyper Physics is a great forum for physics topics and has a short page dedicated to Heisenberg's Principle: http://hyperphysics.phy-astr.gsu.edu/hbase/uncer.html
If you are feeling ambitious and would like to know the quantum physics behind the antisymmetric and symmetric wave functions of the fermions and bosons, there is a great Wikipedia page which outlines the equations in more detail: https://en.wikipedia.org/wiki/Spin%E2%80%93statistics_theorem
Sources
Hyper Physics: http://hyperphysics.phy-astr.gsu.edu/hbase/pauli.html
Wikipedia: https://en.wikipedia.org/wiki/Quantum_number
Physics of the Universe: http://www.physicsoftheuniverse.com/topics_quantum_spin.html
APS: http://www.aps.org/publications/apsnews/200701/history.cfm
Computational Models created by Shamita Hanumasagar
PhET Colorado, Creative Commons Attribution 4.0.