Einstein's Theory of Special Relativity: Difference between revisions

From Physics Book
Jump to navigation Jump to search
m (Changed normal text math into LaTex)
 
(44 intermediate revisions by one other user not shown)
Line 3: Line 3:
==Special Relativity==
==Special Relativity==


Einstein's Theory of Special relativity is based on an invariant speed of light.  
Einstein's Theory of Special relativity is a theory used to describe space and time for observers at different speeds based on an invariant speed of light. His theory consists of two postulates from which consequences arose that changed our understanding of spacetime.


[[File:2000px-World_line.svg.png|200px|thumb|Special relativity]]
[[File:200px-World_line.svg.png|200px|thumb|Spacetime Diagram]]


[[File:733a1857c551ba67e3f9edf771a9efd6.png|200px|thumb|Energy and mass equivalence]]
===Einstein's Postulates===
 
===Relativistic vs. Nonrelativistic===
If the ratio between the velocity of a particle, v, and the speed of light, c, is close to one, typically defined as v/c >= .1, then the particle is moving at relativistic speeds, and Special Relativity must be used to describe the motion of the object. If not, it is moving at non-relativistic speeds, then Newtonian mechanics is sufficient to describe the particle.
 
==Einstein's Postulates==
Einstein's theory of special relativity results from two statements -- the two basic postulates of special relativity:
Einstein's theory of special relativity results from two statements -- the two basic postulates of special relativity:


[[File:albert_einstein_quote.jpg|thumb|Einstein Quote]]
#Speed of Light Postulate: The speed of light, c, is the same for all observers, no matter what their relative speeds.    c = 299,792,458 m/s
#The Relativity Postulate: The laws of physics are the same in any inertial (that is, non-accelerated) frame of reference. This means that the laws of physics observed by a hypothetical observer traveling with a relativistic particle must be the same as those observed by an observer who is stationary in the laboratory.


#The speed of light is the same for all observers, no matter what their relative speeds.
Given these two statements, Einstein showed how definitions of momentum and energy must be refined and how quantities such as length and time must change from one observer to another in order to get consistent results for physical quantities such as particle half-life.
#The laws of physics are the same in any inertial (that is, non-accelerated) frame of reference. This means that the laws of physics observed by a hypothetical observer traveling with a relativistic particle must be the same as those observed by an observer who is stationary in the laboratory.


[[File:18lqemuokd26vjpg.jpg|thumb|The speed of light]]
[[File:733a1857c551ba67e3f9edf771a9efd6.png]]


Given these two statements, Einstein showed how definitions of momentum and energy must be refined and how quantities such as length and time must change from one observer to another in order to get consistent results for physical quantities such as particle half-life.
===Relativistic vs. Nonrelativistic===
To determine whether Special Relativity is necessary to describe the motion of a particle, we must look at the ratio of its speed to that of the speed of light.


===The speed of light is the same for all observers, no matter what their relative speeds===
If the ratio between the velocity of a particle, <math>v</math>, and the speed of light, <math>c</math>, is close to one, typically defined as <math>\frac{v}{c} \geq .1 </math>, then the particle is moving at relativistic speeds, and Special Relativity must be used to describe the motion of the object. If not, it is moving at non-relativistic speeds, then Newtonian mechanics is sufficient to describe the particle.
*'''"The speed of light will be seen to be the same relative to any observer, independent of the motion of the observer"'''is the crucial idea that led Einstein to formulate his theory. It means we can define a quantity c, the speed of light, which is a fundamental constant of nature.
*Note that this is quite different from the motion of ordinary, massive objects. If I am driving down the freeway at 50 miles per hour relative to the road, a car traveling in the same direction at 55 mph has a speed of only 5 mph relative to me, while a car coming in the opposite direction at 55 mph approaches me at a rate of 105 mph. Their speed relative to me depends on my motion as well as on theirs.
===The laws of physics are the same in any inertial (that is, non-accelerated) frame of reference===
*This is the idea that we can formulate rules of nature which do not depend on our particular observing situation. This does not mean that things behave in the same way on the earth and in space, e.g. an observer at the surface of the earth is affected by the earth's gravity, but it does mean that the effect of a force on an object is the same independent of what causes the force and also of where the object is or what its speed is.
*Einstein developed a theory of motion that could consistently contain both the same speed of light for any observer and the familiar addition of velocities described above for slow-moving objects. This is called '''the special theory of relativity''', since it deals with the relative motions of objects.


[[File:183224.image0.jpg]]
[[File:Relativistic_vs_nonrelativistic.png]]


==History==
==History==
Line 38: Line 29:


On September 26, 1905 (received June 30), Einstein published his annus mirabilis paper on what is now called special relativity. Einstein's paper includes a fundamental new definition of space and time (all time and space coordinates in all reference frames are on an equal footing, so there is no physical basis for distinguishing "true" from "apparent" time) and makes the aether an unnecessary concept, at least in regard to inertial motion. Einstein identified two fundamental principles, the principle of relativity and the principle of the constancy of light (light principle), which ostensibly served as the axiomatic basis of his theory. [http://www.space.com/17661-theory-general-relativity.html]
On September 26, 1905 (received June 30), Einstein published his annus mirabilis paper on what is now called special relativity. Einstein's paper includes a fundamental new definition of space and time (all time and space coordinates in all reference frames are on an equal footing, so there is no physical basis for distinguishing "true" from "apparent" time) and makes the aether an unnecessary concept, at least in regard to inertial motion. Einstein identified two fundamental principles, the principle of relativity and the principle of the constancy of light (light principle), which ostensibly served as the axiomatic basis of his theory. [http://www.space.com/17661-theory-general-relativity.html]


With the following consequences for the speed of light and the theories known at that time:
With the following consequences for the speed of light and the theories known at that time:
Line 52: Line 42:


Einstein himself did not know of the Michelson-Morley Experiment, as his reasoning was purely to reconcile Maxwell's equations from inconsistency with Newtonian Mechanics. However, Lorentz transforms fit in perfectly with special relativity, and although their physical basis was unknown when Lorentz created them, they are now understood physically.
Einstein himself did not know of the Michelson-Morley Experiment, as his reasoning was purely to reconcile Maxwell's equations from inconsistency with Newtonian Mechanics. However, Lorentz transforms fit in perfectly with special relativity, and although their physical basis was unknown when Lorentz created them, they are now understood physically.
[[File:The-setup-of-the-Michelson---Morley-Experiment.png]]


==Mathematics of Special Relativity==
==Mathematics of Special Relativity==
===Gamma(γ)===
The measurable effects of relativity are based on gamma. Gamma depends only on the speed of a particle and is always larger than
By definition: [[File:Eq-gamma.gif]]  c is the speed of light and v is the speed of the object in question
For example, when an electron has traveled ten feet along the accelerator it has a speed of 0.99 c, and the value of gamma at that speed is 7.09. When the electron reaches the end of the linac, its speed is 0.99999999995 c where gamma equals 100,000.


[[File:Lorentz_factor.svg.png|thumb|Lorentz factor γ as a function of velocity. Its initial value is 1 (when v = 0); and as velocity approaches the speed of light (v → c) γ increases without bound (γ → ∞).]]
The thought experiment[https://youtu.be/wteiuxyqtoM] Einstein used was that of 2 observers, observer A in a train, observer B on a platform. As the center of the train passes Observer B, he views 2 bolts of lightning strike both the front and back of the train simultaneously. However, Observer A is sitting midway of the train and views a bolt of lighting strike the front and then the back of the train. Who is right?


[[File:TimeDilation.gif]]
According to Einstein, both are right.


===Relativistic Effects===
[[File:Einstein_train_relativity_of_simultaneity2.png]]
====Length Contraction and Time Dilation====
One of the strangest parts of special relativity is the conclusion that two observers who are moving relative to one another, will get different measurements of the length of a particular object or the time that passes between two events.


We will now derive the math to be able to have a dictionary between these 2 equivalent reference frames. We will be able to derive these by using the Speed of Light postulate.


[[File:Figure_29_03_03a.jpg]]
===Time Dilation===
[[File:TD 3564.jpg]]


From Time Dilation, we now have found a constant gamma:
====Gamma(γ)====
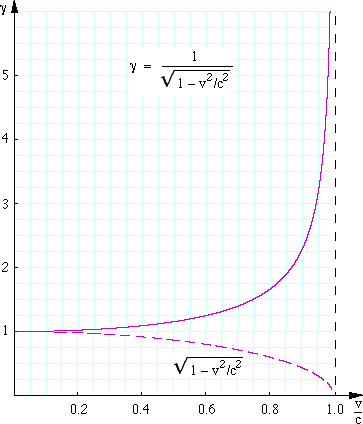
The measurable effects of relativity are based on gamma. Gamma depends only on the speed of a particle and is always larger than 1.


Consider two observers, each in a space-ship laboratory containing clocks and meter sticks. The space ships are moving relative to each other at a speed close to the speed of light. Using Einstein's theory:
By definition: [[File:Eq-gamma.gif]]  c is the speed of light and v is the speed of the object in question.
 
*Each observer will see the meter stick of the other as shorter than their own, by the same factor gamma (gamma- defined above). This is called length contraction .
*Each observer will see the clocks in the other laboratory as ticking more slowly than the clocks in his/her own, by a factor gamma. This is called time dilation .
 
In particle accelerators, particles are moving very close to the speed of light where the length and time effects are large. This has allowed us to clearly verify that length contraction and time dilation do occur.


[[File:gamma.GIF]]
[[File:gamma.GIF]]


====Time Dilation for Particles====
===Length Contraction===
Particle processes have an intrinsic clock that determines the half-life of a decay process. However, the rate at which the clock ticks in a moving frame, as observed by a static observer, is slower than the rate of a static clock. Therefore, the half-life of a moving particles appears, to the static observer, to be increased by the factor gamma. [http://pages.towson.edu/zverev/conceptual/14.htm]


For example, let's look at a particle known as a tau. In the  frame of reference where the tau particle is at rest, its lifetime is known to be approximately 3.05 x 10 -13 s. To calculate how far it travels before decaying, we could try to use the familiar equation distance equals speed times time. It travels so close to the speed of light that we can use c = 3x10^8 m/sec for the speed of the particle. If you do the calculation you find the distance traveled should be 9.15 x 10 -5 meters.
[[File:LC 3565.jpg]]


:::'''d = v t'''
Illustration of length contraction in direction of motion:


:::'''d = (3 x 10^8 m/sec)( 3.05 x 10^-13 s) = 9.15 x 10^-5 m'''
[[File:tallball.jpg]]
 
[[File:Relativity-1-10-728.jpg|thumb|The apparent slowing down of time for an object moving at relativistic speeds]]
 
 
Observations particles with a variety of velocities have shown that time dilation is a real effect. In fact the only reason cosmic ray muons ever reach the surface of the earth before decaying is the time dilation effect.
 
====Length Contraction====
Instead of analyzing the motion of the tau from our frame of reference, we could ask what the tau would see in its reference frame. Its half-life in its reference frame is 3.05 x 10^-13 s. This does not change. The tau goes nowhere in this frame.
 
How far would an observer, sitting in the tau rest frame, see an observer in our laboratory frame move while the tau lives [http://pages.towson.edu/zverev/conceptual/14.htm]


We just calculated that the tau would travel 1.8 mm in our frame of reference. Surely we would expect the observer in the tau frame to see us move the same distance relative to the tau particle. Not so says the tau-frame observer -- you only moved 1.8 mm/gamma = 0.09 mm relative to me. This is length contraction.
====Simulation====
Trinket Simulation:
[https://trinket.io/python/ca38e9a838]


How long did the tau particle live according to the observer in the tau frame? We can rearrange d = v x t to read t = d/v . Here we use the same speed, Because the speed of the observer in the lab relative to the tau is just equal to (but in the opposite direction) of the speed of the tau relative to the observer in the lab, so we can use the same speed. So time = 0.09 x 10^-3 m/(3 x 10^8) m/sec  = 3.0 x 10^-13 sec. This is the half-life of the tau as seen in its rest frame, just as it should be!
Graphical Glowscript Simulation: (because Trinket SUCKS!)
[https://www.glowscript.org/#/user/mrheadhunter34/folder/MyPrograms/program/LengthContraction]


[[File:tallball.jpg]]
===Relativistic Energy===
[[File:RE 3566.jpg]]


==Examples==
==Examples==

Latest revision as of 20:44, 28 September 2022

claimed by Arihant Gadgade Spring 2022

Special Relativity

Einstein's Theory of Special relativity is a theory used to describe space and time for observers at different speeds based on an invariant speed of light. His theory consists of two postulates from which consequences arose that changed our understanding of spacetime.

Spacetime Diagram

Einstein's Postulates

Einstein's theory of special relativity results from two statements -- the two basic postulates of special relativity:

  1. Speed of Light Postulate: The speed of light, c, is the same for all observers, no matter what their relative speeds. c = 299,792,458 m/s
  2. The Relativity Postulate: The laws of physics are the same in any inertial (that is, non-accelerated) frame of reference. This means that the laws of physics observed by a hypothetical observer traveling with a relativistic particle must be the same as those observed by an observer who is stationary in the laboratory.

Given these two statements, Einstein showed how definitions of momentum and energy must be refined and how quantities such as length and time must change from one observer to another in order to get consistent results for physical quantities such as particle half-life.

Relativistic vs. Nonrelativistic

To determine whether Special Relativity is necessary to describe the motion of a particle, we must look at the ratio of its speed to that of the speed of light.

If the ratio between the velocity of a particle, [math]\displaystyle{ v }[/math], and the speed of light, [math]\displaystyle{ c }[/math], is close to one, typically defined as [math]\displaystyle{ \frac{v}{c} \geq .1 }[/math], then the particle is moving at relativistic speeds, and Special Relativity must be used to describe the motion of the object. If not, it is moving at non-relativistic speeds, then Newtonian mechanics is sufficient to describe the particle.

History

Prior to Special Relativity, Maxwell's Equations were inconsistent with Newtonian mechanics. Albert Einstein then sought out to correct mechanics to be consistent with Maxwell's Equations.

On September 26, 1905 (received June 30), Einstein published his annus mirabilis paper on what is now called special relativity. Einstein's paper includes a fundamental new definition of space and time (all time and space coordinates in all reference frames are on an equal footing, so there is no physical basis for distinguishing "true" from "apparent" time) and makes the aether an unnecessary concept, at least in regard to inertial motion. Einstein identified two fundamental principles, the principle of relativity and the principle of the constancy of light (light principle), which ostensibly served as the axiomatic basis of his theory. [1]

With the following consequences for the speed of light and the theories known at that time:

  • The speed of light is not composed of the speed of light in vacuum and the velocity of a preferred frame of reference, by b. This contradicts the theory of the (nearly) stationary aether.
  • The speed of light is not composed of the speed of light in vacuum and the velocity of the light source, by a and c. This contradicts the emission theory.
  • The speed of light is not composed of the speed of light in vacuum and the velocity of an aether that would be dragged within or in the vicinity of matter, by a, c, and d. This contradicts the hypothesis of the complete aether drag.
  • The speed of light in moving media is not composed of the speed of light when the medium is at rest and the velocity of the medium, but is determined by Fresnel's dragging coefficient, by c.

Michelson-Morley Experiment

The Michelson-Morley Experiment published the initial null result of the aether, essentially providing evidence against the aether. This came as a severe shock to the scientific community, as Maxwell's equations relied on the presence of an aether. One physicist, Hendrik Lorentz, then created a mathematical transformation, called the Lorentz Transform, which allowed the lengths in the direction of motion to contract by a factor, which we now refer to as gamma. This Lorentz Transform forced path lengths to be equal and phase shifts to be zero. However, there was no insight as to why this was true.

Einstein himself did not know of the Michelson-Morley Experiment, as his reasoning was purely to reconcile Maxwell's equations from inconsistency with Newtonian Mechanics. However, Lorentz transforms fit in perfectly with special relativity, and although their physical basis was unknown when Lorentz created them, they are now understood physically.

Mathematics of Special Relativity

The thought experiment[2] Einstein used was that of 2 observers, observer A in a train, observer B on a platform. As the center of the train passes Observer B, he views 2 bolts of lightning strike both the front and back of the train simultaneously. However, Observer A is sitting midway of the train and views a bolt of lighting strike the front and then the back of the train. Who is right?

According to Einstein, both are right.

We will now derive the math to be able to have a dictionary between these 2 equivalent reference frames. We will be able to derive these by using the Speed of Light postulate.

Time Dilation

From Time Dilation, we now have found a constant gamma:

Gamma(γ)

The measurable effects of relativity are based on gamma. Gamma depends only on the speed of a particle and is always larger than 1.

By definition: c is the speed of light and v is the speed of the object in question.

Length Contraction

Illustration of length contraction in direction of motion:

Simulation

Trinket Simulation: [3]

Graphical Glowscript Simulation: (because Trinket SUCKS!) [4]

Relativistic Energy

Examples

Simple

Problem

Solution

Middling

Problem

Solution


Difficult

Problem


Solution


Real World Connections of Special Relativity

Einstein's Theory of Special Relativity is connected to the general relativity. The movie "Interstellar" made me interested about the Einstein's Theorem. It is not directly related to Business major, but there are some interesting industrial applications.

Error creating thumbnail: sh: /usr/bin/convert: No such file or directory Error code: 127
Telescopes around the Earth

Built at a cost of over $10 billion mainly for military navigation, GPS has rapidly transformed itself into a thriving commercial industry. The system is based on an array of 24 satellites orbiting the earth, each carrying a precise atomic clock. Apart from the obvious military uses, GPS is finding applications in airplane navigation, oil exploration, wilderness recreation, bridge construction, sailing, and interstate trucking, to name just a few.

The satellite clocks are moving at 14,000 km/hr in orbits that circle the Earth twice per day, much faster than clocks on the surface of the Earth, and Einstein's theory of special relativity says that rapidly moving clocks tick more slowly, by about seven microseconds (millionths of a second) per day.

Also, the orbiting clocks are 20,000 km above the Earth, and experience gravity that is four times weaker than that on the ground. Einstein's general relativity theory says that gravity curves space and time, resulting in a tendency for the orbiting clocks to tick slightly faster, by about 45 microseconds per day. The net result is that time on a GPS satellite clock advances faster than a clock on the ground by about 38 microseconds per day. [5]

To determine its location, the GPS receiver uses the time at which each signal from a satellite was emitted, as determined by the on-board atomic clock and encoded into the signal, together the with speed of light, to calculate the distance between itself and the satellites it communicated with. The orbit of each satellite is known accurately. Given enough satellites, it is a simple problem in Euclidean geometry to compute the receiver's precise location, both in space and time. To achieve a navigation accuracy of 15 meters, time throughout the GPS system must be known to an accuracy of 50 nanoseconds, which simply corresponds to the time required for light to travel 15 meters.

GPS accounts for relativity by electronically adjusting the rates of the satellite clocks, and by building mathematical corrections into the computer chips which solve for the user's location. Without the proper application of relativity, GPS would fail in its navigational functions within about 2 minutes.

Interesting Facts About Special Relativity

  • Philosopher David Hume's 1738 "A Treatise of Human Nature" was a big influence on Einstein's thinking about space and time. Hume was an empiricist and skeptic, believing that scientific concepts must be based on experience and evidence, not reason alone. He also held that time did not exist separately from the movement of objects. "It is very well possible that without these philosophical studies I would not have arrived at the solution," Einstein wrote.[6]
David Hume's Treatise of Human Nature
  • In 1905, Albert Einstein based a new theory on two principles. First, the laws of physics appear the same to all observers. Second, he calculated that the speed of light-186,000 miles per second (299,338 kilometers per second)- is unchanging. Prior to Einstein, scientists believed that space was filled with luminiferous aether that would cause the speed of light to change depending on the relative motion of the source and the observer.
Error creating thumbnail: sh: /usr/bin/convert: No such file or directory Error code: 127
Time Lapse
  • As a result of these principles, Einstein deduced that there is no fixed frame of reference in the universe. Everything is moving relative to everything else, hence Einstein's theory of relativity. It is known as special relativity because it applies only to special cases: frames of reference in constant, unchanging motion. In 1915, Einstein published the general theory of relativity, which applies to frames that are accelerating with regard to each other.[7]
  • A fast-moving object appears shorter along the direction of motion, relative to a slow-moving one. This effect is very subtle until the object travels close to the speed of light.
  • As a result of 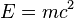, a fast-moving object appears to have increased masses relative to a slow-moving one. This is due to the fact that increasing an object's velocity increases its kinetic energy and, therefore, its mass.[8]

See also

Further reading

External links

References

  1. Towson University
  2. Towson University
  3. Physics Central
  4. Space.com
  5. Space.com
  6. Space.com
  7. Space.com
Retrieved from "http://www.physicsbook.gatech.edu/index.php?title=Einstein%27s_Theory_of_Special_Relativity&oldid=40945"