Energy of a Single Particle: Difference between revisions
Parkercoye (talk | contribs) |
No edit summary |
||
| (28 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
Claimed by Samyukta Iyer - Fall 2022 | |||
Elif Kulaksizoglu Fall 2019 | |||
== | == The Main Idea == | ||
We are going to take a side step from the macroscopic world for a moment, and focus on the energy of very small particles | We are going to take a side step from the macroscopic world for a moment, and focus on the energy of very small (subatomic) particles, such as protons, neutrons, and electrons. | ||
===Point Particles (a closer look)=== | |||
[[File:Carbon atom (Bohr model).png|thumb|Carbon atom (Bohr model)]] | |||
[[File: | |||
'''Types of point particles:''' | '''Types of point particles:''' | ||
*1. Electrons | *1. Electrons (seen as green particles in orbitals of atom) | ||
*2. Protons | *2. Protons (seen as black particles in nucleus of atom) | ||
*3. Neutrons | *3. Neutrons (seen as white particles in nucleus of atom) | ||
| Line 22: | Line 20: | ||
*3. Neutron mass = 1.6750 e -27 kg <br> <br> | *3. Neutron mass = 1.6750 e -27 kg <br> <br> | ||
''' | Because of revolutions in modern physics in the last two centuries, we know that these particles act differently than objects in the macroscopic world. In fact, any object that can move close to the speed of light will behave differently than most objects we encounter in our daily life. Thus, we have unique ways of calculating the energies associated with subatomic particles. | ||
===Types of Energy=== | |||
Every subatomic particle has two types of energy: | |||
*1. Rest energy | |||
**- energy of a particle's mass when at rest | |||
*2. Kinetic energy | |||
**- energy associated with a particle's motion | |||
Lucky for you, the actual process of calculating these quantities is quite simple. You just need to pay attention to the wording of a given question and units! | |||
===The Lorentz Factor (γ)=== | |||
The formulae for rest energy and kinetic energy of subatomic particles correlate obviously with the formulae for the energy of macroscopic quantities. The only notable change is the presence of γ (gamma), also known as the Lorentz Factor. | |||
The Lorentz Factor is used when particles are moving at a '''speed close to the speed of light''' (represented as 'c'). At these extremely high speeds, it is necessary to also make '''relativistic corrections''' to our calculations of energy. | |||
As you can see below, as the ratio of the particle speed to the speed of light approaches zero (in other words, as the particle speed becomes closer to the speed of light), γ approaches 1. Then, the energy formulae look exactly like the ones you're used to! | |||
[[File:Relativisticenergy.gif|center|frame|Relativistic Energy Equations <br> (see ref. 1)]] | |||
== A Mathematical Model == | |||
There are four equations that encompass and represent this phenomenon: | |||
=== 1. Relativistic Correction (Lorentz) Factor === | |||
<math>γ = 1/ \sqrt{1-(v^2/c^2)}</math> | |||
where v is the particle's velocity and c is the speed of light, 3 x 10^8 m/s. <br> | |||
=== 2. Rest Energy of a Particle (the famous one) === | |||
[[File:Bow and Arrow Right Side.gif|thumb|Bow and Arrow Right Side]] | |||
<math> E_{Rest}=mc^2 </math> | |||
where <b>m</b> is the mass and <b>c</b> is the speed of light. | |||
Rest energy is the energy inherently contained by a particle because of its chemical makeup. Thus, rest energy can only change if the system being observed is at such an atomic level where particles can change identities/composition spontaneously during interactions with surroundings. <br> | |||
[[File:Albert Einstein near a blackboard with special relativity formulae, before 1940.jpg|thumb|Albert Einstein near a blackboard with special relativity formulae, before 1940]] | |||
=== 3. Kinetic Energy of a Particle Nearing the Speed of Light=== | |||
<math> E_{Kinetic}=γmc^2-mc^2 </math> | |||
<math> E_{Particle}=γmc^2</math> <br> | were γ is rest energy (as calculated in 1.), m is the particle's mass, and c is the speed of light <br> | ||
[[File:Speed of light from Earth to Moon.gif|thumb|Speed of light from Earth to Moon]] | |||
=== 4. Combined Energy Equation=== | |||
<math> E_{Particle}=γmc^2</math> <br> | |||
where γ is as calculated above, m is the particle's mass and c is the speed of light | |||
== A Computational Model == | == A Computational Model == | ||
Often, such computational models will be helpful to check your work and can be expanded to even provide helpful visualizations of your particles. | |||
As per usual, be very careful about units and review your Vpython syntax! | |||
Common mistakes include using '**' instead of '*'. 'x**y' indicates raising x to the power of y, where as 'x*y' indicates multiplying x and y. | |||
[[File:glowscript.png]] | |||
Try it out yourself! | |||
Make a copy of this starter code: https://www.glowscript.org/#/user/samyukta/folder/MyPrograms/program/testablerelativistic | |||
== Examples == | == Examples == | ||
=== Simple === | |||
A neutron moves at 98% of the speed of light. What is its momentum? | |||
1. We know that normally, momentum is given as p = mv. However, since the particle is moving at a speed very close to the speed of light, we infer that we need to use relativistic momentum, p = mγv | |||
2. v = 0.98(3e8) = 294000000 m/s | |||
3. mass of a neutron = 1.6750e-27 | |||
4. <math>γ = 1/ \sqrt{1-(v^2/c^2)}</math> = <math>γ = 1/ \sqrt{1-((294000000)^2/(3e8)^2)}</math> = 5.025 | |||
5. Therefore, p = (1.6750e-27)(5.025)(294000000) = -3.316e10 kg*m/s | |||
=== Middling === | |||
A proton moves at 0.950c. | A proton moves at 0.950c. | ||
Calculate its (a) rest energy, (b) total energy, and (c) kinetic energy. | Calculate its (a) rest energy, (b) total energy, and (c) kinetic energy. | ||
*(a) <math> E_{rest}=mc^2 </math> = (1.67e-27 kg)(3e8 m/s)^2 = 1.5e-10 J | *(a) <math> E_{rest}=mc^2 </math> = (1.67e-27 kg)(3e8 m/s)^2 = 1.5e-10 J | ||
| Line 52: | Line 102: | ||
*(c) <math> K=γmc^2-mc^2 </math> = 4.81e-10 J - 1.50e-10 J = 3.31e-10 J | *(c) <math> K=γmc^2-mc^2 </math> = 4.81e-10 J - 1.50e-10 J = 3.31e-10 J | ||
=== Difficult === | |||
An electron is accelerated to a speed of 2.95 × 10<sup>8</sup> ( | An electron is accelerated to a speed of 2.95 × 10<sup>8</sup> | ||
a) What is the energy of the electron? | (a) What is the energy of the electron? | ||
(b) What is the rest energy of the electron? | (b) What is the rest energy of the electron? | ||
(c) What is the kinetic energy of the moving proton? | (c) What is the kinetic energy of the moving proton? | ||
(a) <br> | (a) <br> | ||
E = γmc<sup>2</sup> <br> | E = γmc<sup>2</sup> <br> | ||
E = (5.50)(9.11 × 10<sup>-31</sup>)(3 × 10<sup>8</sup>) <br> | E = (5.50)(9.11 × 10<sup>-31</sup>)(3 × 10<sup>8</sup>) <br> | ||
E = 1.50 × 10<sup>-21</sup> J<br> | E = 1.50 × 10<sup>-21</sup> J<br> | ||
| Line 72: | Line 123: | ||
== Connectedness == | == Connectedness == | ||
As a biomedical engineering student, although it might seem far-fetched, concepts like relativity are important when we consider the implications of nanotechnology and particularly, nanomedicine to the human body. Understanding the nuances of drug delivery rates and chemical movement is critical to developing new treatments and therapies that are safe, efficient, and effective, and these chemical, and submolecular interactions and activities can be simplified to physics at a fundamental scale. | |||
In real life, relativity is a critical part of how we develop and improve electrical generators and transformers, as the success of these devices depends on the strategic coordinated movement of electrons. Similarly, magnetism is based on relativity and the interactions of point particles of opposite and like charges, and so many devices and modern research equipment are based fundamentally on the correct operation of magnetism, such as the ubiquitous Global Positioning System, or GPS. | |||
[[File:Oscillograph and generator.jpg|thumb|Oscillograph and generator]] | |||
1. How does modern relativity modify the law of conservation of energy? | |||
According to modern relativity, the relativistic momentum of a particle can be defined as p = γmv for velocities that are near the speed of light. This is also the same thing as multiplying classical momentum, p = mv, by the relativistic factor γ. Relativistic momentum approaches infinity as the particle’s speed approaches c, the speed of light. This indicates that a particle will never reach the exact speed of light no matter how close it can get to it. This prevents its momentum from becoming infinite. As it is seen from the graph, as v approaches c, the momentum value goes to positive infinity, but never actually becomes infinity, which proves the law of conservation of momentum true. If the momentum value had reached infinity, then we wouldn’t be able to make a conclusion about the conservation of momentum. Thus, we would also be unable to make a claim about the conservation of energy since it is related to momentum. | |||
[[File:momentumspeed.jpg|350px|thumb|right|Momentum vs. Speed Graph]] | |||
2. Is it possible for an external force to be acting on a system and for relativistic momentum to be conserved? Explain. | |||
Even if there is an external force acting on a system, if there are additional external forces that balance this force out, the net external force will be zero, and the relativistic momentum will be conserved. If the net external force is zero, this means that the acceleration of the system will also be zero. Zero acceleration means that the initial and final values for the velocity of the system are the same. This leads to a momentum value that does not change throughout the process, assuming that the mass of the system is kept the same. In this case, we can conclude that if there is an external force acting on a system, the relativistic momentum can still be conserved as long as the net external force is zero. | |||
3. Given the fact that light travels at c, can it have mass? Explain. | |||
We know that c, the speed of light, is equal to 3E10^8 m/s. According to Maxwell’s equation, any object with mass m cannot travel with the speed of light or greater. Therefore, we conclude that if light travels at c, then it should not have a mass. | |||
4. We know that the velocity of an object with mass has an upper limit of c. Is there an upper limit on its momentum? Its energy? Explain. | |||
Neither the momentum nor the energy has an upper limit. The relativistic momentum is given by p = γmu, and the total energy is given by E = γmc^2. We know that γ approaches infinity as v approaches the speed of light, c. Looking at the equations, we see that γ is directly proportional to both momentum and total energy. As γ tends to infinity, momentum and total energy tend to infinity as well. Therefore, it can be concluded that there is no upper limit to either of them. | |||
== History == | == History == | ||
[[File:einstein1.jpg|350px|thumb|left|Albert Einstein]] | |||
E = mc^2 is probably the most popular formula in the world of physics. This formula has been printed on countless shirts as well as shared on social media in various contexts. Now it is time to learn where did this formula actually come from? | |||
This formula was first submitted by Nobel laureate Albert Einstein on September 27, 1905. In his paper called “Does the Inertia of a Body Depend Upon Its Energy Content?”, Einstein first explained the photoelectric effect and experimentally proved the existence of atoms. Then, he set down the relationship between energy (E) and mass (m) in a way that has never been seen before. His formula showed a new way to relate the motions of objects in the universe, which is also known as special relativity. Before Einstein introduced this equation, mass was known only as a quantity to measure the presence of matter. However, with this new equation, the mass turned into a way to measure the total energy of an object even if it is motionless. Time and space, and mass and energy were no longer separate. The notation E = mc^2 revealed connections in nature that originated other ground-breaking outcomes, such as the win paradox, and it also associated Einstein’s name with genius. | |||
[[File:Wörgl, Gedenkplatte A Einstein, 1.jpeg|thumb|Wörgl, Gedenkplatte A Einstein, 1]] | |||
== | == Further Reading == | ||
(1) http://spiff.rit.edu/classes/phys150/lectures/ke_rel/ke_rel.html | (1) http://spiff.rit.edu/classes/phys150/lectures/ke_rel/ke_rel.html | ||
(2) http://www.desy.de/user/projects/Physics/Relativity/GR/energy_gr.html | |||
(3) http://acme.highpoint.edu/~atitus/phy221/lecture-notes/7-2-particle-energy.pdf | |||
(4) https://engagedscholarship.csuohio.edu/cgi/viewcontent.cgi?article=1071&context=tdr | |||
(5) https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5253894/ | |||
==External Links== | |||
(1) https://www.livescience.com/58245-theory-of-relativity-in-real-life.html | |||
(2) https://www.nationalgeographic.com/science/article/beyond-einstein | |||
== References == | |||
(1) http://www.desy.de/user/projects/Physics/Relativity/GR/energy_gr.html | |||
(2) http://acme.highpoint.edu/~atitus/phy221/lecture-notes/7-2-particle-energy.pdf | |||
(3) https://www.livescience.com/58245-theory-of-relativity-in-real-life.html | |||
(4) https://www.nationalgeographic.com/science/article/beyond-einstein | |||
(5) http://spiff.rit.edu/classes/phys150/lectures/ke_rel/ke_rel.html | |||
(6) https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5253894/ | |||
Latest revision as of 23:39, 4 December 2022
Claimed by Samyukta Iyer - Fall 2022 Elif Kulaksizoglu Fall 2019
The Main Idea
We are going to take a side step from the macroscopic world for a moment, and focus on the energy of very small (subatomic) particles, such as protons, neutrons, and electrons.
Point Particles (a closer look)

Types of point particles:
- 1. Electrons (seen as green particles in orbitals of atom)
- 2. Protons (seen as black particles in nucleus of atom)
- 3. Neutrons (seen as white particles in nucleus of atom)
Masses of point particles:
- 1. Electron mass = 9.109 e -31 kg
- 2. Proton mass = 1.6726 e -27 kg
- 3. Neutron mass = 1.6750 e -27 kg
Because of revolutions in modern physics in the last two centuries, we know that these particles act differently than objects in the macroscopic world. In fact, any object that can move close to the speed of light will behave differently than most objects we encounter in our daily life. Thus, we have unique ways of calculating the energies associated with subatomic particles.
Types of Energy
Every subatomic particle has two types of energy:
- 1. Rest energy
- - energy of a particle's mass when at rest
- 2. Kinetic energy
- - energy associated with a particle's motion
Lucky for you, the actual process of calculating these quantities is quite simple. You just need to pay attention to the wording of a given question and units!
The Lorentz Factor (γ)
The formulae for rest energy and kinetic energy of subatomic particles correlate obviously with the formulae for the energy of macroscopic quantities. The only notable change is the presence of γ (gamma), also known as the Lorentz Factor.
The Lorentz Factor is used when particles are moving at a speed close to the speed of light (represented as 'c'). At these extremely high speeds, it is necessary to also make relativistic corrections to our calculations of energy.
As you can see below, as the ratio of the particle speed to the speed of light approaches zero (in other words, as the particle speed becomes closer to the speed of light), γ approaches 1. Then, the energy formulae look exactly like the ones you're used to!
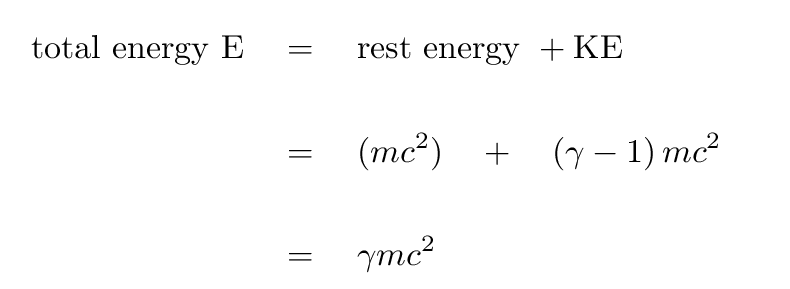
(see ref. 1)
A Mathematical Model
There are four equations that encompass and represent this phenomenon:
1. Relativistic Correction (Lorentz) Factor
[math]\displaystyle{ γ = 1/ \sqrt{1-(v^2/c^2)} }[/math]
where v is the particle's velocity and c is the speed of light, 3 x 10^8 m/s.
2. Rest Energy of a Particle (the famous one)

[math]\displaystyle{ E_{Rest}=mc^2 }[/math] where m is the mass and c is the speed of light.
Rest energy is the energy inherently contained by a particle because of its chemical makeup. Thus, rest energy can only change if the system being observed is at such an atomic level where particles can change identities/composition spontaneously during interactions with surroundings.

3. Kinetic Energy of a Particle Nearing the Speed of Light
[math]\displaystyle{ E_{Kinetic}=γmc^2-mc^2 }[/math]
were γ is rest energy (as calculated in 1.), m is the particle's mass, and c is the speed of light

4. Combined Energy Equation
[math]\displaystyle{ E_{Particle}=γmc^2 }[/math]
where γ is as calculated above, m is the particle's mass and c is the speed of light
A Computational Model
Often, such computational models will be helpful to check your work and can be expanded to even provide helpful visualizations of your particles. As per usual, be very careful about units and review your Vpython syntax!
Common mistakes include using '**' instead of '*'. 'x**y' indicates raising x to the power of y, where as 'x*y' indicates multiplying x and y.
 Try it out yourself!
Make a copy of this starter code: https://www.glowscript.org/#/user/samyukta/folder/MyPrograms/program/testablerelativistic
Try it out yourself!
Make a copy of this starter code: https://www.glowscript.org/#/user/samyukta/folder/MyPrograms/program/testablerelativistic
Examples
Simple
A neutron moves at 98% of the speed of light. What is its momentum?
1. We know that normally, momentum is given as p = mv. However, since the particle is moving at a speed very close to the speed of light, we infer that we need to use relativistic momentum, p = mγv 2. v = 0.98(3e8) = 294000000 m/s 3. mass of a neutron = 1.6750e-27 4. [math]\displaystyle{ γ = 1/ \sqrt{1-(v^2/c^2)} }[/math] = [math]\displaystyle{ γ = 1/ \sqrt{1-((294000000)^2/(3e8)^2)} }[/math] = 5.025 5. Therefore, p = (1.6750e-27)(5.025)(294000000) = -3.316e10 kg*m/s
Middling
A proton moves at 0.950c. Calculate its (a) rest energy, (b) total energy, and (c) kinetic energy.
- (a) [math]\displaystyle{ E_{rest}=mc^2 }[/math] = (1.67e-27 kg)(3e8 m/s)^2 = 1.5e-10 J
- (b) [math]\displaystyle{ E_{particle}=γmc^2 }[/math] = (1.5e-10 J)/((1-(0.950c/c)^2)^(1/2)) = 4.81e-10 J
- (c) [math]\displaystyle{ K=γmc^2-mc^2 }[/math] = 4.81e-10 J - 1.50e-10 J = 3.31e-10 J
Difficult
An electron is accelerated to a speed of 2.95 × 108 (a) What is the energy of the electron? (b) What is the rest energy of the electron? (c) What is the kinetic energy of the moving proton?
(a)
E = γmc2
E = (5.50)(9.11 × 10-31)(3 × 108)
E = 1.50 × 10-21 J
(b)
Erest = mc2
Erest = (9.11 × 10-31)(3 × 108)2
Erest = 2.73 × 10-22 J
(c)
K = E - Erest
K = 1.50 × 10-21 - 2.73 × 10-22
K = 1.23 × 10-21 J
Connectedness
As a biomedical engineering student, although it might seem far-fetched, concepts like relativity are important when we consider the implications of nanotechnology and particularly, nanomedicine to the human body. Understanding the nuances of drug delivery rates and chemical movement is critical to developing new treatments and therapies that are safe, efficient, and effective, and these chemical, and submolecular interactions and activities can be simplified to physics at a fundamental scale.
In real life, relativity is a critical part of how we develop and improve electrical generators and transformers, as the success of these devices depends on the strategic coordinated movement of electrons. Similarly, magnetism is based on relativity and the interactions of point particles of opposite and like charges, and so many devices and modern research equipment are based fundamentally on the correct operation of magnetism, such as the ubiquitous Global Positioning System, or GPS.

1. How does modern relativity modify the law of conservation of energy?
According to modern relativity, the relativistic momentum of a particle can be defined as p = γmv for velocities that are near the speed of light. This is also the same thing as multiplying classical momentum, p = mv, by the relativistic factor γ. Relativistic momentum approaches infinity as the particle’s speed approaches c, the speed of light. This indicates that a particle will never reach the exact speed of light no matter how close it can get to it. This prevents its momentum from becoming infinite. As it is seen from the graph, as v approaches c, the momentum value goes to positive infinity, but never actually becomes infinity, which proves the law of conservation of momentum true. If the momentum value had reached infinity, then we wouldn’t be able to make a conclusion about the conservation of momentum. Thus, we would also be unable to make a claim about the conservation of energy since it is related to momentum.

2. Is it possible for an external force to be acting on a system and for relativistic momentum to be conserved? Explain.
Even if there is an external force acting on a system, if there are additional external forces that balance this force out, the net external force will be zero, and the relativistic momentum will be conserved. If the net external force is zero, this means that the acceleration of the system will also be zero. Zero acceleration means that the initial and final values for the velocity of the system are the same. This leads to a momentum value that does not change throughout the process, assuming that the mass of the system is kept the same. In this case, we can conclude that if there is an external force acting on a system, the relativistic momentum can still be conserved as long as the net external force is zero.
3. Given the fact that light travels at c, can it have mass? Explain.
We know that c, the speed of light, is equal to 3E10^8 m/s. According to Maxwell’s equation, any object with mass m cannot travel with the speed of light or greater. Therefore, we conclude that if light travels at c, then it should not have a mass.
4. We know that the velocity of an object with mass has an upper limit of c. Is there an upper limit on its momentum? Its energy? Explain.
Neither the momentum nor the energy has an upper limit. The relativistic momentum is given by p = γmu, and the total energy is given by E = γmc^2. We know that γ approaches infinity as v approaches the speed of light, c. Looking at the equations, we see that γ is directly proportional to both momentum and total energy. As γ tends to infinity, momentum and total energy tend to infinity as well. Therefore, it can be concluded that there is no upper limit to either of them.
History

E = mc^2 is probably the most popular formula in the world of physics. This formula has been printed on countless shirts as well as shared on social media in various contexts. Now it is time to learn where did this formula actually come from?
This formula was first submitted by Nobel laureate Albert Einstein on September 27, 1905. In his paper called “Does the Inertia of a Body Depend Upon Its Energy Content?”, Einstein first explained the photoelectric effect and experimentally proved the existence of atoms. Then, he set down the relationship between energy (E) and mass (m) in a way that has never been seen before. His formula showed a new way to relate the motions of objects in the universe, which is also known as special relativity. Before Einstein introduced this equation, mass was known only as a quantity to measure the presence of matter. However, with this new equation, the mass turned into a way to measure the total energy of an object even if it is motionless. Time and space, and mass and energy were no longer separate. The notation E = mc^2 revealed connections in nature that originated other ground-breaking outcomes, such as the win paradox, and it also associated Einstein’s name with genius.

Further Reading
(1) http://spiff.rit.edu/classes/phys150/lectures/ke_rel/ke_rel.html
(2) http://www.desy.de/user/projects/Physics/Relativity/GR/energy_gr.html
(3) http://acme.highpoint.edu/~atitus/phy221/lecture-notes/7-2-particle-energy.pdf
(4) https://engagedscholarship.csuohio.edu/cgi/viewcontent.cgi?article=1071&context=tdr
(5) https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5253894/
External Links
(1) https://www.livescience.com/58245-theory-of-relativity-in-real-life.html
(2) https://www.nationalgeographic.com/science/article/beyond-einstein
References
(1) http://www.desy.de/user/projects/Physics/Relativity/GR/energy_gr.html
(2) http://acme.highpoint.edu/~atitus/phy221/lecture-notes/7-2-particle-energy.pdf
(3) https://www.livescience.com/58245-theory-of-relativity-in-real-life.html
(4) https://www.nationalgeographic.com/science/article/beyond-einstein
(5) http://spiff.rit.edu/classes/phys150/lectures/ke_rel/ke_rel.html