Speed of Sound in Solids: Difference between revisions

From Physics Book
Jump to navigation Jump to search
 
(14 intermediate revisions by 2 users not shown)
Line 1: Line 1:
Claudia Tiller, Spring 2023


This page discusses calculating the speed of sound in various solids and provides examples of such calculations.
This page discusses the speed of sound in various solids, how to calculate them, and examples of such calculations.
 


==The Main Idea==
==The Main Idea==


The speed of sound is the speed that sound waves travel through a particular medium. The medium determines the speed limit. [[File:2743324.png|right|border]]Mediums are composed of particles that could be closely knit together or relatively spread apart. Also, these particles could act elastic or inelastic. The closer together the particles are to each other the faster the sound can be transferred through the medium. In comparison to air, sound travels considerably faster in solids. The factors that control the speed that sound travels in various solids is measured by the solid's density and elasticity, as these factors effect the vibrational energy of the sound.
The speed of sound can be defines as the distance travelled per a unit of time by a sound wave as it travels through an elastic medium. Elasticity refers to the ability of a body to resist distorting influence and return to its original shape when that influence is removed.  
 
With an increase in density, the space between particles in the solid decreases. The smaller distance between particles, or interatomic distance, the higher the speed. With an increase in elasticity of the atoms that make up the object, the lower the speed of sound in the object. Particles that have a high elasticity take more time to return to their place once they received vibrational energy. However, if the solid is completely inelastic then the sound cannot travel through it.
 
 
The practicality of this concept is great. Everyday humans' ears capture sound waves through the Pinna, [[File:Blausen_0330_EarAnatomy_MiddleEar.png|thumb|border|right|baseline|The inner ear.]]or the outer cartilage piece of the ear. The sound waves then travel up the ear canal and hit the ear drum, which vibrates from the sound. The vibrations travel through the inner ear and end up at the Cochlea.  The Cochlea transfers the vibrations into information that the auditory nerve can analyze. This process occurs everyday and without proper education of sound traveling through solids, such as the ear's different pieces, humans wouldn't be able to completely understand the concept completely.  
 


Factors that control the speed that sound travels in solids is measured by the solid's density and elasticity, as they affect the vibrational energy of the sound. Overall, the way the solid is composed determines the sound's speed limit through that solid.


==The Structure of Solids and Effects on Sound Travel==
Mediums are composed of particles that can be closely knit together or spread apart. Solids are characterized by an arrangement of atoms, ions, or molecules, where these components are generally locked in their positions. The particles can also be defined as elastic or inelastic. Particles that are closer to each other allow sound to be transferred quicker through the medium. Since particles that are compressed closer together allow sound to travel faster, it can be reasoned that sound travels slower in air.


With an increase in density, the space between particles in the solid decreases. The smaller distance between particles, or interatomic distance, the higher the speed. With an increase in elasticity of the atoms that make up the object, the lower the speed of sound in the object. Particles that have a high elasticity take more time to return to their place once they received vibrational energy. However, if the solid is completely inelastic then the sound cannot travel through it.


The practicality of this concept is highly applicable. The human ear captures sound waves through the outer cartilage of the ear, called the Pinna. The sound waves then travel up the ear canal and arrive at the ear drum which vibrates from the sound waves. After traveling through the inner ear, the vibrations arrive at the Cochlea. The Cochlea transfers the vibrations into information that auditory nerves can analyze.


===A Mathematical Model===
===A Mathematical Model===
Line 22: Line 20:
The speed of sound in solids <math> {V_{s}} </math> can be determined by the equation. Young's Modulus is a measure of elasticity of an object, and it can be computed to solve for interatomic values, such as interatomic bond stiffness or interatomic bond length.   
The speed of sound in solids <math> {V_{s}} </math> can be determined by the equation. Young's Modulus is a measure of elasticity of an object, and it can be computed to solve for interatomic values, such as interatomic bond stiffness or interatomic bond length.   


<math> {V_{s}} = d \cdot \sqrt(K_{s}/m_{atom}) </math>
<math> {V_{s}} = d \cdot \sqrt{\frac{K_{s}}{m_{atom}}} </math>


Alternative speed equation:
Alternative speed equation:


<math> {V_{s}} =  \sqrt (B/ρ) </math>
<math> {V_{s}} =  \sqrt{\frac{B}{\rho}} </math>


<math> ρ </math> = density
<math> ρ </math> = density
Line 58: Line 56:
Solution: In this situation, the ratio of the speed of sound in rod A to the speed of sound in rod B is 1.  
Solution: In this situation, the ratio of the speed of sound in rod A to the speed of sound in rod B is 1.  


Looking at the formula for computing speed of sound in solids, <math> {V_{s}} = d* √ (K_{s}/m_{atom}) </math>, you see that velocity depends three factors, interatomic stiffness, the mass of one atom, and interatomic bond length. The two rods differences in atomic mass and interatomic stiffness offset each other when the equations are set equal, and the ratio is determined to be 1.
Looking at the formula for computing speed of sound in solids, <math> {V_{s}} = d \cdot \sqrt{\frac{K_{s}}{m_{atom}}} </math>, you see that velocity depends three factors, interatomic stiffness, the mass of one atom, and interatomic bond length. The two rods differences in atomic mass and interatomic stiffness offset each other when the equations are set equal, and the ratio is determined to be 1.


<math>  d* √ 4(K_{s}/m_{atom}) =  d* √ (K_{s}/4m_{atom}) </math>    After simplification <math> V_{s_{1}} = V_{s{2}} </math>
<math>  d \cdot \sqrt{\frac{4 \cdot K_{s}}{m_{atom}}} =  d \cdot \sqrt{\frac{4 \cdot K_{s}}{m_{atom}}} </math>    After simplification <math> V_{s_{1}} = V_{s{2}} </math>


===Numerical Example ===
===Numerical Example ===
Line 74: Line 72:
Now, we have solved for both interatomic bond length and stiffness. The only quantity in the final speed of sound equation we need is the mass of one atom, which can be determined using Avogardro's number and the atomic mass. <math> m_{atom} = </math> ''atomic mass'' / <math> 6.022e23 </math>
Now, we have solved for both interatomic bond length and stiffness. The only quantity in the final speed of sound equation we need is the mass of one atom, which can be determined using Avogardro's number and the atomic mass. <math> m_{atom} = </math> ''atomic mass'' / <math> 6.022e23 </math>


Now that all variables are solved for, we can substitute values into our <math> {V_{s}} = d* √ (K_{s}/m_{atom}) </math> equation.  
Now that all variables are solved for, we can substitute values into our <math> {V_{s}} = d \cdot \sqrt{\frac{K_{s}}{m_{atom}}} </math> equation.  


<math> {V_{s}} = 1.6e-10* √ (78534.7/1.79e-22) </math>
<math> {V_{s}} = 1.6 \cdot 10^{-10} \cdot \sqrt{ \frac{78534.7}{1.79 \cdot 10^{-22}}} </math>


<math> {V_{s}} = 2723</math> m/s
<math> {V_{s}} = 2723</math> m/s


==Connectedness==
==Connectedness==
The computation of speed of sound in solids is dependent on a mass' interatomic properties, such as interatomic bond length. I find it interesting when a object's interatomic properties determine its functionality on a larger scale. In the case of speed of sound in solids, the objects elasticity depends on the interatomic bond length.  
Computing the speed of sound in solids depends on a mass' interatomic properties, such as interatomic bond length. In this specific case, an object's elasticity depends on the interatomic bond length. There are many applications that connect to the ability to compute the speed of sounds. 


While the computation of speed of sound in solids may not seem related to Industrial Engineering, it has clear implications in the process of choosing building materials, which is a notable section of industrial engineering. For example, if you are planning to build something soundproof, it would be optimal to choose a solid with a very low speed of sound velocity.  
Seismic and ultrasonic imaging are also fields that benefit greatly from the calculation of sound speeds in solids. Seismic imaging refers to capturing images of the subsurface structure of the Earth. Seismic waves can be generated by earthquakes or other sources. Engineers and scientists can then locate gas and oil reservoirs, monitor activity such as volcano eruptions, and geological formations. In ultrasonic imaging, ultrasonic waves can be sent through the body and have the time it takes to bounce back be measured. This then creates images of internal organs or tissues, used in cases such as prenatal imaging as well as medical diagnosing. In more specific fields such as in Industrial Engineering, these calculations could be applied to questions regarding how to build a soundproof area. It would therefore be optimal to select a solid with a low speed of sound velocity, with a solid that has tightly packed particles. There are many vast applications to this, as an object's ability to block or allow sound waves through it. However, some cases require contractors to build structures that allow sound to travel through. Material testing uses the calculation of sound in solids to determine mechanical properties of such materials. Engineers can then calculate the material's elasticity, stiffness, and other properties. Knowledge regarding how solids are structured and how they correlate with the speed of sounds in those solids are vital to building structures that meet the criteria.


The industrial applications in terms of construction are vast. An objects ability to block/allow sound waves through it is very important. Of course, insulation materials and sound proof wall materials come to thought at first. However, in some cases, contractors need to build structures that allow sound to travel through, in which they would choose solid materials that correlate with high speeds of sound.
Overall, being able to calculate the speed of sounds in solids has a wide range of applications in engineering, medicine, and science.


==History==
==History==

Latest revision as of 15:21, 17 April 2023

Claudia Tiller, Spring 2023

This page discusses the speed of sound in various solids, how to calculate them, and examples of such calculations.

The Main Idea

The speed of sound can be defines as the distance travelled per a unit of time by a sound wave as it travels through an elastic medium. Elasticity refers to the ability of a body to resist distorting influence and return to its original shape when that influence is removed.

Factors that control the speed that sound travels in solids is measured by the solid's density and elasticity, as they affect the vibrational energy of the sound. Overall, the way the solid is composed determines the sound's speed limit through that solid.

The Structure of Solids and Effects on Sound Travel

Mediums are composed of particles that can be closely knit together or spread apart. Solids are characterized by an arrangement of atoms, ions, or molecules, where these components are generally locked in their positions. The particles can also be defined as elastic or inelastic. Particles that are closer to each other allow sound to be transferred quicker through the medium. Since particles that are compressed closer together allow sound to travel faster, it can be reasoned that sound travels slower in air.

With an increase in density, the space between particles in the solid decreases. The smaller distance between particles, or interatomic distance, the higher the speed. With an increase in elasticity of the atoms that make up the object, the lower the speed of sound in the object. Particles that have a high elasticity take more time to return to their place once they received vibrational energy. However, if the solid is completely inelastic then the sound cannot travel through it.

The practicality of this concept is highly applicable. The human ear captures sound waves through the outer cartilage of the ear, called the Pinna. The sound waves then travel up the ear canal and arrive at the ear drum which vibrates from the sound waves. After traveling through the inner ear, the vibrations arrive at the Cochlea. The Cochlea transfers the vibrations into information that auditory nerves can analyze.

A Mathematical Model

The speed of sound in solids [math]\displaystyle{ {V_{s}} }[/math] can be determined by the equation. Young's Modulus is a measure of elasticity of an object, and it can be computed to solve for interatomic values, such as interatomic bond stiffness or interatomic bond length.

[math]\displaystyle{ {V_{s}} = d \cdot \sqrt{\frac{K_{s}}{m_{atom}}} }[/math]

Alternative speed equation:

[math]\displaystyle{ {V_{s}} = \sqrt{\frac{B}{\rho}} }[/math]

[math]\displaystyle{ ρ }[/math] = density

[math]\displaystyle{ B }[/math] = Bulks Modulus

Bulks Modulus = [math]\displaystyle{ {\frac {ΔP}{ΔV/V}} }[/math]

[math]\displaystyle{ d }[/math] = interatomic bond length

[math]\displaystyle{ K_{s} }[/math] = Interatomic bond stiffness

Youngs Modulus = ([math]\displaystyle{ Y = K_{s}/d }[/math])

Youngs Modulus: [math]\displaystyle{ Y ={\frac{Stress}{Strain}} }[/math]

[math]\displaystyle{ Stress = {\frac{F_{tension}}{Area_{Cross Sectional}}} }[/math]

[math]\displaystyle{ Strain = {\frac{ΔL_{wire}}{L_{0}}} }[/math]

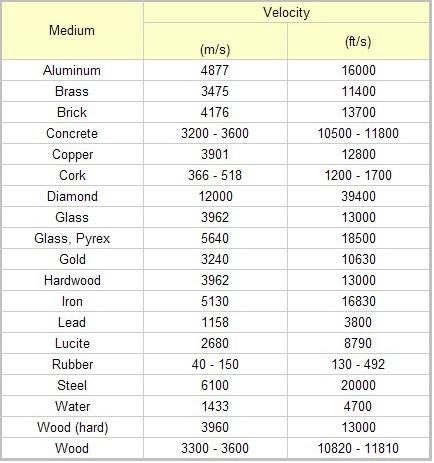
Speeds of Various Compositions

Examples

Theoretical

Two metal rods are made of different elements. The interatomic spring stiffness of element A is four times larger than the interatomic spring stiffness for element B. The mass of an atom of element A is four times greater than the mass of an atom of element B. The atomic diameters are approximately the same for A and B. What is the ratio of the speed of sound in rod A to the speed of sound in rod B?

Solution: In this situation, the ratio of the speed of sound in rod A to the speed of sound in rod B is 1.

Looking at the formula for computing speed of sound in solids, [math]\displaystyle{ {V_{s}} = d \cdot \sqrt{\frac{K_{s}}{m_{atom}}} }[/math], you see that velocity depends three factors, interatomic stiffness, the mass of one atom, and interatomic bond length. The two rods differences in atomic mass and interatomic stiffness offset each other when the equations are set equal, and the ratio is determined to be 1.

[math]\displaystyle{ d \cdot \sqrt{\frac{4 \cdot K_{s}}{m_{atom}}} = d \cdot \sqrt{\frac{4 \cdot K_{s}}{m_{atom}}} }[/math] After simplification [math]\displaystyle{ V_{s_{1}} = V_{s{2}} }[/math]

Numerical Example

The Young's Modulus value of silver is 7.75e+10, atomic mass of silver is 108 g/mole, and the density of silver is 10.5 g/cm3. Using this information, calculate the speed of sound in silver.

Solution: The key to solving this problem is to realize the micro-macro connection of Young's Modulus. You are given that Young's Modulus is equal to 7.75e+10, and we know that Youngs Modulus = ([math]\displaystyle{ K_{s}/d }[/math]). In this situation, we need to calculate the interatomic bond length and use it and our Young's Modulus value to determine our interatomic stiffness.

To solve for d, we use the given density of silver (10.5 g/cm3). Using the basic equation for volume in relation to density and mass ([math]\displaystyle{ V=m*d }[/math]), we can find d, since d is equal to the cube root of volume.

Once d is solved for, it can be plugged back into the the equation [math]\displaystyle{ Y = K_{s}/d }[/math] to solve for [math]\displaystyle{ K_{s} }[/math]

Now, we have solved for both interatomic bond length and stiffness. The only quantity in the final speed of sound equation we need is the mass of one atom, which can be determined using Avogardro's number and the atomic mass. [math]\displaystyle{ m_{atom} = }[/math] atomic mass / [math]\displaystyle{ 6.022e23 }[/math]

Now that all variables are solved for, we can substitute values into our [math]\displaystyle{ {V_{s}} = d \cdot \sqrt{\frac{K_{s}}{m_{atom}}} }[/math] equation.

[math]\displaystyle{ {V_{s}} = 1.6 \cdot 10^{-10} \cdot \sqrt{ \frac{78534.7}{1.79 \cdot 10^{-22}}} }[/math]

[math]\displaystyle{ {V_{s}} = 2723 }[/math] m/s

Connectedness

Computing the speed of sound in solids depends on a mass' interatomic properties, such as interatomic bond length. In this specific case, an object's elasticity depends on the interatomic bond length. There are many applications that connect to the ability to compute the speed of sounds.

Seismic and ultrasonic imaging are also fields that benefit greatly from the calculation of sound speeds in solids. Seismic imaging refers to capturing images of the subsurface structure of the Earth. Seismic waves can be generated by earthquakes or other sources. Engineers and scientists can then locate gas and oil reservoirs, monitor activity such as volcano eruptions, and geological formations. In ultrasonic imaging, ultrasonic waves can be sent through the body and have the time it takes to bounce back be measured. This then creates images of internal organs or tissues, used in cases such as prenatal imaging as well as medical diagnosing. In more specific fields such as in Industrial Engineering, these calculations could be applied to questions regarding how to build a soundproof area. It would therefore be optimal to select a solid with a low speed of sound velocity, with a solid that has tightly packed particles. There are many vast applications to this, as an object's ability to block or allow sound waves through it. However, some cases require contractors to build structures that allow sound to travel through. Material testing uses the calculation of sound in solids to determine mechanical properties of such materials. Engineers can then calculate the material's elasticity, stiffness, and other properties. Knowledge regarding how solids are structured and how they correlate with the speed of sounds in those solids are vital to building structures that meet the criteria.

Overall, being able to calculate the speed of sounds in solids has a wide range of applications in engineering, medicine, and science.

History

The speed of sound in air was first measured by Sir Isaac Newton, and first correctly computed by Pierre-Simon Laplace in 1816. Before this precise measurement, attempts had been made across Europe during the 1700s, most famously Reverend William Derham's experiment in 1709 across the town of Upminister, England. Reverend Derham used a shotgun's noise and several known landmarks around time to measure the time it took for the sound of the blast to be heard from select distances.

Young's Modulus was named after English physicist Thomas Young. In actuality, the concept was developed earlier by physicists Leonhard Euler and Giordano Riccati in the 1720s.

See also

Youngs Modulus: [1] Interatomic Bonds: [2]

Further reading

Further Information can be found on the speed of sound in solids in Matter and Interactions, 4th Edition by Ruth W. Chabay & Bruce A. Sherwood

External links

Internet resources on this topic can be found at:

Engineering Tool Box [3]

Hyperphysics [4]

Potto Project [5]

NDT Resource Center [6]

The Engineering ToolBox [7]

Ear Image [8]

Yew Chung [9]

References

This section contains the the references used while writing this page

Chart from [10]

Matter and Interactions 4th Edition by Chabay and Sherwood

Wikipage created by Daiven Patel

Retrieved from "http://www.physicsbook.gatech.edu/index.php?title=Speed_of_Sound_in_Solids&oldid=41802"