Charged Ring: Difference between revisions
No edit summary |
|||
| (63 intermediate revisions by 8 users not shown) | |||
| Line 1: | Line 1: | ||
<strong>Additinal Edits by George Sorkin, Spring 2024</strong> | |||
==The Main Idea== | ==The Main Idea== | ||
Charges may be arranged in a variety of ways. When points are uniformly distributed a finite distance away from some point, which we define as the origin, we call this curve as a ring. We can position a [[Point Charge]] at every point upon this ring. To analyze this continuous arrangement of charges, we say that their individual contributions are infinitesimally small, and then sum each of these contributions together to arrive at the electric field produced by this charge distribution. | Charges may be arranged in a variety of ways. When points are uniformly distributed a finite distance away from some point, which we define as the origin, we call this curve as a ring. We can position a [[Point Charge]] at every point upon this ring. To analyze this continuous arrangement of charges, we say that their individual contributions are infinitesimally small, and then sum each of these contributions together to arrive at the electric field produced by this charge distribution. We can compute the net electric field of this charge distribution with Coulomb's Law and by applying integration principles. The ring field can also be used to calculate the electric field of a [[Charged Disk]]. | ||
===A Mathematical Model=== | ===A Mathematical Model=== | ||
This mathematical model is based | This mathematical model is based on the individual [[Electric Field]] contributions of a number of point charges, each of which is defined by | ||
<math>\vec{E} = \frac{1}{4\pi\epsilon_{0}}\frac{q}{|\vec{r}|^{2}}\hat{r}</math>. | <math>\vec{E} = \frac{1}{4\pi\epsilon_{0}}\frac{q}{|\vec{r}|^{2}}\hat{r}</math>. | ||
'''Do not forget this equation'''. This equation must be memorized as it isn't given on the formula sheet. | |||
We also say that this vector field is a member of a linear space of vectors. This is to say that we can apply the [[Superposition Principle]] meaning that we can sum any number of these electric field vectors and obtain another vector which is the electric field vector contributed by those charges. When we continuously sum all of the vectors produced by these charges, we get the electric field produced by the entire arrangement of charges. | We also say that this vector field is a member of a linear space of vectors. This is to say that we can apply the [[Superposition Principle]] meaning that we can sum any number of these electric field vectors and obtain another vector which is the electric field vector contributed by those charges. When we continuously sum all of the vectors produced by these charges, we get the electric field produced by the entire arrangement of charges. | ||
[[File:red_ring.png|400px|thumb|Figure 1: diagram of a charged ring]] | |||
The diagram above shows the electric field due to one infinitesimal piece of the ring, <math>dq</math>. In order to avoid rigorous computations, we can see that the electric field of the charges cancels out in the vertical direction. Only the horizontal component will remain. For an observation location that is on the symmetry axis as the ring, the other two components will be zero. If the observation location were off axis, then it would be very different requiring more math. Since each piece, <math>dq</math>, contributes a <math>d\vec{E}</math> of <math>\frac{1}{4\pi\epsilon_{0}}\frac{dq}{|\vec{d}|^{2}}\hat{d}</math>, we can compute the horizontal component by multiplying the magnitude of <math>d\vec{E}</math> with <math>\cos{θ}</math>. | |||
<math>|d\vec{E}_{z}| = \frac{1}{4\pi\epsilon_{0}}\frac{dq}{r^2 + z^2}\cos{θ} = \frac{1}{4\pi\epsilon_{0}}\frac{dq}{r^2 + z^2}\frac{z}{(r^2 + z^2)^\frac{1}{2}}</math> | |||
Now we integrate to sum all the electric field contributions of each infinitesimal <math>dq</math>. | |||
<math>\vec{E}_{z} = \frac{1}{4\pi\epsilon_{0}}\frac{z}{(r^2 + z^2)^\frac{3}{2}}\int_{}^{} dq = \frac{1}{4\pi\epsilon_{0}}\frac{Qz}{(r^2 + z^2)^\frac{3}{2}}</math> | |||
As a reminder, this is the equation given on the formula sheet. It '''only''' works when the location at which the field is being measured is along the <math>{z}</math> axis. However, the equation for it being off axis is not given on the equation sheet. That requires a separate and more difficult integration. Typically, the only way this would be asked on a test is to set up an equation that would be integrated that requires you to find a new <math>dQ</math>. | |||
'''Rigorous Derivation''' | |||
1. Define shape characteristics of the ring | |||
:The ring has some finite charge. | |||
:We see that this arrangement is circular, so a coordinate system with which we can define radial and angular coordinates would be useful. Naturally, this would be the polar coordinate system. | |||
:We also see that all charge is uniformly distributed some finite distance R from the center of the ring. It would be useful to let the center of the ring be the origin of our coordinate axes. | |||
:Here is a reasonable arrangement for this charged ring. | |||
[[File:blue_graph.png|400px|thumb|Figure 2: defining a coordinate system about a charged ring]] | |||
:Since all charge is concentrated upon the edge of the circle, we can consider our charge distribution to be invariant with respect to radial distance. However, we do see that our charge distribution is the function of theta. | |||
2. Compute charge distribution function | |||
:Let us call the charge distribution as <math display="inline">\sigma</math> | |||
:We have a charge distributed on the edge of the circle, so | |||
:<math> \sigma=\frac{Q}{2\pi} </math> | |||
:where <math display="inline">Q</math> represents the charge of the ring. | |||
:What this equation means is that the charge is uniformly distributed along each unit of angular length. In this way, it is called angular charge density. | |||
3. Compute infinitesimal charge contribution | |||
:Let us consider an infinitesimal section of the ring which contains exactly one point charge. The dimension of this section is given by <math display="inline">d\theta</math> which is the infinitesimal angular size. So, the infinitesimal charge contribution, <math display="inline">dQ</math>, is | |||
:<math> dQ = \frac{Q}{2\pi}d\theta </math> | |||
4. Compute infinitesimal electric field contribution | |||
:Let us define some arbitrary location at which we are observing this ring of charge. | |||
:<math> \vec{r} = x\hat{x}+y\hat{y} + z\hat{z} </math> | |||
:in polar coordinates, we see this becomes | |||
:<math> \vec{r} = Rcos(\theta)\hat{x} + Rsin(\theta)\hat{y} + z\hat{z} </math>. | |||
:Recall that both sine and cosine are periodic with the period of <math>2\pi </math>. This will become important later. | |||
:The magnitude of this vector is | |||
:<math> |\vec{r}| = \sqrt{R^{2}+z^{2}} </math> | |||
:owing to the usage of the Pythagorean trigonometric identity. | |||
:Now, we have what we need to write the electric field vector contributed by each piece of the ring of charge. Let this vector field piece be <math display="inline">d\vec{E}</math>. | |||
:<math> d\vec{E}=\frac{1}{4\pi\epsilon_{0}}\frac{q}{|\vec{r}|^{2}}\hat{r}=\frac{1}{4\pi\epsilon_{0}}\frac{dQ}{(R^{2}+z^{2})^{3/2}}(Rcos(\theta)\hat{x}+Rsin(\theta)\hat{y}+z\hat{z}) </math> | |||
5. Compute electric field vector | |||
:So, now all that is left is to sum everything up. We are summing over the circumference of a circle, so our path is defined by <math display="inline">0\leq\theta\leq 2\pi </math>. Let us now set up our integral. | |||
:<math>\vec{E}=\int_{0}^{2\pi}\frac{1}{4\pi\epsilon_{0}}\frac{q}{|\vec{r}|^{2}}\hat{r} d\theta=\int_{0}^{2\pi}\frac{1}{4\pi\epsilon_{0}}\frac{Q}{2\pi(R^{2}+z^{2})^{3/2}}(Rcos(\theta)\hat{x}+Rsin(\theta)\hat{y}+z\hat{z})d\theta</math> | |||
:Since both sine and cosine are <math display="inline">2\pi</math> periodic functions, the <math display="inline">x</math> and <math display="inline">y</math> components of <math display="inline">\vec{E}</math> go to <math display="inline">\vec{0}</math>, which is very convenient. The result is | |||
:<math> \vec{E}=\frac{1}{4\pi\epsilon_{0}}\frac{Qz}{(z^{2}+R^{2})^{3/2}}\hat{z} </math>. | |||
''Remark'' | |||
If the path we are interested in is over a half circle, third-circle or quarter-circle, or indeed any circular section, simply adjust the bounds of integration and the charge density to the ones required by the curve of interest. | |||
===A Computational Model=== | ===A Computational Model=== | ||
[https://trinket.io/glowscript/707d492e19 This simulation | [https://trinket.io/glowscript/707d492e19 This simulation] shows the result of the computation for a ring composed of 2000 electrons. This is why the vector is pointing into the ring rather than out of the ring, which would happen for a ring composed of positively charged points. | ||
== | ===Simplified Abstract Model=== | ||
Added by GEORGE SORKIN, Spring 2024 | |||
Recall the equation we used to calculate and model the electric field caused by an electrically charged ring along the center of its axis: | |||
= | :<math> \vec{E}=\frac{1}{4\pi\epsilon_{0}}\frac{Qz}{(z^{2}+R^{2})^{3/2}}\hat{z} </math>. | ||
This electric field model is dependent upon three variables: Q (electric charge), R (radius of the ring), and z (distance away from the center of the ring). This model is correct, i.e. it is completely accurate in all situations in the perfect world. We can create a more simplified model based on this model, given certain assumptions. This section will specifically explore how we can simplify this model when we assume that the distance from the ring is significantly larger than the radius of the ring (z >> R). | |||
We see that this | We can analyze this situation intuitively with an analogy. Imagine you are holding a ring directly in front of you, a couple of inches from your face. You would clearly see that the object is, in fact, ring-shaped. No surprise here. Now imagine that the ring is a mile away from your face. In this case, you may not even see the ring since it is so far away. And if you did, the shape would seem more like a point. You would not be able to identify the ring-shape property. This analogy is identical to our assumption of our simplified model; the ring's radius is so much significantly smaller than the distance. From the observer's point of view, it seems more like a point instead of a ring. This is fundamental to our simplified model. We will treat the ring as a point charge, an object with no radius. | ||
We | We can analyze this situation logically and mathematically by exploring the extreme case: when the distance from the ring approaches infinity. Since the radius will remain finite, the scale between the distance and the radius also approaches infinity. As a result, the relative effect the radius will have on the model is essentially zero. Thus, we can completely discard the radius from our simplified model. As a result, we will only have two variables in our simplified model instead of three: Q (electric charge) and z (distance from the ring). We can derive this simplified model mathematically using limits. | ||
:<math>\vec{E}=\lim_{R\to0}\left(\frac{1}{4\pi\epsilon_{0}}\frac{Qz}{(z^{2}+R^{2})^{3/2}}\hat{z}\right) | |||
=\frac{1}{4\pi\epsilon_{0}}\frac{Qz}{(z^{2}+\lim_{R\to0}\left(R\right)^{2})^{3/2}}\hat{z} | |||
=\frac{1}{4\pi\epsilon_{0}}\frac{Qz}{(z^{2})^{3/2}}\hat{z} | |||
=\frac{1}{4\pi\epsilon_{0}}\frac{Q}{z^{2}}\hat{z} | |||
</math> | |||
[ | This simplified model is identical to the equation for the electric field of a point charge. Based on this analysis, we can conclude that if the distance is significantly larger than the radius, we can treat the ring as a point charge. [https://trinket.io/glowscript/61c2217b29 This interactive model] demonstrates this concept perfectly. When our assumption holds, the percent error between this simplified model and the original model is extremely low. | ||
==Examples== | |||
=== | ===Simple=== | ||
1.) Find the function <math>E(x)</math> that represents the magnitude of the electric field along the center axis due to a uniformly charged ring of radius 0.04 m with total charge 8 C. | |||
< | <div class="toccolours mw-collapsible mw-collapsed" style="width:800px; overflow:auto;"> | ||
<div style="font-weight:bold;line-height:1.6;">Solution</div> | |||
<div class="mw-collapsible-content"> | |||
We can use the derived formula for the electric field due to a charged ring. Only the horizontal components of the electric field will remain as the rest will cancel out. | |||
<math>E(x) = \frac{1}{4\pi\epsilon_{0}}\frac{(8 C)*x}{((0.04 m)^2 + x^2)^\frac{3}{2}}</math> | |||
</div></div> | |||
===Middling=== | |||
2.) A uniformly charged ring of radius 10.0 cm has a total charge of 91.0 µC. Find the electric field on the axis of the ring at the following distances from the center of the ring. | |||
a. 1 cm | |||
b. 5 cm | |||
c. 30 cm | |||
d. 100 cm | |||
< | <div class="toccolours mw-collapsible mw-collapsed" style="width:800px; overflow:auto;"> | ||
<div style="font-weight:bold;line-height:1.6;">Solution</div> | |||
<div class="mw-collapsible-content"> | |||
Use the derived formula, and convert the given distances into meters and the charge into Coulombs. Plug these into <math>x</math> | |||
<math>E(x) = \frac{1}{4\pi\epsilon_{0}}\frac{Q*x}{(x^2 + R^2)^\frac{3}{2}}</math> | |||
a. 8.069e6 N/C | |||
b. 29.3e6 N/C | |||
c. 7.76e6 N/C | |||
d. 8.06e5 N/C | |||
</div></div> | |||
===Difficult=== | |||
<math> | Find the electric field at a distance <math>z</math> along the center axis away from a uniformly charged semicircular ring of radius R and total charge Q. | ||
<div class="toccolours mw-collapsible mw-collapsed" style="width:800px; overflow:auto;"> | |||
<div style="font-weight:bold;line-height:1.6;">Solution</div> | |||
<div class="mw-collapsible-content"> | |||
We can tweak the same integral for a uniformly charged ring by changing the limits of integration. | |||
<math> \vec{E}=\frac{1}{4\pi\epsilon_{0}}\frac{ | <math>\vec{E}=\int_{0}^{\pi}\frac{1}{4\pi\epsilon_{0}}\frac{q}{|\vec{r}|^{2}}\hat{r} d\theta=\int_{0}^{\pi}\frac{1}{4\pi\epsilon_{0}}\frac{Q}{\pi(R^{2}+z^{2})^{3/2}}(Rcos(\theta)\hat{x}+Rsin(\theta)\hat{y}+z\hat{z})d\theta</math> | ||
<math>\vec{E} = \frac{1}{4\pi\epsilon_{0}}\frac{Q}{\pi(R^{2}+z^{2})^{3/2}}(0\hat{x}+2R\hat{y}+{\pi}z\hat{z})</math> | |||
</div></div> | |||
==Connectedness== | ==Connectedness== | ||
Edited by AYESHA AHUJA Spring 2020 | |||
The idea of charge density is somewhat analogous to the idea of the mass density, which is useful in a variety of contexts, including the computation of the center of mass, the first and second moments of mass, which are useful in statics and rigid body dynamics. Instead of computing the uniform distribution of the mass of this ring, we are computing the uniform distribution of charge. This concept is also useful in visualizing what happens within a wire in a steady state circuit. The wire can be viewed to be a continuous length of rings of charge, which act as a channel through which electrons are transported, and that the electric field of these rings of charge pushes the electrons within the wire. | The idea of charge density is somewhat analogous to the idea of the mass density, which is useful in a variety of contexts, including the computation of the center of mass, the first and second moments of mass, which are useful in statics and rigid body dynamics. Instead of computing the uniform distribution of the mass of this ring, we are computing the uniform distribution of charge. This concept is also useful in visualizing what happens within a wire in a steady state circuit. The wire can be viewed to be a continuous length of rings of charge, which act as a channel through which electrons are transported, and that the electric field of these rings of charge pushes the electrons within the wire. | ||
| Line 96: | Line 197: | ||
It is also important in the context of Maxwell's equations, specifically in Gauss's Law and in the Maxwell-Faraday equation, which are concerned with electron flux and induced fields, respectively. | It is also important in the context of Maxwell's equations, specifically in Gauss's Law and in the Maxwell-Faraday equation, which are concerned with electron flux and induced fields, respectively. | ||
==History== | |||
Added by AYESHA AHUJA SPRING 2020 | |||
The first known time when charged rings were utilized to describe electromagnetism was during Faraday’s discovery of electrical induction. To conduct his experiments, Faraday used a ring made of iron that was attached to a battery. When this makeshift circuit was turned on it manipulated a compass needle by deflecting it. He showcased an induced current in the ring. | |||
== See also == | == See also == | ||
[[Charged Rod]] | ===Further reading=== | ||
*[[Charged Rod]] | |||
*[[Charged Disk]] | |||
*[[Charged Spherical Shell]] | |||
*[[Charged Capacitor]] | |||
===External links=== | |||
*https://www.youtube.com/watch?v=80mM3kSTZcE | |||
*http://hyperphysics.phy-astr.gsu.edu/hbase/electric/elelin.html | |||
*http://www.physics.udel.edu/~watson/phys208/exercises/kevan/efield1.html | |||
== | ==References== | ||
"Electric Field on the Axis of a Ring of Charge". University of Delaware Physics Library. Adapted from Stephen Kevan's lecture on Electric Fields and Charge Distribution. April 8, 1996. http://www.physics.udel.edu/~watson/phys208/exercises/kevan/efield1.html | *"Electric Field on the Axis of a Ring of Charge". University of Delaware Physics Library. Adapted from Stephen Kevan's lecture on Electric Fields and Charge Distribution. April 8, 1996. http://www.physics.udel.edu/~watson/phys208/exercises/kevan/efield1.html | ||
Chabay, R., & Sherwood, B. (2015). Matter and Interactions (4th ed., Vol. 2, pp. 597-599). Wiley. | *Chabay, R., & Sherwood, B. (2015). Matter and Interactions (4th ed., Vol. 2, pp. 597-599). Wiley. | ||
*All images produced by the author | |||
[[Category:Electric Fields]] | [[Category:Electric Fields]] | ||
Latest revision as of 22:07, 16 April 2024
Additinal Edits by George Sorkin, Spring 2024
The Main Idea
Charges may be arranged in a variety of ways. When points are uniformly distributed a finite distance away from some point, which we define as the origin, we call this curve as a ring. We can position a Point Charge at every point upon this ring. To analyze this continuous arrangement of charges, we say that their individual contributions are infinitesimally small, and then sum each of these contributions together to arrive at the electric field produced by this charge distribution. We can compute the net electric field of this charge distribution with Coulomb's Law and by applying integration principles. The ring field can also be used to calculate the electric field of a Charged Disk.
A Mathematical Model
This mathematical model is based on the individual Electric Field contributions of a number of point charges, each of which is defined by
[math]\displaystyle{ \vec{E} = \frac{1}{4\pi\epsilon_{0}}\frac{q}{|\vec{r}|^{2}}\hat{r} }[/math].
Do not forget this equation. This equation must be memorized as it isn't given on the formula sheet.
We also say that this vector field is a member of a linear space of vectors. This is to say that we can apply the Superposition Principle meaning that we can sum any number of these electric field vectors and obtain another vector which is the electric field vector contributed by those charges. When we continuously sum all of the vectors produced by these charges, we get the electric field produced by the entire arrangement of charges.

The diagram above shows the electric field due to one infinitesimal piece of the ring, [math]\displaystyle{ dq }[/math]. In order to avoid rigorous computations, we can see that the electric field of the charges cancels out in the vertical direction. Only the horizontal component will remain. For an observation location that is on the symmetry axis as the ring, the other two components will be zero. If the observation location were off axis, then it would be very different requiring more math. Since each piece, [math]\displaystyle{ dq }[/math], contributes a [math]\displaystyle{ d\vec{E} }[/math] of [math]\displaystyle{ \frac{1}{4\pi\epsilon_{0}}\frac{dq}{|\vec{d}|^{2}}\hat{d} }[/math], we can compute the horizontal component by multiplying the magnitude of [math]\displaystyle{ d\vec{E} }[/math] with [math]\displaystyle{ \cos{θ} }[/math].
[math]\displaystyle{ |d\vec{E}_{z}| = \frac{1}{4\pi\epsilon_{0}}\frac{dq}{r^2 + z^2}\cos{θ} = \frac{1}{4\pi\epsilon_{0}}\frac{dq}{r^2 + z^2}\frac{z}{(r^2 + z^2)^\frac{1}{2}} }[/math]
Now we integrate to sum all the electric field contributions of each infinitesimal [math]\displaystyle{ dq }[/math].
[math]\displaystyle{ \vec{E}_{z} = \frac{1}{4\pi\epsilon_{0}}\frac{z}{(r^2 + z^2)^\frac{3}{2}}\int_{}^{} dq = \frac{1}{4\pi\epsilon_{0}}\frac{Qz}{(r^2 + z^2)^\frac{3}{2}} }[/math]
As a reminder, this is the equation given on the formula sheet. It only works when the location at which the field is being measured is along the [math]\displaystyle{ {z} }[/math] axis. However, the equation for it being off axis is not given on the equation sheet. That requires a separate and more difficult integration. Typically, the only way this would be asked on a test is to set up an equation that would be integrated that requires you to find a new [math]\displaystyle{ dQ }[/math].
Rigorous Derivation
1. Define shape characteristics of the ring
- The ring has some finite charge.
- We see that this arrangement is circular, so a coordinate system with which we can define radial and angular coordinates would be useful. Naturally, this would be the polar coordinate system.
- We also see that all charge is uniformly distributed some finite distance R from the center of the ring. It would be useful to let the center of the ring be the origin of our coordinate axes.
- Here is a reasonable arrangement for this charged ring.
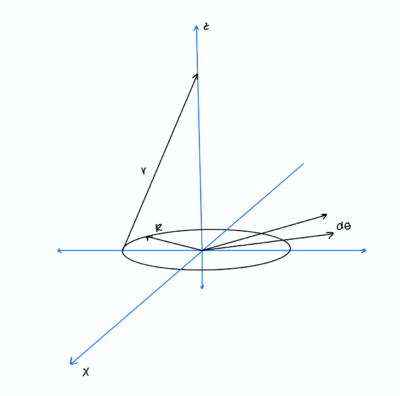
- Since all charge is concentrated upon the edge of the circle, we can consider our charge distribution to be invariant with respect to radial distance. However, we do see that our charge distribution is the function of theta.
2. Compute charge distribution function
- Let us call the charge distribution as [math]\displaystyle{ \sigma }[/math]
- We have a charge distributed on the edge of the circle, so
- [math]\displaystyle{ \sigma=\frac{Q}{2\pi} }[/math]
- where [math]\displaystyle{ Q }[/math] represents the charge of the ring.
- What this equation means is that the charge is uniformly distributed along each unit of angular length. In this way, it is called angular charge density.
3. Compute infinitesimal charge contribution
- Let us consider an infinitesimal section of the ring which contains exactly one point charge. The dimension of this section is given by [math]\displaystyle{ d\theta }[/math] which is the infinitesimal angular size. So, the infinitesimal charge contribution, [math]\displaystyle{ dQ }[/math], is
- [math]\displaystyle{ dQ = \frac{Q}{2\pi}d\theta }[/math]
4. Compute infinitesimal electric field contribution
- Let us define some arbitrary location at which we are observing this ring of charge.
- [math]\displaystyle{ \vec{r} = x\hat{x}+y\hat{y} + z\hat{z} }[/math]
- in polar coordinates, we see this becomes
- [math]\displaystyle{ \vec{r} = Rcos(\theta)\hat{x} + Rsin(\theta)\hat{y} + z\hat{z} }[/math].
- Recall that both sine and cosine are periodic with the period of [math]\displaystyle{ 2\pi }[/math]. This will become important later.
- The magnitude of this vector is
- [math]\displaystyle{ |\vec{r}| = \sqrt{R^{2}+z^{2}} }[/math]
- owing to the usage of the Pythagorean trigonometric identity.
- Now, we have what we need to write the electric field vector contributed by each piece of the ring of charge. Let this vector field piece be [math]\displaystyle{ d\vec{E} }[/math].
- [math]\displaystyle{ d\vec{E}=\frac{1}{4\pi\epsilon_{0}}\frac{q}{|\vec{r}|^{2}}\hat{r}=\frac{1}{4\pi\epsilon_{0}}\frac{dQ}{(R^{2}+z^{2})^{3/2}}(Rcos(\theta)\hat{x}+Rsin(\theta)\hat{y}+z\hat{z}) }[/math]
5. Compute electric field vector
- So, now all that is left is to sum everything up. We are summing over the circumference of a circle, so our path is defined by [math]\displaystyle{ 0\leq\theta\leq 2\pi }[/math]. Let us now set up our integral.
- [math]\displaystyle{ \vec{E}=\int_{0}^{2\pi}\frac{1}{4\pi\epsilon_{0}}\frac{q}{|\vec{r}|^{2}}\hat{r} d\theta=\int_{0}^{2\pi}\frac{1}{4\pi\epsilon_{0}}\frac{Q}{2\pi(R^{2}+z^{2})^{3/2}}(Rcos(\theta)\hat{x}+Rsin(\theta)\hat{y}+z\hat{z})d\theta }[/math]
- Since both sine and cosine are [math]\displaystyle{ 2\pi }[/math] periodic functions, the [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] components of [math]\displaystyle{ \vec{E} }[/math] go to [math]\displaystyle{ \vec{0} }[/math], which is very convenient. The result is
- [math]\displaystyle{ \vec{E}=\frac{1}{4\pi\epsilon_{0}}\frac{Qz}{(z^{2}+R^{2})^{3/2}}\hat{z} }[/math].
Remark
If the path we are interested in is over a half circle, third-circle or quarter-circle, or indeed any circular section, simply adjust the bounds of integration and the charge density to the ones required by the curve of interest.
A Computational Model
This simulation shows the result of the computation for a ring composed of 2000 electrons. This is why the vector is pointing into the ring rather than out of the ring, which would happen for a ring composed of positively charged points.
Simplified Abstract Model
Added by GEORGE SORKIN, Spring 2024
Recall the equation we used to calculate and model the electric field caused by an electrically charged ring along the center of its axis:
- [math]\displaystyle{ \vec{E}=\frac{1}{4\pi\epsilon_{0}}\frac{Qz}{(z^{2}+R^{2})^{3/2}}\hat{z} }[/math].
This electric field model is dependent upon three variables: Q (electric charge), R (radius of the ring), and z (distance away from the center of the ring). This model is correct, i.e. it is completely accurate in all situations in the perfect world. We can create a more simplified model based on this model, given certain assumptions. This section will specifically explore how we can simplify this model when we assume that the distance from the ring is significantly larger than the radius of the ring (z >> R).
We can analyze this situation intuitively with an analogy. Imagine you are holding a ring directly in front of you, a couple of inches from your face. You would clearly see that the object is, in fact, ring-shaped. No surprise here. Now imagine that the ring is a mile away from your face. In this case, you may not even see the ring since it is so far away. And if you did, the shape would seem more like a point. You would not be able to identify the ring-shape property. This analogy is identical to our assumption of our simplified model; the ring's radius is so much significantly smaller than the distance. From the observer's point of view, it seems more like a point instead of a ring. This is fundamental to our simplified model. We will treat the ring as a point charge, an object with no radius.
We can analyze this situation logically and mathematically by exploring the extreme case: when the distance from the ring approaches infinity. Since the radius will remain finite, the scale between the distance and the radius also approaches infinity. As a result, the relative effect the radius will have on the model is essentially zero. Thus, we can completely discard the radius from our simplified model. As a result, we will only have two variables in our simplified model instead of three: Q (electric charge) and z (distance from the ring). We can derive this simplified model mathematically using limits.
- [math]\displaystyle{ \vec{E}=\lim_{R\to0}\left(\frac{1}{4\pi\epsilon_{0}}\frac{Qz}{(z^{2}+R^{2})^{3/2}}\hat{z}\right) =\frac{1}{4\pi\epsilon_{0}}\frac{Qz}{(z^{2}+\lim_{R\to0}\left(R\right)^{2})^{3/2}}\hat{z} =\frac{1}{4\pi\epsilon_{0}}\frac{Qz}{(z^{2})^{3/2}}\hat{z} =\frac{1}{4\pi\epsilon_{0}}\frac{Q}{z^{2}}\hat{z} }[/math]
This simplified model is identical to the equation for the electric field of a point charge. Based on this analysis, we can conclude that if the distance is significantly larger than the radius, we can treat the ring as a point charge. This interactive model demonstrates this concept perfectly. When our assumption holds, the percent error between this simplified model and the original model is extremely low.
Examples
Simple
1.) Find the function [math]\displaystyle{ E(x) }[/math] that represents the magnitude of the electric field along the center axis due to a uniformly charged ring of radius 0.04 m with total charge 8 C.
We can use the derived formula for the electric field due to a charged ring. Only the horizontal components of the electric field will remain as the rest will cancel out.
[math]\displaystyle{ E(x) = \frac{1}{4\pi\epsilon_{0}}\frac{(8 C)*x}{((0.04 m)^2 + x^2)^\frac{3}{2}} }[/math]
Middling
2.) A uniformly charged ring of radius 10.0 cm has a total charge of 91.0 µC. Find the electric field on the axis of the ring at the following distances from the center of the ring.
a. 1 cm
b. 5 cm
c. 30 cm
d. 100 cm
Use the derived formula, and convert the given distances into meters and the charge into Coulombs. Plug these into [math]\displaystyle{ x }[/math]
[math]\displaystyle{ E(x) = \frac{1}{4\pi\epsilon_{0}}\frac{Q*x}{(x^2 + R^2)^\frac{3}{2}} }[/math]
a. 8.069e6 N/C
b. 29.3e6 N/C
c. 7.76e6 N/C
d. 8.06e5 N/C
Difficult
Find the electric field at a distance [math]\displaystyle{ z }[/math] along the center axis away from a uniformly charged semicircular ring of radius R and total charge Q.
We can tweak the same integral for a uniformly charged ring by changing the limits of integration.
[math]\displaystyle{ \vec{E}=\int_{0}^{\pi}\frac{1}{4\pi\epsilon_{0}}\frac{q}{|\vec{r}|^{2}}\hat{r} d\theta=\int_{0}^{\pi}\frac{1}{4\pi\epsilon_{0}}\frac{Q}{\pi(R^{2}+z^{2})^{3/2}}(Rcos(\theta)\hat{x}+Rsin(\theta)\hat{y}+z\hat{z})d\theta }[/math]
[math]\displaystyle{ \vec{E} = \frac{1}{4\pi\epsilon_{0}}\frac{Q}{\pi(R^{2}+z^{2})^{3/2}}(0\hat{x}+2R\hat{y}+{\pi}z\hat{z}) }[/math]
Connectedness
Edited by AYESHA AHUJA Spring 2020
The idea of charge density is somewhat analogous to the idea of the mass density, which is useful in a variety of contexts, including the computation of the center of mass, the first and second moments of mass, which are useful in statics and rigid body dynamics. Instead of computing the uniform distribution of the mass of this ring, we are computing the uniform distribution of charge. This concept is also useful in visualizing what happens within a wire in a steady state circuit. The wire can be viewed to be a continuous length of rings of charge, which act as a channel through which electrons are transported, and that the electric field of these rings of charge pushes the electrons within the wire.
It is also important in the context of Maxwell's equations, specifically in Gauss's Law and in the Maxwell-Faraday equation, which are concerned with electron flux and induced fields, respectively.
History
Added by AYESHA AHUJA SPRING 2020
The first known time when charged rings were utilized to describe electromagnetism was during Faraday’s discovery of electrical induction. To conduct his experiments, Faraday used a ring made of iron that was attached to a battery. When this makeshift circuit was turned on it manipulated a compass needle by deflecting it. He showcased an induced current in the ring.
See also
Further reading
External links
References
- "Electric Field on the Axis of a Ring of Charge". University of Delaware Physics Library. Adapted from Stephen Kevan's lecture on Electric Fields and Charge Distribution. April 8, 1996. http://www.physics.udel.edu/~watson/phys208/exercises/kevan/efield1.html
- Chabay, R., & Sherwood, B. (2015). Matter and Interactions (4th ed., Vol. 2, pp. 597-599). Wiley.
- All images produced by the author