Biot-Savart Law: Difference between revisions
(Added vPython Link) |
|||
| (68 intermediate revisions by 7 users not shown) | |||
| Line 1: | Line 1: | ||
CLAIMED BY | CLAIMED BY Grant Reidy Fall 2024 | ||
[[File:Knight2_33.f.14.png|400px|thumb|right| | |||
CLAIMED BY Alexander Arredondo Fall 2023 | |||
CLAIMED BY Olivia Wang Fall 2023 | |||
[[File:Knight2_33.f.14.png|400px|thumb|right|Visualization of the magnetic fields generated around a current-carrying wire. [http://www4.uwsp.edu/physastr/kmenning/Phys250/Lect19.html]]]The Biot-Savart (pronounced bee-yo sahv-ar) Law quantitatively describes the magnetic field produced by a moving point charge. This law serves as the magnetic analog to Coulomb's Law, which describes electrical forces between static charges. [http://dev.physicslab.org/document.aspx?doctype=3&filename=magnetism_biotsavartlaw.xml] The law is named after Jean-Baptiste Biot and Felix Savart, the two scientists who discovered the law in 1820. | |||
==The Main Idea== | ==The Main Idea== | ||
A moving point produces a magnetic field in addition to the electric fields | A moving point charge produces a magnetic field in addition to its intrinsic electric field. Unlike the electric field that radiates outward symmetrically from a point charge, the magnetic field forms circular loops around the moving charge. | ||
The Biot-Savart Law relates magnetic fields to the currents which are their sources. In a similar manner, Coulomb's law relates electric fields to the point charges which are their sources. Finding the magnetic field resulting from a current distribution involves the vector product, and is inherently a calculus problem when the distance from the current to the field point is continuously changing. The Biot-Savart Law mathematically expresses the relationship between a current element and the resulting magnetic field it produces. | |||
The direction of the magnetic field contribution follows the right hand rule illustrated for a straight wire. This direction arises from the vector product nature of the dependence upon electric current. | |||
===A Mathematical Model=== | ===A Mathematical Model=== | ||
The | The single moving point charge form of the Biot-Savart Law is <math>\vec B=\frac{\mu_0}{4\pi}\frac{q\vec v \times \hat r}{r^2} </math>. The permeability of free space, or the ease of producing a magnetic field in a vacuum, is a constant <math> 4\pi \times 10^{-7} \frac{T * m^2}{C * \frac{m}{s}} </math>, denoted <math> \mu_0 </math>. The above equation describes the magnetic field vector <math> \vec B </math> at a point <math> \hat r </math> away from the moving point charge with velocity <math> \vec v </math> and charge <math> q </math>. '''Remember''' that <math> \vec r = \vec r_{obs} - \vec r_{source} </math> helps locate the observation point relative to the source of the magnetic field. '''Note:''' The charge <math> q </math> retains its sign in the Biot-Savart Law. For an electron, <math> q </math> in the Biot-Savart Law would be equal to <math> -1.6 \times 10^{-19} C </math>. | ||
The short wire form of the Biot-Savart Law is <math>\vec B=\frac{\mu_0}{4\pi}\frac{I \Delta\vec l \times \hat r}{r^2} </math>. This equation describes the magnetic field vector <math> \vec B </math> at a point <math> \hat r </math> away from the short wire with length <math> \Delta\vec l </math> and current <math> I </math>. | |||
'''Direction of the Magnetic Field Vector:''' | |||
The direction of the magnetic field vector is different from the direction of the electric field vector. The direction of the magnetic field vector is given by the cross product of two distinct vectors: namely either <math> \vec v </math> or <math> \Delta\vec l </math> and <math> \hat r </math>. The cross product of two vectors is perpendicular to the two original vectors. | |||
Example: Find the direction of the magnetic field of a point charge moving in the <math> +x </math> direction at a point in the <math> -y </math> direction. | |||
'''Magnitude of Magnetic Field:''' | Direction of <math> \vec B = \hat v \times \hat r = <1, 0, 0> \times <0, -1, 0> = \begin{bmatrix}\hat x & \hat y & \hat z \\ 1 & 0 & 0 \\ 0 & -1 & 0 \end{bmatrix} = <0, 0, -1> </math>, or in the <math> -z </math> direction | ||
The magnitude of the magnetic field is given by <math> | |||
You can also calculate the cross product, using formula <math> \vec A\times\vec B = < A_yB_z - A_zB_y, A_zB_x - A_xB_z, A_xB_y-A_yB_z> </math> | |||
'''Magnitude of Magnetic Field Vector:''' | |||
The magnitude of the magnetic field vector for a single moving point charge is given by <math> B = \frac{\mu_0}{4\pi} \frac{q v \sin\theta}{r^2} </math>, where <math> q v \sin\theta </math> is the polar form of the cross product and <math> \theta </math> is the angle between the two vectors <math> \vec v </math> and <math> \hat r </math>. Remember that this formula specifies spherical coordinates, where <math> \theta </math> is the angle between the velocity vector and the radial vector <math> \hat r </math>. | |||
The magnitude of the magnetic field vector for a short wire is given by <math> B = \frac{\mu_0}{4\pi} \frac{I \Delta l \sin\theta}{r^2} </math>, where <math> I \Delta l \sin\theta </math> is the polar form of the cross product and <math> \theta </math> is the angle between the two vectors <math> \Delta\vec l </math> and <math> \hat r </math>. | |||
===A Computational Model=== | ===A Computational Model=== | ||
Check out this link: https://trinket.io/glowscript/93785debae for a look at a moving point charge acted on by a magnetic force. This magnetic force acts on the point charge since the point charge is ''moving'' with a certain velocity. Magnetic force goes hand-in-hand with magnetic field. Just as a point charge can only create a magnetic field if the point charge is moving, a point charge can only feel the force from a magnetic field if the point charge has a velocity. This computational model shows how a moving point charge, which creates its own magnetic field, is acted on by an external magnetic field. | Check out this link: https://trinket.io/glowscript/93785debae for a look at a moving point charge acted on by a magnetic force. This magnetic force acts on the point charge since the point charge is ''moving'' with a certain velocity. Magnetic force goes hand-in-hand with magnetic field. Just as a point charge can only create a magnetic field if the point charge is moving, a point charge can only feel the force from a magnetic field if the point charge has a velocity. This computational model shows how a moving point charge, which creates its own magnetic field, is acted on by an external magnetic field. | ||
For a computational model of a wire carrying current, see the wiki page on the Biot-Savart Law for Currents | For a computational model of a wire carrying current, see the wiki page on the Biot-Savart Law for Currents [http://www.physicsbook.gatech.edu/Biot-Savart_Law_for_Currents]. | ||
===Using the Right-Hand Rule for Biot-Savart Law=== | |||
Put your index finger in the direction of the velocity of the particle, and your middle finger out towards the r hat. Make sure these two are 90 degrees away from each other. Now, stick your thumb up. If the particle you are following is positive, the cross product of the velocity of the particle and the r hat is in the direction of your thumb. If the particle is negative, the cross product of the particle and the r hat is in the opposite direction of your thumb. | |||
[[File:20190414 183245.jpg|center|300px]] | |||
===Solving Biot-Savart Problem strategy=== | |||
To solve Biot-Savart law problem, the following steps are helpful: | |||
1. Identify that the Biot-Savart law is the chosen method to solve the given problem. If there is symmetry in the problem comparing 𝐁⃗ and 𝐝𝐥⃗ ,Ampère’s law may be the preferred method to solve the question, which will be discussed in Ampère’s Law. | |||
2. Draw the current element length 𝑑𝐥⃗ and the unit vector 𝐫ˆ, noting that 𝑑𝐥⃗ points in the direction of the current and 𝐫ˆ points from the current element toward the point where the field is desired. | |||
3. Calculate the cross product 𝑑𝐥⃗ ×𝐫ˆ. The resultant vector gives the direction of the magnetic field according to the Biot-Savart law. | |||
4. Use Equation and substitute all given quantities into the expression to solve for the magnetic field. Note all variables that remain constant over the entire length of the wire may be factored out of the integration. | |||
5. Use the right-hand rule to verify the direction of the magnetic field produced from the current or to write down the direction of the magnetic field if only the magnitude was solved for in the previous part. | |||
==Examples== | ==Examples== | ||
| Line 30: | Line 64: | ||
===Example 1=== | ===Example 1=== | ||
An electron located at the origin is moving at <math> | An electron located at the origin is moving at <math> 2 \times 10^8 \frac{m}{s}</math> in the <math> +x </math> direction. What is the magnetic field at <math> <200, -300, 0> m </math> due to the moving electron? | ||
===Example 2=== | ===Example 2=== | ||
A proton is located on the +x axis and is moving with a velocity <math> \vec v </math> in the -y direction. What is the magnitude of the magnetic field due to the moving proton at <math> <0, 0, z> </math> if the angle <math> \theta </math> between <math> \vec v </math> of the proton and <math> \hat r </math> equals | A proton is located on the <math> +x </math> axis and is moving with a velocity <math> \vec v </math> in the <math> -y </math> direction. What is the magnitude of the magnetic field due to the moving proton at <math> <0, 0, z> </math> if the angle <math> \theta </math> between <math> \vec v </math> of the proton and <math> \hat r </math> equals <math> 34° </math>? | ||
===Example 3=== | ===Example 3=== | ||
An electron located at the origin is moving with velocity <math> \vec | An electron located at the origin is moving with velocity <math> \vec v_{electron} </math> in the <math> +z </math> direction. A proton is located directly in front of the electron and is moving with a velocity <math> \vec v_{proton} </math> in the <math> -y </math> direction. What is the magnetic field at the location of the proton due to the moving electron? | ||
===Example 4=== | |||
A thin plastic disk with radius <math> 500 cm </math> and negative charge <math> -6 \times 10^{-7} C </math> centered at the origin located in the <math> y-z </math> plane is rotating with a period of <math> 7 s </math> clockwise when viewed from the negative x axis. Determine the magnetic field at <math> \vec d = <-50000, 0, 0> cm. </math> | |||
===Answers | ===Answers=== | ||
'''Example 1:''' | '''Example 1:''' | ||
| Line 44: | Line 81: | ||
[[File:ex1.JPG|center|300px|Example 1]] | [[File:ex1.JPG|center|300px|Example 1]] | ||
First, calculate <math> \vec r </math>, which is <math> \vec r = <200, -300, 0>-<0,0,0>=<200, -300, 0> </math> | First, calculate <math> \vec r </math>, which is <math> \vec r = <200, -300, 0>-<0,0,0>=<200, -300, 0> m </math>. Using <math> \vec r </math>, calculate <math> \hat r </math>: | ||
<math> \hat r = \frac{ <200, -300, 0> }{\sqrt {200^2 + -300^2}}= <0.554, -0.832, 0> </math> | <math> \hat r = \frac{ <200, -300, 0> }{\sqrt {200^2 + -300^2}}= <0.554, -0.832, 0> </math> | ||
Next, calculate <math> q \vec v </math>. Remember that an electron carries a negative charge: <math> -1. | Next, calculate <math> q \vec v </math>. Remember that an electron carries a negative charge: <math> -1.6 \times 10^{-19}* <2 \times 10^8, 0, 0> = <-3.2 \times 10^{-11}, 0, 0> </math>. | ||
Next, compute the cross product, <math> q\vec v\times\hat r </math>. The cross product is given as <math> \vec A\times\vec B = < | Next, compute the cross product, <math> q\vec v\times\hat r </math>. The cross product is given as <math> \vec A\times\vec B = < A_xB_z - A_zB_y, A_zB_x - A_xB_z, A_xB_y-A_yB_z> </math> or by computing the determinant of the two vectors in a 3 x 3 matrix. The cross product in this case is <math> <0, 0, 2.65 \times 10^{-11}> </math>. | ||
Finally, divide <math> q\vec v\times\hat r </math> by the magnitude of <math> \vec r </math> squared: <math> \frac{ <0, 0, 2.65 \times 10^{-11}> }{360.55} = <0, 0, 7.34 \times 10^{-14}> </math>. Multiply by the constant <math> 1 \times 10^{-7} </math> given in the formula, and the final answer is <math> \vec B = <0, 0, 7.34 \times 10^{-21}> T </math> | |||
The determinant method effectively calculates the three-dimensional cross-product, which ensures the magnetic field vector is perpendicular to both original vectors. | |||
'''Example 2:''' | '''Example 2:''' | ||
| Line 59: | Line 98: | ||
We can then multiply the magnitudes of <math> q,\vec v, </math> and <math> sin </math> (<math>\theta </math>) to get the final answer: | We can then multiply the magnitudes of <math> q,\vec v, </math> and <math> sin </math> (<math>\theta </math>) to get the final answer: | ||
<math> B = \frac{\mu_0}{4\pi}\frac{qvsin( | <math> B = \frac{\mu_0}{4\pi}\frac{qvsin(34°)}{(\sqrt{x^2 + z^2})^2} </math> | ||
'''Example 3:''' | '''Example 3:''' | ||
| Line 65: | Line 104: | ||
[[File:ex3.JPG|center|300px|Example 3]] | [[File:ex3.JPG|center|300px|Example 3]] | ||
As seen in the diagram, <math> \hat r </math> from the proton to the electron is parallel to the electron's velocity. Therefore, <math> \vec | As seen in the diagram, <math> \hat r </math> from the proton to the electron is parallel to the electron's velocity. Therefore, <math> \vec v_{electron}\times\hat r </math> is zero because the two vectors are parallel (<math> \theta=0 </math>°). | ||
'''Example 4:''' | |||
[[File:Ex4.jpg|center|300px|Example 4]] | |||
To find the overall magnetic field vector at <math> \vec d </math>, the disk must be broken down into many infinitesimally small rings. | |||
Step 1: Find <math> dQ </math>, the amount of charge for an infinitesimal ring | |||
<math> \frac{dQ}{2\pi r dr} = \frac{Q}{\pi R^2} </math> | |||
<math> dQ = \frac{-6 \times 10^{-7}}{5^2\pi} 2\pi r dr = \frac{-12 \times 10^{-7}rdr}{25} </math> | |||
Step 2: Find <math> dI </math>, the current in this infinitesimal ring | |||
<math> dI = \frac{dQ}{T} = \frac {\frac{-12 \times 10^{-7}rdr}{25}}{7} = \frac{-12 \times 10^{-7}rdr}{175} </math> | |||
Step 3: Find <math> d\vec B </math>, the magnetic field vector for the infinitesimal ring | |||
<math> d\vec B = \frac {\mu_0}{4\pi} \frac {2 dI \pi R^2}{x^3} \hat x </math> | |||
<math> d\vec B (<-500, 0, 0>) = \frac {\mu_0}{4\pi} \frac {2 \frac{-12 \times 10^{-7}rdr}{175} \pi 5^2}{-500^3} \hat x = \frac{24 \times 10^{-14}rdr\pi}{7*500^3} \hat x </math> | |||
Step 4: Find <math> \vec B </math>, the magnetic field vector over the entire disk | |||
<math> \vec B = \int\limits_0^R\ d\vec B </math> | |||
<math> \vec B(<-500, 0, 0>) = \int\limits_0^5\ \frac{24 \times 10^{-14}rdr\pi}{7*500^3} \hat x = \frac {25}{2} \frac{24 \times 10^{-14} \pi}{7*500^3} T </math> | |||
==Applications== | ==Applications== | ||
===Sagged Conductors for Three Phase typical tower=== | |||
Application on Biot-Savart law for Sagged Conductors for Three Phase typical tower | |||
https://onlinelibrary.wiley.com/doi/10.1002/cae.20365 (2016) | |||
The Biot-Savart law is a fundamental principle in electromagnetism that describes the magnetic field produced by a steady current. It is commonly used to calculate the magnetic field around a current-carrying conductor. | |||
When applying the Biot-Savart law to sagged conductors in a three-phase transmission line on a typical tower, several factors need to be considered. Sagged conductors are often used in overhead transmission lines to accommodate thermal expansion and contraction as well as mechanical loads caused by wind. | |||
===Magnetic Response=== | ===Magnetic Response=== | ||
The Biot-Savart law has applications in nuclear magnetic resonance (NMR) spectroscopy, used to measure the chemical signals given off by compounds. The law can be used to calculate the magnetic responses at the atomic or molecular level, provided that the current density can be obtained mathematically. For more about NMR spectroscopy, see the wiki page [https://en.wikipedia.org/wiki/Nuclear_magnetic_resonance] [[File:Vortex.jpg|200px|thumb|right|In this example,[http://www.science20.com/news_articles/tendex_and_vortex_lines_new_way_visualize_warped_space_and_time-78171], the yellow arms represent whirring space from a black hole and the red lines represent vortex lines. Astrophysicists may use the Biot-Savart Law to calculate the velocity.]] | The Biot-Savart law has applications in nuclear magnetic resonance (NMR) spectroscopy, used to measure the chemical signals given off by compounds. The law can be used to calculate the magnetic responses at the atomic or molecular level, provided that the current density can be obtained mathematically. For more about NMR spectroscopy, see the wiki page [https://en.wikipedia.org/wiki/Nuclear_magnetic_resonance] [[File:Vortex.jpg|200px|thumb|right|In this example,[http://www.science20.com/news_articles/tendex_and_vortex_lines_new_way_visualize_warped_space_and_time-78171], the yellow arms represent whirring space from a black hole and the red lines represent vortex lines. Astrophysicists may use the Biot-Savart Law to calculate the velocity.]] | ||
===Aerodynamics=== | ===Aerodynamics=== | ||
In aerodynamics, the Biot-Savart law may be used to calculate the velocity induced by vortex lines, which are lines that are everywhere tangent to the vorticity vector. A vorticity vector is a pseudovector field that describes the tendency of something to rotate; in other words, the vorticity vector is the curl of the velocity field of a fluid. | In aerodynamics, the Biot-Savart law may be used to calculate the velocity induced by vortex lines, which are lines that are everywhere tangent to the vorticity vector. A vorticity vector is a pseudovector field that describes the tendency of something to rotate; in other words, the vorticity vector is the curl of the velocity field of a fluid. | ||
| Line 81: | Line 154: | ||
In 1819, Savart officially closed the doors of his medical practice and went to Paris to find a publisher for the translation of ''De medicina''. While there, he attended a lecture on acoustics by Jean-Baptiste Biot at the Faculty of Sciences. The two met there and began collaboration, when in 1820, Hans Christian Oersted published his findings regarding a compass needle's behavior when placed near a current-carrying wire: the needle pointed at right angles to the wire. Biot and Savart began looking more closely into the field produced by a current-carrying wire, and by using the oscillation of a magnetic dipole to determine the strength of the field close to a current-carrying wire, they discovered what is now called the Biot-Savart Law [[http://www-groups.dcs.st-and.ac.uk/~history/Biographies/Savart.html]]. | In 1819, Savart officially closed the doors of his medical practice and went to Paris to find a publisher for the translation of ''De medicina''. While there, he attended a lecture on acoustics by Jean-Baptiste Biot at the Faculty of Sciences. The two met there and began collaboration, when in 1820, Hans Christian Oersted published his findings regarding a compass needle's behavior when placed near a current-carrying wire: the needle pointed at right angles to the wire. Biot and Savart began looking more closely into the field produced by a current-carrying wire, and by using the oscillation of a magnetic dipole to determine the strength of the field close to a current-carrying wire, they discovered what is now called the Biot-Savart Law [[http://www-groups.dcs.st-and.ac.uk/~history/Biographies/Savart.html]]. | ||
== VPython Demo== | |||
[Interactive VPython Biot-Savart Demo](https://trinket.io/glowscript/877d2b5b77) | |||
== See also == | == See also == | ||
| Line 96: | Line 173: | ||
Matter & Interactions vol. II | Matter & Interactions vol. II | ||
Khawaja, Arsalan & Huang, Qi. (2016). Characteristic estimation of high voltage transmission line conductors with simultaneous magnetic field and current measurements. 1-6. 10.1109/I2MTC.2016.7520595. | |||
[[Category:Which Category did you place this in?]] | [[Category:Which Category did you place this in?]] | ||
Latest revision as of 18:47, 22 November 2024
CLAIMED BY Grant Reidy Fall 2024
CLAIMED BY Alexander Arredondo Fall 2023
CLAIMED BY Olivia Wang Fall 2023
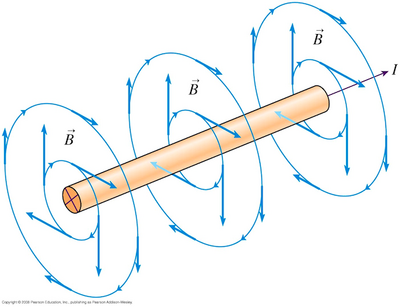
The Biot-Savart (pronounced bee-yo sahv-ar) Law quantitatively describes the magnetic field produced by a moving point charge. This law serves as the magnetic analog to Coulomb's Law, which describes electrical forces between static charges. [3] The law is named after Jean-Baptiste Biot and Felix Savart, the two scientists who discovered the law in 1820.
The Main Idea
A moving point charge produces a magnetic field in addition to its intrinsic electric field. Unlike the electric field that radiates outward symmetrically from a point charge, the magnetic field forms circular loops around the moving charge.
The Biot-Savart Law relates magnetic fields to the currents which are their sources. In a similar manner, Coulomb's law relates electric fields to the point charges which are their sources. Finding the magnetic field resulting from a current distribution involves the vector product, and is inherently a calculus problem when the distance from the current to the field point is continuously changing. The Biot-Savart Law mathematically expresses the relationship between a current element and the resulting magnetic field it produces.
The direction of the magnetic field contribution follows the right hand rule illustrated for a straight wire. This direction arises from the vector product nature of the dependence upon electric current.
A Mathematical Model
The single moving point charge form of the Biot-Savart Law is [math]\displaystyle{ \vec B=\frac{\mu_0}{4\pi}\frac{q\vec v \times \hat r}{r^2} }[/math]. The permeability of free space, or the ease of producing a magnetic field in a vacuum, is a constant [math]\displaystyle{ 4\pi \times 10^{-7} \frac{T * m^2}{C * \frac{m}{s}} }[/math], denoted [math]\displaystyle{ \mu_0 }[/math]. The above equation describes the magnetic field vector [math]\displaystyle{ \vec B }[/math] at a point [math]\displaystyle{ \hat r }[/math] away from the moving point charge with velocity [math]\displaystyle{ \vec v }[/math] and charge [math]\displaystyle{ q }[/math]. Remember that [math]\displaystyle{ \vec r = \vec r_{obs} - \vec r_{source} }[/math] helps locate the observation point relative to the source of the magnetic field. Note: The charge [math]\displaystyle{ q }[/math] retains its sign in the Biot-Savart Law. For an electron, [math]\displaystyle{ q }[/math] in the Biot-Savart Law would be equal to [math]\displaystyle{ -1.6 \times 10^{-19} C }[/math].
The short wire form of the Biot-Savart Law is [math]\displaystyle{ \vec B=\frac{\mu_0}{4\pi}\frac{I \Delta\vec l \times \hat r}{r^2} }[/math]. This equation describes the magnetic field vector [math]\displaystyle{ \vec B }[/math] at a point [math]\displaystyle{ \hat r }[/math] away from the short wire with length [math]\displaystyle{ \Delta\vec l }[/math] and current [math]\displaystyle{ I }[/math].
Direction of the Magnetic Field Vector:
The direction of the magnetic field vector is different from the direction of the electric field vector. The direction of the magnetic field vector is given by the cross product of two distinct vectors: namely either [math]\displaystyle{ \vec v }[/math] or [math]\displaystyle{ \Delta\vec l }[/math] and [math]\displaystyle{ \hat r }[/math]. The cross product of two vectors is perpendicular to the two original vectors.
Example: Find the direction of the magnetic field of a point charge moving in the [math]\displaystyle{ +x }[/math] direction at a point in the [math]\displaystyle{ -y }[/math] direction.
Direction of [math]\displaystyle{ \vec B = \hat v \times \hat r = \lt 1, 0, 0\gt \times \lt 0, -1, 0\gt = \begin{bmatrix}\hat x & \hat y & \hat z \\ 1 & 0 & 0 \\ 0 & -1 & 0 \end{bmatrix} = \lt 0, 0, -1\gt }[/math], or in the [math]\displaystyle{ -z }[/math] direction
You can also calculate the cross product, using formula [math]\displaystyle{ \vec A\times\vec B = \lt A_yB_z - A_zB_y, A_zB_x - A_xB_z, A_xB_y-A_yB_z\gt }[/math]
Magnitude of Magnetic Field Vector: The magnitude of the magnetic field vector for a single moving point charge is given by [math]\displaystyle{ B = \frac{\mu_0}{4\pi} \frac{q v \sin\theta}{r^2} }[/math], where [math]\displaystyle{ q v \sin\theta }[/math] is the polar form of the cross product and [math]\displaystyle{ \theta }[/math] is the angle between the two vectors [math]\displaystyle{ \vec v }[/math] and [math]\displaystyle{ \hat r }[/math]. Remember that this formula specifies spherical coordinates, where [math]\displaystyle{ \theta }[/math] is the angle between the velocity vector and the radial vector [math]\displaystyle{ \hat r }[/math].
The magnitude of the magnetic field vector for a short wire is given by [math]\displaystyle{ B = \frac{\mu_0}{4\pi} \frac{I \Delta l \sin\theta}{r^2} }[/math], where [math]\displaystyle{ I \Delta l \sin\theta }[/math] is the polar form of the cross product and [math]\displaystyle{ \theta }[/math] is the angle between the two vectors [math]\displaystyle{ \Delta\vec l }[/math] and [math]\displaystyle{ \hat r }[/math].
A Computational Model
Check out this link: https://trinket.io/glowscript/93785debae for a look at a moving point charge acted on by a magnetic force. This magnetic force acts on the point charge since the point charge is moving with a certain velocity. Magnetic force goes hand-in-hand with magnetic field. Just as a point charge can only create a magnetic field if the point charge is moving, a point charge can only feel the force from a magnetic field if the point charge has a velocity. This computational model shows how a moving point charge, which creates its own magnetic field, is acted on by an external magnetic field.
For a computational model of a wire carrying current, see the wiki page on the Biot-Savart Law for Currents [4].
Using the Right-Hand Rule for Biot-Savart Law
Put your index finger in the direction of the velocity of the particle, and your middle finger out towards the r hat. Make sure these two are 90 degrees away from each other. Now, stick your thumb up. If the particle you are following is positive, the cross product of the velocity of the particle and the r hat is in the direction of your thumb. If the particle is negative, the cross product of the particle and the r hat is in the opposite direction of your thumb.
Solving Biot-Savart Problem strategy
To solve Biot-Savart law problem, the following steps are helpful:
1. Identify that the Biot-Savart law is the chosen method to solve the given problem. If there is symmetry in the problem comparing 𝐁⃗ and 𝐝𝐥⃗ ,Ampère’s law may be the preferred method to solve the question, which will be discussed in Ampère’s Law.
2. Draw the current element length 𝑑𝐥⃗ and the unit vector 𝐫ˆ, noting that 𝑑𝐥⃗ points in the direction of the current and 𝐫ˆ points from the current element toward the point where the field is desired.
3. Calculate the cross product 𝑑𝐥⃗ ×𝐫ˆ. The resultant vector gives the direction of the magnetic field according to the Biot-Savart law.
4. Use Equation and substitute all given quantities into the expression to solve for the magnetic field. Note all variables that remain constant over the entire length of the wire may be factored out of the integration.
5. Use the right-hand rule to verify the direction of the magnetic field produced from the current or to write down the direction of the magnetic field if only the magnitude was solved for in the previous part.
Examples
See below for solutions to these examples.
Example 1
An electron located at the origin is moving at [math]\displaystyle{ 2 \times 10^8 \frac{m}{s} }[/math] in the [math]\displaystyle{ +x }[/math] direction. What is the magnetic field at [math]\displaystyle{ \lt 200, -300, 0\gt m }[/math] due to the moving electron?
Example 2
A proton is located on the [math]\displaystyle{ +x }[/math] axis and is moving with a velocity [math]\displaystyle{ \vec v }[/math] in the [math]\displaystyle{ -y }[/math] direction. What is the magnitude of the magnetic field due to the moving proton at [math]\displaystyle{ \lt 0, 0, z\gt }[/math] if the angle [math]\displaystyle{ \theta }[/math] between [math]\displaystyle{ \vec v }[/math] of the proton and [math]\displaystyle{ \hat r }[/math] equals [math]\displaystyle{ 34° }[/math]?
Example 3
An electron located at the origin is moving with velocity [math]\displaystyle{ \vec v_{electron} }[/math] in the [math]\displaystyle{ +z }[/math] direction. A proton is located directly in front of the electron and is moving with a velocity [math]\displaystyle{ \vec v_{proton} }[/math] in the [math]\displaystyle{ -y }[/math] direction. What is the magnetic field at the location of the proton due to the moving electron?
Example 4
A thin plastic disk with radius [math]\displaystyle{ 500 cm }[/math] and negative charge [math]\displaystyle{ -6 \times 10^{-7} C }[/math] centered at the origin located in the [math]\displaystyle{ y-z }[/math] plane is rotating with a period of [math]\displaystyle{ 7 s }[/math] clockwise when viewed from the negative x axis. Determine the magnetic field at [math]\displaystyle{ \vec d = \lt -50000, 0, 0\gt cm. }[/math]
Answers
Example 1:

First, calculate [math]\displaystyle{ \vec r }[/math], which is [math]\displaystyle{ \vec r = \lt 200, -300, 0\gt -\lt 0,0,0\gt =\lt 200, -300, 0\gt m }[/math]. Using [math]\displaystyle{ \vec r }[/math], calculate [math]\displaystyle{ \hat r }[/math]: [math]\displaystyle{ \hat r = \frac{ \lt 200, -300, 0\gt }{\sqrt {200^2 + -300^2}}= \lt 0.554, -0.832, 0\gt }[/math]
Next, calculate [math]\displaystyle{ q \vec v }[/math]. Remember that an electron carries a negative charge: [math]\displaystyle{ -1.6 \times 10^{-19}* \lt 2 \times 10^8, 0, 0\gt = \lt -3.2 \times 10^{-11}, 0, 0\gt }[/math]. Next, compute the cross product, [math]\displaystyle{ q\vec v\times\hat r }[/math]. The cross product is given as [math]\displaystyle{ \vec A\times\vec B = \lt A_xB_z - A_zB_y, A_zB_x - A_xB_z, A_xB_y-A_yB_z\gt }[/math] or by computing the determinant of the two vectors in a 3 x 3 matrix. The cross product in this case is [math]\displaystyle{ \lt 0, 0, 2.65 \times 10^{-11}\gt }[/math].
Finally, divide [math]\displaystyle{ q\vec v\times\hat r }[/math] by the magnitude of [math]\displaystyle{ \vec r }[/math] squared: [math]\displaystyle{ \frac{ \lt 0, 0, 2.65 \times 10^{-11}\gt }{360.55} = \lt 0, 0, 7.34 \times 10^{-14}\gt }[/math]. Multiply by the constant [math]\displaystyle{ 1 \times 10^{-7} }[/math] given in the formula, and the final answer is [math]\displaystyle{ \vec B = \lt 0, 0, 7.34 \times 10^{-21}\gt T }[/math]
The determinant method effectively calculates the three-dimensional cross-product, which ensures the magnetic field vector is perpendicular to both original vectors.
Example 2:

First, as in example one, calculate [math]\displaystyle{ \vec r }[/math], and then the magnitude of [math]\displaystyle{ \vec r }[/math]. [math]\displaystyle{ \vec r = \lt 0, 0, z\gt - \lt x, 0, 0\gt = \lt -x, 0, z\gt }[/math]. The magnitude of [math]\displaystyle{ \vec r }[/math] is then [math]\displaystyle{ \sqrt{x^2 + z^2} }[/math]. We can then multiply the magnitudes of [math]\displaystyle{ q,\vec v, }[/math] and [math]\displaystyle{ sin }[/math] ([math]\displaystyle{ \theta }[/math]) to get the final answer:
[math]\displaystyle{ B = \frac{\mu_0}{4\pi}\frac{qvsin(34°)}{(\sqrt{x^2 + z^2})^2} }[/math]
Example 3:

As seen in the diagram, [math]\displaystyle{ \hat r }[/math] from the proton to the electron is parallel to the electron's velocity. Therefore, [math]\displaystyle{ \vec v_{electron}\times\hat r }[/math] is zero because the two vectors are parallel ([math]\displaystyle{ \theta=0 }[/math]°).
Example 4:
To find the overall magnetic field vector at [math]\displaystyle{ \vec d }[/math], the disk must be broken down into many infinitesimally small rings.
Step 1: Find [math]\displaystyle{ dQ }[/math], the amount of charge for an infinitesimal ring
[math]\displaystyle{ \frac{dQ}{2\pi r dr} = \frac{Q}{\pi R^2} }[/math]
[math]\displaystyle{ dQ = \frac{-6 \times 10^{-7}}{5^2\pi} 2\pi r dr = \frac{-12 \times 10^{-7}rdr}{25} }[/math]
Step 2: Find [math]\displaystyle{ dI }[/math], the current in this infinitesimal ring
[math]\displaystyle{ dI = \frac{dQ}{T} = \frac {\frac{-12 \times 10^{-7}rdr}{25}}{7} = \frac{-12 \times 10^{-7}rdr}{175} }[/math]
Step 3: Find [math]\displaystyle{ d\vec B }[/math], the magnetic field vector for the infinitesimal ring
[math]\displaystyle{ d\vec B = \frac {\mu_0}{4\pi} \frac {2 dI \pi R^2}{x^3} \hat x }[/math]
[math]\displaystyle{ d\vec B (\lt -500, 0, 0\gt ) = \frac {\mu_0}{4\pi} \frac {2 \frac{-12 \times 10^{-7}rdr}{175} \pi 5^2}{-500^3} \hat x = \frac{24 \times 10^{-14}rdr\pi}{7*500^3} \hat x }[/math]
Step 4: Find [math]\displaystyle{ \vec B }[/math], the magnetic field vector over the entire disk
[math]\displaystyle{ \vec B = \int\limits_0^R\ d\vec B }[/math]
[math]\displaystyle{ \vec B(\lt -500, 0, 0\gt ) = \int\limits_0^5\ \frac{24 \times 10^{-14}rdr\pi}{7*500^3} \hat x = \frac {25}{2} \frac{24 \times 10^{-14} \pi}{7*500^3} T }[/math]
Applications
Sagged Conductors for Three Phase typical tower
Application on Biot-Savart law for Sagged Conductors for Three Phase typical tower https://onlinelibrary.wiley.com/doi/10.1002/cae.20365 (2016) The Biot-Savart law is a fundamental principle in electromagnetism that describes the magnetic field produced by a steady current. It is commonly used to calculate the magnetic field around a current-carrying conductor. When applying the Biot-Savart law to sagged conductors in a three-phase transmission line on a typical tower, several factors need to be considered. Sagged conductors are often used in overhead transmission lines to accommodate thermal expansion and contraction as well as mechanical loads caused by wind.
Magnetic Response
The Biot-Savart law has applications in nuclear magnetic resonance (NMR) spectroscopy, used to measure the chemical signals given off by compounds. The law can be used to calculate the magnetic responses at the atomic or molecular level, provided that the current density can be obtained mathematically. For more about NMR spectroscopy, see the wiki page [5]

Aerodynamics
In aerodynamics, the Biot-Savart law may be used to calculate the velocity induced by vortex lines, which are lines that are everywhere tangent to the vorticity vector. A vorticity vector is a pseudovector field that describes the tendency of something to rotate; in other words, the vorticity vector is the curl of the velocity field of a fluid.
Medical Technology
Aside from applications in aerospace engineering and chemistry, the Biot-Savart law also plays an important role in magnetic resonance imaging (MRI). MRIs are a crucial piece of technology in the medical field; they are used for diagnosing cancer, detecting stress fractures, analyzing musculoskeletal injuries, and much more. An MRI machine is essentially one large magnetic field, and the hydrogen proton's axes in the human body all line up when a person is placed in an MRI. The magnetic field in an MRI is created by electric coils with moving electrons, which carry a current through the coils. This current is produced by exposing moving electrons to the electric field in the coils. if the moving electrons did not create magnetic fields, then no current would run through the coils, and MRIs would not exist.
History
Felix Savart was born on June 30, 1791 in Mezieres, France to a family with a strong association with military engineering schools. While completing his formal education in 1808 at the university in Metz, Savart decided to pursue medicine and become a physician. After serving a short stint in Napoleon's army in the the first engineering battalion, he resumed his medical training and graduated from Strasbourg in 1816. During his medical studies, Savart became interested in first century Roman writer Aulus Cornelius Celsus and his famous medical book De medicinia. Savart began working on a translation and set up a medical practice in Metz in 1817, but he gradually became more interested in physics rather than patients, particularly in sound and acoustics. He began building violins as a way to explore the form of the instrument through mathematical principles.
In 1819, Savart officially closed the doors of his medical practice and went to Paris to find a publisher for the translation of De medicina. While there, he attended a lecture on acoustics by Jean-Baptiste Biot at the Faculty of Sciences. The two met there and began collaboration, when in 1820, Hans Christian Oersted published his findings regarding a compass needle's behavior when placed near a current-carrying wire: the needle pointed at right angles to the wire. Biot and Savart began looking more closely into the field produced by a current-carrying wire, and by using the oscillation of a magnetic dipole to determine the strength of the field close to a current-carrying wire, they discovered what is now called the Biot-Savart Law [[6]].
VPython Demo
[Interactive VPython Biot-Savart Demo](https://trinket.io/glowscript/877d2b5b77)
See also
Right hand rule [[7]] Biot-Savart Law for Currents [[8]] Jean-Baptiste Biot [[9]].
External links
"Teach Engineering" on Biot-Savart [10] Derivation and Examples [11] Biot-Savart and Ampere's Law on MIT OpenCourse [12]
References
Matter & Interactions vol. II
Khawaja, Arsalan & Huang, Qi. (2016). Characteristic estimation of high voltage transmission line conductors with simultaneous magnetic field and current measurements. 1-6. 10.1109/I2MTC.2016.7520595.