Gauss's Law: Difference between revisions
No edit summary |
No edit summary |
||
| (55 intermediate revisions by 9 users not shown) | |||
| Line 1: | Line 1: | ||
'''Claimed by | '''Claimed by James Swope (Fall 2020), Edited by Nabiha Ahsan (Fall 2021), Edited by Tyler Morgan(Fall 2023), Edited by Anshu Dendukuri(Spring 2024)''' | ||
<!--I apologize for my apparent lack of contribution. I had hoped to create a great deal of new content (specifically a computational model and a few hard examples), however, I ended up running out of time. I was also unable to finish tidying up/rewriting the article. Please don't judge me too critically. | |||
TO DO: | |||
Re-write for consistent tone/style | |||
Provide more examples (easy/hard) | |||
Add diagrams | |||
Add brief descriptions to each external link/source | |||
Create computational model--> | |||
Gauss's Law is | |||
Gauss's Law is a very powerful law that spans a diverse array of fields, with applications in physics, mathematics, chemistry, and engineering, among others. Along with [[James Maxwell]]'s other three equations, Gauss's Law forms the foundation of classical electrodynamics. | |||
==The Main Idea== | |||
[[File:Gaussian Box Ex.jpg|thumb|Three-dimensional Gaussian surface]] | |||
Picture a three-dimensional solid object in space that does not have any charges around it. Suppose that you discover an electric field is directed radially outward from all faces of the object. You then measure the magnitude of the electric field at each face. Without being able to open the object and determine its charge distribution, how might you determine the charge inside the object? | |||
This simple situation illustrates one basic application of Gauss's Law: Using the measured electric field flowing through the faces of a closed surface to determine the charge that lies inside. | |||
===A Mathematical Model=== | |||
Gauss's Law elegantly relates the net charge enclosed within a ''Gaussian surface'' to the patterns of electric field that flow over its faces ([[Electric Flux]]). A Gaussian surface is any surface belonging to a closed three-dimensional object. <!--Include picture of examples of surfaces that ARE Gaussian surfaces and surfaces that are NOT Gaussian surfaces--> | |||
In words, the law states that the net electric flux outside a surface is equal to the ratio of the total enclosed charge inside the surface to the permittivity of free space. Symbolically, this is written as the area integral | |||
<math>\oint \vec E \cdot \hat{n} ~dA = \frac{\sum Q_{inside}}{\varepsilon_{0}}</math> | |||
where <math> \vec E </math> is the net electric field acting through the surface, <math> \hat{n}</math> is the unit normal vector perpendicular to the face of the surface, and <math> dA </math> is the surface area of the face being examined. | |||
<!--"Returning to the example mentioned above, [provide a worked example calculating the charge inside the box, given values of E and the dimensions of the box]"--> | |||
From the definition of [[Electric Flux]], Gauss's Law may also be written equivalently as | |||
<math> \Phi_{el} = \frac{Q_{enclosed}}{\varepsilon_{0}}</math> | |||
====Relation to Coulomb's Law==== | |||
Additionally, Coulomb's Law and Gauss's Law are innately connected. Coulomb's Law relates charge to electric field. Gauss's Law relates charge to electric flux. Both laws, relate charge to an electrical property. For clarification, the electric flux is a quantity that is equal to the product of the perpendicular component of E-field and the area of the closed surface. Not only do these two laws look similar at the surface, but using one law it is quite easy to derive the other law. | Additionally, Coulomb's Law and Gauss's Law are innately connected. Coulomb's Law relates charge to electric field. Gauss's Law relates charge to electric flux. Both laws, relate charge to an electrical property. For clarification, the electric flux is a quantity that is equal to the product of the perpendicular component of E-field and the area of the closed surface. Not only do these two laws look similar at the surface, but using one law it is quite easy to derive the other law. | ||
====Relationship Between Charge and Flux==== | |||
== | |||
We know from the previous introduction of flux that there is a relationship between the electric flux on a closed surface and the charges inside the surface. However, we would like to figure out what that particular factor is. | We know from the previous introduction of flux that there is a relationship between the electric flux on a closed surface and the charges inside the surface. However, we would like to figure out what that particular factor is. | ||
We start by considering a point charge of +Q enclosed by an imaginary spherical shell. | We start by considering a point charge of <math>+Q</math> enclosed by an imaginary spherical shell. | ||
[[File:gaussv2212.jpg]] | [[File:gaussv2212.jpg]] | ||
Everywhere on the imaginary shell, the electric field produced is parallel to the normal unit vector. Cos(0) = 1, so the dot product | Everywhere on the imaginary shell, the electric field produced is parallel to the normal unit vector. Cos(0) = 1, so the dot product is simply the magnitude of the electric field. Recall that the surface area of the imaginary sphere is <math>4 \pi r^{2}</math>. With Coulomb's Law and the surface area of a sphere, we get that electric flux is equal to <math>\frac{+Q}{\varepsilon_{0}}</math>. This implies that the factor is <math>\frac{1}{\varepsilon_{0}}</math>. | ||
Note that if the point charge was negative, the electric field would still be parallel, just opposite direction. Cos(180) = -1 so the dot product would be -1 times the magnitude of the electric field. | Note that if the point charge was negative, the electric field would still be parallel, just opposite direction. Cos(180) = -1 so the dot product would be -1 times the magnitude of the electric field. | ||
To understand this law more fully, one can look at the diagram below. As can be seen on the left side of this diagram, change in flux equals electric field multiplied by change in area. This is the basis for the equation ф=∮E da. When you integrate the change of A, you get the flux. | |||
Image Taken from Hyperphysics | Image Taken from Hyperphysics | ||
| Line 32: | Line 58: | ||
To more clearly state it, in integral form, the formula for this Law is the electric flux equals the total charge contained by a closed surface, divided by the permittivity ( | To more clearly state it, in integral form, the formula for this Law is the electric flux equals the total charge contained by a closed surface, divided by the permittivity (<math>\varepsilon_{0} = 8.854187817...×10^{-12} ~F*m^{-1}</math>). | ||
[[File:Adc2dff3156800a39ef0a9df76a7d868.png]] | [[File:Adc2dff3156800a39ef0a9df76a7d868.png]] | ||
| Line 41: | Line 67: | ||
[[File:Screen Shot 2018-04-18 at 5.31.54 PM.png]] | [[File:Screen Shot 2018-04-18 at 5.31.54 PM.png]] | ||
In this equation, ρ is electric charge density, ∇*E is divergence of electric field, and | In this equation, ρ is electric charge density, ∇*E is divergence of electric field, and <math>\varepsilon_{0} = 8.854187817...×10^{-12} ~F*m^{-1}</math>. | ||
Below is a brief summary of what has been covered. | |||
[[File:Gauss_14.jpg]] | |||
==A Computational Model== | |||
An extremely rudimentary explanation of Gauss's Law is: https://www.youtube.com/watch?v=f2Cccp6XBUY | |||
To visualization of Gauss's law with computational model: https://www.youtube.com/watch?v=i5N36mWsdGo | |||
Experimental demonstration of Gauss's law: https://www.youtube.com/watch?v=r3w4FAUOLuM | |||
Visual explaination of Gauss Divergence Theorem(Khan Academy): https://www.youtube.com/watch?v=XyiQ2dwJHXE | |||
To view the applications of Gauss's law in a coding setting (Python GLowScript): https://trinket.io/glowscript/f618920f61 | |||
==Examples== | ==Examples== | ||
===Easy Examples=== | |||
====Easy Example 1==== | |||
Looking at the images on the right hand side of the screen, we find an easy example in which we will find the electric field in a uniformly charged plate (+Q). | Looking at the images on the right hand side of the screen, we find an easy example in which we will find the electric field in a uniformly charged plate (+Q). | ||
Recall Gauss's Formula: | 1. Recall Gauss's Formula: | ||
[[File:Gauss for.jpg| | [[File:Gauss for.jpg|400px]] | ||
2. Now look carefully at the diagram below and go through each of the surfaces one by one. Ask yourself, in what direction does the normal vector point? | 2. Now look carefully at the diagram below and go through each of the surfaces one by one. Ask yourself, in what direction does the normal vector point? | ||
[[File:Gauss ex.jpg|400px | [[File:Gauss ex.jpg|400px]] | ||
3. Therefore, in the sides where there is 90 degree angle made with E, the flux will just be zero! | 3. Therefore, in the sides where there is 90 degree angle made with E, the flux will just be zero! | ||
[[File:Gauss fl.jpg| | [[File:Gauss fl.jpg|400px]] | ||
4. In the only case where the flux is not zero is in the sides A and B of the box (which are the same in magnitude). We compute the flux as follows: | 4. In the only case where the flux is not zero is in the sides A and B of the box (which are the same in magnitude). We compute the flux as follows: | ||
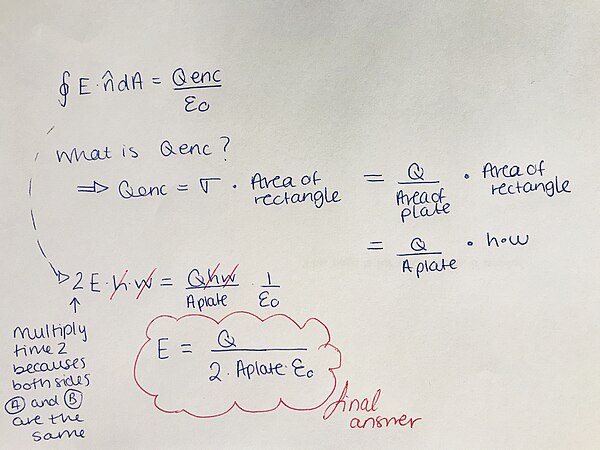
[[File:Gauss ans.jpg| | [[File:Gauss ans.jpg|600px]] | ||
Remember, when doing Gauss's problems, always think about you n vector before diving into the formula. | Remember, when doing Gauss's problems, always think about you n vector before diving into the formula. | ||
====Easy Example 2==== | |||
Consider a point charge <math> Q = +2 \, \text{μC} </math> enclosed by a spherical Gaussian surface with a radius of <math> r = 10 \, \text{cm} </math>. Calculate the electric flux through the surface. | |||
**Solution:** | |||
Using Gauss's Law, the electric flux <math>( \Phi_{el} )</math> through a closed surface is given by <math> \Phi_{el} = \frac{Q_{enclosed}}{\varepsilon_{0}} </math>. For a point charge enclosed by a spherical surface, the electric flux is simply <math> \frac{Q}{\varepsilon_{0}} </math>. Substituting the given values: | |||
<math> \Phi_{el} = \frac{2 \times 10^{-6} \, \text{C}}{8.854 \times 10^{-12} \, \text{C}^2/\text{N}\cdot\text{m}^2} </math> | |||
===Intermediate Examples=== | |||
====Example 1==== | |||
The example below shows how to determine the net charge located inside a box and is fundamental to understanding Gauss's Law. It demonstrates the idea that to calculate the net charge inside a box, we have to start off by calculating the fluxes acting on all surfaces on the box by using the Gauss's Law. | |||
[[File:Wiki resource.jpg|600px]] | |||
====Example 2==== | |||
The example below shows how to calculate the net charge enclosed by a box. | |||
[[File:Wiki resource2.jpg|600px]] | |||
Example 3 | ====Example 3==== | ||
In order to apply Gauss's Law, it is important to be certain you are working with a closed surface, then set electric flux equal to the internal field divided by the permittivity (<math>\varepsilon_{0} = 8.854187817...×10^{-12} ~F*m^{-1}</math>). An example of this Law being applied can be found below. | |||
[[File: | [[File:Gauss_law3.png|600px]] | ||
====Example 4==== | |||
In this example, the Qenc is equal to zero. This was determined by adding up all of the fluxes through every surface. This can also be determined by seeing that the same fluxes travel through the same areas of the tent. The equation Ф=∮B da=0 helps explain this when considering that Ф is the same in both equations. | |||
[[File:Gauss's_Law1234.jpeg|600px]] | |||
===Hard Examples=== | |||
====Example 1==== | |||
Inside a non-uniformly charged sphere with a volume charge density <math>\rho(r) = \rho_0 r^2 </math> for <math>0 \leq r \leq R </math>, where <math>\rho_0</math> is a constant and R is the radius of the sphere. Find the electric field at a distance r from the center, where r is between 0 and R, using Gauss's Law. | |||
=====Solution:===== | |||
To find the electric field inside the sphere, create a Gaussian surface and take advantage of the spherical symmetry. The charge enclosed within a Gaussian sphere of radius <math>r</math> is <math>\frac{4}{3}\pi \rho_0 r^3 </math>. Gauss's Law then gives <math>E = \frac{\rho_0 r}{3\varepsilon_0} </math>. | |||
====Example 2==== | |||
A long, straight wire carries a non-uniform linear charge density <math> \lambda(z) = \lambda_0 e^{-az} </math>, where <math>\lambda_0</math> and a are constants, and z is the distance along the wire. Determine the electric field at a distance r from the wire using Gauss's Law. | |||
=====Solution:===== | |||
Set up a Gaussian cylindrical surface around the wire to take advantage of the cylindrical symmetry. The total charge enclosed within the Gaussian surface is found by integrating the linear charge density along the length of the cylinder. Gauss's Law then gives <math>E = \frac{\lambda_0}{2\pi\varepsilon_0 r} \int_{-\infty}^{\infty} e^{-az} \, dz </math>. Solving this integral yields the expression for the electric field as a function of r. | |||
==Connectedness== | ==Connectedness== | ||
Gauss's Law, | Gauss's Law can be found in many areas of science, technology, engineering, and mathematics. In fact, Gauss's Law and other Maxwell Equations form a basis for electrodynamics. They are the fundamental core of this field of study. Gauss's Law is also connected to the Gaussian/Normal distribution, which is a continuous probability distribution that is characterized by a bell-shaped curve. This distribution is found throughout statistics and probability and is used everyday by people in STEM fields. | ||
As Industrial and Systems Engineering majors, we deal with many statistical distributions. A very important fundamental distribution is the Gaussian distribution or the Normal Distribution. With inference, the Gaussian Distribution comes up in confidence intervals for single statistics. With comparison inference, like finding the pairwise difference between statistics, generally we use other distributions such as the T-Distribution. However, the T-Distribution approximates the Gaussian distribution with degrees of freedom greater than 29. | As Industrial and Systems Engineering majors, we deal with many statistical distributions. A very important fundamental distribution is the Gaussian distribution or the Normal Distribution. With inference, the Gaussian Distribution comes up in confidence intervals for single statistics. With comparison inference, like finding the pairwise difference between statistics, generally we use other distributions such as the T-Distribution. However, the T-Distribution approximates the Gaussian distribution with degrees of freedom greater than 29. | ||
As civil and environmental engineering majors, we also deal with the Gaussian/Normal Distribution in our fields. As an example, the speed data of traffic on a highway is said to follow the normal distribution. | As civil and environmental engineering majors, we also deal with the Gaussian/Normal Distribution in our fields. As an example, the speed data of traffic on a highway is said to follow the normal distribution. | ||
Additional to many engineering majors. Gauss's Law has applications in many different STEM job fields. Engineering majors learn about the different Gaussian laws in college and apply them in there jobs. Millions of people are applying his laws to the world and will continue to do so. Gauss has had a huge impact on the world and will continue to have a big impact on the future. Gauss has done great work with his work. | |||
==History== | ==History== | ||
[[File:220px-Carl_Friedrich_Gauss_(C._A._Jensen).jpg]] | [[File:220px-Carl_Friedrich_Gauss_(C._A._Jensen).jpg||Portrait of Gauss]] | ||
Gauss's Law was first 'discovered' in 1773, by the great mathematician Joseph-Louis Lagrange. It was further developed by Carl Friedrich Gauss in 1813. The law was inspired by Coulomb's law. | |||
Gauss was a prolific German mathematician and physicist. He made significant contributions to a variety of fields in mathematics and physics. In fact his contributions are so great that he is referred to as the "greatest mathematician since antiquity" and the "foremost of mathematicians". | |||
Gauss is also known for his advancements in the astronomy field. While the dwarf planet Ceres was discovered by Giuseppe Piazza (Italian astronomer), Gauss was able to predict the position for its rediscovery. Due to the methodology behind this rediscovery, Gauss's Method, there was also significant advancements in the theory of the motion of planetoids, which introduced the Gaussian gravitation constant. | |||
The foundation for Gauss's law was laid by Isaac Newton, who formulated the inverse-square law of gravitation in 1687. This idea of forces diminishing with the square of distance inspired analogous formulations for electrostatics. In 1785, Charles-Augustin de Coulomb experimentally confirmed that electric forces between charges follow an inverse-square law. The concept of a field—an invisible influence extending through space—began to take shape in the late 18th and early 19th centuries. | |||
Mathematicians and physicists, including Joseph Priestley and others, laid groundwork for understanding how charges influence surrounding regions. Gauss formulated the law in his personal notes in 1835. These notes contained his ideas on how electric fields could be mathematically related to charges through surface integrals. His reluctance to publish might have been due to the lack of experimental confirmation at the time or his tendency to prioritize mathematical rigor over immediate dissemination. The law became widely known as part of James Clerk Maxwell’s unification of electromagnetic theory in the 1860s. Maxwell included Gauss’s law as one of his four foundational equations in Maxwell’s Equations. Although Maxwell credited earlier physicists, including Gauss, Faraday, and Ampère, the incorporation of Gauss’s law into a cohesive electromagnetic theory marked its formal introduction into mainstream physics. By the late 19th century, Gauss’s law was being taught in academic settings as a fundamental part of electrostatics and electromagnetism. It gained recognition in its integral and differential forms, largely through Maxwell’s equations and the broader development of vector calculus. | |||
== See also == | == See also == | ||
===Further Reading=== | |||
Gauss's Law is tied in closely with the other of Maxwell's equations that can be found here in the Physics Book. | Gauss's Law is tied in closely with the other of Maxwell's equations that can be found here in the Physics Book. | ||
| Line 143: | Line 221: | ||
[[Category: | [[Category: Electric Field]] | ||
[[Category: Fields]] | |||
[[Category: Gauss's Law]] | |||
[[Category: Maxwell's Equations]] | |||
Latest revision as of 16:42, 23 November 2024
Claimed by James Swope (Fall 2020), Edited by Nabiha Ahsan (Fall 2021), Edited by Tyler Morgan(Fall 2023), Edited by Anshu Dendukuri(Spring 2024)
Gauss's Law is a very powerful law that spans a diverse array of fields, with applications in physics, mathematics, chemistry, and engineering, among others. Along with James Maxwell's other three equations, Gauss's Law forms the foundation of classical electrodynamics.
The Main Idea
Picture a three-dimensional solid object in space that does not have any charges around it. Suppose that you discover an electric field is directed radially outward from all faces of the object. You then measure the magnitude of the electric field at each face. Without being able to open the object and determine its charge distribution, how might you determine the charge inside the object?
This simple situation illustrates one basic application of Gauss's Law: Using the measured electric field flowing through the faces of a closed surface to determine the charge that lies inside.
A Mathematical Model
Gauss's Law elegantly relates the net charge enclosed within a Gaussian surface to the patterns of electric field that flow over its faces (Electric Flux). A Gaussian surface is any surface belonging to a closed three-dimensional object. In words, the law states that the net electric flux outside a surface is equal to the ratio of the total enclosed charge inside the surface to the permittivity of free space. Symbolically, this is written as the area integral
[math]\displaystyle{ \oint \vec E \cdot \hat{n} ~dA = \frac{\sum Q_{inside}}{\varepsilon_{0}} }[/math]
where [math]\displaystyle{ \vec E }[/math] is the net electric field acting through the surface, [math]\displaystyle{ \hat{n} }[/math] is the unit normal vector perpendicular to the face of the surface, and [math]\displaystyle{ dA }[/math] is the surface area of the face being examined.
From the definition of Electric Flux, Gauss's Law may also be written equivalently as
[math]\displaystyle{ \Phi_{el} = \frac{Q_{enclosed}}{\varepsilon_{0}} }[/math]
Relation to Coulomb's Law
Additionally, Coulomb's Law and Gauss's Law are innately connected. Coulomb's Law relates charge to electric field. Gauss's Law relates charge to electric flux. Both laws, relate charge to an electrical property. For clarification, the electric flux is a quantity that is equal to the product of the perpendicular component of E-field and the area of the closed surface. Not only do these two laws look similar at the surface, but using one law it is quite easy to derive the other law.
Relationship Between Charge and Flux
We know from the previous introduction of flux that there is a relationship between the electric flux on a closed surface and the charges inside the surface. However, we would like to figure out what that particular factor is.
We start by considering a point charge of [math]\displaystyle{ +Q }[/math] enclosed by an imaginary spherical shell.
Everywhere on the imaginary shell, the electric field produced is parallel to the normal unit vector. Cos(0) = 1, so the dot product is simply the magnitude of the electric field. Recall that the surface area of the imaginary sphere is [math]\displaystyle{ 4 \pi r^{2} }[/math]. With Coulomb's Law and the surface area of a sphere, we get that electric flux is equal to [math]\displaystyle{ \frac{+Q}{\varepsilon_{0}} }[/math]. This implies that the factor is [math]\displaystyle{ \frac{1}{\varepsilon_{0}} }[/math].
Note that if the point charge was negative, the electric field would still be parallel, just opposite direction. Cos(180) = -1 so the dot product would be -1 times the magnitude of the electric field.
To understand this law more fully, one can look at the diagram below. As can be seen on the left side of this diagram, change in flux equals electric field multiplied by change in area. This is the basis for the equation ф=∮E da. When you integrate the change of A, you get the flux.
Image Taken from Hyperphysics
To more clearly state it, in integral form, the formula for this Law is the electric flux equals the total charge contained by a closed surface, divided by the permittivity ([math]\displaystyle{ \varepsilon_{0} = 8.854187817...×10^{-12} ~F*m^{-1} }[/math]).
Additionally, Gauss's law can be written in differential form.
In this equation, ρ is electric charge density, ∇*E is divergence of electric field, and [math]\displaystyle{ \varepsilon_{0} = 8.854187817...×10^{-12} ~F*m^{-1} }[/math].
Below is a brief summary of what has been covered.
A Computational Model
An extremely rudimentary explanation of Gauss's Law is: https://www.youtube.com/watch?v=f2Cccp6XBUY
To visualization of Gauss's law with computational model: https://www.youtube.com/watch?v=i5N36mWsdGo
Experimental demonstration of Gauss's law: https://www.youtube.com/watch?v=r3w4FAUOLuM
Visual explaination of Gauss Divergence Theorem(Khan Academy): https://www.youtube.com/watch?v=XyiQ2dwJHXE
To view the applications of Gauss's law in a coding setting (Python GLowScript): https://trinket.io/glowscript/f618920f61
Examples
Easy Examples
Easy Example 1
Looking at the images on the right hand side of the screen, we find an easy example in which we will find the electric field in a uniformly charged plate (+Q).
1. Recall Gauss's Formula:
2. Now look carefully at the diagram below and go through each of the surfaces one by one. Ask yourself, in what direction does the normal vector point?
3. Therefore, in the sides where there is 90 degree angle made with E, the flux will just be zero!
4. In the only case where the flux is not zero is in the sides A and B of the box (which are the same in magnitude). We compute the flux as follows:
Remember, when doing Gauss's problems, always think about you n vector before diving into the formula.
Easy Example 2
Consider a point charge [math]\displaystyle{ Q = +2 \, \text{μC} }[/math] enclosed by a spherical Gaussian surface with a radius of [math]\displaystyle{ r = 10 \, \text{cm} }[/math]. Calculate the electric flux through the surface.
- Solution:**
Using Gauss's Law, the electric flux [math]\displaystyle{ ( \Phi_{el} ) }[/math] through a closed surface is given by [math]\displaystyle{ \Phi_{el} = \frac{Q_{enclosed}}{\varepsilon_{0}} }[/math]. For a point charge enclosed by a spherical surface, the electric flux is simply [math]\displaystyle{ \frac{Q}{\varepsilon_{0}} }[/math]. Substituting the given values:
[math]\displaystyle{ \Phi_{el} = \frac{2 \times 10^{-6} \, \text{C}}{8.854 \times 10^{-12} \, \text{C}^2/\text{N}\cdot\text{m}^2} }[/math]
Intermediate Examples
Example 1
The example below shows how to determine the net charge located inside a box and is fundamental to understanding Gauss's Law. It demonstrates the idea that to calculate the net charge inside a box, we have to start off by calculating the fluxes acting on all surfaces on the box by using the Gauss's Law.
Example 2
The example below shows how to calculate the net charge enclosed by a box.
Example 3
In order to apply Gauss's Law, it is important to be certain you are working with a closed surface, then set electric flux equal to the internal field divided by the permittivity ([math]\displaystyle{ \varepsilon_{0} = 8.854187817...×10^{-12} ~F*m^{-1} }[/math]). An example of this Law being applied can be found below.
Example 4
In this example, the Qenc is equal to zero. This was determined by adding up all of the fluxes through every surface. This can also be determined by seeing that the same fluxes travel through the same areas of the tent. The equation Ф=∮B da=0 helps explain this when considering that Ф is the same in both equations.
Hard Examples
Example 1
Inside a non-uniformly charged sphere with a volume charge density [math]\displaystyle{ \rho(r) = \rho_0 r^2 }[/math] for [math]\displaystyle{ 0 \leq r \leq R }[/math], where [math]\displaystyle{ \rho_0 }[/math] is a constant and R is the radius of the sphere. Find the electric field at a distance r from the center, where r is between 0 and R, using Gauss's Law.
Solution:
To find the electric field inside the sphere, create a Gaussian surface and take advantage of the spherical symmetry. The charge enclosed within a Gaussian sphere of radius [math]\displaystyle{ r }[/math] is [math]\displaystyle{ \frac{4}{3}\pi \rho_0 r^3 }[/math]. Gauss's Law then gives [math]\displaystyle{ E = \frac{\rho_0 r}{3\varepsilon_0} }[/math].
Example 2
A long, straight wire carries a non-uniform linear charge density [math]\displaystyle{ \lambda(z) = \lambda_0 e^{-az} }[/math], where [math]\displaystyle{ \lambda_0 }[/math] and a are constants, and z is the distance along the wire. Determine the electric field at a distance r from the wire using Gauss's Law.
Solution:
Set up a Gaussian cylindrical surface around the wire to take advantage of the cylindrical symmetry. The total charge enclosed within the Gaussian surface is found by integrating the linear charge density along the length of the cylinder. Gauss's Law then gives [math]\displaystyle{ E = \frac{\lambda_0}{2\pi\varepsilon_0 r} \int_{-\infty}^{\infty} e^{-az} \, dz }[/math]. Solving this integral yields the expression for the electric field as a function of r.
Connectedness
Gauss's Law can be found in many areas of science, technology, engineering, and mathematics. In fact, Gauss's Law and other Maxwell Equations form a basis for electrodynamics. They are the fundamental core of this field of study. Gauss's Law is also connected to the Gaussian/Normal distribution, which is a continuous probability distribution that is characterized by a bell-shaped curve. This distribution is found throughout statistics and probability and is used everyday by people in STEM fields.
As Industrial and Systems Engineering majors, we deal with many statistical distributions. A very important fundamental distribution is the Gaussian distribution or the Normal Distribution. With inference, the Gaussian Distribution comes up in confidence intervals for single statistics. With comparison inference, like finding the pairwise difference between statistics, generally we use other distributions such as the T-Distribution. However, the T-Distribution approximates the Gaussian distribution with degrees of freedom greater than 29.
As civil and environmental engineering majors, we also deal with the Gaussian/Normal Distribution in our fields. As an example, the speed data of traffic on a highway is said to follow the normal distribution.
Additional to many engineering majors. Gauss's Law has applications in many different STEM job fields. Engineering majors learn about the different Gaussian laws in college and apply them in there jobs. Millions of people are applying his laws to the world and will continue to do so. Gauss has had a huge impact on the world and will continue to have a big impact on the future. Gauss has done great work with his work.
History
Gauss's Law was first 'discovered' in 1773, by the great mathematician Joseph-Louis Lagrange. It was further developed by Carl Friedrich Gauss in 1813. The law was inspired by Coulomb's law.
Gauss was a prolific German mathematician and physicist. He made significant contributions to a variety of fields in mathematics and physics. In fact his contributions are so great that he is referred to as the "greatest mathematician since antiquity" and the "foremost of mathematicians".
Gauss is also known for his advancements in the astronomy field. While the dwarf planet Ceres was discovered by Giuseppe Piazza (Italian astronomer), Gauss was able to predict the position for its rediscovery. Due to the methodology behind this rediscovery, Gauss's Method, there was also significant advancements in the theory of the motion of planetoids, which introduced the Gaussian gravitation constant.
The foundation for Gauss's law was laid by Isaac Newton, who formulated the inverse-square law of gravitation in 1687. This idea of forces diminishing with the square of distance inspired analogous formulations for electrostatics. In 1785, Charles-Augustin de Coulomb experimentally confirmed that electric forces between charges follow an inverse-square law. The concept of a field—an invisible influence extending through space—began to take shape in the late 18th and early 19th centuries. Mathematicians and physicists, including Joseph Priestley and others, laid groundwork for understanding how charges influence surrounding regions. Gauss formulated the law in his personal notes in 1835. These notes contained his ideas on how electric fields could be mathematically related to charges through surface integrals. His reluctance to publish might have been due to the lack of experimental confirmation at the time or his tendency to prioritize mathematical rigor over immediate dissemination. The law became widely known as part of James Clerk Maxwell’s unification of electromagnetic theory in the 1860s. Maxwell included Gauss’s law as one of his four foundational equations in Maxwell’s Equations. Although Maxwell credited earlier physicists, including Gauss, Faraday, and Ampère, the incorporation of Gauss’s law into a cohesive electromagnetic theory marked its formal introduction into mainstream physics. By the late 19th century, Gauss’s law was being taught in academic settings as a fundamental part of electrostatics and electromagnetism. It gained recognition in its integral and differential forms, largely through Maxwell’s equations and the broader development of vector calculus.
See also
Further Reading
Gauss's Law is tied in closely with the other of Maxwell's equations that can be found here in the Physics Book.
http://physicsbook.gatech.edu/Gauss%27s_Flux_Theorem
http://physicsbook.gatech.edu/Faraday%27s_Law
http://physicsbook.gatech.edu/Magnetic_Flux
http://physicsbook.gatech.edu/Ampere%27s_Law
External links
http://physics.info/law-gauss/
http://teacher.nsrl.rochester.edu/phy122/Lecture_Notes/Chapter24/Chapter24.html
https://en.wikipedia.org/wiki/Gauss%27s_law
https://en.wikipedia.org/wiki/Carl_Friedrich_Gauss
http://physicscatalyst.com/elec/guass_0.php
References
http://hyperphysics.phy-astr.gsu.edu/hbase/electric/gaulaw.html
http://www.pas.rochester.edu/~stte/phy114S09/lectures/lect04.pdf
http://www.sciencedirect.com/science/article/pii/S2090447911000165
spiff.rit.edu
study.com