Spring Motion: Difference between revisions
No edit summary |
No edit summary |
||
| (One intermediate revision by the same user not shown) | |||
| Line 14: | Line 14: | ||
When a mass is permanently attached to a mass, the mass' velocity increases as it approaches <math> L_0 </math> and decreases the further away it gets, causing an oscillation. In some cases, this may result in [[Simple Harmonic Motion]], in which the different aspects of the oscillation can be modeled and found trigonometric functions. For more information, see the linked page. | When a mass is permanently attached to a mass, the mass' velocity increases as it approaches <math> L_0 </math> and decreases the further away it gets, causing an oscillation. In some cases, this may result in [[Simple Harmonic Motion]], in which the different aspects of the oscillation can be modeled and found trigonometric functions. For more information, see the linked page. | ||
[[File:Animated-mass-spring.gif]] | |||
| Line 59: | Line 62: | ||
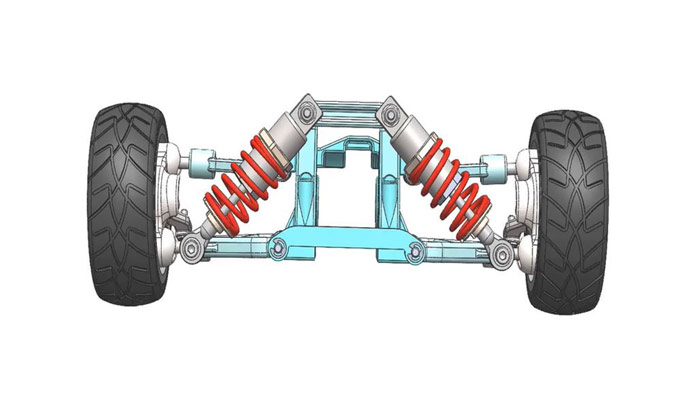
Spring motion plays a much bigger role in the movement of many objects than what might first meet the eye. Mattresses, Car Suspensions, Pens clicking their point in an out, even kangaroos jusmping around out in nature, all rely on this relationship between spring movement, displacement, and spring force. | Spring motion plays a much bigger role in the movement of many objects than what might first meet the eye. Mattresses, Car Suspensions, Pens clicking their point in an out, even kangaroos jusmping around out in nature, all rely on this relationship between spring movement, displacement, and spring force. | ||
[[File:Suspension-System.jpg] | [[File:Suspension-System.jpg]] | ||
Latest revision as of 19:31, 2 December 2025
by Caroline Ware
Edited by Adam Green, Fall 2025
Spring Motion
Spring motion is often used to describe the motion of a mass attached to a spring. Unlike what you may have encountered before, the net force acting on the mass is not constant, but is based on the amount that a spring is stretched or compressed. Every spring has it's own natural resting point, referred to as [math]\displaystyle{ L_0 }[/math] mathematically, which represents the length of the spring should the spring-mass system be at rest. When the length of the spring equals [math]\displaystyle{ L_0 }[/math], the force it would apply to an attached mass is zero. Although often referred to in a one dimensional setting, where all Force, Velocity, and Displacement are among one axis, Spring Motion and its related formulas can be used to describe both two and three dimensional movement as well.
If the length of the spring is changed from [math]\displaystyle{ L_0 }[/math], it results in a restorative force that attempts to restore the length of the spring to [math]\displaystyle{ L_0 }[/math]. Compressing the spring to make its length less than [math]\displaystyle{ L_0 }[/math] causes the spring to want to expand, pushing any attached object outward, and stretching the spring to make its length greater than [math]\displaystyle{ L_0 }[/math] results in a force pulling any attached object inward. Compressing the spring to make its length less than [math]\displaystyle{ L_0 }[/math] causes the spring to want to expand, pushing any attached object outward, and stretching the spring to make its length greater than [math]\displaystyle{ L_0 }[/math] results in a force pulling any attached object inward. Newton's First Law states that [math]\displaystyle{ F = ma }[/math], which means that the direction of the Force is the same as the direction of acceleration of the mass, meaning that the acceleration of the spring is always in the direction of [math]\displaystyle{ L_0 }[/math].
When a mass is permanently attached to a mass, the mass' velocity increases as it approaches [math]\displaystyle{ L_0 }[/math] and decreases the further away it gets, causing an oscillation. In some cases, this may result in Simple Harmonic Motion, in which the different aspects of the oscillation can be modeled and found trigonometric functions. For more information, see the linked page.
Mathematical Model
We can find the force that the spring is exerting on a mass using the formula: [math]\displaystyle{ F_{spring} = -k_s*s*L_{hat} }[/math], where [math]\displaystyle{ k_s }[/math] is the specific stiffness of the spring (how hard it is to stretch / compress), [math]\displaystyle{ s }[/math] is the difference in length of the spring from its current to relaxed length, found using the following equation [math]\displaystyle{ s= L - L_0 }[/math], and [math]\displaystyle{ L_{hat} }[/math] is the unit vector indicating the direction of the vector pointing from the spring's origin to the mass - essentially which direction the Force is pointing.
Spring motion can be predicted using the momentum principle [math]\displaystyle{ dp=F_{net}*dt }[/math] and the position-update formula [math]\displaystyle{ dr= p_f/m*dt }[/math] Because spring motion involves oscillation, it is important to iterate with a small enough change in time to capture the full path of the spring-mass system.
Spring Stiffness
The spring stiffness [math]\displaystyle{ k_s }[/math] is a constant specific to individual spring and is important for understanding the motion of a Spring, as it directly correlates to the magnitude of the restorative force. This mans that springs with greater spring stiffness have greater restorative force and typically a speedier contraction / expansion when compared to springs with a lesser spring stiffness. Combining springs effects their stiffness in different ways, however. If you attach two of the same spring in parallel (side by side), their combined stiffness is double that of the single spring. If you attach two of the same spring in series (one attached to the end of the other), however, the spring stiffness is halved
A Computational Model
The link below contains a model of spring motion among all three axes. The code displays a spring with one fixed end on a ceiling and a mass attached to the free end.
https://trinket.io/glowscript/3587ff8cbe
The pink arrow represents the magnitude and direction of the mass's momentum.
The yellow arrow represents the changing net force, Force of gravity + Force of the spring, on the mass (scaled down to 10%).
Examine the orange curve after the simulation ends to follow the path of the mass's motion.
Try an initial mass location to give a straight vertical path!
Phet Simulation
The following link contains a Phet simulation where you can test the impact of different factors on the motion of an oscillating spring, such as Spring Stiffness ([math]\displaystyle{ K }[/math]), Mass, and Gravitational Strength.
https://phet.colorado.edu/sims/html/masses-and-springs/latest/masses-and-springs_all.html
Connectedness
Spring motion plays a much bigger role in the movement of many objects than what might first meet the eye. Mattresses, Car Suspensions, Pens clicking their point in an out, even kangaroos jusmping around out in nature, all rely on this relationship between spring movement, displacement, and spring force.
History
Spring's have been around since the middle ages, with some of the earliest examples being ancient bows used for warfare. The spring coil, what we typically think of as a spring today, was invented and patented by Richard Tredwell. Robert Hooke was an early pioneer in studying the Physics of these spring's creating his famous law Hooke's law (linked below) in the late 17th Century, which states that [math]\displaystyle{ F = kx }[/math]. Rewritten, that gives us our spring force equation that we know and love today: [math]\displaystyle{ F_{spring} = -k_s*s*L_{hat} }[/math]
See also
Check out the Hooke's Law page to learn more about Hooke's Law Specifically.
Check out the Robert Hooke page to learn more about the life and discoveries of Robert Hooke.
Check out the Simple Harmonic Motion page to learn more about Simple Harmonic Motion.
Check out the Spring Force, Spring Potential Energy, Ball and Spring Model pages to learn more as well!
References
Elasticity. from http://www.one-school.net/Malaysia/UniversityandCollege/SPM/revisioncard/physics/forceandmotion/elasticity.html
Sound Propogation in Elastic Materials. from https://www.nde-ed.org/EducationResources/CommunityCollege/Ultrasonics/Physics/elasticsolids.htm
The Evolution and History of Springs, from https://www.jamesspring.com/news/history-of-springs/
Hooke's Law, from https://www.britannica.com/science/Hookes-law