Curly Electric Fields: Difference between revisions
| (19 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
''Written by Miranda Fyfe'' | |||
== | The '''Curly Electric Field''' is the non-Coulombic result of a changing current and time-varying magnetic field. | ||
==Definition== | |||
In the case where current in a solenoid is constant and magnetic force is likewise constant in time, it can be observed that the magnetic and electric forces experienced by some moving charge outside the solenoid are essentially zero. | In the case where current in a solenoid is constant and magnetic force is likewise constant in time, it can be observed that the magnetic and electric forces experienced by some moving charge outside the solenoid are essentially zero. | ||
However, in the situation where current in the solenoid is changing and magnetic force is thereby time-varying, a ''' | However, in the situation where current in the solenoid is changing and magnetic force is thereby time-varying, a '''Curly Electric Field''' can be observed. | ||
[[File:curlyefield2.png|275px|thumb|center|''The '''curly electric field''' curls around the axis of the solenoid'']] | [[File:curlyefield2.png|275px|thumb|center|''The '''curly electric field''' curls around the axis of the solenoid'']] | ||
| Line 15: | Line 17: | ||
==Proportionality== | ==Proportionality== | ||
This electric field is proportional to the rate of change of the magnetic field ( | This electric field is proportional to the rate of change of the magnetic field <math> ( \frac{\delta B}{\delta t} ) </math>. | ||
===Inside the solenoid=== | |||
Curly electric field is proportional to distance from the solenoid axis, ''r''. | Curly electric field is proportional to distance from the solenoid axis, ''r''. | ||
===Outside the solenoid=== | |||
Curly electric field is proportional to 1/''r'', with the field decreasing as distance from the axis increases. | Curly electric field is proportional to 1/''r'', with the field decreasing as distance from the axis increases. | ||
==The Non-Coulomb Curly Electric Field== | ==The Non-Coulomb Curly Electric Field== | ||
''Read more about [[non- | ''Read more about the [[Non-Coulomb Electric Field]]'' | ||
===Coulomb Electric Field=== | |||
Any electric field in accordance with Coulomb's law is said to be a ''Coulomb electric field''. | |||
Coulomb's Law: <math> \vec{E} = \frac{1}{4{\pi}{{\epsilon}_0}} \frac{q}{r^2} \hat{r} </math> | |||
===Non-Coulomb Electric Field=== | |||
An electric field associated with a time-varying magnetic field, i.e. the curly electric field. | |||
===Effect on charges=== | |||
The curly electric field has a standard effect on charges <math> ( \vec{F} = q\vec{E} ) </math> | |||
Because the curly electric field deals with non-stationary charges and the magnetic field and current are time-variant, the curly electric field is a '''Non-Coloumb Electric Field'''. | |||
==Direction of Curly Electric Field== | |||
===Faraday's Experiment=== | |||
[[File:faraday.png|300px|thumb|right|''The setup and observations from Faraday's experiment'']] | |||
In 1831, [[Michael Faraday]] conducted an experiment which proved magnetic fields could be produced by electric currents. The experiment involved connecting a battery to a large coiled wire, and measuring the effects with a voltmeter. Faraday recorded effects both upon first connecting the battery and when initially disconnecting it the later of which was found surprising. | |||
Because an effect could only be gauged when the magnetic field was changing, it was concluded that this effect was proportional to <math> ( \frac{\delta B}{\delta t} ) </math> | |||
===Finding the Direction=== | |||
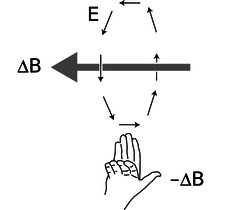
Implementing this proportion takes the process a step further; a [[Right Hand Rule]] can be utilized to pinpoint the direction of the curly electric field as follows: | |||
:Point the thumb of the right hand in the direction of <math> ( - \frac{\delta B}{\delta t} ) </math> , and curl the fingers in the direction of the curly electric field. | |||
[[File:rhr.png|250px|thumb|center|''The right hand rule for finding the direction of curly electric field'']] | |||
For each of the following four situations, the right hand rule can be used to determine direction of curly electric field. | |||
*Magnetic field out of the page and increasing <math> \rightarrow </math> Clockwise curly electric field | |||
*Magnetic field into the page and increasing <math> \rightarrow </math> Counterclockwise curly electric field | |||
*Magnetic field out of the page and decreasing <math> \rightarrow </math> Counterclockwise curly electric field | |||
*Magnetic field into the page and decreasing <math> \rightarrow </math> Clockwise curly electric field | |||
==Driving Current with Curly Electric Field== | |||
[[File:Currentinefield.png|250px|thumb|left|''The non-Coulombic curly electric field drives the current in the metal ring'']] | |||
The non-Coulombic curly electric field has the potential to create an effect akin to that of a battery; if a circular metal ring is placed around a solenoid with increasing magnetic field over time (see image), the curly electric field in the solenoid will drive the current in the metal ring clockwise. Further, as in an ordinary circuit, the current in the ring will be proportional to the electric field. | |||
===emf in Non-Coulomb Field=== | |||
The emf in a non-Coulomb field such as the curly electric field can be computed as the energy input per unit charge. Therefore the equation for emf in a non-Coulombic field is calculated thus: | |||
= | : <math> emf = \oint \vec{E}_{NC} \bullet {d}{\vec{l}} </math> | ||
====Outside Path==== | |||
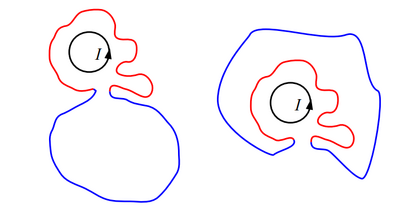
For any round-trip path that lies outside the solenoid--that is, it does not encircle the solenoid-- the emf is equal to zero. In the picture below, the path on the left ''does'' encircle the solenoid, and therefore has a nonzero emf. However, the rightmost path ''does not'' encircle the solenoid, and therefore that path has a zero emf value. | |||
[[File:encricleemf.png|400px|thumb|center|''When the solenoid is not encircled by the path, emf = 0'']] | |||
==== | ==External Links== | ||
*http://physwiki.ucdavis.edu/Fundamentals/11._Electromagnetism/11.5_Induced_Electric_Fields | |||
*http://www.phy.uct.ac.za/courses/opencontent/phy1004w/1004W%20EM%2022.pdf | |||
==References== | |||
#''Matter and Interactions'', Vol. 2 by Chabay and Sherwood | |||
#http://physwiki.ucdavis.edu/Fundamentals/11._Electromagnetism/11.5_Induced_Electric_Fields | |||
#http://www.phy.uct.ac.za/courses/opencontent/phy1004w/1004W%20EM%2022.pdf | |||
Latest revision as of 11:41, 2 December 2015
Written by Miranda Fyfe
The Curly Electric Field is the non-Coulombic result of a changing current and time-varying magnetic field.
Definition
In the case where current in a solenoid is constant and magnetic force is likewise constant in time, it can be observed that the magnetic and electric forces experienced by some moving charge outside the solenoid are essentially zero.
However, in the situation where current in the solenoid is changing and magnetic force is thereby time-varying, a Curly Electric Field can be observed.
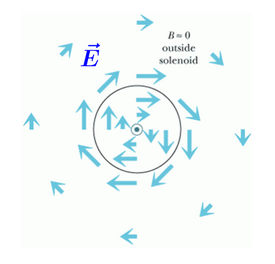
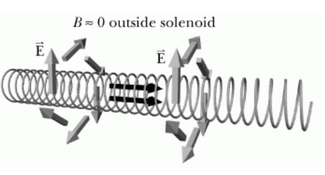
Proportionality
This electric field is proportional to the rate of change of the magnetic field [math]\displaystyle{ ( \frac{\delta B}{\delta t} ) }[/math].
Inside the solenoid
Curly electric field is proportional to distance from the solenoid axis, r.
Outside the solenoid
Curly electric field is proportional to 1/r, with the field decreasing as distance from the axis increases.
The Non-Coulomb Curly Electric Field
Read more about the Non-Coulomb Electric Field
Coulomb Electric Field
Any electric field in accordance with Coulomb's law is said to be a Coulomb electric field.
Coulomb's Law: [math]\displaystyle{ \vec{E} = \frac{1}{4{\pi}{{\epsilon}_0}} \frac{q}{r^2} \hat{r} }[/math]
Non-Coulomb Electric Field
An electric field associated with a time-varying magnetic field, i.e. the curly electric field.
Effect on charges
The curly electric field has a standard effect on charges [math]\displaystyle{ ( \vec{F} = q\vec{E} ) }[/math]
Because the curly electric field deals with non-stationary charges and the magnetic field and current are time-variant, the curly electric field is a Non-Coloumb Electric Field.
Direction of Curly Electric Field
Faraday's Experiment
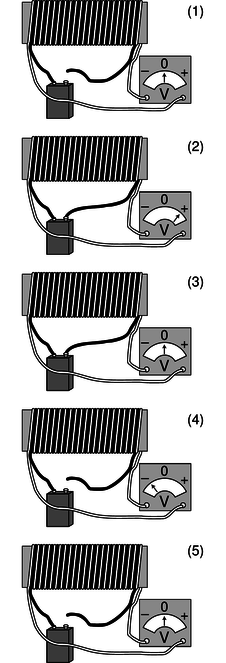
In 1831, Michael Faraday conducted an experiment which proved magnetic fields could be produced by electric currents. The experiment involved connecting a battery to a large coiled wire, and measuring the effects with a voltmeter. Faraday recorded effects both upon first connecting the battery and when initially disconnecting it the later of which was found surprising.
Because an effect could only be gauged when the magnetic field was changing, it was concluded that this effect was proportional to [math]\displaystyle{ ( \frac{\delta B}{\delta t} ) }[/math]
Finding the Direction
Implementing this proportion takes the process a step further; a Right Hand Rule can be utilized to pinpoint the direction of the curly electric field as follows:
- Point the thumb of the right hand in the direction of [math]\displaystyle{ ( - \frac{\delta B}{\delta t} ) }[/math] , and curl the fingers in the direction of the curly electric field.
For each of the following four situations, the right hand rule can be used to determine direction of curly electric field.
- Magnetic field out of the page and increasing [math]\displaystyle{ \rightarrow }[/math] Clockwise curly electric field
- Magnetic field into the page and increasing [math]\displaystyle{ \rightarrow }[/math] Counterclockwise curly electric field
- Magnetic field out of the page and decreasing [math]\displaystyle{ \rightarrow }[/math] Counterclockwise curly electric field
- Magnetic field into the page and decreasing [math]\displaystyle{ \rightarrow }[/math] Clockwise curly electric field
Driving Current with Curly Electric Field
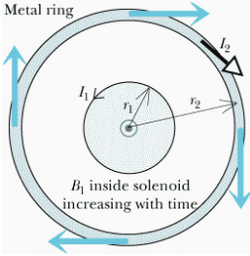
The non-Coulombic curly electric field has the potential to create an effect akin to that of a battery; if a circular metal ring is placed around a solenoid with increasing magnetic field over time (see image), the curly electric field in the solenoid will drive the current in the metal ring clockwise. Further, as in an ordinary circuit, the current in the ring will be proportional to the electric field.
emf in Non-Coulomb Field
The emf in a non-Coulomb field such as the curly electric field can be computed as the energy input per unit charge. Therefore the equation for emf in a non-Coulombic field is calculated thus:
- [math]\displaystyle{ emf = \oint \vec{E}_{NC} \bullet {d}{\vec{l}} }[/math]
Outside Path
For any round-trip path that lies outside the solenoid--that is, it does not encircle the solenoid-- the emf is equal to zero. In the picture below, the path on the left does encircle the solenoid, and therefore has a nonzero emf. However, the rightmost path does not encircle the solenoid, and therefore that path has a zero emf value.
External Links
- http://physwiki.ucdavis.edu/Fundamentals/11._Electromagnetism/11.5_Induced_Electric_Fields
- http://www.phy.uct.ac.za/courses/opencontent/phy1004w/1004W%20EM%2022.pdf
References
- Matter and Interactions, Vol. 2 by Chabay and Sherwood
- http://physwiki.ucdavis.edu/Fundamentals/11._Electromagnetism/11.5_Induced_Electric_Fields
- http://www.phy.uct.ac.za/courses/opencontent/phy1004w/1004W%20EM%2022.pdf