Franck-Hertz Experiment: Difference between revisions
Tbennett37 (talk | contribs) No edit summary |
Tbennett37 (talk | contribs) |
||
| (21 intermediate revisions by the same user not shown) | |||
| Line 21: | Line 21: | ||
[[File:Graph123.jpg]] [1] | [[File:Graph123.jpg]] [1] | ||
This is another way to visualize the different quantizations of an atom. This graph in particular shows the different levels of energy with the change of "r" or distance | This is another way to visualize the different quantizations of an atom. This graph in particular shows the different levels of energy with the change of "r" or distance from the proton. | ||
==Examples== | ==Examples== | ||
| Line 27: | Line 27: | ||
===Simple=== | ===Simple=== | ||
In this example, an electron has used all of its kinetic energy to excite a hydrogen atom from its first excited state to it’s second excited state. How much kinetic energy did the electron have? | |||
<math>E_{H*,f} = E_{H,i} + K_{e}</math> | |||
Since hydrogen has an energy of -13.6 eV at it’s ground state, we know that the same equation is equal to: | |||
<math>{\frac{-13.6 eV}{3^2}} = {\frac{-13.6 eV}{1^2}} + K_{e}</math> | |||
<math>K_{e} = 1.89 eV</math> | |||
===Middling=== | ===Middling=== | ||
An electron has now use a partial amount of its kinetic energy to excite a hydrogen atom from its ground level to its third excited state. If you are given the initial kinetic energy of the electron, can you find out how much energy is left over? | |||
<math>E_{H*,f} + K_{e,f} = E_{H,i} + K_{e, i}</math> | |||
The electron begins with 12.8 eV. | |||
<math>{\frac{-13.6 eV}{4^2}} + K_{e,f}= {\frac{-13.6 eV}{1^2}} + 12.8 eV</math> | |||
<math>K_{e,f} = 0.05 eV</math> | |||
===Difficult=== | ===Difficult=== | ||
We have only used hydrogen atoms in our examples. For this example, you will have a different (unknown) atom whose first excited state is 5.0 eV above the ground state and the second excited state is 7.5 eV above the ground level. The atom absorbed a photon, which means that all of the kinetic energy was used up, and it excited the electron to jump from the first excited state to the second excited state. How much energy did the photon begin with? | |||
Using the conservation of energy, we know that: | |||
<math>E_{f} = E_{i}</math> | |||
After plugging in our values and using <math>E_{0}</math> as the energy of the ground state, we see that: | |||
<math>(E_{0} + 5.0eV) + K_{photon} = (E_{0} + 7.5eV)</math> | |||
<math>K_{photon} = 2.5eV</math> | |||
==Connectedness== | ==Connectedness== | ||
The creation of this model has set the groundwork to almost everything we know today in modern technology. Our understanding of the atom and its behavior lead to the invention of the transistor, for example [4]. A transistor is a semiconductor with three connections which allow for amplification of a current [5]. This is what we use in today’s computers, cell phones, CD players, etc. Although we did have computers before this invention, previous models used vacuum tubes for logic element. | |||
A more simple example of the applications of this model is the understanding of the [[The Photoelectric Effect]]. This is the idea that when light hits an object, electrons are released in certain wavelengths that we see as color. | |||
==History== | ==History== | ||
| Line 49: | Line 83: | ||
===Further reading=== | ===Further reading=== | ||
<i>The Amazing Story of Quantum Mechanics: A Math-Free Exploration of the Science That Made Our World</i> by James Kakalios | |||
This book goes into detail of the discoveries in quantum physics and why it is so important to us today. Link [4] is an article that explains some of the broader questions that are discussed in the book. | |||
<i>Collisions between Electrons and Mercury Vapor Molecules and the Ionization Potential of Such Molecules</i> by James Franck and Gustav Hertz | |||
This is a short paper that Franck and Hertz published after their experiment. The link to this paper is link [6]. | |||
===External links=== | ===External links=== | ||
Here is a link to more information on James Franck: http://www.nobelprize.org/nobel_prizes/physics/laureates/1925/franck-bio.html | |||
Here is a link to more information on Gustav Hertz: http://www.nobelprize.org/nobel_prizes/physics/laureates/1925/hertz-bio.html | |||
Here is a link to a virtual lab that demonstrates the experiment: http://vlab.amrita.edu/?sub=1&brch=195&sim=355&cnt=1 | |||
==References== | ==References== | ||
| Line 62: | Line 106: | ||
[http://abyss.uoregon.edu/~js/glossary/bohr_atom.html] "Bohr Atomic Model." Bohr Atomic Model. Abyss. Web. 27 Nov. 2015. | [http://abyss.uoregon.edu/~js/glossary/bohr_atom.html] "Bohr Atomic Model." Bohr Atomic Model. Abyss. Web. 27 Nov. 2015. | ||
[http://www.scientificamerican.com/article/everyday-quantum-physics/] Matson, John. "What Is Quantum Mechanics Good For?" Scientific American Global RSS. Scientific American, A Division of Nature America, Inc., 2 Nov. 2010. Web. 2 Dec. 2015. | |||
[http://hyperphysics.phy-astr.gsu.edu/hbase/solids/trans.html] Nave, R. "Transistors." Hyper Physics. Hyper Physics. Web. 2 Dec. 2015. | |||
[http://www.if.ufrj.br/~maximo/Lab-1_arquivos/Franck-Hertz_Colisions-electrons-Hg.pdf] Franck, James, and Gustav Hertz. "Collisions between Electrons and Mercury Vapor Molecules and the Ionization Potential of Such Molecules." (1914): 770-78. Print. | |||
[[Category:Energy]] | [[Category:Energy]] | ||
Latest revision as of 12:21, 2 December 2015
Claimed and created by Tyler Bennett
Main Idea
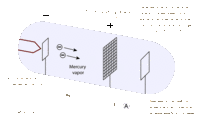
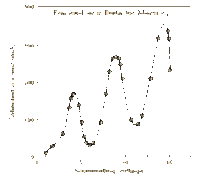
James Franck and Gustav Hertz were German physicists that helped to prove the Quantum Theory using their collisional excitation experiment in 1914. The quantum theory states that atoms have discrete levels made up of electrons of specific kinetic energies for each level. To confirm this, the Franck-Hertz duo created an accelerating apparatus, which simply sends electrons with varying kinetic energies through a vapor (in this case, mercury vapor) and then collects the electrons that weren’t picked up by the atoms using a collector. The results showed that once the electrons reached the threshold kinetic energy of 4.9 eV, most of them were picked up by the atoms, and they didn’t reach the collector [2]. This proved that the first level of the mercury atoms needs electrons with at least 4.9 eV to be absorbed. This technique was used with other elements to find their own threshold kinetic energies.
A Mathematical Model
where [math]\displaystyle{ E_{H*, f} }[/math] is the final energy of the atom plus the energy of the electrons and [math]\displaystyle{ K_{e, f} }[/math] is the final energy left over by the passing electrons. [math]\displaystyle{ E_{H, i} }[/math] and [math]\displaystyle{ K_{e,i} }[/math] are the initial quantities of the atom and the electron before the collision of the two or before the absorption of the photon. This equation is consistent with conservation of energy, meaning that there is no loss or gain of energy from outside of the system.
- For example [math]\displaystyle{ {\frac{d\vec{p}}{dt}}_{system} = \vec{F}_{net} }[/math] where p is the momentum of the system and F is the net force from the surroundings.
A Computational Model
This image is an accurate visualization of how electrons could jump to different levels or be "excited" to the next level. "n=1" is called the ground level, "n=2" is called the first excited state. "n=2" is called the second excited state, and so on.
This is another way to visualize the different quantizations of an atom. This graph in particular shows the different levels of energy with the change of "r" or distance from the proton.
Examples
Be sure to show all steps in your solution and include diagrams whenever possible
Simple
In this example, an electron has used all of its kinetic energy to excite a hydrogen atom from its first excited state to it’s second excited state. How much kinetic energy did the electron have?
[math]\displaystyle{ E_{H*,f} = E_{H,i} + K_{e} }[/math]
Since hydrogen has an energy of -13.6 eV at it’s ground state, we know that the same equation is equal to:
[math]\displaystyle{ {\frac{-13.6 eV}{3^2}} = {\frac{-13.6 eV}{1^2}} + K_{e} }[/math]
[math]\displaystyle{ K_{e} = 1.89 eV }[/math]
Middling
An electron has now use a partial amount of its kinetic energy to excite a hydrogen atom from its ground level to its third excited state. If you are given the initial kinetic energy of the electron, can you find out how much energy is left over?
[math]\displaystyle{ E_{H*,f} + K_{e,f} = E_{H,i} + K_{e, i} }[/math]
The electron begins with 12.8 eV.
[math]\displaystyle{ {\frac{-13.6 eV}{4^2}} + K_{e,f}= {\frac{-13.6 eV}{1^2}} + 12.8 eV }[/math]
[math]\displaystyle{ K_{e,f} = 0.05 eV }[/math]
Difficult
We have only used hydrogen atoms in our examples. For this example, you will have a different (unknown) atom whose first excited state is 5.0 eV above the ground state and the second excited state is 7.5 eV above the ground level. The atom absorbed a photon, which means that all of the kinetic energy was used up, and it excited the electron to jump from the first excited state to the second excited state. How much energy did the photon begin with?
Using the conservation of energy, we know that:
[math]\displaystyle{ E_{f} = E_{i} }[/math]
After plugging in our values and using [math]\displaystyle{ E_{0} }[/math] as the energy of the ground state, we see that:
[math]\displaystyle{ (E_{0} + 5.0eV) + K_{photon} = (E_{0} + 7.5eV) }[/math]
[math]\displaystyle{ K_{photon} = 2.5eV }[/math]
Connectedness
The creation of this model has set the groundwork to almost everything we know today in modern technology. Our understanding of the atom and its behavior lead to the invention of the transistor, for example [4]. A transistor is a semiconductor with three connections which allow for amplification of a current [5]. This is what we use in today’s computers, cell phones, CD players, etc. Although we did have computers before this invention, previous models used vacuum tubes for logic element.
A more simple example of the applications of this model is the understanding of the The Photoelectric Effect. This is the idea that when light hits an object, electrons are released in certain wavelengths that we see as color.
History
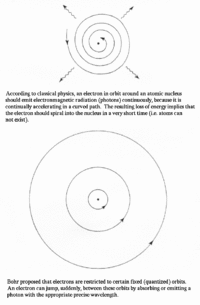
In 1911, Ernest Rutherford created a model of the atom which was proven wrong in the next couple of years. His model displayed only a single level that spiraled about the nucleus of the atom. Niels Bohr noted that this model would mean that atoms could not exist, as the electrons would spiral into the nucleus. Bohr then came up with his own model in 1913 that consisted of different shells outside of the atom. The electrons could jump shells and they would have constant quantized orbits. The Franck-Hertz experiment confirmed this model in showing that atoms can only obtain electrons when they contain enough kinetic energy to be able to jump onto the atoms’ shells.
See also
Further reading
The Amazing Story of Quantum Mechanics: A Math-Free Exploration of the Science That Made Our World by James Kakalios
This book goes into detail of the discoveries in quantum physics and why it is so important to us today. Link [4] is an article that explains some of the broader questions that are discussed in the book.
Collisions between Electrons and Mercury Vapor Molecules and the Ionization Potential of Such Molecules by James Franck and Gustav Hertz
This is a short paper that Franck and Hertz published after their experiment. The link to this paper is link [6].
External links
Here is a link to more information on James Franck: http://www.nobelprize.org/nobel_prizes/physics/laureates/1925/franck-bio.html
Here is a link to more information on Gustav Hertz: http://www.nobelprize.org/nobel_prizes/physics/laureates/1925/hertz-bio.html
Here is a link to a virtual lab that demonstrates the experiment: http://vlab.amrita.edu/?sub=1&brch=195&sim=355&cnt=1
References
[1] Chabay, Ruth W., and Bruce A. Sherwood. "Energy Quantization." Matter & Interactions. 3rd ed. Hoboken: Wiley, 2011. Print.
[2] Nave, R. "The Franck-Hertz Experiment." Hyper Physics. Hyper Physics. Web. 27 Nov. 2015.
[3] "Bohr Atomic Model." Bohr Atomic Model. Abyss. Web. 27 Nov. 2015.
[4] Matson, John. "What Is Quantum Mechanics Good For?" Scientific American Global RSS. Scientific American, A Division of Nature America, Inc., 2 Nov. 2010. Web. 2 Dec. 2015.
[5] Nave, R. "Transistors." Hyper Physics. Hyper Physics. Web. 2 Dec. 2015.
[6] Franck, James, and Gustav Hertz. "Collisions between Electrons and Mercury Vapor Molecules and the Ionization Potential of Such Molecules." (1914): 770-78. Print.


