AC: Difference between revisions
Bmwalker2005 (talk | contribs) |
Bmwalker2005 (talk | contribs) |
||
| (39 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
This topic covers '''AC (Alternating Current)'''. Claimed by bwalker60 | This topic covers '''AC (Alternating Current)'''. Claimed by Bryson Walker (bwalker60) | ||
==The Main Idea== | ==The Main Idea== | ||
| Line 16: | Line 16: | ||
In an AC circuit the current does not need to be in phase with the voltage, meaning the current and voltage of the circuit do not necessarily peak or reach their maximum/minimum values at the same time. If the voltage peaks later than the current in an AC circuit it is said that the current in the circuit "leads" the applied voltage. | In an AC circuit the current does not need to be in phase with the voltage, meaning the current and voltage of the circuit do not necessarily peak or reach their maximum/minimum values at the same time. If the voltage peaks later than the current in an AC circuit it is said that the current in the circuit "leads" the applied voltage. | ||
[[File:AC_phase_shift.gif]] | |||
===A Mathematical Model=== | ===A Mathematical Model=== | ||
'''Root Means Square Voltage''' | '''Root Means Square Voltage''' | ||
<math>\Delta V_{rms}</math> is the Root Means Square voltage of an AC circuit. This represents the voltage at which a DC circuit would produce the same power as the AC circuit with voltage <math>V_{rms}</math> | |||
RMS Voltage For a Sinusoidal AC circuit: | |||
<math>\Delta V_{rms} = {\sqrt{\frac{1}{2}}} \Delta V_{max}</math> | <math>\Delta V_{rms} = {\sqrt{\frac{1}{2}}} \Delta V_{max}</math> | ||
| Line 25: | Line 31: | ||
'''Average Power''' | '''Average Power''' | ||
<math>P_{avg}</math> is the average power an AC circuit can produce with a given Root Means Square Voltage. | |||
<math>P_{avg} = {\frac{\Delta V_{rms}^2}{R}}</math> | <math>P_{avg} = {\frac{\Delta V_{rms}^2}{R}}</math> | ||
| Line 30: | Line 38: | ||
'''Phase Angle''' | '''Phase Angle''' | ||
<math>\phi</math> represents the Phase Angle of an AC circuit which is the offset value causing the Phase Shift between applied voltage and current in a sinusoidal AC circuit. | |||
<math>\tan( \phi) = {\frac{1}{RC \omega}}</math> | <math>\tan( \phi) = {\frac{1}{RC \omega}}</math> | ||
| Line 35: | Line 45: | ||
'''Max Current''' | '''Max Current''' | ||
This represents the maximum current an AC circuit can achieve given the maximum applied Voltage. | |||
<math>I_{max} = \frac{\Delta V_{max}}{\sqrt{R^2 + \frac{1}{(C \omega)^2}}}</math> | <math>I_{max} = \frac{\Delta V_{max}}{\sqrt{R^2 + \frac{1}{(C \omega)^2}}}</math> | ||
| Line 40: | Line 52: | ||
===A Computational Model=== | ===A Computational Model=== | ||
The below image depicts the current of both a DC circuit and an AC circuit. It accurately shows how the current of the DC circuit (right) is constantly moving in one direction while the current of the AC circuit (left) is constantly shifting its direction. | |||
[[File:Ac-vs-dc-o.gif]] | |||
==Examples== | ==Examples== | ||
===Simple=== | |||
A power-line carrying a sinusoidal AC voltage with maximum of 325 V is traveling across the city. What is the DC voltage of equivalent power? | |||
<math>\Delta V_{rms} = {\sqrt{\frac{1}{2}}} \Delta V_{max}</math> | |||
With <math>V_{max}</math> 325 V, the DC voltage of equivalent power is <math>325V* \sqrt{\frac{1}{2}}</math> which is approximately 230 V. | |||
===Middling=== | ===Middling=== | ||
What is the average power of an AC circuit with maximum voltage of 325 V and two 6 ohm resistors in series? | |||
<math>P_{avg} = {\frac{\Delta V_{rms}^2}{R}}</math> | |||
<math>\Delta V_{rms} = {\sqrt{\frac{1}{2}}} \Delta V_{max}</math> | |||
With <math>V_{max}</math> 325 V, the <math>\Delta V_{rms}</math> is <math>325V* \sqrt{\frac{1}{2}}</math> which is approximately 230 V. | |||
With <math>\Delta V_{rms}</math> 230 V and resistance R of <math>2 * 6</math> ohms = <math>12</math> ohms, the average power of the circuit is <math>P_{avg} = {\frac{230^2}{12}}</math> which is approximately 4.4 KW. | |||
===Difficult=== | ===Difficult=== | ||
What is the maximum current of an RC circuit with 2 6 ohm resistors in series with a 2 farad capacitor, powered by 110 V AC at the U.S standard frequency? | |||
We find this value using this equation: | |||
<math>I_{max} = \frac{\Delta V_{max}}{\sqrt{R^2 + \frac{1}{(C \omega)^2}}}</math> | |||
C is given (2 farads); R, <math>V_{max}</math>, and <math>\omega</math> must be calculated. | |||
R = # resistors * resistance. | |||
<math>R = 2 * 6 = 12</math> ohms | |||
<math>V_{max} = \sqrt{2} V_{rms}</math> | |||
<math>V_{max} = \sqrt{2} * 110 = 155</math> V | |||
<math>\omega = \frac{2\pi}{T}</math> | |||
<math>T = \frac{1}{f}</math> | |||
U.S standard frequency is 60 hz. | |||
<math>T = \frac{1}{60} = .01667</math> seconds | |||
<math>\omega = \frac{2\pi}{.01667} = 376.92</math> rads/sec | |||
<math>I_{max} = \frac{155}{\sqrt{12^2 + \frac{1}{(2 * 376.92)^2}}} = 12.917</math> amperes | |||
==Connectedness== | ==Connectedness== | ||
# | #Alternating Current is the method by which most modern day appliances are powered. All electricity delivered to and running through most residential and commercial buildings are driven by alternating current. | ||
# | #Computers have internal power supply components which convert the alternating current they receive from outlets into a direct current it needs to function properly. | ||
# | #Alternating current was the most efficient way to deliver power across power lines through transformers when power lines were initially laid. | ||
==History== | ==History== | ||
Put this idea in historical context. Give the reader the Who, What, When, Where, and Why. | Put this idea in historical context. Give the reader the Who, What, When, Where, and Why. | ||
In 1835, Hippolyte Pixii built the first alternator, a device used to generate alternating current. Due to most other experimenters of the time working on DC devices, he had no uses or ideas for the device. | |||
In 1879, Walter Baily invented an early, extremely weak version of an AC motor with very little applicable use. | |||
In 1885, Galileo Ferraris theorized the first polyphase AC motor. | |||
In 1888, Ferraris published his report on his idea for a polyphase AC motor which made the AC motor much more efficient and finally competitive with DC motors. | |||
In the same year, nearly a month later, Nikola Tesla displays his polyphase motor before the AIEE and claims to have come up with the idea before Ferraris. Later a U.S court sides with him on the basis of witness testimony and from there on out, Tesla was known as the "Father of AC." | |||
By the 1900s, three phase AC power was established as the main source of power in the world. | |||
See http://www.edisontechcenter.org/AC-PowerHistory.html for a more detailed history timeline of AC power. | |||
== See also == | == See also == | ||
*[[Current]] | |||
===Further reading=== | ===Further reading=== | ||
Books, Articles or other print media on this topic | Books, Articles or other print media on this topic | ||
*Willam A. Meyers, History and Reflections on the Way Things Were: Mill Creek Power Plant – Making History with AC, IEEE Power Engineering Review, February 1997, pages 22–24 | |||
*Duff, John R., and Stephen L. Herman. Alternating Current Fundamentals. Albany, NY: Delmar, 2000. Print | |||
===External links=== | ===External links=== | ||
| Line 71: | Line 150: | ||
Internet resources on this topic | Internet resources on this topic | ||
http://www.allaboutcircuits.com/textbook/alternating-current/#chpt-1 | *http://www.allaboutcircuits.com/textbook/alternating-current/#chpt-1 | ||
*https://nationalmaglab.org/education/magnet-academy/watch-play/interactive/alternating-current-1 | |||
*http://hyperphysics.phy-astr.gsu.edu/hbase/electric/accircon.html#c1 | |||
==References== | ==References== | ||
| Line 79: | Line 160: | ||
This section contains the the references you used while writing this page | This section contains the the references you used while writing this page | ||
Chabay, Ruth W., and Bruce A. Sherwood. "Ch 19 Section 9: "*What Are AC and DC?"" Matter & Interactions. Electric and Magnetic Interactions. Hoboken, NJ: Wiley, 2011. N. pag. Print. | *Chabay, Ruth W., and Bruce A. Sherwood. "Ch 19 Section 9: "*What Are AC and DC?"" Matter & Interactions. Electric and Magnetic Interactions. Hoboken, NJ: Wiley, 2011. N. pag. Print. | ||
*"Vol. II - Alternating Current (AC)." - Electronics Textbook. N.p., n.d. Web. 01 Dec. 2015. <http://www.allaboutcircuits.com/textbook/alternating-current/#chpt-1>. | |||
*"Alternating Current - MagLab." Alternating Current - MagLab. N.p., n.d. Web. 01 Dec. 2015. <https://nationalmaglab.org/education/magnet-academy/watch-play/interactive/alternating-current-1> | |||
" | *Whelan, M., Joseph Cunningham, and S. Rockwell. "AC Power History and Timeline." AC Power History. Edison Tech Center, n.d. Web. 01 Dec. 2015. <http://www.edisontechcenter.org/AC-PowerHistory.html>. | ||
" | *Samskie. "AC vs DC." GifSoup. Gif Soup, 2011. Web. 01 Dec. 2015. <http://gifsoup.com/view/3719324/ac-vs-dc.html>. | ||
*"Phase." HyperPhysics. Hyper Physics, n.d. Web. 1 Dec. 2015. <http://hyperphysics.phy-astr.gsu.edu/hbase/electric/phase.html>. | |||
[[Category:Simple Circuits]] | [[Category:Simple Circuits]] | ||
Latest revision as of 19:53, 2 December 2015
This topic covers AC (Alternating Current). Claimed by Bryson Walker (bwalker60)
The Main Idea
Alternating current is a varying current driven by varying voltages. This means the current is constantly changing (in both magnitude and direction) as a function of time. This is opposed by Direct Current, in which the current is constant and non-varying in either direction or magnitude.
Alternating current powers most appliances in residential and commercial areas. The wall outlets found in homes are connected to alternating current circuits. Alternating current is the predominant power source for most residential areas in order to efficiently and easily convert high AC voltages (straight from the power plant) to lower AC voltages (used in residential areas by appliances). Until recently, conversion from high DC voltages to low DC voltages was quite difficult and inefficient.
Alternating current is typically found in a sine wave function pattern. In the U.S, the standard power-line frequency is 60 hertz, meaning the AC voltage oscillates completely 60 times per second. In most European countries the standard power-line frequency is 50 hertz.
AC Power
An AC circuit that varies in a sine waveform between -155 V and +155 V is called a "110 volts AC" circuit because it delivers the same amount of energy in one second as a constant (DC) circuit at 110 V. This is an example that the average power of an AC circuit is less than the power of an equivalent maximum voltage DC circuit.
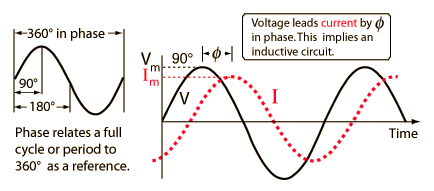
Phase Shift
In an AC circuit the current does not need to be in phase with the voltage, meaning the current and voltage of the circuit do not necessarily peak or reach their maximum/minimum values at the same time. If the voltage peaks later than the current in an AC circuit it is said that the current in the circuit "leads" the applied voltage.
A Mathematical Model
Root Means Square Voltage
[math]\displaystyle{ \Delta V_{rms} }[/math] is the Root Means Square voltage of an AC circuit. This represents the voltage at which a DC circuit would produce the same power as the AC circuit with voltage [math]\displaystyle{ V_{rms} }[/math]
RMS Voltage For a Sinusoidal AC circuit:
[math]\displaystyle{ \Delta V_{rms} = {\sqrt{\frac{1}{2}}} \Delta V_{max} }[/math]
Average Power
[math]\displaystyle{ P_{avg} }[/math] is the average power an AC circuit can produce with a given Root Means Square Voltage.
[math]\displaystyle{ P_{avg} = {\frac{\Delta V_{rms}^2}{R}} }[/math]
Phase Angle
[math]\displaystyle{ \phi }[/math] represents the Phase Angle of an AC circuit which is the offset value causing the Phase Shift between applied voltage and current in a sinusoidal AC circuit.
[math]\displaystyle{ \tan( \phi) = {\frac{1}{RC \omega}} }[/math]
Max Current
This represents the maximum current an AC circuit can achieve given the maximum applied Voltage.
[math]\displaystyle{ I_{max} = \frac{\Delta V_{max}}{\sqrt{R^2 + \frac{1}{(C \omega)^2}}} }[/math]
A Computational Model
The below image depicts the current of both a DC circuit and an AC circuit. It accurately shows how the current of the DC circuit (right) is constantly moving in one direction while the current of the AC circuit (left) is constantly shifting its direction.
Examples
Simple
A power-line carrying a sinusoidal AC voltage with maximum of 325 V is traveling across the city. What is the DC voltage of equivalent power?
[math]\displaystyle{ \Delta V_{rms} = {\sqrt{\frac{1}{2}}} \Delta V_{max} }[/math]
With [math]\displaystyle{ V_{max} }[/math] 325 V, the DC voltage of equivalent power is [math]\displaystyle{ 325V* \sqrt{\frac{1}{2}} }[/math] which is approximately 230 V.
Middling
What is the average power of an AC circuit with maximum voltage of 325 V and two 6 ohm resistors in series?
[math]\displaystyle{ P_{avg} = {\frac{\Delta V_{rms}^2}{R}} }[/math]
[math]\displaystyle{ \Delta V_{rms} = {\sqrt{\frac{1}{2}}} \Delta V_{max} }[/math]
With [math]\displaystyle{ V_{max} }[/math] 325 V, the [math]\displaystyle{ \Delta V_{rms} }[/math] is [math]\displaystyle{ 325V* \sqrt{\frac{1}{2}} }[/math] which is approximately 230 V.
With [math]\displaystyle{ \Delta V_{rms} }[/math] 230 V and resistance R of [math]\displaystyle{ 2 * 6 }[/math] ohms = [math]\displaystyle{ 12 }[/math] ohms, the average power of the circuit is [math]\displaystyle{ P_{avg} = {\frac{230^2}{12}} }[/math] which is approximately 4.4 KW.
Difficult
What is the maximum current of an RC circuit with 2 6 ohm resistors in series with a 2 farad capacitor, powered by 110 V AC at the U.S standard frequency?
We find this value using this equation:
[math]\displaystyle{ I_{max} = \frac{\Delta V_{max}}{\sqrt{R^2 + \frac{1}{(C \omega)^2}}} }[/math]
C is given (2 farads); R, [math]\displaystyle{ V_{max} }[/math], and [math]\displaystyle{ \omega }[/math] must be calculated.
R = # resistors * resistance.
[math]\displaystyle{ R = 2 * 6 = 12 }[/math] ohms
[math]\displaystyle{ V_{max} = \sqrt{2} V_{rms} }[/math]
[math]\displaystyle{ V_{max} = \sqrt{2} * 110 = 155 }[/math] V
[math]\displaystyle{ \omega = \frac{2\pi}{T} }[/math]
[math]\displaystyle{ T = \frac{1}{f} }[/math]
U.S standard frequency is 60 hz.
[math]\displaystyle{ T = \frac{1}{60} = .01667 }[/math] seconds
[math]\displaystyle{ \omega = \frac{2\pi}{.01667} = 376.92 }[/math] rads/sec
[math]\displaystyle{ I_{max} = \frac{155}{\sqrt{12^2 + \frac{1}{(2 * 376.92)^2}}} = 12.917 }[/math] amperes
Connectedness
- Alternating Current is the method by which most modern day appliances are powered. All electricity delivered to and running through most residential and commercial buildings are driven by alternating current.
- Computers have internal power supply components which convert the alternating current they receive from outlets into a direct current it needs to function properly.
- Alternating current was the most efficient way to deliver power across power lines through transformers when power lines were initially laid.
History
Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.
In 1835, Hippolyte Pixii built the first alternator, a device used to generate alternating current. Due to most other experimenters of the time working on DC devices, he had no uses or ideas for the device.
In 1879, Walter Baily invented an early, extremely weak version of an AC motor with very little applicable use.
In 1885, Galileo Ferraris theorized the first polyphase AC motor.
In 1888, Ferraris published his report on his idea for a polyphase AC motor which made the AC motor much more efficient and finally competitive with DC motors. In the same year, nearly a month later, Nikola Tesla displays his polyphase motor before the AIEE and claims to have come up with the idea before Ferraris. Later a U.S court sides with him on the basis of witness testimony and from there on out, Tesla was known as the "Father of AC."
By the 1900s, three phase AC power was established as the main source of power in the world.
See http://www.edisontechcenter.org/AC-PowerHistory.html for a more detailed history timeline of AC power.
See also
Further reading
Books, Articles or other print media on this topic
- Willam A. Meyers, History and Reflections on the Way Things Were: Mill Creek Power Plant – Making History with AC, IEEE Power Engineering Review, February 1997, pages 22–24
- Duff, John R., and Stephen L. Herman. Alternating Current Fundamentals. Albany, NY: Delmar, 2000. Print
External links
Internet resources on this topic
References
This section contains the the references you used while writing this page
- Chabay, Ruth W., and Bruce A. Sherwood. "Ch 19 Section 9: "*What Are AC and DC?"" Matter & Interactions. Electric and Magnetic Interactions. Hoboken, NJ: Wiley, 2011. N. pag. Print.
- "Vol. II - Alternating Current (AC)." - Electronics Textbook. N.p., n.d. Web. 01 Dec. 2015. <http://www.allaboutcircuits.com/textbook/alternating-current/#chpt-1>.
- "Alternating Current - MagLab." Alternating Current - MagLab. N.p., n.d. Web. 01 Dec. 2015. <https://nationalmaglab.org/education/magnet-academy/watch-play/interactive/alternating-current-1>
- Whelan, M., Joseph Cunningham, and S. Rockwell. "AC Power History and Timeline." AC Power History. Edison Tech Center, n.d. Web. 01 Dec. 2015. <http://www.edisontechcenter.org/AC-PowerHistory.html>.
- Samskie. "AC vs DC." GifSoup. Gif Soup, 2011. Web. 01 Dec. 2015. <http://gifsoup.com/view/3719324/ac-vs-dc.html>.
- "Phase." HyperPhysics. Hyper Physics, n.d. Web. 1 Dec. 2015. <http://hyperphysics.phy-astr.gsu.edu/hbase/electric/phase.html>.