Generator: Difference between revisions
(→Simple) |
|||
| (5 intermediate revisions by the same user not shown) | |||
| Line 15: | Line 15: | ||
===Simple=== | ===Simple=== | ||
The diagram below shows a generator. When the coil is rotated around the axle, a current is produced and the lamp lights up. | The diagram below shows a generator. The magnets produce magnetic field '''B'''. When the coil of area '''A''' is rotated around the axle, a current is produced and the lamp lights up. | ||
[[File:Diagram3.png |center|]] | |||
a) When the magnetic field forms angle theta = omega*t with the normal of the loop, calculate the '''emf''' produced by the generator | a) When the magnetic field forms angle theta = omega*t with the normal of the loop, calculate the '''emf''' produced by the generator | ||
b) Assuming negligale resistance in the wires, what is the current '''I''' through the circut when the lightbulb filament has resistance a '''R'''. | b) Assuming negligale resistance in the wires, what is the current '''I''' through the circut when the lightbulb filament has resistance a '''R'''. | ||
[[File:SimpleSolution.png |center|frame| Answer]] | |||
===Difficult=== | ===Difficult=== | ||
A metal bar of mass '''M''' and length '''L''' slides with negligable friction but good electrical contact down between two verticle metal posts. The bar falls at a constant speed '''v'''. The falling ball and verticle metal posts have negligable electrical resistance, but the bottom rod is a resistor with resistance '''R'''. Throughout the entire region there is a uniform magnetic field with magnitude '''B''' coming towards the viewer perpindicular to the bar system. | |||
A) Calculate the amount of current '''I'''running through the resister. | |||
B) On a diagram, clearly show the surface charge distribution all the way around the circuit and the direction of the conventional current '''I'''. | |||
C) Calculate the constant speed '''v''' of the falling bar. | |||
[[File:DifficultSolution.png |center|frame| Answer]] | |||
==Connectedness== | ==Connectedness== | ||
Latest revision as of 00:14, 4 December 2015
This page is about how Electric Generators convert mechanical energy into electric energy.
The Main Idea
In electromagnetics, a generator is a device that takes mechanical energy and converts it into electric energy. Thanks to Faraday's Laws of Motional EMF, it is possible to induce EMF in a conductor by moving it through a magnetic field. If that conductor is connected to a complete circut, the conductor will act like a battery and create an electric current in the circut.

A Mathematical Model
The current produced by the generator can be found by the two simple formulas I = emf/R and emf = Df/dt. Df/dt is the change in magnetic flux over time.
Examples
Simple
The diagram below shows a generator. The magnets produce magnetic field B. When the coil of area A is rotated around the axle, a current is produced and the lamp lights up.
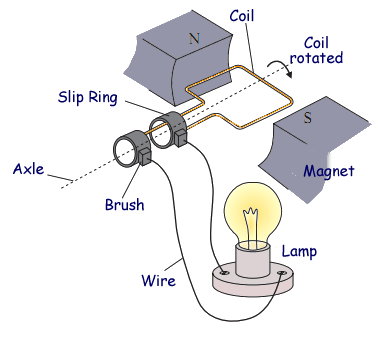
a) When the magnetic field forms angle theta = omega*t with the normal of the loop, calculate the emf produced by the generator
b) Assuming negligale resistance in the wires, what is the current I through the circut when the lightbulb filament has resistance a R.

Difficult
A metal bar of mass M and length L slides with negligable friction but good electrical contact down between two verticle metal posts. The bar falls at a constant speed v. The falling ball and verticle metal posts have negligable electrical resistance, but the bottom rod is a resistor with resistance R. Throughout the entire region there is a uniform magnetic field with magnitude B coming towards the viewer perpindicular to the bar system.
A) Calculate the amount of current Irunning through the resister.
B) On a diagram, clearly show the surface charge distribution all the way around the circuit and the direction of the conventional current I.
C) Calculate the constant speed v of the falling bar.
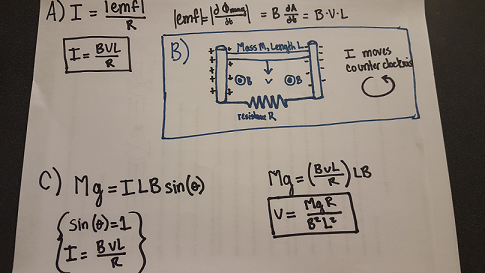
Connectedness
- This topic related to the production of Energy which interests me because I intend to go into Aternative Energies.
- This is related to Electrical Engineering because it deals with the generation of electricity.
- Generators are the interesting intustrial application of Faraday's Laws
History
Around 1870, after electricity had been around for a while, scientists wanted to find a way to use Faraday's Laws to generate electricity. First they came up with the DC generator, which creates a Direct Current. A little while later the AC generator, which produces Alternating Current, was developed.
Thomas Eddison used the DC generator in his creation of the lightbulb because of the avalibility of DC generators and moters. The DC current worked fine for small scale power, but it was a poor way to transport electricity over long distances. After Nikola Tesela invented a working AC motar and improved the AC generator, power companies were able to generate and distribute larger scale electricity.
According to Legend, Thomas Eddison strongly opposed the AC current system which made his DC current less relevant. In order to demonstrate the dangers of AC current, on January 4, 1903 he filmed the electrocution of an elephant named Topsy.

See also
Faradays Laws Motional EMF
Further reading
Matter and Interactions
External links
References
https://en.wikipedia.org/wiki/Electric_generator http://www.electrical4u.com/principle-of-dc-generator/ https://www.webassign.net/ebooks/mi4/toc.html?page=23.1 http://ethw.org/Generators