Gravitational waves: Difference between revisions
No edit summary |
No edit summary |
||
| (38 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
Gravitational waves are waves in the curvature of space-time believed to be emanating from gravity wells. | Gravitational waves are waves in the curvature of space-time believed to be emanating from gravity wells. They have now been directly observed. The gradual decay in angular momentum over the course of time in a orbital system can be attributed to the emission of gravitational waves. | ||
[[File:Graviational waves.jpg|thumb|While gravitational waves emit no light, here they can be visualized traveling through space-time.]] | |||
==Overview== | |||
Albert Einstein explained gravity in his theory of general relativity as a phenomenon resulting from the curvature of space-time. This curvature is caused by a mass distorting and bending the space-time in its sphere of influence. The gravitational waves radiate outward from the gravity well, and travel at the speed of light. These waves occur through the fabric of space-time much like mechanical waves travel through a fluid. As a gravitational wave passes an observer, it slightly alters the distance between the observer and the mass of origin by a factor of billionths of a millimeter. | |||
In order to understand this theory, think about a two-dimensional field, such as the ocean's surface. As a small speedboat travels across the water, it distorts the surface, causing ripples to travel perpendicular to its momentum. A larger ship would produce stronger waves, which would carry more energy. Gravitational waves are the three-dimensional counterpart to this analogy. The speedboat represents a planet, and the ship represents a star. The object of greater mass produces stronger gravitational waves. If the propulsion of the ship suddenly shut down, the ship would gradually slow down until its velocity was zero, due to the energy transfer from the movement of the ship to the water. As a planet or star moves through space, it too is slowing down due to the energy transfer to space-time in the form of gravitational waves. | |||
==History== | |||
Albert Einstein first theorized about gravitational waves in his Theory of General Relativity. He hypthesized that as a gravity well moves through space-time, it would emit a "wake," of energy much like a boat leaves a wake behind it in the water. | |||
In 1993, the Nobel Prize in Physics was awarded for the observations of the Hulse-Taylor star system, which provided some concrete evidence for the existence of gravitational waves. Observations made included the rate of change in the orbits of the two stars as they underwent orbital decay. | |||
On December 3, 2015, the European Space Agency launched a test probe, named LISA, designed to orbit at the L1 Lagrange Point and measure gravitational waves by measuring the relative positions of released gold-platinum cubes with high precision lasers. If gravitational waves do exist, then the the positions of the cubes should be several billionths of a millimeter off from free fall. | |||
==Mathematics== | |||
===Radiated Power=== | |||
The loss in energy from a system due to the radiation of gravitational waves can be predicted by using the following equation: | |||
:<math>P = \frac{\mathrm{d}E}{\mathrm{d}t} = - \frac{32}{5}\, \frac{G^4}{c^5}\, \frac{(m_1m_2)^2 (m_1+m_2)}{r^5}</math>, | |||
where E stands for Energy, and r represents the distance between the two objects. | |||
This radiated energy helps explain orbital decay, which is when two the orbit of one mass around another circularizes and the distance between them slowly begins to decrease. Earth is currently undergoing this phenomenon with the Sun, as it looses about 200 joules of total energy in its orbit every second. However, that only causes a decay of the orbit of only about 1E-15 meters per day. At that rate, it would take about 1E10 times the current age of the universe to fall into the Sun. | |||
===Orbital Decay=== | |||
As mentioned earlier, graviational radiation in the form of waves causes a system of two orbiting bodies to lose some energy, leading to orbital decay. For example, the system of a comet in a highly elliptical orbit and the Sun has some angular momentum, L. As gravitational waves are emanating from the center of mass from this system, the total energy of the system decreases, leading to a loss of angular momentum. Over time, this loss of energy causes the orbit of the comet to circularize, or become less elliptical. | |||
This orbital decay is also dependent on the mass of the two systems. The equation used to find the rate of change of the distance between two object due to the result of emanating gravitational waves is the following: | |||
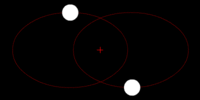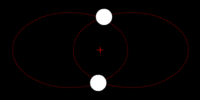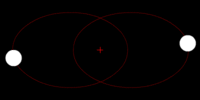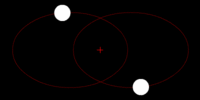
[[Image:orbit5.gif|thumb|200px|Two stars start out in highly elliptical orbits.]] | |||
[[Image:orbit1.gif|thumb|200px|The two stars' orbits now have decayed to the point where they are one and the same around their common center of mass.]] | |||
:<math>\frac{\mathrm{d}r}{\mathrm{d}t} = - \frac{64}{5}\, \frac{G^3}{c^5}\, \frac{(m_1m_2)(m_1+m_2)}{r^3}\ </math>, | |||
with the variables representing the same values as the previous equation. | |||
===A Computational Model=== | |||
Here we see the same system of two stars in a binary star system. Both start out in elliptical orbits around their commend center of mass. After quite a bit of time, their orbits will decay and circularize. After even more time, the two stars will eventually merge at the center of mass. | |||
== | ==Connectedness== | ||
How objects move through space has always fascinated me, especially due to the scale and the speed of celestial objects. As an Aerospace Engineering Major, I am much more interested in how we can learn about propulsion and energy just by observing the interactions of objects in the cosmos. By learning more about space-time, we could potentially develop methods of propelling our machines deeper into space than we previously thought possible. NASA and the ESA have already put extensive resources into studying gravitational waves in hopes that by unlocking their secrets, we could learn how to harness their power into future engineering projects. | |||
== See also == | == See also == | ||
===Further reading=== | ===Further reading=== | ||
=== | [http://www.nature.com/news/all-you-need-to-know-about-gravitational-waves-1.14886 "All You Need to Know About Gravitational Waves : Nature News & Comment." Nature News & Comment. N.p., n.d. Web. 5 Dec. 2015.] | ||
[http://m.esa.int/Our_Activities/Space_Science/LISA_Pathfinder_en_route_to_gravitational_wave_demonstration "LISA Pathfinder En Route to Gravitational Wave Demonstration / Space Science / Our Activities / ESA Mobile." European Space Agency. N.p., n.d. Web. 5 Dec. 2015.] | |||
===Also on PhysicsBook=== | |||
[http://www.physicsbook.gatech.edu/Einstein%27s_Theory_of_General_Relativity Einstein's Theory of General Relativity] | |||
[http://www.physicsbook.gatech.edu/Albert_Einstein Albert Einstein] | |||
[http://www.physicsbook.gatech.edu/Gravitational_Potential_Energy Gravitational Potential Energy] | |||
==References== | ==References== | ||
DISCLAIMER: ALL IMAGES AND GIFS WERE TAKEN FROM THE PUBLIC DOMAIN FOR THIS PAGE. I DO NOT OWN ANY OF THE CONTENT. | |||
All You Need to Know About Gravitational Waves : Nature News & Comment. (n.d.). Retrieved December 5, 2015, | |||
Gravitational waves and where to find them | symmetry magazine. (n.d.). Retrieved from [http://www.symmetrymagazine.org/article/gravitational-waves-and-where-to-find-them] | |||
[ | Gravitational Waves in General Relativity. VII. Waves from Axi-Symmetric Isolated Systems | Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences. (n.d.). Retrieved from [http://rspa.royalsocietypublishing.org/content/269/1336/21.short] | ||
Latest revision as of 12:45, 17 April 2016
Gravitational waves are waves in the curvature of space-time believed to be emanating from gravity wells. They have now been directly observed. The gradual decay in angular momentum over the course of time in a orbital system can be attributed to the emission of gravitational waves.
Overview
Albert Einstein explained gravity in his theory of general relativity as a phenomenon resulting from the curvature of space-time. This curvature is caused by a mass distorting and bending the space-time in its sphere of influence. The gravitational waves radiate outward from the gravity well, and travel at the speed of light. These waves occur through the fabric of space-time much like mechanical waves travel through a fluid. As a gravitational wave passes an observer, it slightly alters the distance between the observer and the mass of origin by a factor of billionths of a millimeter.
In order to understand this theory, think about a two-dimensional field, such as the ocean's surface. As a small speedboat travels across the water, it distorts the surface, causing ripples to travel perpendicular to its momentum. A larger ship would produce stronger waves, which would carry more energy. Gravitational waves are the three-dimensional counterpart to this analogy. The speedboat represents a planet, and the ship represents a star. The object of greater mass produces stronger gravitational waves. If the propulsion of the ship suddenly shut down, the ship would gradually slow down until its velocity was zero, due to the energy transfer from the movement of the ship to the water. As a planet or star moves through space, it too is slowing down due to the energy transfer to space-time in the form of gravitational waves.
History
Albert Einstein first theorized about gravitational waves in his Theory of General Relativity. He hypthesized that as a gravity well moves through space-time, it would emit a "wake," of energy much like a boat leaves a wake behind it in the water.
In 1993, the Nobel Prize in Physics was awarded for the observations of the Hulse-Taylor star system, which provided some concrete evidence for the existence of gravitational waves. Observations made included the rate of change in the orbits of the two stars as they underwent orbital decay.
On December 3, 2015, the European Space Agency launched a test probe, named LISA, designed to orbit at the L1 Lagrange Point and measure gravitational waves by measuring the relative positions of released gold-platinum cubes with high precision lasers. If gravitational waves do exist, then the the positions of the cubes should be several billionths of a millimeter off from free fall.
Mathematics
Radiated Power
The loss in energy from a system due to the radiation of gravitational waves can be predicted by using the following equation:
- [math]\displaystyle{ P = \frac{\mathrm{d}E}{\mathrm{d}t} = - \frac{32}{5}\, \frac{G^4}{c^5}\, \frac{(m_1m_2)^2 (m_1+m_2)}{r^5} }[/math],
where E stands for Energy, and r represents the distance between the two objects.
This radiated energy helps explain orbital decay, which is when two the orbit of one mass around another circularizes and the distance between them slowly begins to decrease. Earth is currently undergoing this phenomenon with the Sun, as it looses about 200 joules of total energy in its orbit every second. However, that only causes a decay of the orbit of only about 1E-15 meters per day. At that rate, it would take about 1E10 times the current age of the universe to fall into the Sun.
Orbital Decay
As mentioned earlier, graviational radiation in the form of waves causes a system of two orbiting bodies to lose some energy, leading to orbital decay. For example, the system of a comet in a highly elliptical orbit and the Sun has some angular momentum, L. As gravitational waves are emanating from the center of mass from this system, the total energy of the system decreases, leading to a loss of angular momentum. Over time, this loss of energy causes the orbit of the comet to circularize, or become less elliptical.
This orbital decay is also dependent on the mass of the two systems. The equation used to find the rate of change of the distance between two object due to the result of emanating gravitational waves is the following:
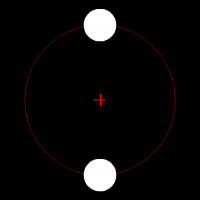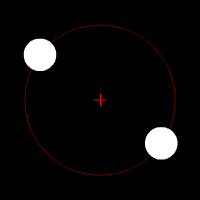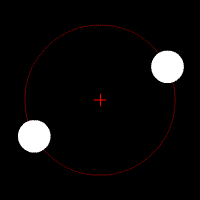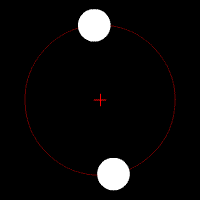
- [math]\displaystyle{ \frac{\mathrm{d}r}{\mathrm{d}t} = - \frac{64}{5}\, \frac{G^3}{c^5}\, \frac{(m_1m_2)(m_1+m_2)}{r^3}\ }[/math],
with the variables representing the same values as the previous equation.
A Computational Model
Here we see the same system of two stars in a binary star system. Both start out in elliptical orbits around their commend center of mass. After quite a bit of time, their orbits will decay and circularize. After even more time, the two stars will eventually merge at the center of mass.
Connectedness
How objects move through space has always fascinated me, especially due to the scale and the speed of celestial objects. As an Aerospace Engineering Major, I am much more interested in how we can learn about propulsion and energy just by observing the interactions of objects in the cosmos. By learning more about space-time, we could potentially develop methods of propelling our machines deeper into space than we previously thought possible. NASA and the ESA have already put extensive resources into studying gravitational waves in hopes that by unlocking their secrets, we could learn how to harness their power into future engineering projects.
See also
Further reading
Also on PhysicsBook
Einstein's Theory of General Relativity
Gravitational Potential Energy
References
DISCLAIMER: ALL IMAGES AND GIFS WERE TAKEN FROM THE PUBLIC DOMAIN FOR THIS PAGE. I DO NOT OWN ANY OF THE CONTENT.
All You Need to Know About Gravitational Waves : Nature News & Comment. (n.d.). Retrieved December 5, 2015,
Gravitational waves and where to find them | symmetry magazine. (n.d.). Retrieved from [1]
Gravitational Waves in General Relativity. VII. Waves from Axi-Symmetric Isolated Systems | Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences. (n.d.). Retrieved from [2]