Electric Polarization: Difference between revisions
Cthompson361 (talk | contribs) |
|||
| (107 intermediate revisions by 7 users not shown) | |||
| Line 1: | Line 1: | ||
Claimed by | '''''Claimed by Conner Thompson (Fall 2025)''''' | ||
== The Main Idea == | '''== The Main Idea == | ||
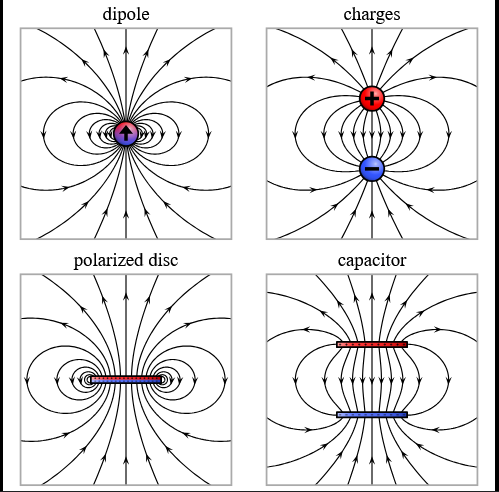
Polarization, used broadly, is the act of dividing into opposites. Electric polarization is the process of separating opposite charges inside an object. This occurs when an electric field, let's say created by a charged object A, induces the electrons to move in object B. This electron movement causes one portion of object B to have an excess negative charge and the other to have an excess positive charge. Object B could be a neutral object with a net charge of zero, but can still be polarized and attracted to object A. If A were positively charged, the electrons in object B would be attracted to the side closest to A (since opposite charges attract) which would create an induced dipole. This dipole is not permanent; if object A were to be removed, B would return to its neutral state. | |||
[[File:Phys.jpg]] [[File:dipoles.png]] | |||
Polarization is a different | === Cause of Polarization === | ||
The cause of polarization can be found when the structure of an atom is closely examined. Atoms have a positively charged nucleus consisting of protons and neutrons tightly clumped together. Surrounding this nucleus is a negatively charged electron cloud which is not rigidly connected to the nucleus. Since the negative electron cloud does not have to be centered at its corresponding positive nucleus, if an electric field is applied on the atom, the two opposite charges can move relative to one another. This applied electric field induced the polarization of atoms. | |||
We can see this exemplified when we look at a hydrogen atom for instance. From a microscopic perspective, it is hard to observe a single electron during polarization so we can look at an atom's electric cloud as a whole. When a positive charge was applied to a hydrogen atom, the electron cloud as shifted to the left due to the attraction to the opposite charge, while the atom's nucleus also shifted to the right. If we were observing a single electron, there is a greater chance that a single electron will be found to the right of the nucleus as opposed to the left. | |||
=== Types of Polarization === | |||
There are three main types of electric polarization: | |||
1. Electronic Polarization | |||
Occurs when an external electric field displaces the electron cloud relative to the nucleus. This happens in all atoms. | |||
2. Ionic Polarization | |||
Occurs in materials with positive and negative ions (like NaCl), where the ions shift relative to each other under an applied field. | |||
3. Orientation Polarization | |||
Occurs in polar molecules (such as water) when permanent dipoles rotate to align with the applied field. | |||
Each type has different time responses and dominates depending on the material and temperature. | |||
=== Computational Model === | |||
[https://trinket.io/glowscript/53eeede7fd0d This link shows a GlowScript computational model] that visualizes the following: | |||
1. External Electric Field | |||
Created by two capacitor plates (blue = negative, red = positive) | |||
2. Neutral Atoms in a Dielectric | |||
Each atom consists of: | |||
- A red nucleus | |||
- A cyan electron cloud | |||
3. Polarization | |||
When the user presses 'p', the electric field toggles ON/OFF: | |||
- Electron clouds shift opposite the field direction | |||
- Atoms become induced dipoles | |||
- The dielectric shows polarization alignment | |||
=== Conductors and Insulators === | |||
'''Conductors''' are materials that allow charged particles to move through/around it since it contains freely moving charged particles. One common conductor is an ionic solution, where there are charged particles dissolved in solution. These charged particles can freely move around the solution. When an external electric field is applied to the solution, negative particles will move against the direction of the electric field while positively charges particles move along the same direction. Another common conductor are metals. The atoms in metal are arranged in a lattice structure, where electrons can move freely inbetween atoms around the metal. This can be visualized as a 'sea' of mobile electrons. electrons are transferred across the surface of the object and it becomes polarized. | |||
'''Insulators''' are materials that do not conduct very much electric charge because all the electrons are rigidly bound to the atoms or molecules; they do not permit the free flow of electrons. When an insulator is subjected to an electric field, individual atoms or molecules are polarized rather than the whole object. Given this property, polarization in insulators happens very rapidly, in a matter of nanoseconds. The electric dipole moments of each individual polarized atom are all pointed in the same direction and sum to form a net electric field due to polarization(Epol) that can counteract on the applied field. In contrast to conductors, which have their excess charges on the surface, all of the excess charges in an insulator stay in the interior. | |||
The distinguishing feature of conductors that makes them susceptible to polarization is that that conductors have moving charges. This property is especially predominant in metals, where there is a "sea" of mobile electrons. Because charges move around in conductors, we can measure their speed through ''drift speed''. | |||
'''Drift speed: V=uE''' | |||
Where | |||
''V'' is drift speed, | |||
''u'' is mobility of the charge, | |||
and ''E'' is the magnitude of the electric field, | |||
When a conductor is at equilibrium, the drift speed will reach 0. This is because when charges move to different sides, they begin to create an electric field between them that counteracts the applied field. As the charges move further apart, the magnitude of Epol gets closer to the magnitude of the applied field. Once they equal each other, the net electric field on the charged particles is 0, therefore their drift speed is also 0. Inside metals, where the excess charges reside on the surface, the net electric field inside the metal is 0 everywhere at equilibrium due to the addition of the applied field and polarized electric field. | |||
An example of a polarized insulator: | |||
[[File:Screen_Shot_2016-11-27_at_10.52.28_PM.png]] | |||
=== Common Misconception === | |||
Neutral objects (with a net charge of zero) CAN be attracted to charged ones because induced dipoles are formed and create an electric field at the location of the object. However, repulsion of an induced object cannot happen as it always brings unlike signs closer. | |||
=== Mathematical Model === | |||
The amount of induced polarization is directly proportional to the magnitude of the applied electric field. | |||
Induced Polarization : <math>\vec{P} = \alpha \vec{E}</math> . | |||
'''"P"''' is the dipole moment of polarized atoms, '''"α"''' is the polarizability of a particular material, and '''"E"''' is the applied electric field. The value of '''"α"''' is dependent on many factors, has been recorded through experiments, and can be obtained through reference manuals. | |||
The dipole moment can also be related to the distance of separation caused by polarization and the charge. | |||
<math>\vec{P} = qs</math> | |||
Applied electric field from a point charge is equal to: | |||
[[File:Electricfieldet.jpg]] | |||
== Examples == | == Examples == | ||
==='''Simple'''=== | |||
===== -Question ===== | |||
A positively charged object is placed near a neutral atom. Draw the polarization of the atom. | |||
[[File:PolarizationQ1.png|750px]] | |||
===== -Answer ===== | |||
The positive point charge created an electric field point outward in all directions from the point. The net electric field on the neutral atom points to the right. This external applied electric field produces a force on the charged particles in the atom. The electric force is determined by the product of the electric field and the charge of the affected object (F = qE). The positive nucleus experiences a force away from the point charge while the electron cloud experiences a force towards the point charge due to its negative charge. This results in a net shift of the electron cloud towards the point charge to polarize the atom. However, don't think that the electron cloud is stripped from nucleus! The electrons are strongly attracted to the nucleus and the net shift is incredibly small, but enough to create a dipole moment. | |||
[[File:PolarizationA1.png|750px]] | |||
Simpler Model: | |||
[[File:etpolarizedatom.png]] | |||
==='''Middling'''=== | |||
===== -Question ===== | |||
A negatively charged object is placed to the right of a metal sphere in equilibrium. Draw the polarization of the sphere. | |||
[[File:PolarizationQ2.png]] | |||
===== -Answer ===== | |||
The external applied electric field on the metal by the negatively charged object creates an electric force on the charged particles of the metal. One key difference is that electrons(specifically outer/valence) are able to move freely in a lattice structure within the metal sphere while the nuclei of the metal atoms are more bound to their position. The electric force causes the entire "sea" of electrons in the metal to shift right towards the object, causing the metal to polarize with a negatively charged surface on the right and a positively charged surface on the left. At some point the metal will reach equilibrium, where the magnitude of the applied electric field will be equal to the electric field created inside the metal due to the polarization and the metal will polarize no more. Interestingly, these conditions result in a net electric field of 0 inside the metal. | |||
[[File:PolarizationA2.png]] | |||
==='''Difficult'''=== | |||
===== -Question ===== | |||
A negatively charged metal object is placed in a region with an electric field going in the +y direction. Draw the polarization of the object. | |||
[[File:DifficultQuestion.png]] | |||
===== -Answer ===== | |||
Since the metal already has a excess of negative charge, the polarization will be a little different. The applied field will cause electrons to shift down. The accumulation of electrons on the bottom side starts creating a growing electric field in the opposite direction of the applied field, and repels incoming electrons. Electrons move until the net electric field is 0(equilibrium). Since the metal had an initial negative charge, the charges repel each other to the surface, with more electrons towards the bottom surface. There is no excess positive charge anywhere. | |||
[[File:DifficultAnswer.png]] | |||
[[File:etmetalblock.png]] | |||
== Connectedness == | == Connectedness == | ||
Electric polarization is a key component of insulators and conductors. These materials and their uses are incredibly important for every day life. For example, lightbulb filaments are conductors which carry electrons from a negatively charged area to a positively charged area. Insulators, which don't conduct electric charges, can be used to insulate buildings. This is related to my major of study, environmental engineering, because we work to make buildings more sustainable by reducing the amount of energy required to keep them running. | |||
While there is no direct correlation of electric polarization to my major (industrial engineering), there is one indirect parallel. By looking at the history of electric polarization, and how the understanding we have came to be, we can infer that the concept went through several iterations before it became widely accepted. In that same vein, many theorems and principles in stochastics, optimization, and simulations similarly were expounded on over the years before they were accepted into practice. | |||
Interestingly, the effects of polarization of particles can even be applied to my major in Neuroscience. The nerves in our body send electrical signals by mechanically separating charged particles such as Na+,K+, and Cl-. This separation results in a electric field due to polarization(Epol) which contributes to the force to drive these particles back and allow for a quicker depolarization when a electrical signal must be sent. | |||
== History == | == History == | ||
Benjamin Franklin was the first person to use "positive" and "negative" in describing charges and came up with principle of conservation of charges. In 1897, J.J. Thomson experimented with cathode rays and found out that electrons exist in the rays. In 1911, Ernest Rutherford discovered that atoms have a concentrated positive center with protons fixed inside nucleus. | |||
Experimental studies in the 18th century made it possible to distinguish positive and negative charges. The properties of charges in a condenser were studied and reported by Faraday in 1837, which he called the dielectric. He also introduced the concept of permittivity/dielectric constant, which is represented by ε. Simultaneously, Maxwell presented this theory of electromagnetic phenomena, which tied electric field intensity and dielectric displacement. | |||
In the 19th century, Debye published a theory that extended the Clausius-Mossotti equation, which consequently came to be known as the Debye equation. This equation shed light upon the fact that the dielectric constant depended on both molecular polarizability as well as the permanent moment of the molecules. | |||
In 1936, Onsager modified Debye's work and found that Debye had included torque in his calculations when he shouldn't have. Onsager furthered the relation of the dilelectric constant and the molecular dipole moment by describing their relationship in polar liquids and non-polar solvents. | |||
== See Also == | == See Also == | ||
*[[Charge]] | |||
*[[Electric Field]] | |||
*[[Benjamin Franklin]] | |||
*[[J.J. Thomson]] | |||
*[[Ernest Rutherford]] | |||
=== Further Reading === | === Further Reading === | ||
Physics of Dielectrics for the Engineer by Roland Coelho | |||
==== Application ==== | |||
http://www.nrcresearchpress.com/doi/abs/10.1139/t89-067?journalCode=cgj#.VmFE97mFPIU | http://www.nrcresearchpress.com/doi/abs/10.1139/t89-067?journalCode=cgj#.VmFE97mFPIU | ||
=== External Links === | === External Links === | ||
| Line 37: | Line 162: | ||
http://www.physicsclassroom.com/class/estatics/Lesson-1/Polarization | http://www.physicsclassroom.com/class/estatics/Lesson-1/Polarization | ||
https://www. | https://www.youtube.com/watch?v=3xSIA5UVAo8 | ||
http://scienceline.ucsb.edu/getkey.php?key=408 | |||
https://www.aip.org/history/gap/Franklin/Franklin.html | |||
https://www.youtube.com/watch?v=HKgOpmX-OFI | |||
https://www.britannica.com/science/electric-polarization | |||
https://www.youtube.com/watch?v=2KTGdX951Z0 | |||
Matter and Interactions Fourth Edition by Ruth W. Chabay, Bruce A. Sherwood | Matter and Interactions Fourth Edition by Ruth W. Chabay, Bruce A. Sherwood | ||
Latest revision as of 23:57, 23 November 2025
Claimed by Conner Thompson (Fall 2025)
== The Main Idea ==
Polarization, used broadly, is the act of dividing into opposites. Electric polarization is the process of separating opposite charges inside an object. This occurs when an electric field, let's say created by a charged object A, induces the electrons to move in object B. This electron movement causes one portion of object B to have an excess negative charge and the other to have an excess positive charge. Object B could be a neutral object with a net charge of zero, but can still be polarized and attracted to object A. If A were positively charged, the electrons in object B would be attracted to the side closest to A (since opposite charges attract) which would create an induced dipole. This dipole is not permanent; if object A were to be removed, B would return to its neutral state.
Cause of Polarization
The cause of polarization can be found when the structure of an atom is closely examined. Atoms have a positively charged nucleus consisting of protons and neutrons tightly clumped together. Surrounding this nucleus is a negatively charged electron cloud which is not rigidly connected to the nucleus. Since the negative electron cloud does not have to be centered at its corresponding positive nucleus, if an electric field is applied on the atom, the two opposite charges can move relative to one another. This applied electric field induced the polarization of atoms.
We can see this exemplified when we look at a hydrogen atom for instance. From a microscopic perspective, it is hard to observe a single electron during polarization so we can look at an atom's electric cloud as a whole. When a positive charge was applied to a hydrogen atom, the electron cloud as shifted to the left due to the attraction to the opposite charge, while the atom's nucleus also shifted to the right. If we were observing a single electron, there is a greater chance that a single electron will be found to the right of the nucleus as opposed to the left.
Types of Polarization
There are three main types of electric polarization:
1. Electronic Polarization
Occurs when an external electric field displaces the electron cloud relative to the nucleus. This happens in all atoms.
2. Ionic Polarization
Occurs in materials with positive and negative ions (like NaCl), where the ions shift relative to each other under an applied field.
3. Orientation Polarization
Occurs in polar molecules (such as water) when permanent dipoles rotate to align with the applied field.
Each type has different time responses and dominates depending on the material and temperature.
Computational Model
This link shows a GlowScript computational model that visualizes the following:
1. External Electric Field
Created by two capacitor plates (blue = negative, red = positive)
2. Neutral Atoms in a Dielectric
Each atom consists of: - A red nucleus - A cyan electron cloud
3. Polarization
When the user presses 'p', the electric field toggles ON/OFF: - Electron clouds shift opposite the field direction - Atoms become induced dipoles - The dielectric shows polarization alignment
Conductors and Insulators
Conductors are materials that allow charged particles to move through/around it since it contains freely moving charged particles. One common conductor is an ionic solution, where there are charged particles dissolved in solution. These charged particles can freely move around the solution. When an external electric field is applied to the solution, negative particles will move against the direction of the electric field while positively charges particles move along the same direction. Another common conductor are metals. The atoms in metal are arranged in a lattice structure, where electrons can move freely inbetween atoms around the metal. This can be visualized as a 'sea' of mobile electrons. electrons are transferred across the surface of the object and it becomes polarized.
Insulators are materials that do not conduct very much electric charge because all the electrons are rigidly bound to the atoms or molecules; they do not permit the free flow of electrons. When an insulator is subjected to an electric field, individual atoms or molecules are polarized rather than the whole object. Given this property, polarization in insulators happens very rapidly, in a matter of nanoseconds. The electric dipole moments of each individual polarized atom are all pointed in the same direction and sum to form a net electric field due to polarization(Epol) that can counteract on the applied field. In contrast to conductors, which have their excess charges on the surface, all of the excess charges in an insulator stay in the interior.
The distinguishing feature of conductors that makes them susceptible to polarization is that that conductors have moving charges. This property is especially predominant in metals, where there is a "sea" of mobile electrons. Because charges move around in conductors, we can measure their speed through drift speed.
Drift speed: V=uE
Where V is drift speed, u is mobility of the charge, and E is the magnitude of the electric field,
When a conductor is at equilibrium, the drift speed will reach 0. This is because when charges move to different sides, they begin to create an electric field between them that counteracts the applied field. As the charges move further apart, the magnitude of Epol gets closer to the magnitude of the applied field. Once they equal each other, the net electric field on the charged particles is 0, therefore their drift speed is also 0. Inside metals, where the excess charges reside on the surface, the net electric field inside the metal is 0 everywhere at equilibrium due to the addition of the applied field and polarized electric field.
An example of a polarized insulator:
Common Misconception
Neutral objects (with a net charge of zero) CAN be attracted to charged ones because induced dipoles are formed and create an electric field at the location of the object. However, repulsion of an induced object cannot happen as it always brings unlike signs closer.
Mathematical Model
The amount of induced polarization is directly proportional to the magnitude of the applied electric field.
Induced Polarization : [math]\displaystyle{ \vec{P} = \alpha \vec{E} }[/math] . "P" is the dipole moment of polarized atoms, "α" is the polarizability of a particular material, and "E" is the applied electric field. The value of "α" is dependent on many factors, has been recorded through experiments, and can be obtained through reference manuals.
The dipole moment can also be related to the distance of separation caused by polarization and the charge. [math]\displaystyle{ \vec{P} = qs }[/math]
Applied electric field from a point charge is equal to:

Examples
Simple
-Question
A positively charged object is placed near a neutral atom. Draw the polarization of the atom.
-Answer
The positive point charge created an electric field point outward in all directions from the point. The net electric field on the neutral atom points to the right. This external applied electric field produces a force on the charged particles in the atom. The electric force is determined by the product of the electric field and the charge of the affected object (F = qE). The positive nucleus experiences a force away from the point charge while the electron cloud experiences a force towards the point charge due to its negative charge. This results in a net shift of the electron cloud towards the point charge to polarize the atom. However, don't think that the electron cloud is stripped from nucleus! The electrons are strongly attracted to the nucleus and the net shift is incredibly small, but enough to create a dipole moment.
Simpler Model:
Middling
-Question
A negatively charged object is placed to the right of a metal sphere in equilibrium. Draw the polarization of the sphere.
-Answer
The external applied electric field on the metal by the negatively charged object creates an electric force on the charged particles of the metal. One key difference is that electrons(specifically outer/valence) are able to move freely in a lattice structure within the metal sphere while the nuclei of the metal atoms are more bound to their position. The electric force causes the entire "sea" of electrons in the metal to shift right towards the object, causing the metal to polarize with a negatively charged surface on the right and a positively charged surface on the left. At some point the metal will reach equilibrium, where the magnitude of the applied electric field will be equal to the electric field created inside the metal due to the polarization and the metal will polarize no more. Interestingly, these conditions result in a net electric field of 0 inside the metal.
Difficult
-Question
A negatively charged metal object is placed in a region with an electric field going in the +y direction. Draw the polarization of the object.

-Answer
Since the metal already has a excess of negative charge, the polarization will be a little different. The applied field will cause electrons to shift down. The accumulation of electrons on the bottom side starts creating a growing electric field in the opposite direction of the applied field, and repels incoming electrons. Electrons move until the net electric field is 0(equilibrium). Since the metal had an initial negative charge, the charges repel each other to the surface, with more electrons towards the bottom surface. There is no excess positive charge anywhere.
Connectedness
Electric polarization is a key component of insulators and conductors. These materials and their uses are incredibly important for every day life. For example, lightbulb filaments are conductors which carry electrons from a negatively charged area to a positively charged area. Insulators, which don't conduct electric charges, can be used to insulate buildings. This is related to my major of study, environmental engineering, because we work to make buildings more sustainable by reducing the amount of energy required to keep them running.
While there is no direct correlation of electric polarization to my major (industrial engineering), there is one indirect parallel. By looking at the history of electric polarization, and how the understanding we have came to be, we can infer that the concept went through several iterations before it became widely accepted. In that same vein, many theorems and principles in stochastics, optimization, and simulations similarly were expounded on over the years before they were accepted into practice.
Interestingly, the effects of polarization of particles can even be applied to my major in Neuroscience. The nerves in our body send electrical signals by mechanically separating charged particles such as Na+,K+, and Cl-. This separation results in a electric field due to polarization(Epol) which contributes to the force to drive these particles back and allow for a quicker depolarization when a electrical signal must be sent.
History
Benjamin Franklin was the first person to use "positive" and "negative" in describing charges and came up with principle of conservation of charges. In 1897, J.J. Thomson experimented with cathode rays and found out that electrons exist in the rays. In 1911, Ernest Rutherford discovered that atoms have a concentrated positive center with protons fixed inside nucleus.
Experimental studies in the 18th century made it possible to distinguish positive and negative charges. The properties of charges in a condenser were studied and reported by Faraday in 1837, which he called the dielectric. He also introduced the concept of permittivity/dielectric constant, which is represented by ε. Simultaneously, Maxwell presented this theory of electromagnetic phenomena, which tied electric field intensity and dielectric displacement.
In the 19th century, Debye published a theory that extended the Clausius-Mossotti equation, which consequently came to be known as the Debye equation. This equation shed light upon the fact that the dielectric constant depended on both molecular polarizability as well as the permanent moment of the molecules.
In 1936, Onsager modified Debye's work and found that Debye had included torque in his calculations when he shouldn't have. Onsager furthered the relation of the dilelectric constant and the molecular dipole moment by describing their relationship in polar liquids and non-polar solvents.
See Also
Further Reading
Physics of Dielectrics for the Engineer by Roland Coelho
Application
http://www.nrcresearchpress.com/doi/abs/10.1139/t89-067?journalCode=cgj#.VmFE97mFPIU
External Links
https://courses.cit.cornell.edu/ece303/Lectures/lecture7.pdf
Reference
http://www.physicsclassroom.com/class/estatics/Lesson-1/Polarization
https://www.youtube.com/watch?v=3xSIA5UVAo8
http://scienceline.ucsb.edu/getkey.php?key=408
https://www.aip.org/history/gap/Franklin/Franklin.html
https://www.youtube.com/watch?v=HKgOpmX-OFI
https://www.britannica.com/science/electric-polarization
https://www.youtube.com/watch?v=2KTGdX951Z0
Matter and Interactions Fourth Edition by Ruth W. Chabay, Bruce A. Sherwood