Law of Gravitation: Difference between revisions
No edit summary |
No edit summary |
||
| (21 intermediate revisions by the same user not shown) | |||
| Line 22: | Line 22: | ||
==Two Mathematical Model== | ==Two Mathematical Model== | ||
Work In Progress by Sitong Wu: [[User:Swu321|Swu321]] ([[User talk:Swu321|talk]]) | |||
===(1) At any position inside a uniform shell, the gravitational force on an object is ZERO=== | ===(1) At any position inside a uniform shell, the gravitational force on an object is ZERO=== | ||
[[File:Bottomofcone.jpg|450px|thumb|right|]] As the figure 3.1 shows, a uniform spherical shell is equal to many thin spherical shell adding together. Randomly picking one of the thin shell which has mass M and a mass point m inside the shell, we can calculate the gravitational force on the mass point. We can draw two cones which has the same vertex point at position P, which is also the position of the mass point m. If the area of the bottoms of these two cones are small enough, though the bottom of these two cones are not flat and these two cones are not exact cones, we can treat these two cone-like shapes as cones. | [[File:Bottomofcone.jpg|450px|thumb|right|]] As the figure 3.1 shows, a uniform spherical shell is equal to many thin spherical shell adding together. Randomly picking one of the thin shell which has mass M and a mass point m inside the shell, we can calculate the gravitational force on the mass point. We can draw two cones which has the same vertex point at position P, which is also the position of the mass point m. If the area of the bottoms of these two cones are small enough, though the bottom of these two cones are not flat and these two cones are not exact cones, we can treat these two cone-like shapes as cones. | ||
| Line 34: | Line 35: | ||
These two force F1 and F2 have the same magnitude but opposite direction. So, the net force on the mass point is ZERO. Thus, inside the spherical shell, the net attraction force from any other pairs of position points are all ZERO. | These two force F1 and F2 have the same magnitude but opposite direction. So, the net force on the mass point is ZERO. Thus, inside the spherical shell, the net attraction force from any other pairs of position points are all ZERO. | ||
===(2) Inside a uniform solid sphere, there is a mass point which has the distance r from the center of the sphere. | ===(2) Inside a uniform solid sphere, there is a mass point which has the distance r from the center of the sphere. Then, the gravitational force on the mass point is <math>F=G*\frac{Mm}{r}</math>=== | ||
[[File:Shellinside.jpg |300px|thumb|right|]] | |||
<math> | As the figure 3.2 shows, assume the uniform spherical solid has mass M and radius R. Choose part of the solid which is a spherical solid that has radius r and has the same center as the larger solid. There is a mass point inside the larger solid which has distance r from the center, which means that mass point is on the smaller solid. The net gravitational force is the force from the spherical shell which has length (R-r) and the smaller spherical solid which has radius r. From part 1, we knows that the force from the shell is ZERO so that the gravitational force on the mass point is only contributed by the smaller spherical solid. | ||
<math>F=G*\frac{Mm}{r}</math> | |||
== | If it is known that the total mass of the spherical solid is M, then | ||
<math>\frac{M1}{M}=\frac{r^3}{R^3}</math> | |||
and | |||
<math>M1=\frac{M}{R^3}*r^3</math> | |||
== | then | ||
<math>F = G*\frac{M1*m}{r^2}=G*\frac{M*m}{R^3}*r</math> | |||
When r = 0, we have M1 = 0 and F = 0 | |||
When r = R, we have <math>F=G*\frac{M*m}{R^2}</math> | |||
== | |||
==History== | ==History== | ||
See External links | |||
== See also == | == See also == | ||
[https://en.wikipedia.org/wiki/Aerospace Aerospace] | |||
===Further reading=== | ===Further reading=== | ||
A Brief History of Time[http://www.amazon.com/s/ref=nb_sb_ss_c_0_12?url=search-alias%3Daps&field-keywords=a+brief+history+of+time&sprefix=a+brief+hist%2Caps%2C165] | |||
Relativity[http://www.amazon.com/s/ref=nb_sb_noss?url=search-alias%3Daps&field-keywords=relativeity&rh=i%3Aaps%2Ck%3Arelativeity] | |||
===External links=== | ===External links=== | ||
[ | [https://en.wikipedia.org/wiki/Newton%27s_law_of_universal_gravitation Newton's law of universal gravitation] | ||
[https://en.wikipedia.org/wiki/Force Force] | |||
[https://en.wikipedia.org/wiki/Johannes_Kepler Kepler] | |||
[https://en.wikipedia.org/wiki/Isaac_Newton Newton] | |||
[ | |||
Latest revision as of 16:43, 4 December 2015
Every two objects in nature attract each other. The magnitude of the attraction force is proportional to the product of the masses of these two objects, and inverse proportional to the square of the distance between these two objects. This page is about Kepler's Three Laws and Law of Gravitation.
Kepler's Three Laws
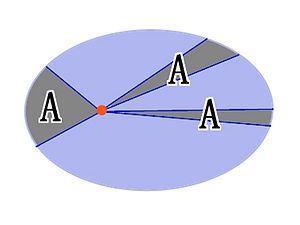
(1) Kepler's First Law
Kepler's First Law which is also called ellipse orbital law. This law talks about that all the planets that rotate around the sun has a orbital shape of ellipse. Sun is at one focal point of all the ellipse orbitals.
(2) Kepler's Second Law
Kepler's Second Law which is also called area law talks about that the line connected the planet and the sun will swipe the same area at the same period of time.
(3) Kepler's Third Law
Kepler's Third Law which is also called period law talks about that the ratio of cube of half of the length of the major axis to the square of the orbital period for every planet around the sun is the same. [math]\displaystyle{ \frac{R^3}{T^2}=k \text{ or }\frac{R1^3}{T1^2}=\frac{R2^3}{R2^2} }[/math] Note that Kepler's Third Law does not only work for planet but also work for satellite. The constant k is only related to the central celestial body.
Law of Gravitation
Every two objects in nature attract each other. The magnitude of the attraction force is proportional to the product of the masses of these two objects, and inverse proportional to the square of the distance between these two objects. If using m1 and m2 to represent the mass of two objects, and using r to represent the distance between these two objects, then the equation of Law of Gravitation is [math]\displaystyle{ F=G \frac{m1*m2}{r^2} }[/math] In this equation, the unit of mass is kg, the unit of distance is m, and the unit of force is N. G is a constant, which can be used for another objects. The magnitude of G is equal to the gravitational force between two 1 kg objects when they are separated by 1 m. The standard value of G is around 6.67259e-11 N*m^2/kg^2. Usually using 6.67e-11.
Two Mathematical Model
Work In Progress by Sitong Wu: Swu321 (talk)
(1) At any position inside a uniform shell, the gravitational force on an object is ZERO
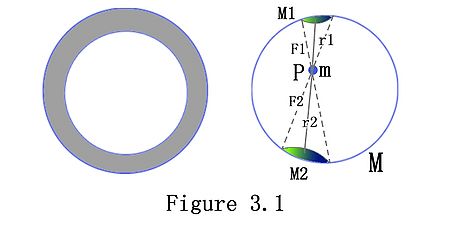
As the figure 3.1 shows, a uniform spherical shell is equal to many thin spherical shell adding together. Randomly picking one of the thin shell which has mass M and a mass point m inside the shell, we can calculate the gravitational force on the mass point. We can draw two cones which has the same vertex point at position P, which is also the position of the mass point m. If the area of the bottoms of these two cones are small enough, though the bottom of these two cones are not flat and these two cones are not exact cones, we can treat these two cone-like shapes as cones.
Assume that the distances from the bottoms of the cones are r1 and r2 respectively, radius of cones are R1 and R2, and the density of these two bottoms are ρ. Therefore, by the law of gravity, we can get the equations which represent the gravitational forces at the mass point from each of the bottoms. [math]\displaystyle{ F1 = G*\frac{M1M}{R1^2}=G*\frac{πR1^2*ρM}{R1^2} }[/math] [math]\displaystyle{ F2 = G*\frac{M2M}{R2^2}=G*\frac{πR2^2*ρM}{R2^2} }[/math] and by the rule of similar triangle, we can have [math]\displaystyle{ \frac{R1}{r1}=\frac{R2}{r2} }[/math] Therefore, the ratio of the gravitational force (attraction force) on the mass point from these two bottoms is [math]\displaystyle{ \frac{F1}{F2}=\frac{(R1/r1)^2}{(R2/r2)^2} }[/math]
These two force F1 and F2 have the same magnitude but opposite direction. So, the net force on the mass point is ZERO. Thus, inside the spherical shell, the net attraction force from any other pairs of position points are all ZERO.
(2) Inside a uniform solid sphere, there is a mass point which has the distance r from the center of the sphere. Then, the gravitational force on the mass point is [math]\displaystyle{ F=G*\frac{Mm}{r} }[/math]
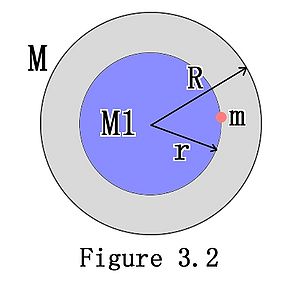
As the figure 3.2 shows, assume the uniform spherical solid has mass M and radius R. Choose part of the solid which is a spherical solid that has radius r and has the same center as the larger solid. There is a mass point inside the larger solid which has distance r from the center, which means that mass point is on the smaller solid. The net gravitational force is the force from the spherical shell which has length (R-r) and the smaller spherical solid which has radius r. From part 1, we knows that the force from the shell is ZERO so that the gravitational force on the mass point is only contributed by the smaller spherical solid. [math]\displaystyle{ F=G*\frac{Mm}{r} }[/math] If it is known that the total mass of the spherical solid is M, then [math]\displaystyle{ \frac{M1}{M}=\frac{r^3}{R^3} }[/math] and [math]\displaystyle{ M1=\frac{M}{R^3}*r^3 }[/math] then [math]\displaystyle{ F = G*\frac{M1*m}{r^2}=G*\frac{M*m}{R^3}*r }[/math] When r = 0, we have M1 = 0 and F = 0 When r = R, we have [math]\displaystyle{ F=G*\frac{M*m}{R^2} }[/math]
History
See External links
See also
Further reading
A Brief History of Time[1] Relativity[2]