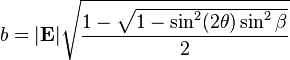Polarization of Waves: Difference between revisions
| (44 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
==The Main Idea== | ==The Main Idea== | ||
There are three main types of wave polarization. A wave is polarized when | [[File:Types of Polarization.gif|400px|thumb|right|Circular Polarization]] | ||
There are three main types of wave polarization. A wave is polarized when two electromagnetic waves are traveling co-linearly and the electric field components are perpendicular to each other. | |||
'''Linear Polarization''' | '''Linear Polarization'''[[File:Linear Polarization.gif|400px|thumb|right|Linear Polarization]] | ||
Most natural light is linearly polarized. The polarization shape is described by the electric field vector. In the case of a basic electromagnetic wave, as shown to the right, the electric field vector points up and down vertically as the wave travels. | Most natural light is linearly polarized. The polarization shape is described by the electric field vector. In the case of a basic electromagnetic wave, as shown to the right, the electric field vector points up and down vertically as the wave travels. | ||
'''Circular Polarization'''[[File:Circular Polarization.gif|400px|thumb|right|Circular Polarization]] | |||
Light which is polarized circularly consists of two perpendicular electromagnetic waves. In this case, show to the right, there are two electric fields which are perpendicular to each other (the illustration does not show the magnetic fields). These electric fields have equal amplitude but have a phase shift of 90 degrees. This creates an electric field vector which moves in a circle as the wave travels. | |||
[[File: | '''Elliptical Polarization'''[[File:Elliptical Polarization.gif|400px|thumb|right|Elliptical Polarization]] | ||
Elliptical polarization is very similar to circular polarization. In this case, shown to the right, the electric fields are still perpendicular and of the same amplitude. The difference is that the electric fields do not have equal amplitudes. Therefore the electric field vector creates an elliptical shape as the wave progresses - due to the changing magnitude and direction. | |||
== Mathematical Models== | |||
'''Linear Model''' | |||
[[File: | [[File:Linear_Equation.gif]] | ||
The linear model only consists of a single electric field wave. | |||
'''Circular Model''' | |||
[[File:Circular_Equation.gif]] | |||
The circular model consists of two components that are perpendicular, 90 degrees out of phase, and equal amplitude. | |||
'''Elliptical Model''' | |||
[[File:Elliptical_Equation.gif]] | |||
The elliptical model consists of two components that are perpendicular, 90 degrees out of phase, with different amplitude. | |||
==Examples== | ==Examples== | ||
===Determining Polarization=== | |||
Below are the equations for calculating the major and minor axes of the ellipse, a and b, respectively. | |||
(Note that Beta is the phase shift between wave components.) | |||
[[File:A_calculation.png]] | |||
[[File:B_calculation.png]] | |||
'''A) What shape does the electric field vector form when Beta = 0?''' | |||
:When Beta = 0 there exists no phase shift between waves. Therefore the wave is linearly polarized. | |||
== | '''B) What shape does the electric field vector form when a = b = E*root(2)?''' | ||
== | :When a is equal to b, the major and minor axes of the ellipse are equal. As a and b approach equality, the ellipse becomes a circle. Therefore the wave is circularly polarized. | ||
'''C) A wave consists of two components. Both are described by cosine functions with equal coefficients. The argument of the first cosine function is (wt-kz)''' | |||
:'''and the second is (wt-kz+pi/2). What shape does the electric field vector form?''' | |||
:If the cosine functions had the same argument then the shape would be linear (diagonal). In this case the second cosine function is shifted by pi/2 or 180 degrees. | |||
:As a result the two waves are shifted and have equal amplitude. Therefore the wave is circularly polarized. | |||
==Application== | |||
Electromagnetic polarization is a fundamental concept of light. Anything we see with our eyes is affected by the polarization of light. Most people are familiar with polarized sunglasses which reduce glare from reflected light, but there are many other applications. Three dimensional movie projections use polarized filters on two projectors and polarized glasses to show a single perspective to each eye. Polarized filters are also used to analyse stress in plastics. Shining light through filters and the plastic displays color bands describing the plastic's structure. The technology is also used in geology. Geologists use microscopes with polarized lenses which allow them to identify different types of materials. Polarization is used in analyzing cosmic radiation as well. Scientists use this information to study the early universe. | |||
==History== | ==History== | ||
The theory of electromagnetic waves was created in the 19th century as a result of knowledge of Electric and Magnetic fields. Scientists such as Faraday knew that magnetic fields created electric current and that electric currents produced magnetic fields. The idea behind EM waves was that electric fields and magnetic fields could alternate and propagate through space. The problem was that space had no medium for the wave to travel through. This problem was solved by James Clarke Maxwell when he proposed that electric current could travel through space if it did so at high speed. At this point Maxwell realized that this wave was light. Later, Heinrich Hertz learned that electric current in a wire could produce these EM waves. Since then, scientists have developed ways to produce and receive EM waves. This unlocked our understanding of the electromagnetic spectrum. | |||
== See also == | == See also == | ||
===Further reading=== | ===Further reading=== | ||
[[Electric Field]] | |||
[[Magnetic Field]] | |||
[[Electromagnetic Spectrum]] | |||
[[Transverse and Longitudinal Waves]] | |||
===External links=== | ===External links=== | ||
[https://www.youtube.com/watch?v=Q0qrU4nprB0 Animation] | |||
[https://en.wikipedia.org/wiki/Linear_polarization Linear Polarization] | |||
[https://en.wikipedia.org/wiki/Circular_polarization Circular Polarization] | |||
[https://en.wikipedia.org/wiki/Elliptical_polarization Elliptical Polarization] | |||
==References== | ==References== | ||
http://www.slideshare.net/pabitadhungel321/polarization-and-its-application | |||
https://en.wikipedia.org/wiki/Linear_polarization | |||
http://farside.ph.utexas.edu/teaching/315/Waves/node50.html | |||
http://hyperphysics.phy-astr.gsu.edu/hbase/phyopt/polclas.html | |||
Latest revision as of 20:08, 5 December 2015
The Main Idea

There are three main types of wave polarization. A wave is polarized when two electromagnetic waves are traveling co-linearly and the electric field components are perpendicular to each other.
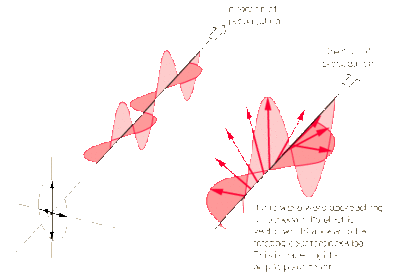
Linear Polarization
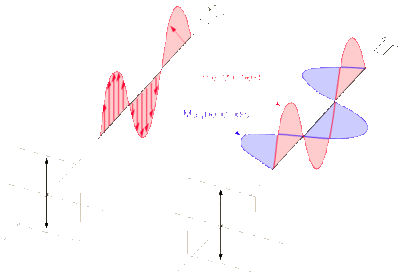
Most natural light is linearly polarized. The polarization shape is described by the electric field vector. In the case of a basic electromagnetic wave, as shown to the right, the electric field vector points up and down vertically as the wave travels.
Circular Polarization
Light which is polarized circularly consists of two perpendicular electromagnetic waves. In this case, show to the right, there are two electric fields which are perpendicular to each other (the illustration does not show the magnetic fields). These electric fields have equal amplitude but have a phase shift of 90 degrees. This creates an electric field vector which moves in a circle as the wave travels.
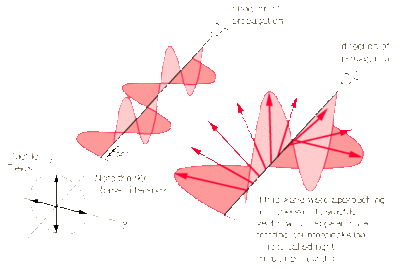
Elliptical Polarization
Elliptical polarization is very similar to circular polarization. In this case, shown to the right, the electric fields are still perpendicular and of the same amplitude. The difference is that the electric fields do not have equal amplitudes. Therefore the electric field vector creates an elliptical shape as the wave progresses - due to the changing magnitude and direction.
Mathematical Models
Linear Model
The linear model only consists of a single electric field wave.
Circular Model
The circular model consists of two components that are perpendicular, 90 degrees out of phase, and equal amplitude.
Elliptical Model
The elliptical model consists of two components that are perpendicular, 90 degrees out of phase, with different amplitude.
Examples
Determining Polarization
Below are the equations for calculating the major and minor axes of the ellipse, a and b, respectively. (Note that Beta is the phase shift between wave components.)
A) What shape does the electric field vector form when Beta = 0?
- When Beta = 0 there exists no phase shift between waves. Therefore the wave is linearly polarized.
B) What shape does the electric field vector form when a = b = E*root(2)?
- When a is equal to b, the major and minor axes of the ellipse are equal. As a and b approach equality, the ellipse becomes a circle. Therefore the wave is circularly polarized.
C) A wave consists of two components. Both are described by cosine functions with equal coefficients. The argument of the first cosine function is (wt-kz)
- and the second is (wt-kz+pi/2). What shape does the electric field vector form?
- If the cosine functions had the same argument then the shape would be linear (diagonal). In this case the second cosine function is shifted by pi/2 or 180 degrees.
- As a result the two waves are shifted and have equal amplitude. Therefore the wave is circularly polarized.
Application
Electromagnetic polarization is a fundamental concept of light. Anything we see with our eyes is affected by the polarization of light. Most people are familiar with polarized sunglasses which reduce glare from reflected light, but there are many other applications. Three dimensional movie projections use polarized filters on two projectors and polarized glasses to show a single perspective to each eye. Polarized filters are also used to analyse stress in plastics. Shining light through filters and the plastic displays color bands describing the plastic's structure. The technology is also used in geology. Geologists use microscopes with polarized lenses which allow them to identify different types of materials. Polarization is used in analyzing cosmic radiation as well. Scientists use this information to study the early universe.
History
The theory of electromagnetic waves was created in the 19th century as a result of knowledge of Electric and Magnetic fields. Scientists such as Faraday knew that magnetic fields created electric current and that electric currents produced magnetic fields. The idea behind EM waves was that electric fields and magnetic fields could alternate and propagate through space. The problem was that space had no medium for the wave to travel through. This problem was solved by James Clarke Maxwell when he proposed that electric current could travel through space if it did so at high speed. At this point Maxwell realized that this wave was light. Later, Heinrich Hertz learned that electric current in a wire could produce these EM waves. Since then, scientists have developed ways to produce and receive EM waves. This unlocked our understanding of the electromagnetic spectrum.
See also
Further reading
Transverse and Longitudinal Waves
External links
References
http://www.slideshare.net/pabitadhungel321/polarization-and-its-application
https://en.wikipedia.org/wiki/Linear_polarization
http://farside.ph.utexas.edu/teaching/315/Waves/node50.html
http://hyperphysics.phy-astr.gsu.edu/hbase/phyopt/polclas.html