Resistors and Conductivity: Difference between revisions

Latest revision as of 19:02, 30 November 2015

A resistor is a component of a circuit that acts to reduce both the flow of current and the voltage levels within the circuit. When current runs through a resistor, the energy stored within particles is converted to another form of energy, typically indicated by the emission of light or heat. Conductivity is a property of a given material that refers to the material's ability to transmit electricity. Conductivity and resistivity are opposites; that is, the higher the conductivity of a material, the less resistance it offers to the flow of current.

Relevant Equations

The resistance of a material can be calculated in several ways. The most common method relates resistance to the potential difference and the conventional current of the circuit, using the equation

[math]\displaystyle{ R = {\frac{ΔV}{I}} }[/math]

where ΔV is the potential difference across the resistor and I is the conventional current running through the circuit.

The conductivity of a material can be found using the equation

[math]\displaystyle{ σ = |q|nu = {\frac{\vec{J}}{\vec{E}}} }[/math]

where |q| is the absolute value of the charge on each carrier, n is the number of charge carriers per m³, and u is the mobility of the charge carriers, J is the current density (I/A) in A/m², and E is the electric field due to charges outside the material.

Another equation used to quantify resistance relates it to certain properties of the material and geometric properties of the resistor itself:

[math]\displaystyle{ R = {\frac{L}{σA}} }[/math]

where L is the length of the resistor, σ is the conductivity of the material, and A is the cross-sectional area of the resistor. This equation clearly demonstrates that resistivity and conductivity are inverses, as the conductivity constant can be found in the denominator.

Ohmic vs. Non-Ohmic Resistors

Based on the equations above, it is clear that both conductivity and resistance are dependent on the mobility of the charge carriers, and so these values may vary as the current through an object changes. When the conductivity of a material is nearly constant, independent of the amount of current flowing through the resistor, we consider the material and resistor "ohmic." No matter is truly ohmic, as conductivity depends to some extent on temperature, and higher currents often lead to higher temperatures. Materials are generally considered ohmic, however, if the temperature change is minimal.

Symbol and Units

The conventional symbol for a resistor used in electrical circuit diagrams is shown below.

The unit of resistance is the ohm (Ω), and the unit for conductivity is the Siemen per meter (S/m).

Resistors in Series

When ohmic resistors are connected along a single path with no branches, as in the figure below, they are said to be in series.

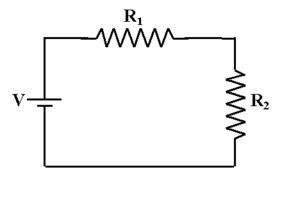
Resistors in series are, in practice, equivalent to a single resistor with the combined resistance of its constituent resistors. In other words,

[math]\displaystyle{ R_{equivalent} = R_1 + R_2 + R_3 + ... + R_n }[/math]

for n resistors in series.

Because R = L/(σA), if every resistor is composed of the same material and has the same cross-sectional area,

[math]\displaystyle{ L_{equivalent} = L_1 + L_2 + L_3 + ... + L_n }[/math]

for n resistors in series.

Resistors in Parallel

When ohmic resistors are not connected in series, they can be connected in parallel (as in the figure below), creating several branches within a circuit.

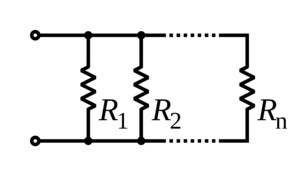
Several resistors in parallel are, in practice, equivalent to a single resistor with a resistance that is the reciprocal of the sum of reciprocals of the individual resistances. In other words,

[math]\displaystyle{ {\frac{1}{R_{equivalent}}} = {\frac{1}{R_1}} + {\frac{1}{R_2}} + {\frac{1}{R_3}} + ... + {\frac{1}{R_n}} }[/math]

for n resistors in parallel.

Because 1/R = (σA)/L, if every resistor is composed of the same material and has the same length,

[math]\displaystyle{ A_{equivalent} = A_1 + A_2 + A_3 + ... + A_n }[/math]

for n resistors in parallel.

Examples

In Series

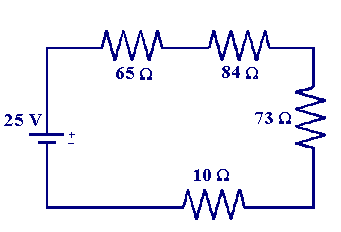
Because the circuit at left has no branches, the resistors can be considered in series. As such, the values of the resistance of the individual resistors can be summed to find the equivalent resistance. Thus,

[math]\displaystyle{ R_{equivalent} = R_1 + R_2 + R_3 + R_4 }[/math]

[math]\displaystyle{ R_{equivalent} = 65 \ Ω + 84 \ Ω + 73 \ Ω + 10 \ Ω }[/math]

[math]\displaystyle{ R_{equivalent} = 232 \ Ω }[/math]

Using this equivalent resistance and the given voltage (25 V), it is possible to find the value of the current running through the circuit after passing through the resistors.

[math]\displaystyle{ I = {\frac{ΔV}{R_{equivalent}}} = {\frac{25 \ V}{232 \ Ω}} \approx 0.108 \ A }[/math]

In Parallel

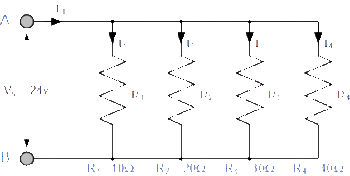
Because the circuit at right has several possible paths of current, the resistors can be considered in parallel.

As a result,

[math]\displaystyle{ {\frac{1}{R_{equivalent}}} = {\frac{1}{R_1}} + {\frac{1}{R_2}} + {\frac{1}{R_3}} + {\frac{1}{R_4}} }[/math]

[math]\displaystyle{ {\frac{1}{R_{equivalent}}} = {\frac{1}{10 \ Ω}} + {\frac{1}{20 \ Ω}} + {\frac{1}{30 \ Ω}} + {\frac{1}{40 \ Ω}} }[/math]

[math]\displaystyle{ {\frac{1}{R_{equivalent}}} = {\frac{25}{120}} \ Ω }[/math]

[math]\displaystyle{ R_{equivalent} = 4.8 \ Ω }[/math]

The voltage is again provided, and so it is possible to determine the total current I_T using ΔV and R_equivalent:

[math]\displaystyle{ I_T = {\frac{ΔV}{R_{equivalent}}} = {\frac{24 \ V}{4.8 \ Ω}} = 5 \ A }[/math]

The total current I_T can also be found by summing the currents I₁, I₂, I₃, and I₄ running through each branch. The values of these currents can be obtained using the given voltage and the individual resistances within each branch.

Applications

Light Bulbs

One of the most common applications of the concept of resistance is the incandescent light bulb. In such a light bulb, electricity is forced through a region of tungsten, which acts as a resistor. The energy in the particles is emitted as heat and light.

Heaters

Another instance of the use of resistors in real life is heating. Heat is produced by the interaction of electrons as they flow through the resistor, essentially generating heat via friction.

Other Examples

Other applications of resistance include polygraph machines, radios, televisions, circuit boards, USB drives, and toasters. Any electronic with a circuit board, such as a cell phone or laptop, most likely utilizes a resistor of some type.

References

Created by Kevin Jones, 26 November 2015

@@ Line 3: / Line 3: @@
 ==Relevant Equations==
-The resistance of a material can be calculated in several ways. The most common method relates resistance to the potential difference and the conventional current of the circuit, using the equation <math>R = {\frac{ΔV}{I}}</math> where ΔV is the potential difference across the resistor and I is the conventional current running through the circuit.
+The resistance of a material can be calculated in several ways. The most common method relates resistance to the potential difference and the conventional current of the circuit, using the equation
+<math>R = {\frac{ΔV}{I}}</math>
-The conductivity of a material can be found using the equation <math>&sigma; = |q|nu = {\frac{\vec{J}}{\vec{E}}}</math> where |''q''| is the absolute value of the charge on each carrier, ''n'' is the number of charge carriers per m<sup>3</sup>, and ''u'' is the mobility of the charge carriers, '''J''' is the current density (I/A) in A/m<sup>2</sup>, and '''E''' is the electric field due to charges outside the material.
+where ΔV is the potential difference across the resistor and I is the conventional current running through the circuit.
-Another equation used to quantify resistance relates it to certain properties of the material and geometric properties of the resistor itself: <math>R = {\frac{L}{&sigma;A}}</math> where L is the length of the resistor, &sigma; is the conductivity of the material, and A is the cross-sectional area of the resistor. This equation clearly demonstrates that resistivity and conductivity are inverses, as the conductivity constant can be found in the denominator.
+The conductivity of a material can be found using the equation
-===A Computational Model===
+<math>&sigma; = |q|nu = {\frac{\vec{J}}{\vec{E}}}</math>
-How do we visualize or predict using this topic. Consider embedding some vpython code here [https://trinket.io/glowscript/31d0f9ad9e Teach hands-on with GlowScript]
+where |''q''| is the absolute value of the charge on each carrier, ''n'' is the number of charge carriers per m<sup>3</sup>, and ''u'' is the mobility of the charge carriers, '''J''' is the current density (I/A) in A/m<sup>2</sup>, and '''E''' is the electric field due to charges outside the material.
+Another equation used to quantify resistance relates it to certain properties of the material and geometric properties of the resistor itself:
+<math>R = {\frac{L}{&sigma;A}}</math>
+where L is the length of the resistor, &sigma; is the conductivity of the material, and A is the cross-sectional area of the resistor. This equation clearly demonstrates that resistivity and conductivity are inverses, as the conductivity constant can be found in the denominator.
 ==Ohmic vs. Non-Ohmic Resistors==
@@ Line 33: / Line 41: @@
 [[File:Resistors_in_Series.png|300px|center]]
-Resistors in series are, in practice, equivalent to a single resistor with the combined resistance of its constituent resistors. In other words, <math>R_{equivalent} = R_1 + R_2 + R_3 + ... + R_n</math> for ''n'' resistors in series.
+Resistors in series are, in practice, equivalent to a single resistor with the combined resistance of its constituent resistors. In other words,
+<math>R_{equivalent} = R_1 + R_2 + R_3 + ... + R_n</math>
+for ''n'' resistors in series.
-Because R = L/(&sigma;A), if every resistor is composed of the same material and has the same cross-sectional area, <math>L_{equivalent} = L_1 + L_2 + L_3 + ... + L_n</math> for ''n'' resistors in series.
+Because R = L/(&sigma;A), if every resistor is composed of the same material and has the same cross-sectional area,
+<math>L_{equivalent} = L_1 + L_2 + L_3 + ... + L_n</math>
+for ''n'' resistors in series.
 ==Resistors in Parallel==
@@ Line 43: / Line 60: @@
 [[File:Resistors_in_Parallel.png|300px|center]]
-Several resistors in parallel are, in practice, equivalent to a single resistor with a resistance that is the reciprocal of the sum of reciprocals of the individual resistances. In other words, <math>{\frac{1}{R_{equivalent}}} = {\frac{1}{R_1}} + {\frac{1}{R_2}} + {\frac{1}{R_3}} + ... + {\frac{1}{R_n}}</math> for ''n'' resistors in parallel.
+Several resistors in parallel are, in practice, equivalent to a single resistor with a resistance that is the reciprocal of the sum of reciprocals of the individual resistances. In other words,
-Because 1/R = (&sigma;A)/L, if every resistor is composed of the same material and has the same length, <math>A_{equivalent} = A_1 + A_2 + A_3 + ... + A_n</math> for ''n'' resistors in parallel.
+<math>{\frac{1}{R_{equivalent}}} = {\frac{1}{R_1}} + {\frac{1}{R_2}} + {\frac{1}{R_3}} + ... + {\frac{1}{R_n}}</math>
+for ''n'' resistors in parallel.
+Because 1/R = (&sigma;A)/L, if every resistor is composed of the same material and has the same length,
+<math>A_{equivalent} = A_1 + A_2 + A_3 + ... + A_n</math>
+for ''n'' resistors in parallel.
 ==Examples==
-Be sure to show all steps in your solution and include diagrams whenever possible
+===In Series===
-===In Series===
+[[File:Resistors_in_Series_Example.gif|350px|left]] Because the circuit at left has no branches, the resistors can be considered in series. As such, the values of the resistance of the individual resistors can be summed to find the equivalent resistance. Thus,
-[[File:Resistors_in_Series_Example.gif|350px|left]] Because the circuit at left has no branches, the resistors can be considered in series. As such, in order to find the equivalent resistance, the values of the resistance of the individual resistors can be summed. Thus,
 <math>R_{equivalent} = R_1 + R_2 + R_3 + R_4</math>
-<math>R_{equivalent} = 65  &Omega; + 84  &Omega; + 73  &Omega; + 10  &Omega;</math>
+<math>R_{equivalent} = 65 \ &Omega; + 84 \ &Omega; + 73 \ &Omega; + 10 \ &Omega;</math>
+<math>R_{equivalent} = 232 \ &Omega;</math>
+Using this equivalent resistance and the given voltage (25 V), it is possible to find the value of the current running through the circuit after passing through the resistors.
+<math>I = {\frac{&Delta;V}{R_{equivalent}}} = {\frac{25 \ V}{232 \ &Omega;}} \approx 0.108 \ A</math>
 ===In Parallel===
-==Connectedness==
+[[File:Resistors_in_Parallel_Example.gif|350 px|right]] Because the circuit at right has several possible paths of current, the resistors can be considered in parallel.
-#How is this topic connected to something that you are interested in?
+As a result,
-#How is it connected to your major?
-#Is there an interesting industrial application?
+<math>{\frac{1}{R_{equivalent}}} = {\frac{1}{R_1}} + {\frac{1}{R_2}} + {\frac{1}{R_3}} + {\frac{1}{R_4}}</math>
+<math>{\frac{1}{R_{equivalent}}} = {\frac{1}{10 \ &Omega;}} + {\frac{1}{20 \ &Omega;}} + {\frac{1}{30 \ &Omega;}} + {\frac{1}{40 \ &Omega;}}</math>
+<math>{\frac{1}{R_{equivalent}}} = {\frac{25}{120}} \ &Omega;</math>
+<math>R_{equivalent} = 4.8 \ &Omega;</math>
+The voltage is again provided, and so it is possible to determine the total current I<sub>T</sub> using &Delta;V and R<sub>equivalent</sub>:
+<math>I_T = {\frac{&Delta;V}{R_{equivalent}}} = {\frac{24 \ V}{4.8 \ &Omega;}} = 5 \ A</math>
+The total current I<sub>T</sub> can also be found by summing the currents I<sub>1</sub>, I<sub>2</sub>, I<sub>3</sub>, and I<sub>4</sub> running through each branch. The values of these currents can be obtained using the given voltage and the individual resistances within each branch.
-==History==
+==Applications==
-Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.
+===Light Bulbs===
+One of the most common applications of the concept of resistance is the incandescent light bulb. In such a light bulb, electricity is forced through a region of tungsten, which acts as a resistor. The energy in the particles is emitted as heat and light.
+===Heaters===
+Another instance of the use of resistors in real life is heating. Heat is produced by the interaction of electrons as they flow through the resistor, essentially generating heat via friction.
+===Other Examples===
+Other applications of resistance include polygraph machines, radios, televisions, circuit boards, USB drives, and toasters. Any electronic with a circuit board, such as a cell phone or laptop, most likely utilizes a resistor of some type.
 == See also ==
-Are there related topics or categories in this wiki resource for the curious reader to explore?  How does this topic fit into that context?
+*[[Components]]
+*[[Steady State]]
+*[[Non Steady State]]
+*[[Node Rule]]
+*[[Loop Rule]]
+*[[Power in a circuit]]
+*[[Current]]
+*[[Georg Ohm]]
+==Further Reading==
-===Further reading===
+*[http://www.resistorguide.com/e-book/ The Resistor Guide E-book]
+*[http://www.barnesandnoble.com/w/resistor-theory-and-technology-felix-zandman/1101658170?ean=9781891121128 Resistor Theory and Technology, Ed. 1]
+*[http://www.amazon.com/The-Resistor-Handbook-Cletus-Kaiser/dp/0962852554 The Resistor Handbook]
-Books, Articles or other print media on this topic
+==References==
-===External links===
+#http://components.about.com/od/Components/a/Resistor-Applications.htm
+#http://www.qrg.northwestern.edu/projects/vss/docs/thermal/3-whats-a-resistor.html
+#http://www.resistorguide.com/books/
+#http://www.electronics-tutorials.ws/resistor/res50.gif?81223b
+#http://www.ceb.cam.ac.uk/data/images/groups/CREST/Teaching/impedence/series2.gif
+#https://upload.wikimedia.org/wikipedia/commons/thumb/e/ee/Resistor_symbol_America.svg/2000px-Resistor_symbol_America.svg.png
-Internet resources on this topic
-==References==
+Created by Kevin Jones, 26 November 2015
-This section contains the the references you used while writing this page
-[[Category:Which Category did you place this in?]]
+[[Category:Simple Circuits]]