Proof of Gauss's Law: Difference between revisions
Dboyadjiev3 (talk | contribs) |
|||
| (71 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
Claimed by Dea Boyadjiev (Fall 2016) | |||
In physics, Gauss's Law is one of Maxwell's four equations which describes how the electric field behaves around electric charges. Gauss's law can be derived from Coulomb's law, and vice versa. | |||
== Main Idea == | |||
Gauss's Law is defined as:<br> | |||
[[File:Gauss.png]] | |||
where <math>\phi_\text{el}</math> is electric flux, ''E'' is electric field, ''A'' is the surface area projected in the plane that's perpendicular to the field, ''Q'' is charge enclosed, and <math>\epsilon</math> is permittivity. | |||
The integral form of Gauss's Law is defined as:<br> | |||
[[File:Gaussint.png]]<br> | |||
where the area integral of the electric field vector ''E'' over any closed surface equals ''Q'', net charge enclosed in the surface, divided by <math>\epsilon</math>, permittivity of space. | |||
Gauss's | In order to provide a formal proof of the correctness of Gauss's Law, we must address the following issues:<br> | ||
1) The electric field is proportional with the inside charge by a constant of <math>\epsilon ^{-1}</math>.<br> | |||
2) The size and the shape of the surface that you choose to enclose the charge do not affect Gauss's Law.<br> | |||
3) Gauss's law works for any number of point charges within the closed surface.<br> | |||
4) Any charges that are found outside of the closed surface do not contribute to the net flux.<br> | |||
== Proof of Gauss's Law == | |||
Gauss's law works backwards into finding out what charge is present inside a 3D surface, by looking at the pattern of the electric field. The properties of Gauss's law can be confirmed through the following proofs and examples. | |||
===Determining the Proportionality Constant=== | |||
We know that the formula for Gauss's law is the sum of the Electric field (perpendicular to the surface) multiplied by the area of the surface is equal to the total inside charge times <math>\epsilon ^{-1}</math>. | |||
[https://www.google.com/url?sa=i&rct=j&q=&esrc=s&source=images&cd=&cad=rja&uact=8&ved=0ahUKEwiHkcivocbJAhVG7SYKHatuDWgQjRwIBw&url=http%3A%2F%2Fhyperphysics.phy-astr.gsu.edu%2Fhbase%2Felectric%2Fgaulaw.html&psig=AFQjCNGJcR08yEzIuQf63vfY94kAkqYJmw&ust=1449457834722579] | [https://www.google.com/url?sa=i&rct=j&q=&esrc=s&source=images&cd=&cad=rja&uact=8&ved=0ahUKEwiHkcivocbJAhVG7SYKHatuDWgQjRwIBw&url=http%3A%2F%2Fhyperphysics.phy-astr.gsu.edu%2Fhbase%2Felectric%2Fgaulaw.html&psig=AFQjCNGJcR08yEzIuQf63vfY94kAkqYJmw&ust=1449457834722579] | ||
The constant | The constant <math>\epsilon</math> can be confirmed by an experiment. When you choose to enclose a point charge by a sphere, the electric field is uniform around the entire surface of the sphere (assuming the point charge is in the center of the sphere). The electric field is also perpendicular at every point of the sphere because a point charge has an electric field pointing away from the charge in every direction (if it is positive). So the total electric flux is equal to <math>\frac{1}{4\pi \epsilon}\frac{q}{r^2}(4\pi r^2)</math>. When we set that equal to the inside charge times <math>k</math> (a constant) - we find that the constant must be <math>\epsilon ^{-1}</math>. | ||
The size of the surface doesn't matter, because the | ===The Size of the Surface Doesn't Matter=== | ||
The size of the surface doesn't matter, because the radius of both the surface as well as the radius of the electric field equation change simultaneously. They cancel each other out and the radius doesn't appear in the Gauss's law equation. | |||
===The Shape of the Surface Doesn't Matter=== | |||
The shape of the surface doesn't matter either. The electric flux is the sum of all the electric perpendicular fields at a small area on the surface. The shape will not affect the results. | The shape of the surface doesn't matter either. The electric flux is the sum of all the electric perpendicular fields at a small area on the surface. The shape will not affect the results. | ||
Any charges outside of the enclosed surface doesn't affect the result. It produces negative flux on the side of the surface that it is closest too, but it produces positive flux a the opposite side, so in the end it ends up cancelling each other out. | ===Charges Outside the Surface Contribute Zero Net Flux=== | ||
Any charges outside of the enclosed surface doesn't affect the result. It produces negative flux on the side of the surface that it is closest too, but it produces positive flux a the opposite side, so in the end it ends up cancelling each other out. | |||
===Proof of Gaussian Theorem=== | |||
Let's assume as a first principle '''Coulomb's Law''' is<br> | |||
[[File: Coulomb.png]]<br> | |||
for some point charge ''q'' where ''r''-hat is the direction of ''r'' in spherical coordinates.<br> | |||
Let's assume as a second principle '''Gauss's Law''' is<br> | |||
[[File: Gauss2.png]]<br> | |||
where the surface integral of electrostatic field over a closed surface is equal to total charge ''Q'' contained in the surface divided by <math>\epsilon</math> which is equal to total electric flux over the closed surface ''A'' in vacuum.<br> | |||
The '''Gaussian surface''' is the surface chosen to calculate the surface integral.<br> | |||
The flux is<br> | |||
[[File: Gauss3.png]]<br> | |||
where delta ''A'' is area element, ''r''-hat is in the direction along the radius vector from the center to the area element.<br> | |||
The area element and ''r''-hat have the same direction because the normal to a sphere at every point is along the radius vector at that same point. Thus,<br> | |||
[[File: Gauss4.png]]<br> | |||
The magnitude of the ''r''-hat is 1. The total flux through the sphere is calculated by summing up the flux through all various area elements. Each area element of the sphere is the same distance from the charge. <br> | |||
[[File: Gauss5.png]]<br> | |||
The total surface area of a sphere is <math>4\pi r^2</math>. Thus,<br> | |||
[[File: Gauss6.png]] | |||
== Connectedness == | |||
This topic is connected to something I am interested in as I like that we can work backwards into finding the source of the electric field that is present. It is not directly connected to my major of Nuclear and Radiological Engineering as quantum physics tends to play more of a role than electricity and magnetism. The problem solving side of proving Gauss's law can be connected to any type of engineering. | |||
Gauss's Law is helpful in finding the electric field only when the charge is distributed symmetrically. Coulomb's Law is fundamental, but Gauss's Law is theoretically not needed. There is no application of Gauss's Law per se, but it is a powerful tool in terms of simplifying calculations and difficult situations. | |||
== History == | |||
The theorem was first discovered by Lagrange in 1773, followed by Gauss in 1813. | |||
== See Also == | |||
=== Further reading === | |||
[[Gauss's Law]]<br> | |||
[[Coulomb's law]] | |||
===External links=== | |||
Gauss's law[https://en.wikipedia.org/wiki/Gauss's_law] | |||
== References == | |||
Gauss's Law[http://hyperphysics.phy-astr.gsu.edu/hbase/electric/gaulaw.html]<br> | |||
Gauss's law[https://en.wikipedia.org/wiki/Gauss's_law]<br> | |||
What is the proof for Gauss's law for electricity for general closed surfaces?[https://www.quora.com/What-is-the-proof-for-Gausss-law-for-electricity-for-general-closed-surfaces]<br> | |||
Gauss's Theorem and its Proof[http://dmr-physicsnotes.blogspot.com/2012/12/gausss-theorem-and-its-proof.html]<br> | |||
[[Category:Gauss's Law]] | |||
Latest revision as of 01:05, 27 November 2016
Claimed by Dea Boyadjiev (Fall 2016)
In physics, Gauss's Law is one of Maxwell's four equations which describes how the electric field behaves around electric charges. Gauss's law can be derived from Coulomb's law, and vice versa.
Main Idea
Gauss's Law is defined as:
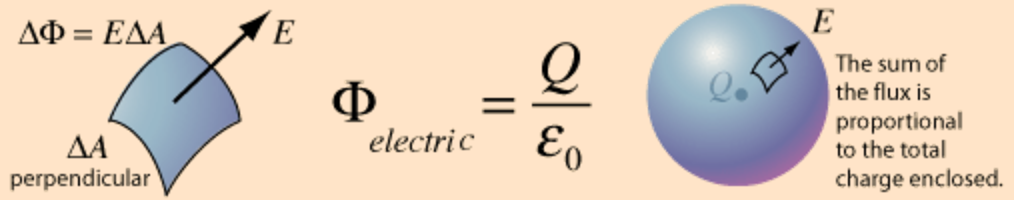 where [math]\displaystyle{ \phi_\text{el} }[/math] is electric flux, E is electric field, A is the surface area projected in the plane that's perpendicular to the field, Q is charge enclosed, and [math]\displaystyle{ \epsilon }[/math] is permittivity.
where [math]\displaystyle{ \phi_\text{el} }[/math] is electric flux, E is electric field, A is the surface area projected in the plane that's perpendicular to the field, Q is charge enclosed, and [math]\displaystyle{ \epsilon }[/math] is permittivity.
The integral form of Gauss's Law is defined as:
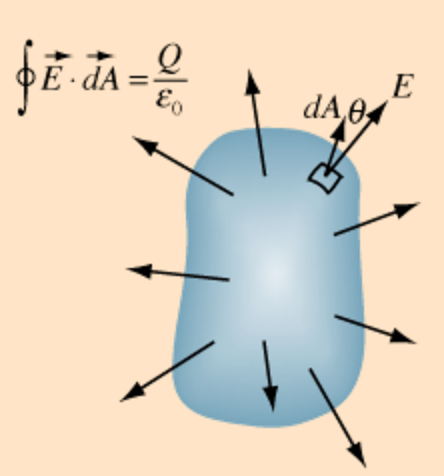
where the area integral of the electric field vector E over any closed surface equals Q, net charge enclosed in the surface, divided by [math]\displaystyle{ \epsilon }[/math], permittivity of space.
In order to provide a formal proof of the correctness of Gauss's Law, we must address the following issues:
1) The electric field is proportional with the inside charge by a constant of [math]\displaystyle{ \epsilon ^{-1} }[/math].
2) The size and the shape of the surface that you choose to enclose the charge do not affect Gauss's Law.
3) Gauss's law works for any number of point charges within the closed surface.
4) Any charges that are found outside of the closed surface do not contribute to the net flux.
Proof of Gauss's Law
Gauss's law works backwards into finding out what charge is present inside a 3D surface, by looking at the pattern of the electric field. The properties of Gauss's law can be confirmed through the following proofs and examples.
Determining the Proportionality Constant
We know that the formula for Gauss's law is the sum of the Electric field (perpendicular to the surface) multiplied by the area of the surface is equal to the total inside charge times [math]\displaystyle{ \epsilon ^{-1} }[/math].
The constant [math]\displaystyle{ \epsilon }[/math] can be confirmed by an experiment. When you choose to enclose a point charge by a sphere, the electric field is uniform around the entire surface of the sphere (assuming the point charge is in the center of the sphere). The electric field is also perpendicular at every point of the sphere because a point charge has an electric field pointing away from the charge in every direction (if it is positive). So the total electric flux is equal to [math]\displaystyle{ \frac{1}{4\pi \epsilon}\frac{q}{r^2}(4\pi r^2) }[/math]. When we set that equal to the inside charge times [math]\displaystyle{ k }[/math] (a constant) - we find that the constant must be [math]\displaystyle{ \epsilon ^{-1} }[/math].
The Size of the Surface Doesn't Matter
The size of the surface doesn't matter, because the radius of both the surface as well as the radius of the electric field equation change simultaneously. They cancel each other out and the radius doesn't appear in the Gauss's law equation.
The Shape of the Surface Doesn't Matter
The shape of the surface doesn't matter either. The electric flux is the sum of all the electric perpendicular fields at a small area on the surface. The shape will not affect the results.
Charges Outside the Surface Contribute Zero Net Flux
Any charges outside of the enclosed surface doesn't affect the result. It produces negative flux on the side of the surface that it is closest too, but it produces positive flux a the opposite side, so in the end it ends up cancelling each other out.
Proof of Gaussian Theorem
Let's assume as a first principle Coulomb's Law is
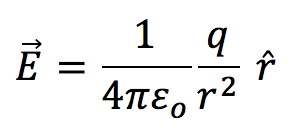
for some point charge q where r-hat is the direction of r in spherical coordinates.
Let's assume as a second principle Gauss's Law is
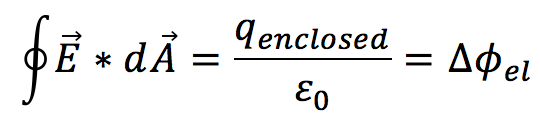
where the surface integral of electrostatic field over a closed surface is equal to total charge Q contained in the surface divided by [math]\displaystyle{ \epsilon }[/math] which is equal to total electric flux over the closed surface A in vacuum.
The Gaussian surface is the surface chosen to calculate the surface integral.
The flux is
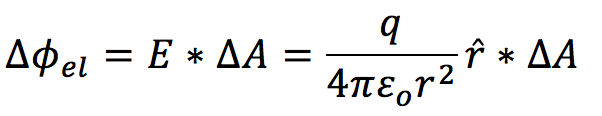
where delta A is area element, r-hat is in the direction along the radius vector from the center to the area element.
The area element and r-hat have the same direction because the normal to a sphere at every point is along the radius vector at that same point. Thus,
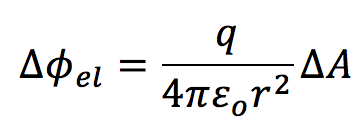
The magnitude of the r-hat is 1. The total flux through the sphere is calculated by summing up the flux through all various area elements. Each area element of the sphere is the same distance from the charge.
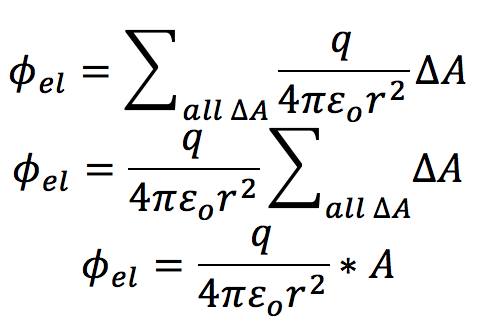
The total surface area of a sphere is [math]\displaystyle{ 4\pi r^2 }[/math]. Thus,
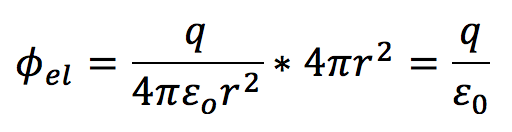
Connectedness
This topic is connected to something I am interested in as I like that we can work backwards into finding the source of the electric field that is present. It is not directly connected to my major of Nuclear and Radiological Engineering as quantum physics tends to play more of a role than electricity and magnetism. The problem solving side of proving Gauss's law can be connected to any type of engineering. Gauss's Law is helpful in finding the electric field only when the charge is distributed symmetrically. Coulomb's Law is fundamental, but Gauss's Law is theoretically not needed. There is no application of Gauss's Law per se, but it is a powerful tool in terms of simplifying calculations and difficult situations.
History
The theorem was first discovered by Lagrange in 1773, followed by Gauss in 1813.
See Also
Further reading
External links
Gauss's law[2]
References
Gauss's Law[3]
Gauss's law[4]
What is the proof for Gauss's law for electricity for general closed surfaces?[5]
Gauss's Theorem and its Proof[6]