Current in an LC Circuit: Difference between revisions

Latest revision as of 23:57, 13 April 2025

CLAIMED BY: Rafay Hadi (Spring 2025)

An LC circuit is a simple but powerful electrical system composed of an inductor (L) and a capacitor (C) connected together in a closed loop. Despite its simplicity, the LC circuit exhibits rich dynamic behavior due to the interplay between the electric and magnetic fields stored in the capacitor and inductor, respectively. The capacitor stores energy in the form of an electric field between its plates, while the inductor stores energy in the magnetic field generated by the current flowing through it.

When the switch in an LC circuit is closed and the capacitor is initially charged, the voltage across the capacitor drives a current through the inductor. However, the inductor resists sudden changes in current—this property, known as inductive inertia, causes the current to build up gradually. At the same time, the capacitor's voltage begins to decrease as it discharges, but it too cannot change instantaneously. This mutual resistance to change results in a smooth, continuous transfer of energy: the capacitor's electric field gradually gives way to a growing magnetic field in the inductor.

Because the circuit contains no resistive elements, there is no energy loss to heat. Instead, the energy oscillates back and forth between the capacitor and the inductor indefinitely. This results in an ongoing current oscillation, much like a frictionless mass-spring system in mechanics. The frequency of this oscillation depends only on the values of the inductance L and capacitance C, and is given by:

[math]\displaystyle{ \omega = \frac{1}{\sqrt{LC}} }[/math]

This natural frequency of oscillation is the hallmark of resonance in LC circuits and forms the basis for applications in signal processing, radio communications, and filtering systems.

The Main Idea

An LC circuit is a fundamental building block in electronics, consisting of just two components: an inductor (L) and a capacitor (C), connected in a closed loop. These components store energy in different ways—capacitors store energy in electric fields, while inductors store energy in magnetic fields. When connected together, they create an oscillating system where energy shifts back and forth between these two forms.

How It Works

Initially, the capacitor is fully charged. When a switch closes, it begins to discharge, releasing energy into the circuit. However, the inductor resists sudden changes in current (a property known as inductance), so the current doesn't jump instantly to a high value—it increases gradually. As the capacitor discharges, the energy it stored is transferred into the magnetic field of the inductor.

Once the capacitor is fully discharged, the current is at its maximum. But the inductor doesn’t allow the current to stop abruptly, so it keeps pushing current through the circuit—recharging the capacitor with opposite polarity. This starts the cycle in reverse.

This back-and-forth exchange of energy continues in a sinusoidal oscillation pattern. In an ideal LC circuit with no resistance, this oscillation would continue forever.

At the moment the capacitor runs out of charge, there is a current in the inductor, and because inductors are sluggish by nature, the current can't immediately change to zero. Therefore, the system does not come to equilibrium and instead increases the charge in the capacitor. When the capacitor is fully charged, it starts to discharge back through the inductor, and the process repeats. Since the circuit will never reach equilibrium and current never reaches zero, this oscillating process repeats forever. Oscillations could reach a stopping point if there is some resistance, but it may still go through multiple cycles before equilibrium is reached.

Why this is special

A series LC circuit—where the inductor and capacitor are connected end-to-end—exhibits behaviors that differ from non-oscillating circuits. For example:

In RC circuits, voltage or charge decays exponentially toward equilibrium.

In LC circuits, charge and current vary periodically, resembling sine or cosine functions.

Because energy is conserved and exchanged smoothly between the inductor and capacitor, LC circuits can oscillate continuously if resistance is small. That’s why LC circuits typically use low-resistance, thick copper wires to minimize energy loss.

A Mathematical Model

An LC circuit has an energy conservation rule associated with it. The energy conservation loop rule for an LC circuit is: [math]\displaystyle{ \Delta V_{capacitor} + \Delta V_{inductor} = \frac{Q}{C}-L\frac{dI}{dt} = 0 }[/math] where [math]\displaystyle{ Q }[/math] is the charge on the upper plate of the capacitor and [math]\displaystyle{ I }[/math] is the conventional current leaving the upper plate and going through the inductor.

[math]\displaystyle{ dQ/dt }[/math] is the amount of charge flowing off the capacitor every second. This is the same as the current. Because the charge is leaving the capacitor, [math]\displaystyle{ I = -\frac{dQ}{dt} }[/math].

Energy conservation can be re-written as [math]\displaystyle{ \frac{1}{C}Q+L\frac{d^{2}Q}{dt^{2}} = 0 }[/math]

In addition, by substituting Q and its second derivative into the equation, a possible solution of the rewritten energy conservation equation is [math]\displaystyle{ Q = Q_{i}cos(\frac{1}{\sqrt{LC}}t) }[/math]

Therefore, the current is given by: [math]\displaystyle{ I = -\frac{dQ}{dt} = \frac{Q_{i}}{\sqrt{LC}}sin(\frac{1}{\sqrt{LC}}t) }[/math]

A Computational Model

Click here to view a glowscript simulation of the oscillation of an LC Circuit! Please scroll down to view the graphs

Summary

Some synonyms commonly used for an LC circuit include tank circuit, tuned circuit, and resonant circuit—all highlighting its key role in frequency selection and oscillation.

An LC circuit is a fundamental electrical system composed of an inductor (L) and a capacitor (C) connected in a closed loop. Unlike RC or RL circuits, which gradually approach equilibrium or steady-state current, an LC circuit exhibits continuous, undamped oscillations of charge and current due to the exchange of energy between the electric field in the capacitor and the magnetic field in the inductor.

These oscillations occur at a natural angular frequency given by:

[math]\displaystyle{ \omega = \frac{1}{\sqrt{LC}} }[/math]

where [math]\displaystyle{ L }[/math] is the inductance and [math]\displaystyle{ C }[/math] is the capacitance. The behavior of the circuit is analogous to that of a mass-spring system in mechanics, with energy continuously shifting between kinetic and potential forms.

LC circuits demonstrate several important concepts in electromagnetism, including energy conservation, resonance, and the interplay between electric and magnetic fields. Because the circuit is idealized to have no resistance, the oscillations theoretically persist forever.

In practical terms, LC circuits are essential in a wide variety of applications including signal filtering, radio tuning, voltage and current magnification, oscillators, and resonant power systems. Their frequency-selective properties make them vital building blocks in analog electronics, RF systems, and power electronics.

Comparison to a Spring

As stated above, An LC circuit is a closed electrical loop made up of just two components: a capacitor (C) and an inductor (L). Like a mass on a spring, this system exhibits resonance—there’s a natural frequency at which it prefers to oscillate, and when driven at that frequency, it responds with large amplitude oscillations.

In this circuit, electric charge oscillates back and forth, much like how a mass oscillates around an equilibrium position on a spring. The analogy extends to the key parameters that define each system:

Mass m is analogous to inductance L

Spring displacement x is analogous to charge Q

Velocity v=dx/dt corresponds to current I=dQ/dt

Spring stiffness k relates to the inverse of capacitance 1/C

Just as a spring-mass system has a natural frequency [math]\displaystyle{ \omega = \sqrt{\frac{k}{m}} }[/math], an LC circuit resonates at a characteristic angular frequency

[math]\displaystyle{ \omega = \frac{1}{\sqrt{LC}} }[/math]

This is the frequency at which the circuit most efficiently exchanges energy between the electric field in the capacitor and the magnetic field in the inductor.

Examples

Use the given circuit and information to solve for the following quantities:

L = 4.0 mH

C = 5.0 μF

Simple

Find the resonant frequency in radians per second and Hertz and the period in seconds:

Middling

Find the initial charge on the fully charged capacitor and the maximum current between oscillations:

Connectedness

This topic connects closely to RC and RL circuits, which exhibit exponential behavior as they approach equilibrium or steady-state conditions. In contrast, an LC circuit is fundamentally different—it does not settle into a final state. Instead, it oscillates indefinitely, with energy continually transferring between the capacitor’s electric field and the inductor’s magnetic field. The result is a continuous back-and-forth motion of charge and current, with no energy lost in an ideal LC system.

From an engineering standpoint, LC circuits are incredibly useful, particularly in electrical, electronics, and even mechanical domains. One of their most important applications is in resonance-based filtering and signal selection. When tuning a radio to a specific station, the LC circuit is configured to resonate at that station's carrier frequency, allowing it to pick out the desired signal while rejecting others. This principle underlies the operation of bandpass filters, oscillators, and frequency-selective amplifiers.

LC circuits also play a role in impedance matching in communication systems, where they help maximize power transfer between components. In power electronics, they are used for voltage and current magnification, especially at resonance, where voltages across individual components can greatly exceed the supply voltage. Another application is induction heating, where high-frequency LC circuits create rapidly changing magnetic fields that induce currents in nearby conductive materials, heating them without direct contact.

In addition, LC circuits form the core of tank circuits in oscillators, timing circuits, pulse shaping, and resonant converters used in switching power supplies. Their predictability, efficiency, and frequency-selective properties make them essential in the design of analog systems and RF technologies.

Parallel and Series

Series is shown below

Parallel is shown below

History

In 1826, French scientist Felix Savary was the first to discover evidence that a capacitor and an inductor could produce electrical oscillations. In his experiment, he discharged a Leyden jar through a wire wound around an iron needle. He found that sometimes the needle was left magnetized in one direction and other times it was in the opposite direction. He concluded that this was due to a damped oscillating discharge current in the wire, which reversed the magnetization of the needle back and forth until it was too small to have an effect, leaving the needle magnetized in a random direction.

Then in 1889, there was one of the first demonstrations of resonance with Lodge's "syntonic jars" experiment. In this experiment, two resonant circuits were next to each other, and each consisted of a Leyden jar connected to a one-turn coil with a spark gap. If a high voltage from the induction coil was then applied to one of the circuits, then sparks were excited in the other tuned circuit only when the circuits were adjusted to resonance.

LC circuits first practical use began around 1890 with spark-gap radio transmitters to allow the receiver and transmitter to be tuned to the same frequency. The first patent for a radio system that allowed tuning was filed by Lodge in 1897, and systems were invented in 1900 by Italian radio pioneer Guglielmo Marconi.

Applications

LC circuits have a wide range of applications across electronics, communication, and power systems due to their resonance properties and frequency-selective behavior. Some key applications include:

Signal Processing and Communication Systems:

LC circuits are essential in filtering signals, separating frequency bands, and selecting desired frequencies in RF (radio frequency) systems.

Tuning Radio Transmitters and Receivers:

By adjusting the values of the inductor and capacitor, LC circuits can be set to resonate at specific frequencies, allowing radios to isolate and process signals from individual stations.

Voltage and Current Magnification:

Series LC circuits are used for voltage magnification, where the voltage across components at resonance can be much greater than the input voltage. Parallel LC circuits offer current magnification, making them useful in applications where high circulating currents are desired.

Induction Heating:

Both series and parallel LC configurations are used to generate high-frequency alternating currents that produce rapidly changing magnetic fields, inducing eddy currents in metal objects and heating them efficiently.

Electronic Resonators:

LC circuits function as resonant elements in devices such as: Oscillators, where they help generate stable AC signals of specific frequencies Amplifiers, where they assist in frequency selection and signal shaping Frequency tuners, used in televisions, radios, and wireless systems

Their ability to resonate precisely at desired frequencies makes LC circuits indispensable in analog circuit design and high-frequency electronic applications.

References

Matter & Interactions 4th Edition: Electric and Magnetic Interactions

http://www.chegg.com/homework-help/questions-and-answers/x-i5rong-please-help-part-g-learning-goal-understand-processes-series-circuit-containing-i-q74127

https://en.wikipedia.org/wiki/LC_circuit

http://farside.ph.utexas.edu/teaching/315/Waves/node5.html

http://physics.info/circuits-rlc/

https://www.youtube.com/watch?v=v3-HwZMThzQ

https://www.youtube.com/watch?v=_8d4LQMFc1o

http://farside.ph.utexas.edu/teaching/315/Waves/node5.html

https://www.youtube.com/watch?v=v3-HwZMThzQ

http://www.animations.physics.unsw.edu.au/jw/LCresonance.html

Current in an LC Circuit: Difference between revisions

Latest revision as of 23:57, 13 April 2025

Contents

The Main Idea

A Mathematical Model

A Computational Model

Summary

Comparison to a Spring

Examples

Simple

Middling

Connectedness

Parallel and Series

History

Applications

See also

External links

References

Navigation menu

@@ Line 1: / Line 1: @@
-CLAIMED BY: Kelsey Dobson
-/5/2015
-An LC circuit contains an inductor and a capacitor, and because of the inductor's sluggishness and resistance to change the current, the charge in this circuit can oscillate back and forth forever.
+CLAIMED BY: Rafay Hadi (Spring 2025)
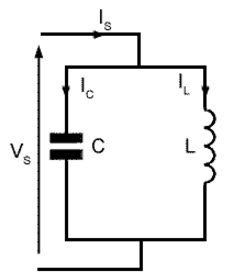
+An LC circuit is a simple but powerful electrical system composed of an inductor (L) and a capacitor (C) connected together in a closed loop. Despite its simplicity, the LC circuit exhibits rich dynamic behavior due to the interplay between the electric and magnetic fields stored in the capacitor and inductor, respectively. The capacitor stores energy in the form of an electric field between its plates, while the inductor stores energy in the magnetic field generated by the current flowing through it.
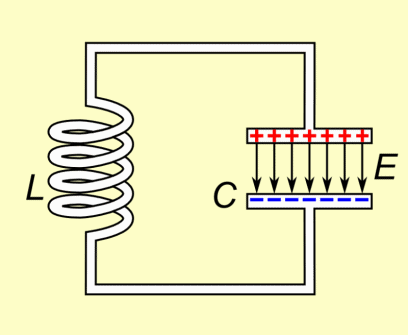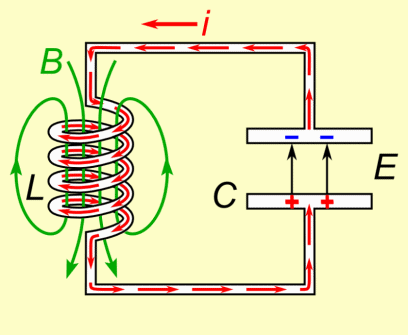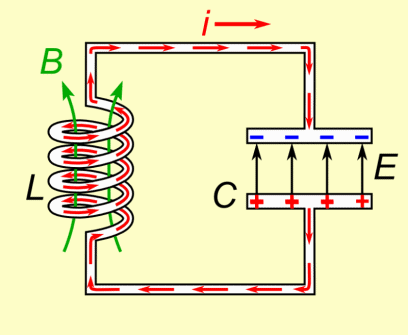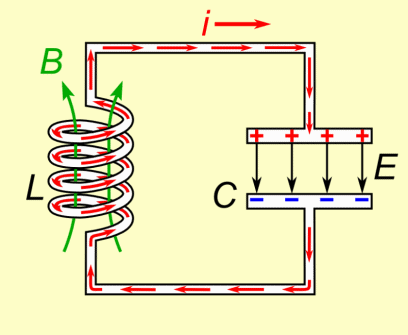
+When the switch in an LC circuit is closed and the capacitor is initially charged, the voltage across the capacitor drives a current through the inductor. However, the inductor resists sudden changes in current—this property, known as inductive inertia, causes the current to build up gradually. At the same time, the capacitor's voltage begins to decrease as it discharges, but it too cannot change instantaneously. This mutual resistance to change results in a smooth, continuous transfer of energy: the capacitor's electric field gradually gives way to a growing magnetic field in the inductor.
+Because the circuit contains no resistive elements, there is no energy loss to heat. Instead, the energy oscillates back and forth between the capacitor and the inductor indefinitely. This results in an ongoing current oscillation, much like a frictionless mass-spring system in mechanics. The frequency of this oscillation depends only on the values of the inductance L and capacitance C, and is given by:
+<math>\omega = \frac{1}{\sqrt{LC}}</math>
+This natural frequency of oscillation is the hallmark of resonance in LC circuits and forms the basis for applications in signal processing, radio communications, and filtering systems.
+[[File:220px-LC_parallel_simple.svg.png]]
 ==The Main Idea==
-A circuit containing an inductor "L" and a capacitor "C" is called an LC circuit. This circuit can oscillate continuously if the resistance is small. Accordingly, the connecting wires in an LC circuit are low-resistance thick copper wires. Here is the basic idea behind the process of an LC circuit:
+An LC circuit is a fundamental building block in electronics, consisting of just two components: an inductor (L) and a capacitor (C), connected in a closed loop. These components store energy in different ways—capacitors store energy in electric fields, while inductors store energy in magnetic fields. When connected together, they create an oscillating system where energy shifts back and forth between these two forms.
+'''How It Works'''
+Initially, the capacitor is fully charged. When a switch closes, it begins to discharge, releasing energy into the circuit. However, the inductor resists sudden changes in current (a property known as inductance), so the current doesn't jump instantly to a high value—it increases gradually. As the capacitor discharges, the energy it stored is transferred into the magnetic field of the inductor.
+Once the capacitor is fully discharged, the current is at its maximum. But the inductor doesn’t allow the current to stop abruptly, so it keeps pushing current through the circuit—recharging the capacitor with opposite polarity. This starts the cycle in reverse.
+This back-and-forth exchange of energy continues in a sinusoidal oscillation pattern. In an ideal LC circuit with no resistance, this oscillation would continue forever.
-A capacitor is charged initially, and then a switch is closed. This connects the capacitor to the inductor. At first, because of the nature of an inductor, it is difficult for charge on the capacitor to flow through the inductor. This is because the inductor opposes all attempts to change the current. However, since an inductor cannot completely prevent a current from changing, there is more current little by little. This drains the capacitor of its charge.
+At the moment the capacitor runs out of charge, there is a current in the inductor, and because inductors are sluggish by nature, the current can't immediately change to zero. Therefore, the system does not come to equilibrium and instead increases the charge in the capacitor. When the capacitor is fully charged, it starts to discharge back through the inductor, and the process repeats. Since the circuit will never reach equilibrium and current never reaches zero, this oscillating process repeats forever. Oscillations could reach a stopping point if there is some resistance, but it may still go through multiple cycles before equilibrium is reached.
-At the moment the capacitor runs out of charge, there is a current in the inductor, and because inductors are sluggish by nature, the current can't immediately change to zero. Therefore, the system does not come to equililbrium and instead increases the charge in the capacitor. When the capacitor is fully charged, it starts to discharge back through the inductor, and the process repeats. Since the circuit will never reach equilibrium and current never reaches zero, this oscillating process repeats forever. Oscillations could reach a stopping point if there is some resistance, but it may still go through multiple cycles before equilibrium is reached.
+'''Why this is special'''
+A series LC circuit—where the inductor and capacitor are connected end-to-end—exhibits behaviors that differ from non-oscillating circuits. For example:
+*In '''RC circuits''', voltage or charge decays exponentially toward equilibrium.
+*In '''LC circuits''', charge and current vary periodically, resembling sine or cosine functions.
+Because energy is conserved and exchanged smoothly between the inductor and capacitor, LC circuits can oscillate continuously if resistance is small. That’s why LC circuits typically use low-resistance, thick copper wires to minimize energy loss.
 ===A Mathematical Model===
 An LC circuit has an energy conservation rule associated with it. The energy conservation loop rule for an LC circuit is:
-<math> \delta\V_{capacitor} + \delta\V_{inductor} = \frac{1}{C}-L\frac{dI}{dt} = 0 </math>
+<math> \Delta V_{capacitor} + \Delta V_{inductor} = \frac{Q}{C}-L\frac{dI}{dt} = 0 </math> where <math>Q</math> is the charge on the upper plate of the capacitor and <math>I</math> is the conventional current leaving the upper plate and going through the inductor.
+<math>dQ/dt</math> is the amount of charge flowing off the capacitor every second. This is the same as the current. Because the charge is leaving the capacitor, <math> I = -\frac{dQ}{dt}</math>.
+Energy conservation can be re-written as <math>\frac{1}{C}Q+L\frac{d^{2}Q}{dt^{2}} = 0 </math>
+In addition, by substituting Q and its second derivative into the equation, a possible solution of the rewritten energy conservation equation is <math> Q = Q_{i}cos(\frac{1}{\sqrt{LC}}t) </math>
+Therefore, the current is given by: <math> I = -\frac{dQ}{dt} = \frac{Q_{i}}{\sqrt{LC}}sin(\frac{1}{\sqrt{LC}}t) </math>
 ===A Computational Model===
+'''[https://www.glowscript.org/#/user/rafay11hadi/folder/MyPrograms/program/LCCircuitThing Click here to view a glowscript simulation of the oscillation of an LC Circuit! Please scroll down to view the graphs]'''
+[[File:LCcircuit.jpg]]
+[[File:Tuned_circuit_animation_3_300ms.gif]]
+==Summary==
+Some synonyms commonly used for an LC circuit include tank circuit, tuned circuit, and resonant circuit—all highlighting its key role in frequency selection and oscillation.
+An '''LC circuit''' is a fundamental electrical system composed of an inductor (L) and a capacitor (C) connected in a closed loop. Unlike RC or RL circuits, which gradually approach equilibrium or steady-state current, an LC circuit exhibits continuous, undamped oscillations of charge and current due to the exchange of energy between the electric field in the capacitor and the magnetic field in the inductor.
+These oscillations occur at a natural angular frequency given by:
+<math>\omega = \frac{1}{\sqrt{LC}}</math>
+where <math>L</math> is the inductance and <math>C</math> is the capacitance. The behavior of the circuit is analogous to that of a mass-spring system in mechanics, with energy continuously shifting between kinetic and potential forms.
+LC circuits demonstrate several important concepts in electromagnetism, including energy conservation, resonance, and the interplay between electric and magnetic fields. Because the circuit is idealized to have no resistance, the oscillations theoretically persist forever.
+In practical terms, LC circuits are essential in a wide variety of applications including signal filtering, radio tuning, voltage and current magnification, oscillators, and resonant power systems. Their frequency-selective properties make them vital building blocks in analog electronics, RF systems, and power electronics.
+==Comparison to a Spring==
+As stated above, An LC circuit is a closed electrical loop made up of just two components: a capacitor (C) and an inductor (L). Like a mass on a spring, this system exhibits resonance—there’s a natural frequency at which it prefers to oscillate, and when driven at that frequency, it responds with large amplitude oscillations.
+In this circuit, electric charge oscillates back and forth, much like how a mass oscillates around an equilibrium position on a spring. The analogy extends to the key parameters that define each system:
+*Mass m is analogous to inductance L
+*Spring displacement x is analogous to charge Q
+*Velocity v=dx/dt corresponds to current I=dQ/dt
+*Spring stiffness k relates to the inverse of capacitance 1/C
+Just as a spring-mass system has a natural frequency <math>\omega = \sqrt{\frac{k}{m}}</math>, an LC circuit resonates at a characteristic angular frequency
+<math>\omega = \frac{1}{\sqrt{LC}}</math>
+This is the frequency at which the circuit most efficiently exchanges energy between the electric field in the capacitor and the magnetic field in the inductor.
 ==Examples==
+Use the given circuit and information to solve for the following quantities:
+L = 4.0 mH
+C = 5.0 μF
+[[File:WikiQ.jpg|400x400px]]
 ===Simple===
-Emf of an entire solenoid:
+Find the resonant frequency in radians per second and Hertz and the period in seconds:
-B=μ0NI/d
+[[File:WikiA1.jpg|400x400px]]
-emf = |d(mag flux)/dt| = d/dt|μ0NI/d(piR^2)| = μ0NI/d(piR^2)dI/dt
-emf = N(μ0N/d(piR^2)dI/dt)= (μ0N^2/d(piR^2)dI/dt)
 ===Middling===
-What is the self inductance of a common solenoid?
+Find the initial charge on the fully charged capacitor and the maximum current between oscillations:
+[[File:WikiA2.jpg|400x400px]]
+==Connectedness==
+This topic connects closely to RC and RL circuits, which exhibit exponential behavior as they approach equilibrium or steady-state conditions. In contrast, an LC circuit is fundamentally different—it does not settle into a final state. Instead, it oscillates indefinitely, with energy continually transferring between the capacitor’s electric field and the inductor’s magnetic field. The result is a continuous back-and-forth motion of charge and current, with no energy lost in an ideal LC system.
--The self inductance is the constant in the inductance formula solved above. This means that the self inductance constant for a solenoid is (μ0N/d(piR^2)
+From an engineering standpoint, LC circuits are incredibly useful, particularly in electrical, electronics, and even mechanical domains. One of their most important applications is in resonance-based filtering and signal selection. When tuning a radio to a specific station, the LC circuit is configured to resonate at that station's carrier frequency, allowing it to pick out the desired signal while rejecting others. This principle underlies the operation of bandpass filters, oscillators, and frequency-selective amplifiers.
-===Difficult===
+LC circuits also play a role in impedance matching in communication systems, where they help maximize power transfer between components. In power electronics, they are used for voltage and current magnification, especially at resonance, where voltages across individual components can greatly exceed the supply voltage. Another application is induction heating, where high-frequency LC circuits create rapidly changing magnetic fields that induce currents in nearby conductive materials, heating them without direct contact.
-What is the self-inductance of a solenoid that has 100 loops, a radius of 5 cm, and is 1 meter long.
+In addition, LC circuits form the core of tank circuits in oscillators, timing circuits, pulse shaping, and resonant converters used in switching power supplies. Their predictability, efficiency, and frequency-selective properties make them essential in the design of analog systems and RF technologies.
-- the self inductance would be (μ0100/1(pi.01^2)= 3.95e-8 henries
+==Parallel and Series==
-==Connectedness==
+Series is shown below
-#This topic is interesting because solenoids are a very common placed tool. It is important to know how they operate in order to use them to the best of their capabilities.
+[[File:Series-LC-Circuit-Resonance.jpg]]
-#This topic is personally connected to me because of my major. I am a mechanical engineer and am currently enrolled in ME2110, the "robot building class". In this class to assist with our designs, we often used solenoids as deployment mechanism. Being able to learn about this topic while working with the objects hands on in a non-physics environment helped me immensely in my design process and physics career.
+Parallel is shown below
+[[File:Parallel-LC-Circuit-Resonance.jpg]]
 ==History==
-The history of inductance goes back quite a long time ago and is pretty complicated. In the early 19th century there were actually two scientist discovering inductance in parallel with each other, one in America and one in England. These two scientist names are Joseph Henry and Michael Faraday. Because of this there is no one named founder of inductance, but both of them did receive credit. Inductance now finds itself as one of Faraday's Laws, giving Michael Faraday his due credit. While the units for inductance are "Henries" named after Joseph Henry.
+In 1826, French scientist Felix Savary was the first to discover evidence that a capacitor and an inductor could produce electrical oscillations. In his experiment, he discharged a Leyden jar through a wire wound around an iron needle. He found that sometimes the needle was left magnetized in one direction and other times it was in the opposite direction. He concluded that this was due to a damped oscillating discharge current in the wire, which reversed the magnetization of the needle back and forth until it was too small to have an effect, leaving the needle magnetized in a random direction.
+Then in 1889, there was one of the first demonstrations of resonance with Lodge's "syntonic jars" experiment. In this experiment, two resonant circuits were next to each other, and each consisted of a Leyden jar connected to a one-turn coil with a spark gap. If a high voltage from the induction coil was then applied to one of the circuits, then sparks were excited in the other tuned circuit only when the circuits were adjusted to resonance.
+LC circuits first practical use began around 1890 with spark-gap radio transmitters to allow the receiver and transmitter to be tuned to the same frequency. The first patent for a radio system that allowed tuning was filed by Lodge in 1897, and systems were invented in 1900 by Italian radio pioneer Guglielmo Marconi.
+==Applications==
+LC circuits have a wide range of applications across electronics, communication, and power systems due to their resonance properties and frequency-selective behavior. Some key applications include:
+*'''Signal Processing and Communication Systems''':
+LC circuits are essential in filtering signals, separating frequency bands, and selecting desired frequencies in RF (radio frequency) systems.
+*'''Tuning Radio Transmitters and Receivers''':
+By adjusting the values of the inductor and capacitor, LC circuits can be set to resonate at specific frequencies, allowing radios to isolate and process signals from individual stations.
+*'''Voltage and Current Magnification''':
+'''Series LC circuits''' are used for '''voltage magnification''', where the voltage across components at resonance can be much greater than the input voltage.
+'''Parallel LC circuits''' offer '''current magnification''', making them useful in applications where high circulating currents are desired.
+*'''Induction Heating''':
+Both series and parallel LC configurations are used to generate high-frequency alternating currents that produce rapidly changing magnetic fields, inducing eddy currents in metal objects and heating them efficiently.
+*'''Electronic Resonators''':
+LC circuits function as resonant elements in devices such as: '''Oscillators''', where they help generate stable AC signals of specific frequencies
+'''Amplifiers''', where they assist in frequency selection and signal shaping
+'''Frequency tuners''', used in televisions, radios, and wireless systems
+Their ability to resonate precisely at desired frequencies makes LC circuits indispensable in analog circuit design and high-frequency electronic applications.
 == See also ==
-Faraday's Law
-===Further reading===
+===External links===
+Helpful websites for furthering your understanding of LC circuits, including some mathematical applications:
+[http://farside.ph.utexas.edu/teaching/315/Waves/node5.html]
+[http://physics.info/circuits-rlc/]
+http://www.animations.physics.unsw.edu.au/jw/LCresonance.html
-Information for this page was found in Matter and Interactions Volume II. If you would like to know more about this topic or other topics like it, please reference this book.
+A helpful video for further information:
+[https://www.youtube.com/watch?v=v3-HwZMThzQ]
-===External links===
+https://www.youtube.com/watch?v=TJe0ye_Opgs
+https://www.youtube.com/watch?v=v3-HwZMThzQ
-Images were found at http://www.calctool.org/CALC/phys/electromagnetism/solenoid
+https://www.youtube.com/watch?v=6qrOoes_At8
 ==References==
-This section contains the the references you used while writing this page
+Matter & Interactions 4th Edition: Electric and Magnetic Interactions
+http://www.chegg.com/homework-help/questions-and-answers/x-i5rong-please-help-part-g-learning-goal-understand-processes-series-circuit-containing-i-q74127
+https://en.wikipedia.org/wiki/LC_circuit
+http://farside.ph.utexas.edu/teaching/315/Waves/node5.html
+http://physics.info/circuits-rlc/
+https://www.youtube.com/watch?v=v3-HwZMThzQ
+https://www.youtube.com/watch?v=_8d4LQMFc1o
+http://farside.ph.utexas.edu/teaching/315/Waves/node5.html
+https://www.youtube.com/watch?v=v3-HwZMThzQ
+http://www.animations.physics.unsw.edu.au/jw/LCresonance.html
 [[Category:Which Category did you place this in?]]