Newton’s Third Law of Motion: Difference between revisions
| (33 intermediate revisions by the same user not shown) | |||
| Line 2: | Line 2: | ||
Forces are products of interactions between bodies and can be defined as a interaction that has some type of effect on the motion of an object when unopposed. Forces can result by a number of contact interactions (frictional, normal, tension, applied) or just interactions between some radius (gravitational, electrical, magnetic forces). Newton's Third Law of Motion states that when there is an interaction between two objects, they are both exerting forces upon each other | Forces are products of interactions between bodies and can be defined as a interaction that has some type of effect on the motion of an object when unopposed. Forces can result by a number of contact interactions (frictional, normal, tension, applied) or just interactions between some radius (gravitational, electrical, magnetic forces). Newton's Third Law of Motion states that when there is an interaction between two objects, they are both exerting forces upon each other. These forces are examples of action-reaction pairs, which is what Newton's Third Law is entirely based around. Formally stated, Newton's third law is: '''For every action, there is an equal and opposite reaction.''' | ||
| Line 8: | Line 8: | ||
As stated above, Newton's Third Law states that if object A exerts a force on object B, then object B also exerts an equal and opposite force on object A. | As stated above, Newton's Third Law states that if object A exerts a force on object B, then object B also exerts an equal and opposite force on object A. | ||
Since the forces are considered to be interactions between multiple bodies, the forces happen in pairs. This means that there cannot only be one force being exerted on a body. In this pair, FA is called the "action" force and FB is the "reaction" force (it does not actually matter which one is the action or reaction). Since these actions occur at the same time it can be said that it is impossible for one force to exist without the other because the interaction occurs as a system. These forces are equal in magnitude and opposite in direction. | |||
===A Mathematical Model=== | ===A Mathematical Model=== | ||
Using the system of A and B, we can say that the force of A on B is equal and opposite to that of B on A. | Using the system of A and B, we can say that the force of A on B is equal and opposite to that of B on A. | ||
F(AB) = −F(BA) | |||
[[File:law3_f1.gif]] | [[File:law3_f1.gif]] | ||
= | This picture helps us to visualize what an action-reaction pair may look like in a real-life situation. The mathematical model is incredibly simple. It can be manipulated so that | ||
F(AB) + F(BA) = 0 | |||
Or in other words, the two equal and opposite forces cancel each other out. | |||
==Examples== | ==Examples== | ||
| Line 28: | Line 28: | ||
===Elementary Example=== | ===Elementary Example=== | ||
If an 100 kg person is standing stationary on the floor, what is force of the floor on the person? | |||
Solution: by Newton's Third Law, we know that for each action, there is an equal and opposite reaction. This is Newton's Third Law in its simplest form. We have a force of 980 N that the person is exerting on the floor due to their weight (Mass * acceleration of gravity). Knowing this fact, we also know that the magnitude of the force of the floor on the person is 980 N in the opposite direction. | |||
===Intermediate Example=== | ===Intermediate Example=== | ||
| Line 36: | Line 36: | ||
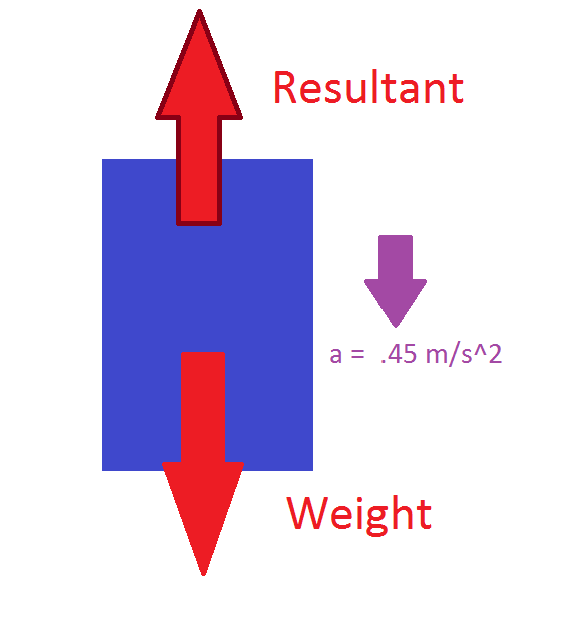
An 85 kg person is standing inside of an elevator that is accelerating at downwards at 0.45 m/s^2. Calculate the force the person exerts on the floor of the elevator. | An 85 kg person is standing inside of an elevator that is accelerating at downwards at 0.45 m/s^2. Calculate the force the person exerts on the floor of the elevator. | ||
[[File: | [[File:examplefbd.png]] | ||
We see Newton's Third Law in this example in that there is a action and reaction pair force between the floor and the person. The reaction force points upwards, opposite the direction of the force of the 85 kg person's weight. | We see Newton's Third Law in this example in that there is a action and reaction pair force between the floor and the person. The reaction force points upwards, opposite the direction of the force of the 85 kg person's weight. | ||
We can then invoke Newton's Second Law [http://physicsbook.gatech.edu/Newton%E2%80%99s_Second_Law_of_Motion]. | We can then invoke Newton's Second Law [http://physicsbook.gatech.edu/Newton%E2%80%99s_Second_Law_of_Motion]. | ||
F = ma | F = ma | ||
W - R = ma = 85 kg x 0.45 m/s^2 | W - R = ma = 85 kg x 0.45 m/s^2 | ||
R = W - 85 kg x 0.45 m/s^2 | R = W - 85 kg x 0.45 m/s^2 | ||
R = 85 kg × 9.81 m/s^2 − 85 kg × 0.45 m/s^2 = 795.6 N | R = 85 kg × 9.81 m/s^2 − 85 kg × 0.45 m/s^2 = 795.6 N | ||
| Line 47: | Line 47: | ||
===Advanced Example=== | ===Advanced Example=== | ||
(Credit to webassign.net [http://www.webassign.net/question_assets/buelemphys1/chapter06/section06dash3.pdf]for this example linking forces to momentum and energy) | |||
One implication of Newton's Third Law is the Law of Conservation of Momentum. Two carts, cart 1 and cart 2, collide with one another on a track. How does the momentum of each cart change as they collide and after the collision, what happens to the momentum of the two-cart system? The upward normal force applied by the track on each cart is balanced by the downward force of gravity, so the '''net force experienced by each cart during the collision is that applied by the other cart.''' | |||
In order to solve a collision problem, always remember that the Law of Conservation of Momentum applies. | |||
deltap2 = | The final momentum of cart 1: | ||
p1i to p1f = p1i + deltap1 (1) | |||
The final momentum of cart 2: | |||
p2i to p2f = p2i + deltap2 (2) | |||
The total initial momentum: | |||
p1i + p2i = ptotal (3) | |||
The total final momentum: | |||
p1f + p2f = p1i + deltap1 + p2i + deltap2 (4) | |||
You can verify that equation 3 and 4 are equal by plugging in arbitrary numbers--continue reading for an explanation. | |||
p1f + p2f = p1i + p2i | Consider deltap1--This change in momentum comes from the force applied to cart 1 by cart 2 during the collision. | ||
Similarly, deltap2 comes from the force applied to cart 2 by cart 1 during the collision. '''By Newton's Third Law, we know that the force applied to cart 1 by cart 2 is equal and opposite to that applied to cart 2 by cart 1.''' | |||
deltap2 = -deltap1 (Doesn't this look similar to something we already know? Hint: FAB = -FBA) | |||
The expression for total momentum of the system after the collision shows that '''momentum is conserved''' (aka momentum remains constant): | |||
p1f + p2f = p1i + p2i | |||
==Connectedness== | ==Connectedness== | ||
'''How is this topic connected to something that you are interested in?''' | '''How is this topic connected to something that you are interested in?''' | ||
Newton's Third Law is integral to understanding motion and why it occurs a certain way. | |||
Newton's Third Law is integral to understanding motion and why it occurs a certain way. In soccer, understanding why this law works the way it does helps in performance during matches and practices. From Newton’s first law, it is known that the soccer ball’s motion could not have changed unless a force acted on it--i.e. an interaction is required to produce a force. Every time a soccer ball is kicked, or involved in any contact at all, Newton's Third Law comes into play. A force from the foot is exerted onto the ball--this force is called an action force. The ball simultaneously exerts a force on your foot as it is in contact with it. This force is called a reaction force. Humans can be considered to be more massive to the ball so it is hard to realize that the soccer ball does produce a reaction force against the foot kicking it. | |||
[[File:653_Soccer_-_Newton_s_laws_of_motion_plate1.jpg]] | [[File:653_Soccer_-_Newton_s_laws_of_motion_plate1.jpg]] | ||
'''How is it connected to your major?''' | '''How is it connected to your major?''' | ||
Industrial and systems engineering has a focus on optimization of systems processes and increasing overall efficiency. Industrial engineers work to decrease or eliminate altogether the waste of time, money, materials, labor, operation times, energy and other resources that hinder the ability to generate value. According to the Institute of Industrial and Systems Engineers (IISE), at the basic level, their job is to figure out how they can do better. By engineering processes and new systems that help increase productivity, they also also able to generate a greater value than before. Having noted this, there is a physics behind productivity, especially in manufacturing firms where any extra force or motion of a machine can be holding back greater efficiency of production as a whole. | |||
[[File:industrial.PNG]] | |||
==History== | ==History== | ||
In | In the ''Principia Mathematica Philosophiae Naturalis'', Isaac Newton presented his three laws of motion (1686). Newton's three laws of motion are integral to understanding why forces have the effect they do upon other bodies. Newton's exact statement of his third law in the Principia says "To every action there is always opposed an equal reaction; or the mutual actions of the two bodies upon each other are always equal, and directed to contrary parts", which we better know as "for every action, there is an equal and opposite reaction." | ||
Proceeding this statement, Newton backs up his declaration with a few simple examples--they include the forces of a finger on a stone and the stone on the finger (see the elementary example above), the forces between a horse and a stone (connected by a rope i.e. tension force), the forces between two colliding bodies (see the advanced example above), and 'attractions' between objects, such as the force of gravity, which act at a distance. | |||
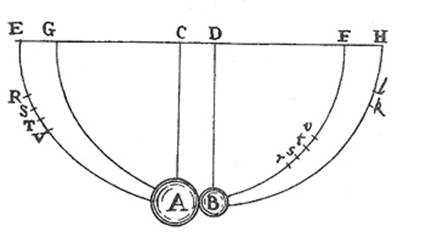
One example from Newton's Principia in order to experiment with the third law of motion was the pendulum problem. | |||
[[File:pendulumnewton.jpg]] | |||
As shown is his original diagram, Newton essentially collided together two objects of different masses in order to establish that the interactions between the two objects were equal and opposite forces. | |||
== See also == | == See also == | ||
The following links are for furthering understanding of Newton's Third Law and also practice examples. | The following links are for furthering your understanding of Newton's Third Law and also practice examples. | ||
===Additional reading=== | ===Additional reading=== | ||
| Line 108: | Line 120: | ||
[http://www.webassign.net/question_assets/buelemphys1/chapter06/section06dash3.pdf] | [http://www.webassign.net/question_assets/buelemphys1/chapter06/section06dash3.pdf] | ||
[http://physics.unipune.ernet.in/~phyed/27.2/somnathdatta.pdf] | [http://physics.unipune.ernet.in/~phyed/27.2/somnathdatta.pdf] | ||
[http://www.physicsclassroom.com/class/newtlaws/Lesson-4/Newton-s-Third-Law] | [http://www.physicsclassroom.com/class/newtlaws/Lesson-4/Newton-s-Third-Law] | ||
[http://www.webassign.net/question_assets/buelemphys1/chapter03/section03dash5.pdf] | [http://www.webassign.net/question_assets/buelemphys1/chapter03/section03dash5.pdf] | ||
[https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=9&ved=0ahUKEwjE-PSOxInMAhWBeCYKHTW0BroQFghJMAg&url=http%3A%2F%2Fconnect.issaquah.wednet.edu%2Fcfs-file.ashx%2F__key%2Ftelligent-evolution-components-attachments%2F13-12750-00-00-00-25-44-32%2FNewton_2700_s-3rd-Law-Lab.pdf&usg=AFQjCNG-sqVOgI6-ZWu115YtPPrKbGp49A&sig2=xA_w09zRYk8M74JGy-Zmug&bvm=bv.119028448,d.eWE&cad=rja] | [https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=9&ved=0ahUKEwjE-PSOxInMAhWBeCYKHTW0BroQFghJMAg&url=http%3A%2F%2Fconnect.issaquah.wednet.edu%2Fcfs-file.ashx%2F__key%2Ftelligent-evolution-components-attachments%2F13-12750-00-00-00-25-44-32%2FNewton_2700_s-3rd-Law-Lab.pdf&usg=AFQjCNG-sqVOgI6-ZWu115YtPPrKbGp49A&sig2=xA_w09zRYk8M74JGy-Zmug&bvm=bv.119028448,d.eWE&cad=rja] | ||
[[Category: | [[Category: Collisions]] | ||
Latest revision as of 17:32, 15 April 2016
Claimed by Arohi Bhakhri
Forces are products of interactions between bodies and can be defined as a interaction that has some type of effect on the motion of an object when unopposed. Forces can result by a number of contact interactions (frictional, normal, tension, applied) or just interactions between some radius (gravitational, electrical, magnetic forces). Newton's Third Law of Motion states that when there is an interaction between two objects, they are both exerting forces upon each other. These forces are examples of action-reaction pairs, which is what Newton's Third Law is entirely based around. Formally stated, Newton's third law is: For every action, there is an equal and opposite reaction.
The Main Idea
As stated above, Newton's Third Law states that if object A exerts a force on object B, then object B also exerts an equal and opposite force on object A.
Since the forces are considered to be interactions between multiple bodies, the forces happen in pairs. This means that there cannot only be one force being exerted on a body. In this pair, FA is called the "action" force and FB is the "reaction" force (it does not actually matter which one is the action or reaction). Since these actions occur at the same time it can be said that it is impossible for one force to exist without the other because the interaction occurs as a system. These forces are equal in magnitude and opposite in direction.
A Mathematical Model
Using the system of A and B, we can say that the force of A on B is equal and opposite to that of B on A.
F(AB) = −F(BA)
This picture helps us to visualize what an action-reaction pair may look like in a real-life situation. The mathematical model is incredibly simple. It can be manipulated so that
F(AB) + F(BA) = 0
Or in other words, the two equal and opposite forces cancel each other out.
Examples
Elementary Example
If an 100 kg person is standing stationary on the floor, what is force of the floor on the person?
Solution: by Newton's Third Law, we know that for each action, there is an equal and opposite reaction. This is Newton's Third Law in its simplest form. We have a force of 980 N that the person is exerting on the floor due to their weight (Mass * acceleration of gravity). Knowing this fact, we also know that the magnitude of the force of the floor on the person is 980 N in the opposite direction.
Intermediate Example
An 85 kg person is standing inside of an elevator that is accelerating at downwards at 0.45 m/s^2. Calculate the force the person exerts on the floor of the elevator.
We see Newton's Third Law in this example in that there is a action and reaction pair force between the floor and the person. The reaction force points upwards, opposite the direction of the force of the 85 kg person's weight. We can then invoke Newton's Second Law [1].
F = ma W - R = ma = 85 kg x 0.45 m/s^2 R = W - 85 kg x 0.45 m/s^2 R = 85 kg × 9.81 m/s^2 − 85 kg × 0.45 m/s^2 = 795.6 N
Advanced Example
(Credit to webassign.net [2]for this example linking forces to momentum and energy)
One implication of Newton's Third Law is the Law of Conservation of Momentum. Two carts, cart 1 and cart 2, collide with one another on a track. How does the momentum of each cart change as they collide and after the collision, what happens to the momentum of the two-cart system? The upward normal force applied by the track on each cart is balanced by the downward force of gravity, so the net force experienced by each cart during the collision is that applied by the other cart.
In order to solve a collision problem, always remember that the Law of Conservation of Momentum applies.
The final momentum of cart 1:
p1i to p1f = p1i + deltap1 (1)
The final momentum of cart 2:
p2i to p2f = p2i + deltap2 (2)
The total initial momentum:
p1i + p2i = ptotal (3)
The total final momentum:
p1f + p2f = p1i + deltap1 + p2i + deltap2 (4)
You can verify that equation 3 and 4 are equal by plugging in arbitrary numbers--continue reading for an explanation.
Consider deltap1--This change in momentum comes from the force applied to cart 1 by cart 2 during the collision. Similarly, deltap2 comes from the force applied to cart 2 by cart 1 during the collision. By Newton's Third Law, we know that the force applied to cart 1 by cart 2 is equal and opposite to that applied to cart 2 by cart 1.
deltap2 = -deltap1 (Doesn't this look similar to something we already know? Hint: FAB = -FBA)
The expression for total momentum of the system after the collision shows that momentum is conserved (aka momentum remains constant):
p1f + p2f = p1i + p2i
Connectedness
How is this topic connected to something that you are interested in?
Newton's Third Law is integral to understanding motion and why it occurs a certain way. In soccer, understanding why this law works the way it does helps in performance during matches and practices. From Newton’s first law, it is known that the soccer ball’s motion could not have changed unless a force acted on it--i.e. an interaction is required to produce a force. Every time a soccer ball is kicked, or involved in any contact at all, Newton's Third Law comes into play. A force from the foot is exerted onto the ball--this force is called an action force. The ball simultaneously exerts a force on your foot as it is in contact with it. This force is called a reaction force. Humans can be considered to be more massive to the ball so it is hard to realize that the soccer ball does produce a reaction force against the foot kicking it.
How is it connected to your major?
Industrial and systems engineering has a focus on optimization of systems processes and increasing overall efficiency. Industrial engineers work to decrease or eliminate altogether the waste of time, money, materials, labor, operation times, energy and other resources that hinder the ability to generate value. According to the Institute of Industrial and Systems Engineers (IISE), at the basic level, their job is to figure out how they can do better. By engineering processes and new systems that help increase productivity, they also also able to generate a greater value than before. Having noted this, there is a physics behind productivity, especially in manufacturing firms where any extra force or motion of a machine can be holding back greater efficiency of production as a whole.
History
In the Principia Mathematica Philosophiae Naturalis, Isaac Newton presented his three laws of motion (1686). Newton's three laws of motion are integral to understanding why forces have the effect they do upon other bodies. Newton's exact statement of his third law in the Principia says "To every action there is always opposed an equal reaction; or the mutual actions of the two bodies upon each other are always equal, and directed to contrary parts", which we better know as "for every action, there is an equal and opposite reaction."
Proceeding this statement, Newton backs up his declaration with a few simple examples--they include the forces of a finger on a stone and the stone on the finger (see the elementary example above), the forces between a horse and a stone (connected by a rope i.e. tension force), the forces between two colliding bodies (see the advanced example above), and 'attractions' between objects, such as the force of gravity, which act at a distance.
One example from Newton's Principia in order to experiment with the third law of motion was the pendulum problem.
As shown is his original diagram, Newton essentially collided together two objects of different masses in order to establish that the interactions between the two objects were equal and opposite forces.
See also
The following links are for furthering your understanding of Newton's Third Law and also practice examples.
Additional reading
Read Newton's Principia Here --> [3]
The Physics Classroom on Newton's Third Law --> [4]
External links
Watch the Best Film on Newton's Third Law. Ever. (video) --> [5]
Experiment with Newton's Third Law with these easy demos --> [6]
Newton's Third Law is just rocket science (video) --> [7]