Free Body Diagram: Difference between revisions
No edit summary |
|||
| (114 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
==Main Idea== | |||
A free body diagram, or force diagram, is a rough sketch that shows the relative magnitude and direction of all the forces acting on a system. There are various forces that can be acting on the object, such as applied force, frictional force, normal force, and gravitational force. A free body diagram allows for analysis in a steady state condition, where there can be no acceleration or a constant acceleration on a system. | |||
[[File:FBDIntroductoryImage.jpg|center|400px|An Example Sketch and Free Body Diagram]] | |||
All forces in a free body diagram are due to the system's interactions with its surroundings. Especially when problems become complicated and involve different forces acting on multiple objects, free body diagrams can be extremely effective in making problems simpler to handle. Using a free body diagram, one can solve for an unknown force acting on the body or the net acceleration after identifying all of the forces acting on it. | |||
=== | ===Mathematical Model=== | ||
Since a free body diagram is a snapshot of a steady state, there is no net acceleration or a constant net acceleration when we are modeling a free body diagram. Therefore, we can use Newton's First Law (an object in an inertial frame at rest or moving with constant velocity, will continue to do so until acted upon by a net force), Newton's Second Law (the net force on an object is equivalent to the object's mass multiplied by its net acceleration) and Newton's Third Law (for every force there is an equal and opposite reactionary force) to create a system of equations to describe and gain new information about the steady state: | |||
<math>\mathbf{F_{net}} = \sum \mathbf{F} = m \mathbf{a} = m \frac{d\mathbf{v}}{dt} </math> ('''Newton's Second Law''') | |||
Additionally, if the net acceleration is equivalent to 0, which means the object is either at rest or moving with constant velocity, then: | |||
<math>\mathbf{F_{net}} = \sum \mathbf{F} = m \mathbf{a} = m \frac{d\mathbf{v}}{dt} = \mathbf{0} </math> ('''Newton's First Law''') | |||
Also, if it is known the net acceleration is '''0''' or one or more components of the net acceleration are 0, for example a<sub>x</sub> and a<sub>y</sub>, then the components of the forces along those directions must be balanced. ('''Newton's First and Third Laws''') | |||
Using these strategies, a large set of force related problems can be solved. | |||
===Computational Model=== | |||
The following is a VPython model of the acceleration of a box as it moves down an inclined plane with negligible friction. The box starts at the top of the inclined plane, which is given by <math>pos = (5,5,5)</math>, as shown by the accompanying diagram. | |||
IMPORT STATEMENTS | |||
<code> | |||
from __future__ import division | |||
from visual import * | |||
import math | |||
</code> | |||
INITIAL CONDITIONS | |||
<code> | |||
scene.width = 1024 | |||
scene.height = 760 | |||
time = 0 #Time in seconds | |||
dtime = .1 #The time will be iterated through every .1 seconds | |||
init_pos = vector(0, 5, 5) #The initial position is at (x, y, z) = (0, 5, 5) meters | |||
init_vel = vector(0, 0, 0) #The intial velocity is (0, 0, 0) | |||
cube = box(pos = init_pos, length = 1, height = 1, width = 1) #Create a cube at the initial position | |||
mass_cube = 10 #The mass of the cube is 10 kg | |||
theta = 45 #The angle between the horizontal and the hypotneuse of the inclined plane is 45 degrees | |||
force_gravity = mass_cube * 9.81 #Force of gravity on the cube in Newtons | |||
thetaRads = math.radians(theta) #Convert degrees to radians | |||
force_normal = force_gravity * math.cos(thetaRads)#Newton's First and Second Laws #The x-axis is chosen to be along the hypotenuse of the inclined plane, and the y-axis is chosen to be along the normal to the hypotenuse. | |||
F_y = force_normal - force_gravity * math.cos(thetaRads) #This is equal to 0 | |||
F_x = force_gravity * math.sin(thetaRads) #The only force acting along the chosen x-axis is the component of the gravitational force parallel to the hypotenuse | |||
a_x = F_x / mass_cube | |||
</code> | |||
ITERATE THROUGH TIME TO FOLLOW THE MOVEMENT OF THE CUBE DOWN THE INCLINED PLANE | |||
<code> | |||
while cube.pos.x < 5: | |||
rate(200) | |||
velocity = vector(init_vel.x + (dtime * a_x), init_vel.y, init_vel.z) | |||
position = vector(cube.pos.x + (dtime * velocity.x), cube.pos.y + (dtime * velocity.y), cube.pos.z + (dtime * velocity.z)) | |||
cube.pos = position | |||
trail.append(pos = cube.pos) | |||
time = time + dtime | |||
print(cube.pos) | |||
</code> | |||
=== How To Draw a Free Body Diagram === | === How To Draw a Free Body Diagram === | ||
' | ==== Establish a Convenient Coordinate System ==== | ||
Before beginning to analyze a system, it is important to choose an appropriate coordinate system (an x and y plane) that will be the most convenient to avoid dealing with complicated angles of forces and difficult algebra and trigonometry. This is especially true when dealing with angled forces where tilting the x and y plane could make solving for resulting forces a lot easier, such as on an inclined plane. Also, in order to maintain consistency with direction amongst various people solving the same system, an x-y coordinate system can ensure that anyone solving the same system will end up with the same directions on their forces. | |||
[[File:Angled Axis.png|right|This is an example of how establishing a coordinate system can make solving/identifying forces easier]] | |||
==== Identify the System ==== | |||
Often times, you will be faced with single and multi particle systems where bodies within that system will be interacting with/exerting forces on each other. For example, a block is resting on top of a larger block, and both are moving down a ramp. In that case, analyzing the top block versus the bottom block will result in different free body diagrams. Therefore, identifying which part of the system you are analyzing before beginning to draw a free body diagram will allow for a more efficient solving process. | |||
==== List and identify all surroundings that interact with the system ==== | |||
Although we usually think of these interactions in terms of force names, it's best to get in the habit of identifying the force AND the object that specifically causes that force. For example, the force of gravity on a block could be caused by the earth or a normal force could be caused by a second block and another normal force could be caused by the table. Identifying forces by the specific objects that cause them helps us not forget where the forces belong. | |||
=====Types of Forces to Consider for Free Body Diagrams===== | |||
Disclaimer: Not all of these forces will be present in every situation. These are not all possible | '''Disclaimer: Not all of these forces will be present in every situation. These are not all of the possible forces; These are very common ones.''' | ||
*Applied Force: Force applied to the system by a person or other object. | *'''Applied Force''': | ||
*Force of Friction: Force that a surface applies on the system that is moving (or trying to move) on that surface. | **Symbol: <math style="inline">\mathbf{F_A}</math> | ||
**Formula: | **Force applied to the system by a person or other object. | ||
* | *'''Force of Friction''': | ||
**N = Normal Force | **Symbol: <math>\mathbf{F_f}</math> | ||
** | **Force that a surface applies on the system that is moving (or trying to move) on that surface. | ||
*Force of Gravity: Force that, on Earth, will act downward toward the center of the Earth. | **Formula: <math>\mathbf{F_{f}} = \mu \mathbf{N}</math> | ||
**Formula: ' | ***<math>\mathbf{N} =</math> Normal Force | ||
**m = | ***<math>\mu =</math> Coefficient of Friction | ||
**g = 9.8 m/s^2 (on earth) | *'''Force of Gravity''': | ||
*Normal | **Symbol: <math>\mathbf{F_g}</math> | ||
*Spring | **Force that, on Earth, will act downward toward the center of the Earth. In general, gravity is the attraction of any mass to any other mass. | ||
**Formula: | **Formula: <math>\mathbf{F_g} = \frac{G M_1 M_2}{r^2}{\hat{\mathbf{r}}}</math> | ||
**k = | ***This can be shown to be equal to <math>m\mathbf{g}</math> near the Earth's surface. | ||
**x = | ***<math>G = 6.7 \times 10^{-11}\ \frac{Nm^2}{{kg}^2}</math> (Gravitational Constant) | ||
*Force of | ***<math>M_1 =</math> Mass 1 | ||
***<math>M_2 =</math> Mass 2 | |||
***<math>r =</math> Displacement between Masses 1 and 2 | |||
***<math>{\hat{\mathbf{r}}} =</math> Unit vector in direction of Displacement between the Masses | |||
***<math>m =</math> Mass of object on Earth | |||
***<math>\mathbf{g} = 9.8\ m/s^2 </math> (on earth) | |||
*'''Normal Force''': | |||
**Symbol: <math>\mathbf{F_N}</math> | |||
**Force that is present when the system is on another object or surface, and the object or surface is exerting a force on the system as support. | |||
*'''Spring Force''' | |||
**Symbol: <math>\mathbf{F_s}</math> | |||
**Force that is exerted by a spring on any system that is attached to it. | |||
**Formula: <math>\mathbf{F_s} = -k\mathbf{x}</math> (Hookian Spring) | |||
***<math>k =</math> Spring constant (<math>\ \frac{N}{m}</math>) | |||
***<math>\mathbf{x} =</math> Displacement from the spring's equilibrium position | |||
*'''Force of Tension''': | |||
**Symbol: <math>\mathbf{F_T}</math> or <math>\mathbf{T}</math> | |||
**Force that exists when a rope, string, wire, etc. is pulling on the system. | |||
'''Side Note:''' | |||
* | Now that we've touched on frictional forces, it is important to understand the types of frictional forces. Frictional forces include two types: static friction and dynamic (kinetic) friction. These two types of friction have different coefficients of friction, usually represented by <math>\mu_s</math> for static friction and <math>\mu_k</math> for dynamic (kinetic friction. | ||
*'''Static Friction''' refers to the frictional force while the object is stationary. An external net force higher than this static frictional force is required to move the object. | |||
*'''Dynamic (Kinetic) Friction''' refers to the frictional force while the object is in motion. For example, the object may experience a frictional force with the ground while it is moving along the ground. | |||
==== | ==== Draw a diagram with the system at the center ==== | ||
( | #Use a dot to represent the system, OR | ||
#You can draw the details of the system (Draw a block, car, etc.) | |||
#Draw the conveniently oriented coordinate system on the free body diagram or next to the it | |||
#Draw the system's relevant force vectors with correct relative magnitude and direction, pointing away from the dot or detailed drawing | |||
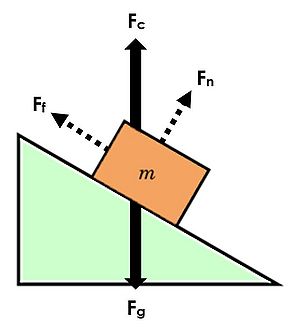
[[File:ContactForce.JPG|300px|thumb|right|]] | [[File:ContactForce.JPG|300px|thumb|right|]] | ||
==== | ==== Label all Forces With a Symbol ==== | ||
Symbols are useful to quickly represent the name of the force and identify them by the object causing the force. Refer to [[#Types of Forces to Consider for Free Body Diagrams| Common Symbols for Forces]]. | |||
==== Break forces into their components as needed. ==== | |||
If a force is acting diagonal to the system, create a dashed line parallel and perpendicular to the system and label it as the x and y components of that force. Use sine(θ) or cosine(θ) as needed. | If a force is acting diagonal to the system, create a dashed line parallel and perpendicular to the system and label it as the x and y components of that force. Use sine(θ) or cosine(θ) as needed. | ||
| Line 66: | Line 155: | ||
*If an object has constant speed, it means the object has no acceleration. Since net force is the rate of change of acceleration, net force in that direction would then be zero. This means that there are either no forces currently acting on the object, or there are equal, opposite forces acting on the object in that direction. To represent this in a free body diagram, draw forces as arrows pointing in opposite directions with equal lengths. | *If an object has constant speed, it means the object has no acceleration. Since net force is the rate of change of acceleration, net force in that direction would then be zero. This means that there are either no forces currently acting on the object, or there are equal, opposite forces acting on the object in that direction. To represent this in a free body diagram, draw forces as arrows pointing in opposite directions with equal lengths. | ||
*Don't be confused by contact forces. Most of the time, contact force is an umbrella term that includes other types of forces. If you had a block on a ramp, you could draw the contact force as being diagonal to the ramp. Or, if you wanted to break it into its components which are easier to consider, you would draw the Normal force caused by the ramp pushing up as a perpendicular arrow, and the force of Friction caused by the ramp as a parallel arrow (see image to the upper right). | *Don't be confused by contact forces. Most of the time, contact force is an umbrella term that includes other types of forces. If you had a block on a ramp, you could draw the contact force as being diagonal to the ramp. Or, if you wanted to break it into its components which are easier to consider, you would draw the Normal force caused by the ramp pushing up as a perpendicular arrow, and the force of Friction caused by the ramp as a parallel arrow (see image to the upper right). | ||
==== Sum the forces ==== | |||
Once you have drawn the free body diagram and broken the forces into components along the convenient x-y axis (if needed), then it is time to use [[#Mathematical Model | Mathematical Model]] to create a system of equations summing the forces in the x and y directions and then set them equal to the correct value, such as 0 if there is no acceleration in that direction or <math>m\mathbf{a}</math>. | |||
# | |||
==Examples== | |||
In this section we will go step by step through 3 illustrative examples, increasing in difficulty as we go. | |||
=== Simple === | === Simple === | ||
A person with a mass of <math>M</math> rides up to the 20th floor of their apartment building in an elevator moving at constant velocity. Create a free body diagram to represent this situation. Using your free body diagram, use Newton's Second Law to create a force equation for the system. Make sure to keep track of the relative magnitudes of the forces and indicate these magnitudes by the length of the arrow. | |||
[[File: | |||
'''''Answer''''' | |||
We start by drawing a free body diagram with correct relative magnitudes and directions of the Normal Force and the Gravitational Force. The normal force is always normal (perpendicular or orthogonal) to the surface, whether the surface is angled or not. Gravity always acts downwards on Earth. Therefore, there is no need to create a different, convenient coordinate plane. A horizontal x-axis and vertical y-axis will suffice. These are the only two forces acting on the person because nothing else is pushing on the person, and friction is not being taken into account. We know the normal force must be present due to the person not falling through the floor (due to the always present gravitational force). We can also reason that these forces must be equal in magnitude and opposite in direction. | |||
[[File:FBDSimpleSketch.jpeg|right|400px|A Sketch]] | |||
[[File:FBDSimple.jpeg|right|200px|A Free Body Diagram]] | |||
Next, we use Newton's Second Law to begin our analysis: | |||
:<math display="block">\mathbf{F_{net}} = \sum\mathbf{F} = m\mathbf{a}</math> | |||
Next, we notice the problem states that the person moves with a constant velocity upwards, therefore there is no acceleration in any direction, and the net force must be equal to <math>\mathbf{0}</math>: | |||
:<math display="block">\mathbf{F_{net}} = \sum\mathbf{F} = m\mathbf{a} = \mathbf{0}</math> | |||
The normal force and gravitational force can be described as: | |||
:<math display="block">\mathbf{F_g} = \begin{bmatrix} |\mathbf{F_g}| \ \text{cos}(180^\text{o}) \\ |\mathbf{F_g}| \ \text{sin}(180^\text{o}) \end{bmatrix} = \begin{bmatrix} 0 \\ -|\mathbf{F_g}| \end{bmatrix}</math> | |||
:<math display="block">\mathbf{F_N} = \begin{bmatrix} |\mathbf{F_N}| \ \text{cos}(90^\text{o}) \\ |\mathbf{F_N}| \ \text{sin}(90^\text{o}) \end{bmatrix} = \begin{bmatrix} 0 \\ |\mathbf{F_N}| \end{bmatrix}</math> | |||
Next, putting the free body diagram and Newton's Second Law together gives: | |||
:<math display="block">\mathbf{F_{net}} = \sum\mathbf{F} = \begin{bmatrix} 0 \\ \mathbf{|F_N|} \end{bmatrix} + \begin{bmatrix} 0 \\ -\mathbf{|F_g|} \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix}</math> | |||
Therefore, it is possible to simplify the above to show that the gravitational force is exactly opposite in direction and equal in magnitude: | |||
:<math display="block">|\mathbf{F_g}| = |\mathbf{F_N}|</math> | |||
:<math display="block">|\mathbf{F_N}| = Mg </math> | |||
We have fully done what the problem asked. | |||
=== Middling === | === Middling === | ||
A ball with mass <math>m</math> is hanging tautly from two strings of negligible mass, each of which are connected to the ceiling. To the left of the ball, one string has a tension <math>\mathbf{T_1}</math> and makes an angle of <math>20^\text{o}</math> with the ceiling, and on the right of the ball, the other string has a tension <math>\mathbf{T_2}</math> and creates an angle of <math>45^\text{o}</math> with the ceiling. Both angles are measured from the ceiling to the inner side of the string. Refer to the diagram for any confusion. Create a free body diagram to model this situation. Also, create a system of force equations. '''Hint''': x and y components will be needed for this problem. | |||
'''''Answer''''' | |||
To draw the free body diagram it is better to first draw a sketch of the system. In the sketch we see the string to the left (<math>\mathbf{T_1}</math>) of the ball makes an angle of <math>20^\text{o}</math> with the ceiling, and the string to the right (<math>\mathbf{T_2}</math>) of the ball makes an angle <math>45^\text{o}</math> with the ceiling. For the free body diagram, we first draw the force of gravity pointing straight downwards. This force should have the longest arrow due to the fact that the strings are supporting this force...therefore, it can be reasoned that this force should be greater than either of the tensions in the strings for the given angles. Next, we draw the tension forces, which point away from the ball along each respective string. <math>\mathbf{T_2}</math> should be longer than <math>\mathbf{T_1}</math> due to the fact that the tensions must balance each other along the x-axis and the y-component of <math>\mathbf{T_2}</math> must be greater than the y-component of <math>\mathbf{T_1}</math>. | |||
[[File:FBDMiddlingSketch.jpeg|right| 400px|A Sketch]] | |||
[[File:FBDMiddling.jpeg|right|300px|A Free Body Diagram]] | |||
Now, we are ready to use Newton's First and Second Laws to create a system of force equations: | |||
:<math display="block">\mathbf{F_{net}} = \sum\mathbf{F} = m\mathbf{a}</math> | |||
Since the ball is hanging tautly, it must NOT be moving. Therefore, the velocity and acceleration must both be <math>\mathbf{0}</math>: | |||
:<math display="block">\mathbf{F_{net}} = \sum\mathbf{F} = m\mathbf{a} = \mathbf{0}</math> | |||
Next, we choose the x-axis to be horizontal, and the y-axis to be vertical, as in a typical coordinate system, since it is convenient. | |||
Now, we begin specifically identifying the forces and their components using right triangles: | |||
:<math display="block">\mathbf{F_g} = \begin{bmatrix} |\mathbf{F_g}| \ \text{cos}(180^\text{o}) \\ |\mathbf{F_g}| \ \text{sin}(180^\text{o}) \end{bmatrix} = \begin{bmatrix} 0 \\ -|\mathbf{F_g}| \end{bmatrix}</math> | |||
:<math display="block">\mathbf{T_1} = \begin{bmatrix} -|\mathbf{T_1}| \ \text{cos}(20^\text{o}) \\ |\mathbf{T_1}| \ \text{sin}(20^\text{o})\end{bmatrix} </math> | |||
:<math display="block">\mathbf{T_2} = \begin{bmatrix} -|\mathbf{T_2}| \ \text{cos}(45^\text{o}) \\ |\mathbf{T_2}| \ \text{sin}(45^\text{o})\end{bmatrix}</math> | |||
Next, we use Newton's Second Law to sum these forces. Since the ball is not moving, we can set this summation equal to <math>\mathbf{0}</math>: | |||
:<math display="block">\mathbf{F_{net}} = \sum\mathbf{F} = m\mathbf{a} = \mathbf{0} = \mathbf{F_g} + \mathbf{T_1} + \mathbf{T_2}</math> | |||
This is equivalent to: | |||
:<math display="block"> \begin{bmatrix} 0 \\ -|\mathbf{F_g}| \end{bmatrix} + \begin{bmatrix} -|\mathbf{T_1}| \ \text{cos}(20^\text{o}) \\ |\mathbf{T_1}| \ \text{sin}(20^\text{o})\end{bmatrix} + \begin{bmatrix} -|\mathbf{T_2}| \ \text{cos}(45^\text{o}) \\ |\mathbf{T_2}| \ \text{sin}(45^\text{o})\end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix}</math> | |||
Hence, we have done what the question asked and are done with this problem. | |||
=== Difficult === | === Difficult === | ||
A father pushes his son's sled horizontally with a force <math>\mathbf{F_A}</math> all the way down a hill on a sled of mass <math>M</math>. The son has a mass <math>m</math>. The son/sled system is accelerating down the hill. Assume the hill is shaped like an inclined plane with an angle to the horizontal ground of <math>35^{\text{o}}</math> and that friction works against the sled with a coefficient of dynamic (kinetic) friction <math>\mu_k</math>. Draw a free-body diagram. Using your free body diagram, write a system of equations that could be used to solve for the acceleration of the son/sled system. | |||
'''''Answer''''' | |||
We start with a sketch. In this sketch, we create an inclined plane with the the specified <math>35^{\text{o}}</math> angle, with the dad behind the kid pushing the sled down the hill. Some forces to be thinking about in this situation are the normal force, the applied force of the dad, the frictional force opposing the motion, and the gravitational force pulling the system straight down. To begin the free body diagram, we draw a circle to symbolize the son/sled system. Next, we draw the gravitational force as straight down, as it will always be in these Earth situations. Its length should be longer than the normal force. Otherwise, it shouldn't be compared to the other forces. Next are the frictional force and the normal force. The normal force should be normal to the inclined plane, and the frictional force should be parallel to the inclined plane, but opposite the direction of motion. Finally, the applied force of the dad should be parallel to the flat ground. The free body diagram has been created. Now, we must create a system of equations that could be solved for the acceleration of the son/sled system. | |||
[[File:FBDSketchDifficult.jpeg|right|400px|A Sketch]] | |||
[[File:FBDDifficult.jpeg|right|400px|A Free Body Diagram]] | |||
To begin, we draw an x-y plane, where the y-axis runs along the the normal force and the x-axis runs along the frictional force. This will simplify the representation of these two forces, as well as represent the gravitational force with just a couple trigonometric functions. The applied force will have the same done to it. | |||
Newton's Second Law states the net force on a system is equal to the mass of the system times the acceleration: | |||
:<math display="block">\mathbf{F_{net}} = \sum \mathbf{F} = m_{system}\mathbf{a}</math> | |||
We are told the son/sled system is accelerating, therefore the above equation can NOT be set equal to <math>\mathbf{0}</math>. | |||
We also know the son/sled system should have a combined mass of <math>M + m</math>, where <math>M</math> is the mass of the sled and <math>m</math> is the mass of the son, as stated in the problem: | |||
:<math display="block">\mathbf{F_{net}} = \sum \mathbf{F} = m_{system}\mathbf{a} = (M + m) \mathbf{a}</math> | |||
The angle <math>\mathbf{F_A}</math> makes with the chosen x-axis is <math>35^{\text{o}}</math>. This can be seen from the sketch. The angle the gravitational force makes with the chosen y-axis is also <math>35^{\text{o}}</math>. This can also be seen in the sketch. Therefore, the four forces considered in this system can be described as: | |||
:<math display="block">\mathbf{F_g} = \begin{bmatrix} |\mathbf{F_g}| \ \text{cos}(35^\text{o}) \\ |\mathbf{F_g}| \ \text{sin}(35^\text{o})\end{bmatrix}</math> | |||
== | :<math display="block">\mathbf{F_A} = \begin{bmatrix} |\mathbf{F_A}| \ \text{cos}(35^\text{o}) \\ |\mathbf{F_A}| \ \text{sin}(35^\text{o}) \end{bmatrix}</math> | ||
== See | :<math display="block">\mathbf{F_f} = \begin{bmatrix} |\mathbf{F_f}| \ \text{cos}(180^\text{o}) \\ |\mathbf{F_f}| \ \text{sin}(180^\text{o}) \end{bmatrix} = \begin{bmatrix} -|\mathbf{F_f}| \\ 0 \end{bmatrix}</math> | ||
:<math display="block">\mathbf{F_N} = \begin{bmatrix} |\mathbf{F_N}| \ \text{cos}(90^\text{o}) \\ |\mathbf{F_N}| \ \text{sin}(90^\text{o}) \end{bmatrix} = \begin{bmatrix} 0 \\ |\mathbf{F_N}| \end{bmatrix}</math> | |||
Using Newton's Second Law, we know that: | |||
:<math display="block">\mathbf{F_{net}} = \sum \mathbf{F} = m_{system}\mathbf{a} = (M + m) \mathbf{a} = \mathbf{F_g} + \mathbf{F_A} + \mathbf{F_f} + \mathbf{F_N}</math> | |||
This is equivalent to: | |||
:<math display="block">\mathbf{a} = \frac{\begin{bmatrix} |\mathbf{F_g}| \ \text{cos}(35^\text{o}) \\ |\mathbf{F_g}| \ \text{sin}(35^\text{o})\end{bmatrix} + \begin{bmatrix} |\mathbf{F_A}| \ \text{cos}(35^\text{o}) \\ |\mathbf{F_A}| \ \text{sin}(35^\text{o}) \end{bmatrix} + \begin{bmatrix} -|\mathbf{F_A}| \\ 0 \end{bmatrix} + \begin{bmatrix} 0 \\ |\mathbf{F_N}| \end{bmatrix}}{M+m}</math> | |||
Thus we have done what the problem asked. | |||
==Connectedness== | |||
Free body diagrams are the building blocks for many scientists, physicists, engineers and have many applications in the real world. They form the basis for determining a device's or building's structural stability, safety, and overall practicality. | |||
'''Medical Applications''' | |||
[[File:Leg.gif|right|]] | |||
There have recently been many advances in medicine in terms of wearables and prosthetic limbs that function just like normal body parts for either congenital defects or accident recovery. Let's take a look at a leg prosthetic. While walking, a prosthetic exerts many forces on your leg such as: the force of gravity, normal force from the ground, frictional force, etc. | |||
Prosthetics move like springs, while your body moves forward it also moves up and down which causes changes in kinetic energy due to movement and changes in gravitational potential energy. While it contracts and relaxes, different energies are converted back and forth into kinetic and potential energy. In order to analyze all the forces on a prosthetic to ensure it's safety and usability, the most basic step when designing one is a free body diagram. | |||
'''Buildings and Trusses''' | |||
Many civil engineers and architects are responsible for building trusses, bridges, and buildings which function using the basic concepts of physics. It is important to ensure that components of a truss and bridge are in equilibrium so that one day they don't collapse. | |||
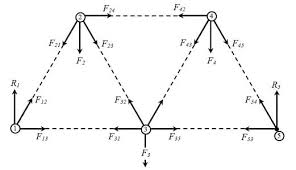
When building a truss bridge, engineers put straight members in place that form the bridge's top and bottom, and they are linked by a structure of diagonals and vertical posts. For trusses especially, all the components must remain in equilibrium, the magnitudes of forces exerted must be equal, and the components in tension and compression must be identified. In order to create a proper structure, a free body diagram must be used by engineers in the preliminary stages for design and safety purposes. | |||
[[File:Truss.gif]] | |||
==History== | |||
EDITED BY DEEPIKA RAVI, FALL 2025 | |||
Free Body Diagrams were developed alongside Newtonian physics as a graphical way to analyze what forces were acting on a system and how the system would react. More specifically, it traces its roots back to the works of Isaac Newton and later engineers who wanted to develop practical methods for applying Newton's laws. Although Newton himself did not develop the modern form of a force diagram, he developed the conceptual fondation of isolation a system and analyzing the forces acting upon it.<ref>Dugas, René. ''A History of Mechanics''. Routledge, 1955 [http://deadnet.se:8080/Books_and_manuals_on_various_stuff/Science/History%20and%20Philosophy%20of%20Science/Dugas%20-%20A%20History%20of%20Mechanics%20%28Routledge%2C%201955%29.pdf Online PDF]</ref> As physics and engineering developed rapidly through the Industrial Revolution, a systemic approach to statics and dynamics grew. Early engineering texts in the 1800s started to include sketches which showed loads on beams, tension in cables, and normal forces acting on supports. These sketches slowly became the standardized norm in engineering colleges. By the late 19th and early 20th centuries, free body diagrams became an essential problem solving tool, especially in the development of infrastructure, such as bridges. Take for example an analysis of the forces in a Truss Bridge.<ref>TeachEngineering. "Analyzing Forces in a Truss Bridge." https://www.teachengineering.org/lessons/view/ind-2472-analysis-forces-truss-bridge-lesson</ref> | |||
<div style="text-align:center;">[[File:Trussbridge.jpg|400px|Truss bridge forces]]</div> | |||
Due to their widespread usefulness, free body diagrams have not fallen out of favor with scientists and engineers. They continue to be used as a teaching and real world tool for well over a century. Free body diagrams are emphasized to be a foundational skill for students, allowing them to translate real-world systems into mathematical models. With the improvements in computer-aided models and design tools, the role of FBDs still remains essential to engineering. | |||
== References == | |||
<references/> | |||
==See Also== | |||
===Further Reading=== | |||
[[Inclined Plane]] | |||
[[Compression or Normal Force]] | |||
[[Tension]] | |||
[[Gravitational Force]] | |||
[[Spring Force]] | |||
[[Hooke's Law]] | |||
[[Net Force]] | |||
===External Links=== | |||
[http://hyperphysics.phy-astr.gsu.edu/hbase/force.html Forces Mental Map] | [http://hyperphysics.phy-astr.gsu.edu/hbase/force.html Forces Mental Map] | ||
| Line 118: | Line 330: | ||
[https://www.youtube.com/watch?v=nDis6HbXxjg Using Free-Body Diagrams to Solve Kinematics Problems] | [https://www.youtube.com/watch?v=nDis6HbXxjg Using Free-Body Diagrams to Solve Kinematics Problems] | ||
== References == | == References == | ||
| Line 131: | Line 341: | ||
http://www.physicsclassroom.com/Class/newtlaws | http://www.physicsclassroom.com/Class/newtlaws | ||
https://sites.google.com/a/cpsdigital.org/peraplegic/human-prosthetics | |||
http://slideplayer.com/slide/6086550/ - Tilted Axis Image | |||
http://www.revistas.unal.edu.co/index.php/dyna/rt/printerFriendly/30749/39025 - Prosthetic Limb Image | |||
http://www.mathalino.com/reviewer/engineering-mechanics/241-finding-resulatnt-vertical-forces-acting-fink-truss - Truss Image | |||
Latest revision as of 13:51, 2 December 2025
Main Idea
A free body diagram, or force diagram, is a rough sketch that shows the relative magnitude and direction of all the forces acting on a system. There are various forces that can be acting on the object, such as applied force, frictional force, normal force, and gravitational force. A free body diagram allows for analysis in a steady state condition, where there can be no acceleration or a constant acceleration on a system.

All forces in a free body diagram are due to the system's interactions with its surroundings. Especially when problems become complicated and involve different forces acting on multiple objects, free body diagrams can be extremely effective in making problems simpler to handle. Using a free body diagram, one can solve for an unknown force acting on the body or the net acceleration after identifying all of the forces acting on it.
Mathematical Model
Since a free body diagram is a snapshot of a steady state, there is no net acceleration or a constant net acceleration when we are modeling a free body diagram. Therefore, we can use Newton's First Law (an object in an inertial frame at rest or moving with constant velocity, will continue to do so until acted upon by a net force), Newton's Second Law (the net force on an object is equivalent to the object's mass multiplied by its net acceleration) and Newton's Third Law (for every force there is an equal and opposite reactionary force) to create a system of equations to describe and gain new information about the steady state:
[math]\displaystyle{ \mathbf{F_{net}} = \sum \mathbf{F} = m \mathbf{a} = m \frac{d\mathbf{v}}{dt} }[/math] (Newton's Second Law)
Additionally, if the net acceleration is equivalent to 0, which means the object is either at rest or moving with constant velocity, then:
[math]\displaystyle{ \mathbf{F_{net}} = \sum \mathbf{F} = m \mathbf{a} = m \frac{d\mathbf{v}}{dt} = \mathbf{0} }[/math] (Newton's First Law)
Also, if it is known the net acceleration is 0 or one or more components of the net acceleration are 0, for example ax and ay, then the components of the forces along those directions must be balanced. (Newton's First and Third Laws)
Using these strategies, a large set of force related problems can be solved.
Computational Model
The following is a VPython model of the acceleration of a box as it moves down an inclined plane with negligible friction. The box starts at the top of the inclined plane, which is given by [math]\displaystyle{ pos = (5,5,5) }[/math], as shown by the accompanying diagram.
IMPORT STATEMENTS
from __future__ import division
from visual import *
import math
INITIAL CONDITIONS
scene.width = 1024
scene.height = 760
time = 0 #Time in seconds
dtime = .1 #The time will be iterated through every .1 seconds
init_pos = vector(0, 5, 5) #The initial position is at (x, y, z) = (0, 5, 5) meters
init_vel = vector(0, 0, 0) #The intial velocity is (0, 0, 0)
cube = box(pos = init_pos, length = 1, height = 1, width = 1) #Create a cube at the initial position
mass_cube = 10 #The mass of the cube is 10 kg
theta = 45 #The angle between the horizontal and the hypotneuse of the inclined plane is 45 degrees
force_gravity = mass_cube * 9.81 #Force of gravity on the cube in Newtons
thetaRads = math.radians(theta) #Convert degrees to radians
force_normal = force_gravity * math.cos(thetaRads)#Newton's First and Second Laws #The x-axis is chosen to be along the hypotenuse of the inclined plane, and the y-axis is chosen to be along the normal to the hypotenuse.
F_y = force_normal - force_gravity * math.cos(thetaRads) #This is equal to 0
F_x = force_gravity * math.sin(thetaRads) #The only force acting along the chosen x-axis is the component of the gravitational force parallel to the hypotenuse
a_x = F_x / mass_cube
ITERATE THROUGH TIME TO FOLLOW THE MOVEMENT OF THE CUBE DOWN THE INCLINED PLANE
while cube.pos.x < 5:
rate(200)
velocity = vector(init_vel.x + (dtime * a_x), init_vel.y, init_vel.z)
position = vector(cube.pos.x + (dtime * velocity.x), cube.pos.y + (dtime * velocity.y), cube.pos.z + (dtime * velocity.z))
cube.pos = position
trail.append(pos = cube.pos)
time = time + dtime
print(cube.pos)
How To Draw a Free Body Diagram
Establish a Convenient Coordinate System
Before beginning to analyze a system, it is important to choose an appropriate coordinate system (an x and y plane) that will be the most convenient to avoid dealing with complicated angles of forces and difficult algebra and trigonometry. This is especially true when dealing with angled forces where tilting the x and y plane could make solving for resulting forces a lot easier, such as on an inclined plane. Also, in order to maintain consistency with direction amongst various people solving the same system, an x-y coordinate system can ensure that anyone solving the same system will end up with the same directions on their forces.

Identify the System
Often times, you will be faced with single and multi particle systems where bodies within that system will be interacting with/exerting forces on each other. For example, a block is resting on top of a larger block, and both are moving down a ramp. In that case, analyzing the top block versus the bottom block will result in different free body diagrams. Therefore, identifying which part of the system you are analyzing before beginning to draw a free body diagram will allow for a more efficient solving process.
List and identify all surroundings that interact with the system
Although we usually think of these interactions in terms of force names, it's best to get in the habit of identifying the force AND the object that specifically causes that force. For example, the force of gravity on a block could be caused by the earth or a normal force could be caused by a second block and another normal force could be caused by the table. Identifying forces by the specific objects that cause them helps us not forget where the forces belong.
Types of Forces to Consider for Free Body Diagrams
Disclaimer: Not all of these forces will be present in every situation. These are not all of the possible forces; These are very common ones.
- Applied Force:
- Symbol: [math]\displaystyle{ \mathbf{F_A} }[/math]
- Force applied to the system by a person or other object.
- Force of Friction:
- Symbol: [math]\displaystyle{ \mathbf{F_f} }[/math]
- Force that a surface applies on the system that is moving (or trying to move) on that surface.
- Formula: [math]\displaystyle{ \mathbf{F_{f}} = \mu \mathbf{N} }[/math]
- [math]\displaystyle{ \mathbf{N} = }[/math] Normal Force
- [math]\displaystyle{ \mu = }[/math] Coefficient of Friction
- Force of Gravity:
- Symbol: [math]\displaystyle{ \mathbf{F_g} }[/math]
- Force that, on Earth, will act downward toward the center of the Earth. In general, gravity is the attraction of any mass to any other mass.
- Formula: [math]\displaystyle{ \mathbf{F_g} = \frac{G M_1 M_2}{r^2}{\hat{\mathbf{r}}} }[/math]
- This can be shown to be equal to [math]\displaystyle{ m\mathbf{g} }[/math] near the Earth's surface.
- [math]\displaystyle{ G = 6.7 \times 10^{-11}\ \frac{Nm^2}{{kg}^2} }[/math] (Gravitational Constant)
- [math]\displaystyle{ M_1 = }[/math] Mass 1
- [math]\displaystyle{ M_2 = }[/math] Mass 2
- [math]\displaystyle{ r = }[/math] Displacement between Masses 1 and 2
- [math]\displaystyle{ {\hat{\mathbf{r}}} = }[/math] Unit vector in direction of Displacement between the Masses
- [math]\displaystyle{ m = }[/math] Mass of object on Earth
- [math]\displaystyle{ \mathbf{g} = 9.8\ m/s^2 }[/math] (on earth)
- Normal Force:
- Symbol: [math]\displaystyle{ \mathbf{F_N} }[/math]
- Force that is present when the system is on another object or surface, and the object or surface is exerting a force on the system as support.
- Spring Force
- Symbol: [math]\displaystyle{ \mathbf{F_s} }[/math]
- Force that is exerted by a spring on any system that is attached to it.
- Formula: [math]\displaystyle{ \mathbf{F_s} = -k\mathbf{x} }[/math] (Hookian Spring)
- [math]\displaystyle{ k = }[/math] Spring constant ([math]\displaystyle{ \ \frac{N}{m} }[/math])
- [math]\displaystyle{ \mathbf{x} = }[/math] Displacement from the spring's equilibrium position
- Force of Tension:
- Symbol: [math]\displaystyle{ \mathbf{F_T} }[/math] or [math]\displaystyle{ \mathbf{T} }[/math]
- Force that exists when a rope, string, wire, etc. is pulling on the system.
Side Note: Now that we've touched on frictional forces, it is important to understand the types of frictional forces. Frictional forces include two types: static friction and dynamic (kinetic) friction. These two types of friction have different coefficients of friction, usually represented by [math]\displaystyle{ \mu_s }[/math] for static friction and [math]\displaystyle{ \mu_k }[/math] for dynamic (kinetic friction.
- Static Friction refers to the frictional force while the object is stationary. An external net force higher than this static frictional force is required to move the object.
- Dynamic (Kinetic) Friction refers to the frictional force while the object is in motion. For example, the object may experience a frictional force with the ground while it is moving along the ground.
Draw a diagram with the system at the center
- Use a dot to represent the system, OR
- You can draw the details of the system (Draw a block, car, etc.)
- Draw the conveniently oriented coordinate system on the free body diagram or next to the it
- Draw the system's relevant force vectors with correct relative magnitude and direction, pointing away from the dot or detailed drawing
Label all Forces With a Symbol
Symbols are useful to quickly represent the name of the force and identify them by the object causing the force. Refer to Common Symbols for Forces.
Break forces into their components as needed.
If a force is acting diagonal to the system, create a dashed line parallel and perpendicular to the system and label it as the x and y components of that force. Use sine(θ) or cosine(θ) as needed.
General Tips:
- If an object has constant speed, it means the object has no acceleration. Since net force is the rate of change of acceleration, net force in that direction would then be zero. This means that there are either no forces currently acting on the object, or there are equal, opposite forces acting on the object in that direction. To represent this in a free body diagram, draw forces as arrows pointing in opposite directions with equal lengths.
- Don't be confused by contact forces. Most of the time, contact force is an umbrella term that includes other types of forces. If you had a block on a ramp, you could draw the contact force as being diagonal to the ramp. Or, if you wanted to break it into its components which are easier to consider, you would draw the Normal force caused by the ramp pushing up as a perpendicular arrow, and the force of Friction caused by the ramp as a parallel arrow (see image to the upper right).
Sum the forces
Once you have drawn the free body diagram and broken the forces into components along the convenient x-y axis (if needed), then it is time to use Mathematical Model to create a system of equations summing the forces in the x and y directions and then set them equal to the correct value, such as 0 if there is no acceleration in that direction or [math]\displaystyle{ m\mathbf{a} }[/math].
Examples
In this section we will go step by step through 3 illustrative examples, increasing in difficulty as we go.
Simple
A person with a mass of [math]\displaystyle{ M }[/math] rides up to the 20th floor of their apartment building in an elevator moving at constant velocity. Create a free body diagram to represent this situation. Using your free body diagram, use Newton's Second Law to create a force equation for the system. Make sure to keep track of the relative magnitudes of the forces and indicate these magnitudes by the length of the arrow.
Answer
We start by drawing a free body diagram with correct relative magnitudes and directions of the Normal Force and the Gravitational Force. The normal force is always normal (perpendicular or orthogonal) to the surface, whether the surface is angled or not. Gravity always acts downwards on Earth. Therefore, there is no need to create a different, convenient coordinate plane. A horizontal x-axis and vertical y-axis will suffice. These are the only two forces acting on the person because nothing else is pushing on the person, and friction is not being taken into account. We know the normal force must be present due to the person not falling through the floor (due to the always present gravitational force). We can also reason that these forces must be equal in magnitude and opposite in direction.


Next, we use Newton's Second Law to begin our analysis:
- [math]\displaystyle{ \mathbf{F_{net}} = \sum\mathbf{F} = m\mathbf{a} }[/math]
Next, we notice the problem states that the person moves with a constant velocity upwards, therefore there is no acceleration in any direction, and the net force must be equal to [math]\displaystyle{ \mathbf{0} }[/math]:
- [math]\displaystyle{ \mathbf{F_{net}} = \sum\mathbf{F} = m\mathbf{a} = \mathbf{0} }[/math]
The normal force and gravitational force can be described as:
- [math]\displaystyle{ \mathbf{F_g} = \begin{bmatrix} |\mathbf{F_g}| \ \text{cos}(180^\text{o}) \\ |\mathbf{F_g}| \ \text{sin}(180^\text{o}) \end{bmatrix} = \begin{bmatrix} 0 \\ -|\mathbf{F_g}| \end{bmatrix} }[/math]
- [math]\displaystyle{ \mathbf{F_N} = \begin{bmatrix} |\mathbf{F_N}| \ \text{cos}(90^\text{o}) \\ |\mathbf{F_N}| \ \text{sin}(90^\text{o}) \end{bmatrix} = \begin{bmatrix} 0 \\ |\mathbf{F_N}| \end{bmatrix} }[/math]
Next, putting the free body diagram and Newton's Second Law together gives:
- [math]\displaystyle{ \mathbf{F_{net}} = \sum\mathbf{F} = \begin{bmatrix} 0 \\ \mathbf{|F_N|} \end{bmatrix} + \begin{bmatrix} 0 \\ -\mathbf{|F_g|} \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} }[/math]
Therefore, it is possible to simplify the above to show that the gravitational force is exactly opposite in direction and equal in magnitude:
- [math]\displaystyle{ |\mathbf{F_g}| = |\mathbf{F_N}| }[/math]
- [math]\displaystyle{ |\mathbf{F_N}| = Mg }[/math]
We have fully done what the problem asked.
Middling
A ball with mass [math]\displaystyle{ m }[/math] is hanging tautly from two strings of negligible mass, each of which are connected to the ceiling. To the left of the ball, one string has a tension [math]\displaystyle{ \mathbf{T_1} }[/math] and makes an angle of [math]\displaystyle{ 20^\text{o} }[/math] with the ceiling, and on the right of the ball, the other string has a tension [math]\displaystyle{ \mathbf{T_2} }[/math] and creates an angle of [math]\displaystyle{ 45^\text{o} }[/math] with the ceiling. Both angles are measured from the ceiling to the inner side of the string. Refer to the diagram for any confusion. Create a free body diagram to model this situation. Also, create a system of force equations. Hint: x and y components will be needed for this problem.
Answer
To draw the free body diagram it is better to first draw a sketch of the system. In the sketch we see the string to the left ([math]\displaystyle{ \mathbf{T_1} }[/math]) of the ball makes an angle of [math]\displaystyle{ 20^\text{o} }[/math] with the ceiling, and the string to the right ([math]\displaystyle{ \mathbf{T_2} }[/math]) of the ball makes an angle [math]\displaystyle{ 45^\text{o} }[/math] with the ceiling. For the free body diagram, we first draw the force of gravity pointing straight downwards. This force should have the longest arrow due to the fact that the strings are supporting this force...therefore, it can be reasoned that this force should be greater than either of the tensions in the strings for the given angles. Next, we draw the tension forces, which point away from the ball along each respective string. [math]\displaystyle{ \mathbf{T_2} }[/math] should be longer than [math]\displaystyle{ \mathbf{T_1} }[/math] due to the fact that the tensions must balance each other along the x-axis and the y-component of [math]\displaystyle{ \mathbf{T_2} }[/math] must be greater than the y-component of [math]\displaystyle{ \mathbf{T_1} }[/math].


Now, we are ready to use Newton's First and Second Laws to create a system of force equations:
- [math]\displaystyle{ \mathbf{F_{net}} = \sum\mathbf{F} = m\mathbf{a} }[/math]
Since the ball is hanging tautly, it must NOT be moving. Therefore, the velocity and acceleration must both be [math]\displaystyle{ \mathbf{0} }[/math]:
- [math]\displaystyle{ \mathbf{F_{net}} = \sum\mathbf{F} = m\mathbf{a} = \mathbf{0} }[/math]
Next, we choose the x-axis to be horizontal, and the y-axis to be vertical, as in a typical coordinate system, since it is convenient.
Now, we begin specifically identifying the forces and their components using right triangles:
- [math]\displaystyle{ \mathbf{F_g} = \begin{bmatrix} |\mathbf{F_g}| \ \text{cos}(180^\text{o}) \\ |\mathbf{F_g}| \ \text{sin}(180^\text{o}) \end{bmatrix} = \begin{bmatrix} 0 \\ -|\mathbf{F_g}| \end{bmatrix} }[/math]
- [math]\displaystyle{ \mathbf{T_1} = \begin{bmatrix} -|\mathbf{T_1}| \ \text{cos}(20^\text{o}) \\ |\mathbf{T_1}| \ \text{sin}(20^\text{o})\end{bmatrix} }[/math]
- [math]\displaystyle{ \mathbf{T_2} = \begin{bmatrix} -|\mathbf{T_2}| \ \text{cos}(45^\text{o}) \\ |\mathbf{T_2}| \ \text{sin}(45^\text{o})\end{bmatrix} }[/math]
Next, we use Newton's Second Law to sum these forces. Since the ball is not moving, we can set this summation equal to [math]\displaystyle{ \mathbf{0} }[/math]:
- [math]\displaystyle{ \mathbf{F_{net}} = \sum\mathbf{F} = m\mathbf{a} = \mathbf{0} = \mathbf{F_g} + \mathbf{T_1} + \mathbf{T_2} }[/math]
This is equivalent to:
- [math]\displaystyle{ \begin{bmatrix} 0 \\ -|\mathbf{F_g}| \end{bmatrix} + \begin{bmatrix} -|\mathbf{T_1}| \ \text{cos}(20^\text{o}) \\ |\mathbf{T_1}| \ \text{sin}(20^\text{o})\end{bmatrix} + \begin{bmatrix} -|\mathbf{T_2}| \ \text{cos}(45^\text{o}) \\ |\mathbf{T_2}| \ \text{sin}(45^\text{o})\end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} }[/math]
Hence, we have done what the question asked and are done with this problem.
Difficult
A father pushes his son's sled horizontally with a force [math]\displaystyle{ \mathbf{F_A} }[/math] all the way down a hill on a sled of mass [math]\displaystyle{ M }[/math]. The son has a mass [math]\displaystyle{ m }[/math]. The son/sled system is accelerating down the hill. Assume the hill is shaped like an inclined plane with an angle to the horizontal ground of [math]\displaystyle{ 35^{\text{o}} }[/math] and that friction works against the sled with a coefficient of dynamic (kinetic) friction [math]\displaystyle{ \mu_k }[/math]. Draw a free-body diagram. Using your free body diagram, write a system of equations that could be used to solve for the acceleration of the son/sled system.
Answer
We start with a sketch. In this sketch, we create an inclined plane with the the specified [math]\displaystyle{ 35^{\text{o}} }[/math] angle, with the dad behind the kid pushing the sled down the hill. Some forces to be thinking about in this situation are the normal force, the applied force of the dad, the frictional force opposing the motion, and the gravitational force pulling the system straight down. To begin the free body diagram, we draw a circle to symbolize the son/sled system. Next, we draw the gravitational force as straight down, as it will always be in these Earth situations. Its length should be longer than the normal force. Otherwise, it shouldn't be compared to the other forces. Next are the frictional force and the normal force. The normal force should be normal to the inclined plane, and the frictional force should be parallel to the inclined plane, but opposite the direction of motion. Finally, the applied force of the dad should be parallel to the flat ground. The free body diagram has been created. Now, we must create a system of equations that could be solved for the acceleration of the son/sled system.


To begin, we draw an x-y plane, where the y-axis runs along the the normal force and the x-axis runs along the frictional force. This will simplify the representation of these two forces, as well as represent the gravitational force with just a couple trigonometric functions. The applied force will have the same done to it.
Newton's Second Law states the net force on a system is equal to the mass of the system times the acceleration:
- [math]\displaystyle{ \mathbf{F_{net}} = \sum \mathbf{F} = m_{system}\mathbf{a} }[/math]
We are told the son/sled system is accelerating, therefore the above equation can NOT be set equal to [math]\displaystyle{ \mathbf{0} }[/math].
We also know the son/sled system should have a combined mass of [math]\displaystyle{ M + m }[/math], where [math]\displaystyle{ M }[/math] is the mass of the sled and [math]\displaystyle{ m }[/math] is the mass of the son, as stated in the problem:
- [math]\displaystyle{ \mathbf{F_{net}} = \sum \mathbf{F} = m_{system}\mathbf{a} = (M + m) \mathbf{a} }[/math]
The angle [math]\displaystyle{ \mathbf{F_A} }[/math] makes with the chosen x-axis is [math]\displaystyle{ 35^{\text{o}} }[/math]. This can be seen from the sketch. The angle the gravitational force makes with the chosen y-axis is also [math]\displaystyle{ 35^{\text{o}} }[/math]. This can also be seen in the sketch. Therefore, the four forces considered in this system can be described as:
- [math]\displaystyle{ \mathbf{F_g} = \begin{bmatrix} |\mathbf{F_g}| \ \text{cos}(35^\text{o}) \\ |\mathbf{F_g}| \ \text{sin}(35^\text{o})\end{bmatrix} }[/math]
- [math]\displaystyle{ \mathbf{F_A} = \begin{bmatrix} |\mathbf{F_A}| \ \text{cos}(35^\text{o}) \\ |\mathbf{F_A}| \ \text{sin}(35^\text{o}) \end{bmatrix} }[/math]
- [math]\displaystyle{ \mathbf{F_f} = \begin{bmatrix} |\mathbf{F_f}| \ \text{cos}(180^\text{o}) \\ |\mathbf{F_f}| \ \text{sin}(180^\text{o}) \end{bmatrix} = \begin{bmatrix} -|\mathbf{F_f}| \\ 0 \end{bmatrix} }[/math]
- [math]\displaystyle{ \mathbf{F_N} = \begin{bmatrix} |\mathbf{F_N}| \ \text{cos}(90^\text{o}) \\ |\mathbf{F_N}| \ \text{sin}(90^\text{o}) \end{bmatrix} = \begin{bmatrix} 0 \\ |\mathbf{F_N}| \end{bmatrix} }[/math]
Using Newton's Second Law, we know that:
- [math]\displaystyle{ \mathbf{F_{net}} = \sum \mathbf{F} = m_{system}\mathbf{a} = (M + m) \mathbf{a} = \mathbf{F_g} + \mathbf{F_A} + \mathbf{F_f} + \mathbf{F_N} }[/math]
This is equivalent to:
- [math]\displaystyle{ \mathbf{a} = \frac{\begin{bmatrix} |\mathbf{F_g}| \ \text{cos}(35^\text{o}) \\ |\mathbf{F_g}| \ \text{sin}(35^\text{o})\end{bmatrix} + \begin{bmatrix} |\mathbf{F_A}| \ \text{cos}(35^\text{o}) \\ |\mathbf{F_A}| \ \text{sin}(35^\text{o}) \end{bmatrix} + \begin{bmatrix} -|\mathbf{F_A}| \\ 0 \end{bmatrix} + \begin{bmatrix} 0 \\ |\mathbf{F_N}| \end{bmatrix}}{M+m} }[/math]
Thus we have done what the problem asked.
Connectedness
Free body diagrams are the building blocks for many scientists, physicists, engineers and have many applications in the real world. They form the basis for determining a device's or building's structural stability, safety, and overall practicality.
Medical Applications

There have recently been many advances in medicine in terms of wearables and prosthetic limbs that function just like normal body parts for either congenital defects or accident recovery. Let's take a look at a leg prosthetic. While walking, a prosthetic exerts many forces on your leg such as: the force of gravity, normal force from the ground, frictional force, etc. Prosthetics move like springs, while your body moves forward it also moves up and down which causes changes in kinetic energy due to movement and changes in gravitational potential energy. While it contracts and relaxes, different energies are converted back and forth into kinetic and potential energy. In order to analyze all the forces on a prosthetic to ensure it's safety and usability, the most basic step when designing one is a free body diagram.
Buildings and Trusses
Many civil engineers and architects are responsible for building trusses, bridges, and buildings which function using the basic concepts of physics. It is important to ensure that components of a truss and bridge are in equilibrium so that one day they don't collapse. When building a truss bridge, engineers put straight members in place that form the bridge's top and bottom, and they are linked by a structure of diagonals and vertical posts. For trusses especially, all the components must remain in equilibrium, the magnitudes of forces exerted must be equal, and the components in tension and compression must be identified. In order to create a proper structure, a free body diagram must be used by engineers in the preliminary stages for design and safety purposes.
History
EDITED BY DEEPIKA RAVI, FALL 2025
Free Body Diagrams were developed alongside Newtonian physics as a graphical way to analyze what forces were acting on a system and how the system would react. More specifically, it traces its roots back to the works of Isaac Newton and later engineers who wanted to develop practical methods for applying Newton's laws. Although Newton himself did not develop the modern form of a force diagram, he developed the conceptual fondation of isolation a system and analyzing the forces acting upon it.[1] As physics and engineering developed rapidly through the Industrial Revolution, a systemic approach to statics and dynamics grew. Early engineering texts in the 1800s started to include sketches which showed loads on beams, tension in cables, and normal forces acting on supports. These sketches slowly became the standardized norm in engineering colleges. By the late 19th and early 20th centuries, free body diagrams became an essential problem solving tool, especially in the development of infrastructure, such as bridges. Take for example an analysis of the forces in a Truss Bridge.[2]
Due to their widespread usefulness, free body diagrams have not fallen out of favor with scientists and engineers. They continue to be used as a teaching and real world tool for well over a century. Free body diagrams are emphasized to be a foundational skill for students, allowing them to translate real-world systems into mathematical models. With the improvements in computer-aided models and design tools, the role of FBDs still remains essential to engineering.
References
- ↑ Dugas, René. A History of Mechanics. Routledge, 1955 Online PDF
- ↑ TeachEngineering. "Analyzing Forces in a Truss Bridge." https://www.teachengineering.org/lessons/view/ind-2472-analysis-forces-truss-bridge-lesson
See Also
Further Reading
External Links
Using Free-Body Diagrams to Solve Kinematics Problems
References
Matter and Interactions: Modern Mechanics. Volume One. 4th Edition.
http://demos.smu.ca/index.php/demos/mechanics/141-free-body-diagram
http://hyperphysics.phy-astr.gsu.edu/hbase/freeb.html
https://www.wisc-online.com/learn/natural-science/physics/tp1502/construction-of-free-body-diagrams
http://www.physicsclassroom.com/Class/newtlaws
https://sites.google.com/a/cpsdigital.org/peraplegic/human-prosthetics
http://slideplayer.com/slide/6086550/ - Tilted Axis Image
http://www.revistas.unal.edu.co/index.php/dyna/rt/printerFriendly/30749/39025 - Prosthetic Limb Image
http://www.mathalino.com/reviewer/engineering-mechanics/241-finding-resulatnt-vertical-forces-acting-fink-truss - Truss Image