First Law of Thermodynamics: Difference between revisions
No edit summary |
|||
| (107 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
[[ | ==Main Idea== | ||
The First Law of Thermodynamics is another way to state [[Conservation of Energy]] and [[The Energy Principle]]. Hence, if needed, review those topics before diving into The First Law of Thermodynamics. Heat, the transfer of thermal energy, and internal energy, the energy possessed by the constituents of the system, are forms of energy, just like [[Kinetic Energy]] and [[Potential Energy]]. We can now extend the scope of the Law of Conservation of Mechanical Energy from Work and external potential and kinetic energy to Heat and internal energy. The First Law of Thermodynamics states: although energy comes in various forms, the total quantity of energy stays the same, and the energy disappearing in one form must appear simultaneously in other forms. | |||
[[File:Firstlaw.jpg|500px|center]] | |||
The First Law of Thermodynamics states | ===Mathematical Model=== | ||
[[File:workheat.jpg|right]] | |||
The First Law of Thermodynamics states: | |||
:The change in internal energy of a system is equal to the heat added/taken away from the system plus the work done on the system/minus the work done by the system: | |||
<math> | ::<math>\Delta U_{system} = Q + W_{on system} \quad \Delta U_{system} = Q - W_{by system}</math> | ||
:<math>Q</math> and <math>W</math> are qualitatively energy in transit from the source to the receiver. | |||
:The work done on a system is equal to the negative of the work done by the system: | |||
::<math>W_{on system} = -W_{by system}</math> | |||
[[File:Thermo1.gif|right|500px]] | |||
The First Law of Thermodynamics can also be stated in a more general fashion as: | |||
:The change in total energy of the system is equal to the heat added/taken away from the system plus the work done on the system/minus the work done by the system: | |||
::<math>\Delta E_{total} = \Delta PE + \Delta KE + \Delta U \quad \Delta E_{total} = Q + W</math>, where | |||
:::<math>\Delta PE =</math> change in potential energy of the system | |||
:::<math>\Delta KE =</math> change in kinetic energy of the system | |||
:::<math>\Delta U =</math> change in internal energy of the system | |||
:Therefore: | |||
::<math>\Delta PE + \Delta KE + \Delta U = Q + W</math> | |||
:The quantity <math>\Delta PE + \Delta KE</math> is usually considered <math>0</math> by [[The Energy Principle]], leading to the previous equation of The First Law of Thermodynamics.. | |||
===Computational Model=== | |||
:'''Insert Computational Model here''' | |||
http://jersey.uoregon.edu/vlab/Thermodynamics/ | |||
This virtual experiment gives you visual representation of thermal equilibrium and how it is reached when beginning with different initial conditions. | |||
==Examples== | ==Examples== | ||
=== | ===Simple=== | ||
<math>5,000 \ J</math> of Heat is added to a closed system. Also, the internal energy of the system decreases by <math>11,000 \ J</math>. | |||
:'''a) How much Work must the system have done?''' | |||
::Referring to our [[First Law of Thermodynamics#Mathematical Model| Mathematical Model]], we know for a closed system, the change in internal energy of a the system is equal to the Heat applied to the system/lost by the system plus the Work done on the system: | |||
:::<math>\Delta U_{system} = Q + W_{on system}</math> | |||
== | ::We know the Heat added and the change in internal energy of the system. Therefore, we can find the Work done by the system by noting the Work on the system is equal to the negative of the Work done by the system: | ||
:::<math>W_{on system} = -W_{bysystem}</math> | |||
:::<math>W_{on system} = \Delta U_{system} - Q</math> | |||
:::<math>W_{bysystem} = -( \Delta U_{system} - Q)</math> | |||
:::<math>W_{bysystem} = -(-11,000 - 5,000) = 16,000 \ J</math> | |||
:The system must have done <math>16,000 \ J</math> of Work to explain the loss in internal energy but addition of Heat. | |||
===Middling=== | |||
An egg, initially at rest, is dropped onto a concrete surface and breaks. Treat the egg as the system. | |||
:'''a) What is the sign of <math>W</math>?''' | |||
::Since the egg is speeding up as it falls, Work must be being done on the egg. Thus, <math>W_{onegg}</math> is positive, and <math>W_{byegg}</math> is negative, since: | |||
:::<math>W_{onegg} = -W_{by egg}</math> | |||
:'''b) What is the sign of <math>\Delta PE</math>?''' | |||
::The change in potential energy of the egg will be negative, since it is falling towards the Earth. Let <math>h_0</math> and <math>h_f</math> be the initial and final height of the egg, respectively with <math>h_f << h_0</math>, then we have: | |||
:::<math>\Delta PE = mgh_f - mgh_0 = mg(h_f - h_0) < 0</math>, since <math>h_f << h_0</math> | |||
:'''c) What is <math>\Delta KE</math>?''' | |||
::The change in kinetic energy of the egg is <math>0</math>, due to the fact that its initial and final velocity are both <math>0</math>: | |||
:::<math>\Delta KE = \frac{1}{2}m{v_f}^2 - \frac{1}{2}m{v_0}^2 = \frac{1}{2}m({v_f}^2 - {v_0}^2) \quad \And \quad v_f = v_0 = 0 \quad \therefore \quad \Delta K = 0</math> | |||
:'''d) What is <math>\Delta U</math>?''' | |||
::No Heat is added to the system, and no chemical processes are in motion with the egg. Therefore, we can assume the internal energy of the egg is constant: | |||
:::<math>\Delta U = 0</math> | |||
:'''e) What is the sign of <math>Q</math>?''' | |||
::From our [[First Law of Thermodynamics#Mathematicla Model| Mathematical Model]], we see: | |||
:::<math>\Delta PE + \Delta KE + \Delta U = Q + W_{onegg}</math> | |||
::We also know: | |||
:::<math>\Delta PE < 0</math> | |||
:::<math>\Delta KE = 0</math> | |||
:::<math>\Delta U = 0</math> | |||
:::<math>W_{onegg} > 0</math> | |||
::So: | |||
:::<math>Q = \Delta PE - W_{onegg}</math> | |||
::We have <math>Q</math> set equal to a negative quantity minus a positive quantity. Therefore, <math>Q</math> must be a negative quantity its self: | |||
:::<math>Q < 0</math> | |||
===Difficult=== | |||
One mole of gas in a closed system undergoes a four-step Thermodynamic cycle. Using the data below, determine the numerical values for the missing quantities. | |||
{| class="wikitable" style="text-align:center; width:250px; height:250px; font-size:14pt; border:10; frame:border; rules:all; margin-left:auto; margin-right:auto" | |||
|+ Four Step Thermodynamic Cycle | |||
|- | |||
! style="border-width:3px; border-color:black; background: white" | Step | |||
! style="border-width:3px; border-color:black; background: white" | <math>\Delta U \ (J)</math> | |||
! style="border-width:3px; border-color:black; background: white" | <math>Q \ (J)</math> | |||
! style="border-width:3px; border-color:black; background: white" | <math>W_{by gas} \ (J)</math> | |||
|- | |||
| style="background: white; border-width:3px; border-color:black" | <math>1 \rightarrow 2</math> | |||
| <math>-200</math> | |||
| style="background: yellow" | '''?''' | |||
| <math>-6,000</math> | |||
|- | |||
| style="background: white; border-width:3px; border-color:black" | <math>2 \rightarrow 3</math> | |||
| style="background: yellow" | '''?''' | |||
| <math>-3,800</math> | |||
| style="background: yellow" | '''?''' | |||
|- | |||
| style="background: white; border-width:3px; border-color:black" | <math>3 \rightarrow 4</math> | |||
| style="background: yellow" | '''?''' | |||
| <math>-800</math> | |||
| <math>300</math> | |||
|- | |||
| style="background: white; border-width:3px; border-color:black" | <math>4 \rightarrow 1</math> | |||
| <math>4,700</math> | |||
| style="background: yellow" | '''?''' | |||
| style="background: yellow" | '''?''' | |||
|- | |||
| style="background: white; border-width:3px; border-color:black" | <math>1 \rightarrow2 \rightarrow 3 \rightarrow 4 \rightarrow 1</math> | |||
| style="background: yellow" | '''?''' | |||
| style="background: yellow" | '''?''' | |||
| <math>-1,400</math> | |||
|} | |||
The equation we will use for this example is: | |||
:<math>\Delta U = Q + W_{ongas}</math> | |||
:''First Analysis'': | |||
::'''Step''' <math>[1 \rightarrow 2]</math>: | |||
:::In-between steps 1 and 2, we can see from the table that the internal energy of the gas decreases by 200 Joules, and the gas does 6,000 Joules of Work on the surroundings. Thus, we can solve for the heat added/lost: | |||
::::<math>Q(12) = \Delta U(12) - W_{on gas}(12) = \Delta U(12) + W_{bygas}(12) = -200 - 6,000 = -6,200 \ J</math> | |||
::'''Step''' <math>[2 \rightarrow 3]</math>: | |||
::In-between steps 2 and 3, we can see from the table that the heat lost by the gas is 3,800 Joules. This is not enough information to solve for anything, so we'll move onto the next step. | |||
::'''Step''' <math>[3 \rightarrow 4]</math>: | |||
:::In-between steps 3 and 4, we can see from the table that the heat lost by the system is 800 Joules, and the Work done by the gas is 300 Joules. Thus, we can solve for the change in internal energy: | |||
::::<math>\Delta U(34) = Q(34) + W_{ongas}(34) = Q(34) - W_{bygas}(34)</math> | |||
::::<math>\Delta U = -800 - 300 = -1,100 \ J</math> | |||
::'''Step''' <math>[4 \rightarrow 1]</math>: | |||
:::In-between steps 4 and 1, we see that the internal energy of the gas increases by 4,700 Joules. This is not enough information to solve for the components, so we'll move onto the next step. | |||
::'''Step''' <math>[1 \rightarrow 2 \rightarrow 3 \rightarrow 4 \rightarrow 1]</math>: | |||
:::This step signifies the whole cycle. In a cycle of a closed system, energy will be conserved, a fact we have been utilizing. This also means the change in internal energy will be a 0 Joules once we have completed the cycle. We can use this information: | |||
::::<math>\Delta U(12341) = Q(12341) + W_{ongas}(12341) = Q(12341) - W_{bygas}(12341) = 0</math> | |||
::::<math>Q(12341) = W_{bygas}(12341) = -1,400 \ J</math> | |||
:::The change in internal energy is also equal to the sum of the changes of internal energy in each step. We can use this to solve for the change in internal between steps 2 and 3: | |||
::::<math>\Delta U_{total} = \Delta U_{12} + \Delta U_{23} + \Delta U_{34} + \Delta U_{41} = 0</math> | |||
::::<math>\Delta U_{23} = - \Delta U_{12} - \Delta U_{34} - \Delta U_{41} = -(-200) - (-1,100) - (4,700) = 200 + 1,100 - 4,700 = - 3,400 \ J</math> | |||
:''Second Analysis'': | |||
{| class="wikitable" style="text-align:center; width:250px; height:250px; font-size:14pt; border:10; frame:border; rules:all; margin-left:auto; margin-right:auto" | |||
|+ Four Step Thermodynamic Cycle | |||
|- | |||
! style="border-width:3px; border-color:black; background: white" | Step | |||
! style="border-width:3px; border-color:black; background: white" | <math>\Delta U \ (J)</math> | |||
! style="border-width:3px; border-color:black; background: white" | <math>Q \ (J)</math> | |||
! style="border-width:3px; border-color:black; background: white" | <math>W_{by gas} \ (J)</math> | |||
|- | |||
| style="background: white; border-width:3px; border-color:black" | <math>1 \rightarrow 2</math> | |||
| <math>-200</math> | |||
| <math>-6,200</math> | |||
| <math>-6,000</math> | |||
|- | |||
| style="background: white; border-width:3px; border-color:black" | <math>2 \rightarrow 3</math> | |||
| <math>-3,400</math> | |||
| <math>-3,800</math> | |||
| style="background: yellow" | '''?''' | |||
|- | |||
| style="background: white; border-width:3px; border-color:black" | <math>3 \rightarrow 4</math> | |||
| <math>-1,100</math> | |||
| <math>-800</math> | |||
| <math>300</math> | |||
|- | |||
| style="background: white; border-width:3px; border-color:black" | <math>4 \rightarrow 1</math> | |||
| <math>4,700</math> | |||
| style="background: yellow" | '''?''' | |||
| style="background: yellow" | '''?''' | |||
|- | |||
| style="background: white; border-width:3px; border-color:black" | <math>1 \rightarrow2 \rightarrow 3 \rightarrow 4 \rightarrow 1</math> | |||
| <math>0</math> | |||
| <math>-1,400</math> | |||
| <math>-1,400</math> | |||
|} | |||
::Step [<math>2 \rightarrow 3</math>]: | |||
:::We now have enough information to solve for the Work done by the gas in the step in-between 2 and 3: | |||
::::<math>\Delta U(23) = Q(23) + W_{on gas}(23) = Q(23) - W_{by gas}(23)</math> | |||
::::<math>W_{by gas}(23) = Q(23) - \Delta U(23) = -3,800 + 3,400 = -400 \ J</math> | |||
::Step [<math>4 \rightarrow 1</math>]: | |||
:::For the table to be self-consistent, the total in each column (bottom row) must equal the sum of the the other rows within that column. Thus: | |||
::::<math>Q_{12341} = Q_{12} + Q_{23} + Q_{34} + Q_{41} \quad \And \quad W_{12341} = W_{12} + W_{23} + W_{34} + W_{41}</math> | |||
::::<math>Q_{41} = Q_{12341} - (Q_{12} + Q_{23} + Q_{34}) \quad \And \quad W_{41} = W_{12341} - (W_{12} + W_{23} + W_{34})</math> | |||
::::<math>Q_{41} = -1,400 - (-6,200 - 3,800 - 800) = -1,400 + 10,800 = 9,400 \ J</math> | |||
::::<math>W_{41} = -1,400 - (-6,000 - 400 + 300) = -1,400 + 6,100 = 4,700 \ J</math> | |||
We have filled in the table: | |||
{| class="wikitable" style="text-align:center; width:250px; height:250px; font-size:14pt; border:10; frame:border; rules:all; margin-left:auto; margin-right:auto" | |||
|+ Four Step Thermodynamic Cycle | |||
|- | |||
! style="border-width:3px; border-color:black; background: white" | Step | |||
! style="border-width:3px; border-color:black; background: white" | <math>\Delta U \ (J)</math> | |||
! style="border-width:3px; border-color:black; background: white" | <math>Q \ (J)</math> | |||
! style="border-width:3px; border-color:black; background: white" | <math>W_{by gas} \ (J)</math> | |||
|- | |||
| style="background: white; border-width:3px; border-color:black" | <math>1 \rightarrow 2</math> | |||
| <math>-200</math> | |||
| <math>-6,200</math> | |||
| <math>-6,000</math> | |||
|- | |||
| style="background: white; border-width:3px; border-color:black" | <math>2 \rightarrow 3</math> | |||
| <math>-3,400</math> | |||
| <math>-3,800</math> | |||
| <math>-400</math> | |||
|- | |||
| style="background: white; border-width:3px; border-color:black" | <math>3 \rightarrow 4</math> | |||
| <math>-1,100</math> | |||
| <math>-800</math> | |||
| <math>300</math> | |||
|- | |||
| style="background: white; border-width:3px; border-color:black" | <math>4 \rightarrow 1</math> | |||
| <math>4,700</math> | |||
| <math>9,400</math> | |||
| <math>4,700</math> | |||
|- | |||
| style="background: white; border-width:3px; border-color:black" | <math>1 \rightarrow2 \rightarrow 3 \rightarrow 4 \rightarrow 1</math> | |||
| <math>0</math> | |||
| <math>-1,400</math> | |||
| <math>-1,400</math> | |||
|} | |||
==Connectedness== | |||
1. How is this topic connected to something that you are interested in? | |||
*In physics, I've always encountered the subject of "Thermodynamics" with excitement. I always loved to deal with Temperatures and <math>mC \Delta T</math> is the equation that I enjoy utilizing the most. Being able to explain the mechanism of our fingers instantly turning cold as they touch the ice or in reverse, our hands warming up by simply holding a cup of hot cocoa as the flow of heat from a hotter object to colder object is inspring. Plus, there are even specific quantitative relationships that exist between the Heat, Work, and internal energy, and we are able to apply them exactly into our daily lives, thus the science of "Thermodynamics" is indeed extremely empowering! | |||
2. How is it connected to your major? | |||
* I major in Chemical Engineering. There are two-semesters worth of curriculum dedicated solely to "Thermodynamics" in Chemical Engineering. The fundamental laws of Thermodynamics embody mathematical deduction to a network of equations which can be applied in all branches of science and engineering. Chemical Engineers provide solutions to a wide range of problems and, many of them have to do with calculating the Heat and Work for various physical and chemical processes. Thus, "Thermodynamics" is one of the skeletal parts of Chemical Engineering. | |||
3. Is there an interesting industrial application? | |||
* Thermodynamics is relevant in the energy, transportation, petrochemical, and HVAC industries. | |||
== | ==History== | ||
[[File:GW635H289.jpg|right]] | |||
James P. Joule's experiments with Heat and Work made major contributions to the formation of the modern concept of Heat. Joule put certain amounts of mercury, water, and oil into an insulated container and mixed the liquid using a rotating stirrer. He carefully measured how much work was done by the stirrer to the liquid and the change in temperature that the liquid experienced. Joule discovered that for a particular fluid, a fixed amount of Work is required per unit mass in order to raise its Temperature by one degree. Joule established that Heat is a form of energy and that there is a quantitative relationship between Heat and Work. | |||
[[File:Thermo.jpg|150px|right]] | |||
[[File:Steam.jpeg|left|250px]] | |||
The science of Thermodynamics originated in the 19th century in order to explain the mechanism of steam engines. The term 'Thermodynamics' means power developed from Heat, and Thermodynamics deals with the relationship between Heat and other forms of energy. One can apply Thermodynamics to a problem, beginning with identifying a body of matter called the system. A system's Thermodynamic state is defined by several macroscopic properties that depend on the fundamental dimensions such as time, temperature, mass, length, etc. | |||
==See also== | |||
===Further reading=== | ===Further reading=== | ||
* Thermodynamics (Dover Book on Physics) by Enrico Fermi | |||
* Engineering Thermodynamics by P. K. Nag | |||
* M. J. Moran and H. N. Shapiro, ‘Fundamentals of Engineering Thermodynamics’, Fourth Edition, Wiley, New York, 2000 | |||
* Thermodynamics: An Engineering Approach by Cengel, Ya and Boles, M.A. | |||
* Introduction to Chemical Engineering Thermodynamics, Seventh Edition, by J.M. Smith, H.C. Van Ness, M.M. Abbott | |||
===External links=== | ===External links=== | ||
| Line 46: | Line 322: | ||
* http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/firlaw.html | * http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/firlaw.html | ||
* [http://www.wiley.com/college/moran/CL_0471465704_S/thermonet/docs/user/index.html ThermoNet] | * [http://www.wiley.com/college/moran/CL_0471465704_S/thermonet/docs/user/index.html ThermoNet] | ||
* [https://www.khanacademy.org/science/physics/thermodynamics/laws-of-thermodynamics/v/first-law-of-thermodynamics-internal-energy Khan Academy: First Law of Thermodynamics] | |||
* http://www.ncert.nic.in/html/learning_basket/energy10class/joule's%20experiment.htm | |||
* http://demonstrations.wolfram.com/JoulesExperiment/ | |||
* https://www.wolframscience.com/reference/notes/1019b | |||
* http://www.livescience.com/50776-thermodynamics.html | |||
* [https://www.youtube.com/watch?v=5yOhSIAIPRE Mechanical Equivalent of Heat] | |||
* https://en.wikipedia.org/wiki/First_law_of_thermodynamics | |||
* https://courses.lumenlearning.com/introchem/chapter/the-three-laws-of-thermodynamics/ | |||
* https://www.khanacademy.org/science/physics/thermodynamics/laws-of-thermodynamics/a/what-is-the-first-law-of-thermodynamics | |||
* http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/firlaw.html | |||
* https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules_(Physical_and_Theoretical_Chemistry)/Thermodynamics/The_Four_Laws_of_Thermodynamics/First_Law_of_Thermodynamics | |||
==References== | ==References== | ||
* Callen, Herbert B. (1985). Thermodynamics and an Introduction to Thermostatistics. Wiley. p. 5,37. | * Callen, Herbert B. (1985). Thermodynamics and an Introduction to Thermostatistics. Wiley. p. 5,37. | ||
* http://fineartamerica.com/featured/1-thermodynamics-conceptual-artwork-richard-bizley.html | * http://fineartamerica.com/featured/1-thermodynamics-conceptual-artwork-richard-bizley.html | ||
* http://www.humanthermodynamics.com/Clausius.html | |||
* http://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/node15.html | |||
* http://www.juliantrubin.com/bigten/mechanical_equivalent_of_heat.html | |||
* https://www.grc.nasa.gov/www/k-12/airplane/thermo1.html | |||
* https://www2.estrellamountain.edu/faculty/farabee/biobk/BioBookEner1.html | |||
* http://www2.phy.ilstu.edu/~hmb/phy325/TPCh.7.1(09).pdf | |||
* http://www.shashaiseminar.com/notes/a-level/zimsec/physics/heat-2/ | |||
* https://www.asee.org/public/conferences/8/papers/4611/download | |||
Latest revision as of 09:42, 4 August 2019
Main Idea
The First Law of Thermodynamics is another way to state Conservation of Energy and The Energy Principle. Hence, if needed, review those topics before diving into The First Law of Thermodynamics. Heat, the transfer of thermal energy, and internal energy, the energy possessed by the constituents of the system, are forms of energy, just like Kinetic Energy and Potential Energy. We can now extend the scope of the Law of Conservation of Mechanical Energy from Work and external potential and kinetic energy to Heat and internal energy. The First Law of Thermodynamics states: although energy comes in various forms, the total quantity of energy stays the same, and the energy disappearing in one form must appear simultaneously in other forms.
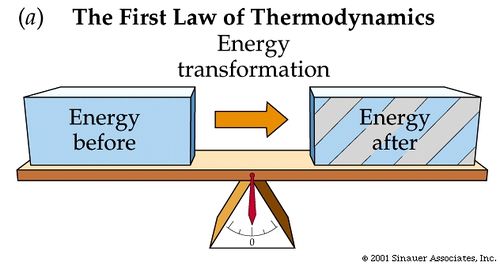
Mathematical Model
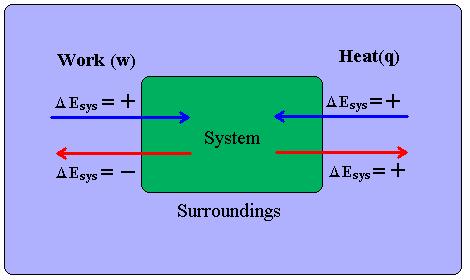
The First Law of Thermodynamics states:
- The change in internal energy of a system is equal to the heat added/taken away from the system plus the work done on the system/minus the work done by the system:
- [math]\displaystyle{ \Delta U_{system} = Q + W_{on system} \quad \Delta U_{system} = Q - W_{by system} }[/math]
- [math]\displaystyle{ Q }[/math] and [math]\displaystyle{ W }[/math] are qualitatively energy in transit from the source to the receiver.
- The work done on a system is equal to the negative of the work done by the system:
- [math]\displaystyle{ W_{on system} = -W_{by system} }[/math]
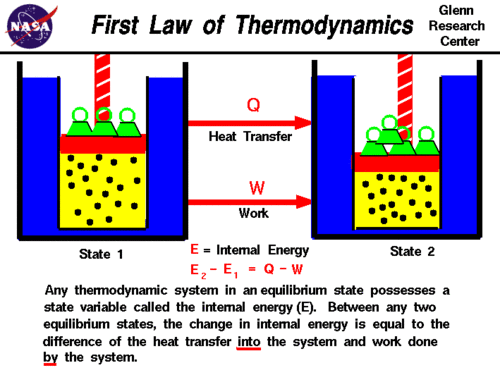
The First Law of Thermodynamics can also be stated in a more general fashion as:
- The change in total energy of the system is equal to the heat added/taken away from the system plus the work done on the system/minus the work done by the system:
- [math]\displaystyle{ \Delta E_{total} = \Delta PE + \Delta KE + \Delta U \quad \Delta E_{total} = Q + W }[/math], where
- [math]\displaystyle{ \Delta PE = }[/math] change in potential energy of the system
- [math]\displaystyle{ \Delta KE = }[/math] change in kinetic energy of the system
- [math]\displaystyle{ \Delta U = }[/math] change in internal energy of the system
- Therefore:
- [math]\displaystyle{ \Delta PE + \Delta KE + \Delta U = Q + W }[/math]
- The quantity [math]\displaystyle{ \Delta PE + \Delta KE }[/math] is usually considered [math]\displaystyle{ 0 }[/math] by The Energy Principle, leading to the previous equation of The First Law of Thermodynamics..
Computational Model
- Insert Computational Model here
http://jersey.uoregon.edu/vlab/Thermodynamics/
This virtual experiment gives you visual representation of thermal equilibrium and how it is reached when beginning with different initial conditions.
Examples
Simple
[math]\displaystyle{ 5,000 \ J }[/math] of Heat is added to a closed system. Also, the internal energy of the system decreases by [math]\displaystyle{ 11,000 \ J }[/math].
- a) How much Work must the system have done?
- Referring to our Mathematical Model, we know for a closed system, the change in internal energy of a the system is equal to the Heat applied to the system/lost by the system plus the Work done on the system:
- [math]\displaystyle{ \Delta U_{system} = Q + W_{on system} }[/math]
- We know the Heat added and the change in internal energy of the system. Therefore, we can find the Work done by the system by noting the Work on the system is equal to the negative of the Work done by the system:
- [math]\displaystyle{ W_{on system} = -W_{bysystem} }[/math]
- [math]\displaystyle{ W_{on system} = \Delta U_{system} - Q }[/math]
- [math]\displaystyle{ W_{bysystem} = -( \Delta U_{system} - Q) }[/math]
- [math]\displaystyle{ W_{bysystem} = -(-11,000 - 5,000) = 16,000 \ J }[/math]
- The system must have done [math]\displaystyle{ 16,000 \ J }[/math] of Work to explain the loss in internal energy but addition of Heat.
Middling
An egg, initially at rest, is dropped onto a concrete surface and breaks. Treat the egg as the system.
- a) What is the sign of [math]\displaystyle{ W }[/math]?
- Since the egg is speeding up as it falls, Work must be being done on the egg. Thus, [math]\displaystyle{ W_{onegg} }[/math] is positive, and [math]\displaystyle{ W_{byegg} }[/math] is negative, since:
- [math]\displaystyle{ W_{onegg} = -W_{by egg} }[/math]
- b) What is the sign of [math]\displaystyle{ \Delta PE }[/math]?
- The change in potential energy of the egg will be negative, since it is falling towards the Earth. Let [math]\displaystyle{ h_0 }[/math] and [math]\displaystyle{ h_f }[/math] be the initial and final height of the egg, respectively with [math]\displaystyle{ h_f \lt \lt h_0 }[/math], then we have:
- [math]\displaystyle{ \Delta PE = mgh_f - mgh_0 = mg(h_f - h_0) \lt 0 }[/math], since [math]\displaystyle{ h_f \lt \lt h_0 }[/math]
- c) What is [math]\displaystyle{ \Delta KE }[/math]?
- The change in kinetic energy of the egg is [math]\displaystyle{ 0 }[/math], due to the fact that its initial and final velocity are both [math]\displaystyle{ 0 }[/math]:
- [math]\displaystyle{ \Delta KE = \frac{1}{2}m{v_f}^2 - \frac{1}{2}m{v_0}^2 = \frac{1}{2}m({v_f}^2 - {v_0}^2) \quad \And \quad v_f = v_0 = 0 \quad \therefore \quad \Delta K = 0 }[/math]
- d) What is [math]\displaystyle{ \Delta U }[/math]?
- No Heat is added to the system, and no chemical processes are in motion with the egg. Therefore, we can assume the internal energy of the egg is constant:
- [math]\displaystyle{ \Delta U = 0 }[/math]
- e) What is the sign of [math]\displaystyle{ Q }[/math]?
- From our Mathematical Model, we see:
- [math]\displaystyle{ \Delta PE + \Delta KE + \Delta U = Q + W_{onegg} }[/math]
- We also know:
- [math]\displaystyle{ \Delta PE \lt 0 }[/math]
- [math]\displaystyle{ \Delta KE = 0 }[/math]
- [math]\displaystyle{ \Delta U = 0 }[/math]
- [math]\displaystyle{ W_{onegg} \gt 0 }[/math]
- So:
- [math]\displaystyle{ Q = \Delta PE - W_{onegg} }[/math]
- We have [math]\displaystyle{ Q }[/math] set equal to a negative quantity minus a positive quantity. Therefore, [math]\displaystyle{ Q }[/math] must be a negative quantity its self:
- [math]\displaystyle{ Q \lt 0 }[/math]
Difficult
One mole of gas in a closed system undergoes a four-step Thermodynamic cycle. Using the data below, determine the numerical values for the missing quantities.
| Step | [math]\displaystyle{ \Delta U \ (J) }[/math] | [math]\displaystyle{ Q \ (J) }[/math] | [math]\displaystyle{ W_{by gas} \ (J) }[/math] |
|---|---|---|---|
| [math]\displaystyle{ 1 \rightarrow 2 }[/math] | [math]\displaystyle{ -200 }[/math] | ? | [math]\displaystyle{ -6,000 }[/math] |
| [math]\displaystyle{ 2 \rightarrow 3 }[/math] | ? | [math]\displaystyle{ -3,800 }[/math] | ? |
| [math]\displaystyle{ 3 \rightarrow 4 }[/math] | ? | [math]\displaystyle{ -800 }[/math] | [math]\displaystyle{ 300 }[/math] |
| [math]\displaystyle{ 4 \rightarrow 1 }[/math] | [math]\displaystyle{ 4,700 }[/math] | ? | ? |
| [math]\displaystyle{ 1 \rightarrow2 \rightarrow 3 \rightarrow 4 \rightarrow 1 }[/math] | ? | ? | [math]\displaystyle{ -1,400 }[/math] |
The equation we will use for this example is:
- [math]\displaystyle{ \Delta U = Q + W_{ongas} }[/math]
- First Analysis:
- Step [math]\displaystyle{ [1 \rightarrow 2] }[/math]:
- In-between steps 1 and 2, we can see from the table that the internal energy of the gas decreases by 200 Joules, and the gas does 6,000 Joules of Work on the surroundings. Thus, we can solve for the heat added/lost:
- [math]\displaystyle{ Q(12) = \Delta U(12) - W_{on gas}(12) = \Delta U(12) + W_{bygas}(12) = -200 - 6,000 = -6,200 \ J }[/math]
- Step [math]\displaystyle{ [2 \rightarrow 3] }[/math]:
- In-between steps 2 and 3, we can see from the table that the heat lost by the gas is 3,800 Joules. This is not enough information to solve for anything, so we'll move onto the next step.
- Step [math]\displaystyle{ [3 \rightarrow 4] }[/math]:
- In-between steps 3 and 4, we can see from the table that the heat lost by the system is 800 Joules, and the Work done by the gas is 300 Joules. Thus, we can solve for the change in internal energy:
- [math]\displaystyle{ \Delta U(34) = Q(34) + W_{ongas}(34) = Q(34) - W_{bygas}(34) }[/math]
- [math]\displaystyle{ \Delta U = -800 - 300 = -1,100 \ J }[/math]
- Step [math]\displaystyle{ [4 \rightarrow 1] }[/math]:
- In-between steps 4 and 1, we see that the internal energy of the gas increases by 4,700 Joules. This is not enough information to solve for the components, so we'll move onto the next step.
- Step [math]\displaystyle{ [1 \rightarrow 2 \rightarrow 3 \rightarrow 4 \rightarrow 1] }[/math]:
- This step signifies the whole cycle. In a cycle of a closed system, energy will be conserved, a fact we have been utilizing. This also means the change in internal energy will be a 0 Joules once we have completed the cycle. We can use this information:
- [math]\displaystyle{ \Delta U(12341) = Q(12341) + W_{ongas}(12341) = Q(12341) - W_{bygas}(12341) = 0 }[/math]
- [math]\displaystyle{ Q(12341) = W_{bygas}(12341) = -1,400 \ J }[/math]
- The change in internal energy is also equal to the sum of the changes of internal energy in each step. We can use this to solve for the change in internal between steps 2 and 3:
- [math]\displaystyle{ \Delta U_{total} = \Delta U_{12} + \Delta U_{23} + \Delta U_{34} + \Delta U_{41} = 0 }[/math]
- [math]\displaystyle{ \Delta U_{23} = - \Delta U_{12} - \Delta U_{34} - \Delta U_{41} = -(-200) - (-1,100) - (4,700) = 200 + 1,100 - 4,700 = - 3,400 \ J }[/math]
- Second Analysis:
| Step | [math]\displaystyle{ \Delta U \ (J) }[/math] | [math]\displaystyle{ Q \ (J) }[/math] | [math]\displaystyle{ W_{by gas} \ (J) }[/math] |
|---|---|---|---|
| [math]\displaystyle{ 1 \rightarrow 2 }[/math] | [math]\displaystyle{ -200 }[/math] | [math]\displaystyle{ -6,200 }[/math] | [math]\displaystyle{ -6,000 }[/math] |
| [math]\displaystyle{ 2 \rightarrow 3 }[/math] | [math]\displaystyle{ -3,400 }[/math] | [math]\displaystyle{ -3,800 }[/math] | ? |
| [math]\displaystyle{ 3 \rightarrow 4 }[/math] | [math]\displaystyle{ -1,100 }[/math] | [math]\displaystyle{ -800 }[/math] | [math]\displaystyle{ 300 }[/math] |
| [math]\displaystyle{ 4 \rightarrow 1 }[/math] | [math]\displaystyle{ 4,700 }[/math] | ? | ? |
| [math]\displaystyle{ 1 \rightarrow2 \rightarrow 3 \rightarrow 4 \rightarrow 1 }[/math] | [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ -1,400 }[/math] | [math]\displaystyle{ -1,400 }[/math] |
- Step [[math]\displaystyle{ 2 \rightarrow 3 }[/math]]:
- We now have enough information to solve for the Work done by the gas in the step in-between 2 and 3:
- [math]\displaystyle{ \Delta U(23) = Q(23) + W_{on gas}(23) = Q(23) - W_{by gas}(23) }[/math]
- [math]\displaystyle{ W_{by gas}(23) = Q(23) - \Delta U(23) = -3,800 + 3,400 = -400 \ J }[/math]
- Step [[math]\displaystyle{ 4 \rightarrow 1 }[/math]]:
- For the table to be self-consistent, the total in each column (bottom row) must equal the sum of the the other rows within that column. Thus:
- [math]\displaystyle{ Q_{12341} = Q_{12} + Q_{23} + Q_{34} + Q_{41} \quad \And \quad W_{12341} = W_{12} + W_{23} + W_{34} + W_{41} }[/math]
- [math]\displaystyle{ Q_{41} = Q_{12341} - (Q_{12} + Q_{23} + Q_{34}) \quad \And \quad W_{41} = W_{12341} - (W_{12} + W_{23} + W_{34}) }[/math]
- [math]\displaystyle{ Q_{41} = -1,400 - (-6,200 - 3,800 - 800) = -1,400 + 10,800 = 9,400 \ J }[/math]
- [math]\displaystyle{ W_{41} = -1,400 - (-6,000 - 400 + 300) = -1,400 + 6,100 = 4,700 \ J }[/math]
We have filled in the table:
| Step | [math]\displaystyle{ \Delta U \ (J) }[/math] | [math]\displaystyle{ Q \ (J) }[/math] | [math]\displaystyle{ W_{by gas} \ (J) }[/math] |
|---|---|---|---|
| [math]\displaystyle{ 1 \rightarrow 2 }[/math] | [math]\displaystyle{ -200 }[/math] | [math]\displaystyle{ -6,200 }[/math] | [math]\displaystyle{ -6,000 }[/math] |
| [math]\displaystyle{ 2 \rightarrow 3 }[/math] | [math]\displaystyle{ -3,400 }[/math] | [math]\displaystyle{ -3,800 }[/math] | [math]\displaystyle{ -400 }[/math] |
| [math]\displaystyle{ 3 \rightarrow 4 }[/math] | [math]\displaystyle{ -1,100 }[/math] | [math]\displaystyle{ -800 }[/math] | [math]\displaystyle{ 300 }[/math] |
| [math]\displaystyle{ 4 \rightarrow 1 }[/math] | [math]\displaystyle{ 4,700 }[/math] | [math]\displaystyle{ 9,400 }[/math] | [math]\displaystyle{ 4,700 }[/math] |
| [math]\displaystyle{ 1 \rightarrow2 \rightarrow 3 \rightarrow 4 \rightarrow 1 }[/math] | [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ -1,400 }[/math] | [math]\displaystyle{ -1,400 }[/math] |
Connectedness
1. How is this topic connected to something that you are interested in?
- In physics, I've always encountered the subject of "Thermodynamics" with excitement. I always loved to deal with Temperatures and [math]\displaystyle{ mC \Delta T }[/math] is the equation that I enjoy utilizing the most. Being able to explain the mechanism of our fingers instantly turning cold as they touch the ice or in reverse, our hands warming up by simply holding a cup of hot cocoa as the flow of heat from a hotter object to colder object is inspring. Plus, there are even specific quantitative relationships that exist between the Heat, Work, and internal energy, and we are able to apply them exactly into our daily lives, thus the science of "Thermodynamics" is indeed extremely empowering!
2. How is it connected to your major?
- I major in Chemical Engineering. There are two-semesters worth of curriculum dedicated solely to "Thermodynamics" in Chemical Engineering. The fundamental laws of Thermodynamics embody mathematical deduction to a network of equations which can be applied in all branches of science and engineering. Chemical Engineers provide solutions to a wide range of problems and, many of them have to do with calculating the Heat and Work for various physical and chemical processes. Thus, "Thermodynamics" is one of the skeletal parts of Chemical Engineering.
3. Is there an interesting industrial application?
- Thermodynamics is relevant in the energy, transportation, petrochemical, and HVAC industries.
History
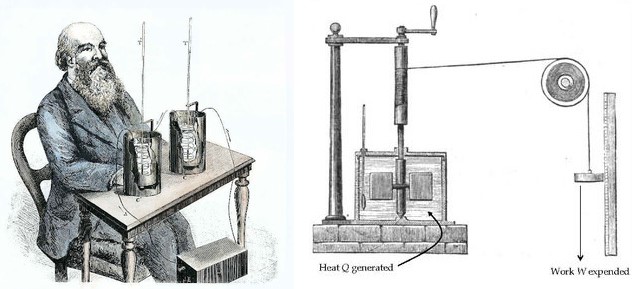
James P. Joule's experiments with Heat and Work made major contributions to the formation of the modern concept of Heat. Joule put certain amounts of mercury, water, and oil into an insulated container and mixed the liquid using a rotating stirrer. He carefully measured how much work was done by the stirrer to the liquid and the change in temperature that the liquid experienced. Joule discovered that for a particular fluid, a fixed amount of Work is required per unit mass in order to raise its Temperature by one degree. Joule established that Heat is a form of energy and that there is a quantitative relationship between Heat and Work.


The science of Thermodynamics originated in the 19th century in order to explain the mechanism of steam engines. The term 'Thermodynamics' means power developed from Heat, and Thermodynamics deals with the relationship between Heat and other forms of energy. One can apply Thermodynamics to a problem, beginning with identifying a body of matter called the system. A system's Thermodynamic state is defined by several macroscopic properties that depend on the fundamental dimensions such as time, temperature, mass, length, etc.
See also
Further reading
- Thermodynamics (Dover Book on Physics) by Enrico Fermi
- Engineering Thermodynamics by P. K. Nag
- M. J. Moran and H. N. Shapiro, ‘Fundamentals of Engineering Thermodynamics’, Fourth Edition, Wiley, New York, 2000
- Thermodynamics: An Engineering Approach by Cengel, Ya and Boles, M.A.
- Introduction to Chemical Engineering Thermodynamics, Seventh Edition, by J.M. Smith, H.C. Van Ness, M.M. Abbott
External links
- http://www.scientificamerican.com/article/bring-science-home-reaction-time/
- http://www.physlink.com/Education/AskExperts/ae280.cfm
- http://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/node15.html
- http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/firlaw.html
- ThermoNet
- Khan Academy: First Law of Thermodynamics
- http://www.ncert.nic.in/html/learning_basket/energy10class/joule's%20experiment.htm
- http://demonstrations.wolfram.com/JoulesExperiment/
- https://www.wolframscience.com/reference/notes/1019b
- http://www.livescience.com/50776-thermodynamics.html
- Mechanical Equivalent of Heat
- https://en.wikipedia.org/wiki/First_law_of_thermodynamics
- https://courses.lumenlearning.com/introchem/chapter/the-three-laws-of-thermodynamics/
- https://www.khanacademy.org/science/physics/thermodynamics/laws-of-thermodynamics/a/what-is-the-first-law-of-thermodynamics
- http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/firlaw.html
- https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules_(Physical_and_Theoretical_Chemistry)/Thermodynamics/The_Four_Laws_of_Thermodynamics/First_Law_of_Thermodynamics
References
- Callen, Herbert B. (1985). Thermodynamics and an Introduction to Thermostatistics. Wiley. p. 5,37.
- http://fineartamerica.com/featured/1-thermodynamics-conceptual-artwork-richard-bizley.html
- http://www.humanthermodynamics.com/Clausius.html
- http://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/node15.html
- http://www.juliantrubin.com/bigten/mechanical_equivalent_of_heat.html
- https://www.grc.nasa.gov/www/k-12/airplane/thermo1.html
- https://www2.estrellamountain.edu/faculty/farabee/biobk/BioBookEner1.html
- http://www2.phy.ilstu.edu/~hmb/phy325/TPCh.7.1(09).pdf
- http://www.shashaiseminar.com/notes/a-level/zimsec/physics/heat-2/
- https://www.asee.org/public/conferences/8/papers/4611/download