Insulators: Difference between revisions
Zbartolek3 (talk | contribs) |
Tag: Undo |
||
| (71 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
'''Ammar Ladhani Spring 2022''' | |||
[[File:Pylon.detail.arp.750pix.jpg|thumb|350 px|A ceramic insulator used on a powerline. Ceramic has a very high resistivity, making it an excellent insulator.]] | |||
[[File:Insulator railways.jpg|thumb|350 px|Another example of an insulator]] | |||
Insulators are characterized by the limited ability of charge to flow through them. In a typical insulator, electrons are bound to individual atoms or molecules, preventing easy flow through the material. [[Conductors]], in contrast, are characterized by the presence of free charges (typically electrons), which can move easily and thus allow charge to flow easily through the material. Metals are the prototypical conductor, with large numbers of electrons in weakly bound valence orbitals. Saltwater also acts as a conductor, since the ions dissolved in the water respond easily to electrical fields, and so transmit current. Typical insulators include structures of organic molecules, which are composed primarily of covalent bonds, and therefore inhibit the easy flow of electrons. | |||
, | |||
==The Main Idea== | |||
An insulator is a material that restricts the flow of charges due to an applied electric field. When a charge, such as an electron, is put under an applied field, it will experience a force that causes it to move. In an insulator, however, all electrons are tightly bound to the molecule they belong to; rather than the free-flowing "sea of electrons" in metals. Since there are no free, mobile electrons in an insulator, no charges will move through the material. An applied electric field still causes a force on the electrons in the insulator though, which results in the polarization of the insulator. When an insulator polarizes, the electron orbital will shift, as described in [[Polarization]], resulting in induced dipoles. While the effect of each induced dipole is minuscule, the additive-induced polarization of the whole material can have a large effect. | |||
The classification of a material as an insulator or conductor is determined by its [[Conductivity and Resistivity|conductivity and resistivity]]. As described on that page, these are two sides of the same coin, with each being the reciprocal of the other. Perfect insulators are a non-physical idealization, as in any material a small number of charges will still be able to move, especially when a very high voltage is applied. Insulators are ubiquitous in everyday life since if one is working with electricity, one wishes to restrain where it will go. Although the typical insulator we will consider is characterized by the presence of covalent bonds, many other insulating materials exist: air, for example, is an insulator, since it is very difficult for the current to flow through it unaided. In the presence of sufficiently high voltages, this results in lightning (or, on a smaller scale, sparking), in which the air is ionized, producing a viable conducting channel for the current to flow. | |||
'''Band Theory''' | |||
Electrons tend to seek the lowest energy state in their configuration, and the highest characteristic state, or band, at which the electrons of an element have filled up is called the Fermi level. Only electrons near the Fermi level are allowed to "jump" to another atom, which is how the electron sea of metals works. Metals have many electrons near their Fermi levels, allowing them to have great conductivity as compared to other materials. The opposite is true for insulators. The amount of electrons in an insulator available for conduction is close to none, meaning a high voltage potential at one end of the insulator will cause little to no change in the electrical structure of the insulator. | |||
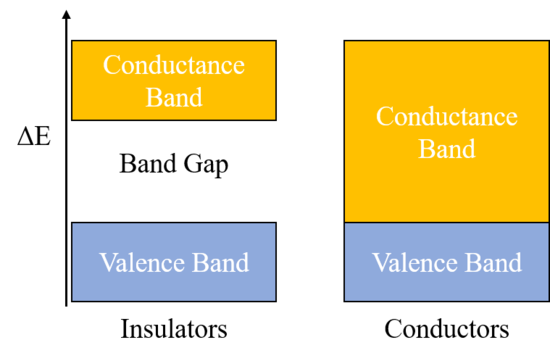
The band theory is used to describe the energy levels of valence electrons of atoms. As you may have seen with UV-spectroscopy, electrons for a single atom exist in distinct energy levels; the energy is quantized, meaning the electrons can only exist at specific energy amounts and not in between two steps. For material, the band theory takes into account multiple atoms, which results in a wider energy band/range rather than discrete steps. These bands are the valence band, where all of the valences electrons exist at the ground state, and the conductance band; the gap between these is known as the bandgap. Because the valence shells of atoms in an insulator are full due to either covalent or ionic bonding, the valence state is very stable, and a large amount of energy must be put in to get electrons to jump from the valence band to the conductance band; this means that the bandgap for an insulator is very large. A larger bandgap means a worse conductor. For conductors, the bandgap is zero and electrons can jump straight from the valence band to the conductance band with only a small amount of energy put in. The diagram below demonstrates the band diagram for insulators versus conductors. | |||
[[File:BandTheory.png|550 px]] | |||
'''Polarization of Insulators''' | |||
In insulators, all charged particles are tightly bound to the molecules making up the material. When an electric field is applied, the charged particles (electrons) in an insulator shift position slightly but still stay bound to the molecules. The largest distance the charged particles can move is about one atomic diameter, which is <math>1^{-10}</math> m. Because the mobile charge is displaced by such a small distance, the polarization happens very quickly. The whole process can generally take less than a nanosecond to complete. | |||
The following image depicts the polarization of a single atom. The red, positively-charged nucleus is surrounded by a region of uniform electron density initially. When a positive point charge is placed to the right of the atom, the electron density shifts to the right as the negatively charged electrons are attracted to the positive point charge. The atom becomes an induced dipole as the right side becomes slightly negatively charged and the left becomes positively charged. Note that the positively charged nucleus is not what moves, but the electron density around the nucleus is what shifts to result in this induced dipole. The same thing happens on the molecular level for molecules in an insulator. In the covalent bonds of molecules, the electrons are shared between the atoms with a region of shared electron density around both nuclei. When a point charge is put near a molecule, the electron density shifts in the same way as it would for a single atom, and a dipole is induced as the electrons shift either toward or away from the point charge. | |||
[[File:PolarizationofMolecule.png]] | |||
The polarization of an insulator is just the polarization of several moles of atoms or molecules. This image depicts the effect of a negative point charge placed to the right of an insulator. Every atom or molecule in the insulator will be polarized to create several induced dipoles with the positive end facing the negative point charge. | |||
[[File:PolarizationofNeutralInsulator.png|375 px]] | |||
In addition to being polarized by an external charge, insulators can have their charge. Unlike charges on conductors, this charge is not necessarily evenly distributed throughout the insulator. The image below gives three examples of charge distribution on insulators. The left shows even charge distribution over the outside of the insulator; the middle shows a patch of charge on the outside of the insulator, and the right shows an internal charge in an insulator. Excess charge in patches, as well as internal charge, can also result in polarization of the insulator's atoms or molecules. However, when the charge is evenly distributed, no dipole is induced as this would cause, in this example, the positive ends to point toward the outside while the negative ends point inward toward each other and repel each other; this is an impossible configuration, so the electron clouds remain evenly distributed. Charges on insulators can polarize other materials; you have most likely felt this when touching a piece of plastic with an excess charge on it and feeling your hairs stand on end. This will likely come up in this class in the context of charged insulators polarizing other materials. | |||
[[File:DifferentChargeDistributions.png|700 px]] | |||
'''Testing Resistivity''' | |||
To test the resistivity of an insulator we need to look at the breakdown voltage. The breakdown voltage of an insulator is the minimum voltage required to make a portion of the insulator conductive. This is done by creating a weakened path in the material – a permanent physical or molecular change to the material. The voltage gives the electrons enough energy to be excited. Many will use this to test for the maximum amount of voltage a material can withstand before it completely collapses. | |||
==A Mathematical Model== | ===A Mathematical Model=== | ||
The range of resistivities in various materials vary drastically: a conductor may have a resitivity on the order of <math> 10^{-8} \; \Omega \cdot m </math>, while insulators may have resitivities on orders between <math> 10^{12} </math> and <math> 10^{20} \; \Omega \cdot m </math>. <ref> https://www.britannica.com/science/resistivity </ref> | |||
'''Resistivity''' | |||
Resistivity is the intrinsic property that quantifies how strongly a material opposes the flow of electric current. The units of resistivity are Ohms Meter, and the equation to solve for resistivity is: | Resistivity is the intrinsic property that quantifies how strongly a material opposes the flow of electric current. The units of resistivity are Ohms Meter, and the equation to solve for resistivity is: | ||
| Line 26: | Line 50: | ||
'''''<math>\rho = R \frac{A}{\ell}, \,\!</math>''''' where R is resistance, ''<math>\ell</math>'' is the length of the material and A is the cross sectional area of the specimen. | '''''<math>\rho = R \frac{A}{\ell}, \,\!</math>''''' where R is resistance, ''<math>\ell</math>'' is the length of the material and A is the cross sectional area of the specimen. | ||
To calculate resistivity, the size of the material is taken into account along with the resistance. Many objects can claim to have roughly the same resistance, but by taking | To calculate resistivity, the size of the material is taken into account along with the resistance. Many objects can claim to have roughly the same resistance, but by taking the specific dimensions of the material into account we find the resistivity, which is specific to each material. From the equation, it can be concluded that resistivity is an intrinsic property of a material, allowing it to be similar across all specimens of a material. For example, ceramic will have a much high electrical resistivity than copper, but the resistivity of two ceramic specimens with the same dimensions will be the same. | ||
'''Note: Usually we will use this equation in the form <math>R = \rho \frac{A}{\ell}</math> to solve for resistance based on a known resistivity. Be careful not to confuse resistance and resistivity; the wording in this section is a little tricky.''' | |||
===A Computational Model=== | |||
[https://phet.colorado.edu/sims/html/circuit-construction-kit-dc/latest/circuit-construction-kit-dc_en.html| Circuit Construction] | |||
This simulation is a great way to visualize the difference in electric conductivity in conductors and insulators. Try building a circuit with different materials to see which allow for current to flow and which do not. You can use a circuit of just wires, a battery, and a light bulb as a baseline and try switching out different things for the wire. | |||
[[File:Insulators computational model picture .png|600 px]] | |||
==Examples== | |||
===Simple=== | |||
Material A has a conductivity of 200 <math>S \cdot m^{-1} </math>, where <math>S = \Omega^{-1}</math>, while material B has a resistivity of 30 <math>\Omega \cdot m </math>. Which material is the better insulator? | |||
<div class="toccolours mw-collapsible mw-collapsed" style="width:800px; overflow:auto;"> | |||
<div style="font-weight:bold;line-height:1.6;">Solution</div> | |||
<div class="mw-collapsible-content"> | |||
Since resistivity is the inverse of conductivity, we can convert conductivity to resistivity to see which will be the better insulator. We could also convert resistivity to conductivity, but the first makes more sense because higher resistivity is an indication of a good insulator. | |||
= | <math>200 S \cdot m^{-1} = 5 \cdot 10^{-3} </math>. Therefore, material B is a much better insulator than Material A. | ||
</div></div> | |||
=== | ===Middling=== | ||
You have two capacitors, one filled with insulator A and one filled with insulator B. Insulator A has a dielectric constant of 5, and insulator B has a dielectric constant of 10. Assuming both insulators have the same area, the charge on their plates, and distance between plates; which one would have the greater potential difference across it? | |||
<div class="toccolours mw-collapsible mw-collapsed" style="width:800px; overflow:auto;"> | |||
<div style="font-weight:bold;line-height:1.6;">Solution</div> | |||
<div class="mw-collapsible-content"> | |||
You can read more about potential differences here: [[Potential Difference]]. Since both capacitors have plates with the same charge and area, both will have the same applied electric field. The actual electric field inside capacitor A will be greater because it has a lower dielectric constant. Because of this, we will see a greater potential difference by a factor of 2 across capacitor A. | |||
</div></div> | |||
=== | ===Difficult=== | ||
[[File:Capacitor diagram.png|right|350 px]] | |||
A capacitor consists of 2 plates. Each plate carries a charge of 0.01 C and has an area of 1000 <math>m^2</math>. The area between the two plates is filled with an insulator that has a dielectric constant of 5. To the right is a diagram of the insulator-filled capacitor. | |||
a. Consider a dipole(show below) located within the insulator. Draw 3 arrows corresponding to (1) the applied electric field, <math>\vec {E}_{app}</math>, (2) the electric field due to the dipole, <math>\vec {E}_{d}</math>, and (3) the net electric field. | |||
[[File:Dipole for question.png|150 px]] | |||
b. Calculate the electric field inside the insulator. | |||
<div class="toccolours mw-collapsible mw-collapsed" style="width:800px; overflow:auto;"> | |||
<div style="font-weight:bold;line-height:1.6;">Solution</div> | |||
<div class="mw-collapsible-content"> | |||
a. [[File:Dipole for question answer.png|330 px]] | |||
= | b. <math>\vec {E}_{ins} = \frac{\vec {E}_{app}}{K}</math> | ||
<math>\vec {E}_{app} = \vec {E}_{capacitor} = \frac{Q/A}{ε_0}</math> | |||
<math>\vec {E}_{capacitor} = \frac{0.01/1000}{8.85 \cdot 10^{-12}} = 1.13 \cdot 10^6 \frac{N}{C}</math> | |||
<math>\vec {E}_{ins} = \frac{1.13 \cdot 10^6}{5} = 2.26 \cdot 10^5 \frac{N}{C} </math> | |||
<math>200 S \cdot m^{-1} = 5 \cdot 10^{-3} </math>. Therefore, material B is a much better insulator than Material A. | |||
</div></div> | |||
==Connectedness== | |||
This topic is very connected to my interests. I enjoy learning about the physics and chemistry behind material properties. It amazes me to see how chemical properties such as the number of valence electrons in a material can have such a profound effect on a physical property like conductance. | |||
As a chemical engineer, the topic of insulators is connected to my major. One of the industries I am considering working in is the materials industry. It is important to understand the chemistry behind a material so that you can know how that material will behave in certain applications. | |||
Insulators are used in many different capacities but always for the same two functions: to limit the flow of electric current or heat. A prime example of insulator usage is the plastics and other polymers used to coat wires. Wires touching could cause short-circuiting and fires, so a thin covering of insulating material is nearly always placed around them to help prevent these hazards. This also helps protect wires from other elements; for example, power lines are covered for safety but also for protection from outdoor elements, such as rain, which would act as a conductor and would deteriorate the metal wire. | |||
'''Capacitors''' | |||
Insulators are also used in the space between plates in capacitors. The insulator can take the form of air or a thin piece of plastic or other insulating material. The insulator chosen plays a role in the capacitance of the capacitor based on the dielectric constant, a property of the insulating material. The insulator between the plates ensures charge cannot flow from one plate to the other, which allows the crucial ability of capacitors to charge and discharge. | |||
'''Power lines''' | |||
Typically, these high voltage wires are insulated by air. Insulating materials are only used when the wires are connecting to a pole or support. Insulators are also required where these lines enter buildings and electrical centers. Ceramics (including glass), is the material of choice in building insulators for power lines, and they typically have an outer coat of gloss to prevent the buildup of condensation. | |||
[[File:11.png|400 px]] | |||
[ | |||
'''Antennas''' | |||
Broadcasting antennas are giant high voltage structures, so they must be insulated from the ground and be protected against lightning. Usually, cables are used to break up the voltage and to help prevent short-circuiting. Ceramic insulators are commonly used. The insulator is under compression as opposed to the tension that is seen with powerlines. | |||
== | ==History== | ||
The use of electrical insulators began as soon as people started using electricity. Thomas Edison was awarded a patent in 1892 for creating an electric conductor. This 'electric conductor' consisted of two materials. The first was a cotton-braid mesh that was placed on the wire to separate it from the insulator. The second was a rubber coating. This combination made it safe to begin working with wires. Since then, the application of insulators has become a major part of our daily lives. | |||
== See also == | == See also == | ||
===Further Reading=== | |||
[[Conductivity|Conductivity]] | [[Conductivity|Conductivity]] | ||
| Line 112: | Line 149: | ||
[[Charge Transfer|Charge Transfer]] | [[Charge Transfer|Charge Transfer]] | ||
===External Links=== | |||
[https://www.youtube.com/watch?v=ZgDIX2GOaxQ Khan Academy video] | |||
[https://www.youtube.com/watch?v=7RpyURBNZyU Why do Metals conduct electricity? video] | |||
[https://www.physicsclassroom.com/class/estatics/Lesson-1/Conductors-and-Insulators Conductors and Insulators] | |||
==References== | ==References== | ||
Holtzhausen, J.P. "High Voltage Insulators" (PDF). IDC Technologies. Retrieved 2008-10-17. | |||
Grigsby, Leonard L. (2001). The Electric Power Engineering Handbook. USA: CRC Press. ISBN 0-8493-8578-4 | Grigsby, Leonard L. (2001). The Electric Power Engineering Handbook. USA: CRC Press. ISBN 0-8493-8578-4 | ||
Bakshi, M (2007). Electrical Power Transmission and Distribution. Technical Publications. ISBN 978-81-8431-271-3. | |||
http://www.allaboutcircuits.com/textbook/direct-current/chpt-12/insulator-breakdown-voltage/ | http://www.allaboutcircuits.com/textbook/direct-current/chpt-12/insulator-breakdown-voltage/ | ||
| Line 126: | Line 170: | ||
http://www.techlib.com/reference/insulation.html | http://www.techlib.com/reference/insulation.html | ||
[[Category: Simple Circuits]] | [[Category: Simple Circuits]] | ||
Latest revision as of 19:30, 24 April 2022
Ammar Ladhani Spring 2022


Insulators are characterized by the limited ability of charge to flow through them. In a typical insulator, electrons are bound to individual atoms or molecules, preventing easy flow through the material. Conductors, in contrast, are characterized by the presence of free charges (typically electrons), which can move easily and thus allow charge to flow easily through the material. Metals are the prototypical conductor, with large numbers of electrons in weakly bound valence orbitals. Saltwater also acts as a conductor, since the ions dissolved in the water respond easily to electrical fields, and so transmit current. Typical insulators include structures of organic molecules, which are composed primarily of covalent bonds, and therefore inhibit the easy flow of electrons.
The Main Idea
An insulator is a material that restricts the flow of charges due to an applied electric field. When a charge, such as an electron, is put under an applied field, it will experience a force that causes it to move. In an insulator, however, all electrons are tightly bound to the molecule they belong to; rather than the free-flowing "sea of electrons" in metals. Since there are no free, mobile electrons in an insulator, no charges will move through the material. An applied electric field still causes a force on the electrons in the insulator though, which results in the polarization of the insulator. When an insulator polarizes, the electron orbital will shift, as described in Polarization, resulting in induced dipoles. While the effect of each induced dipole is minuscule, the additive-induced polarization of the whole material can have a large effect.
The classification of a material as an insulator or conductor is determined by its conductivity and resistivity. As described on that page, these are two sides of the same coin, with each being the reciprocal of the other. Perfect insulators are a non-physical idealization, as in any material a small number of charges will still be able to move, especially when a very high voltage is applied. Insulators are ubiquitous in everyday life since if one is working with electricity, one wishes to restrain where it will go. Although the typical insulator we will consider is characterized by the presence of covalent bonds, many other insulating materials exist: air, for example, is an insulator, since it is very difficult for the current to flow through it unaided. In the presence of sufficiently high voltages, this results in lightning (or, on a smaller scale, sparking), in which the air is ionized, producing a viable conducting channel for the current to flow.
Band Theory
Electrons tend to seek the lowest energy state in their configuration, and the highest characteristic state, or band, at which the electrons of an element have filled up is called the Fermi level. Only electrons near the Fermi level are allowed to "jump" to another atom, which is how the electron sea of metals works. Metals have many electrons near their Fermi levels, allowing them to have great conductivity as compared to other materials. The opposite is true for insulators. The amount of electrons in an insulator available for conduction is close to none, meaning a high voltage potential at one end of the insulator will cause little to no change in the electrical structure of the insulator.
The band theory is used to describe the energy levels of valence electrons of atoms. As you may have seen with UV-spectroscopy, electrons for a single atom exist in distinct energy levels; the energy is quantized, meaning the electrons can only exist at specific energy amounts and not in between two steps. For material, the band theory takes into account multiple atoms, which results in a wider energy band/range rather than discrete steps. These bands are the valence band, where all of the valences electrons exist at the ground state, and the conductance band; the gap between these is known as the bandgap. Because the valence shells of atoms in an insulator are full due to either covalent or ionic bonding, the valence state is very stable, and a large amount of energy must be put in to get electrons to jump from the valence band to the conductance band; this means that the bandgap for an insulator is very large. A larger bandgap means a worse conductor. For conductors, the bandgap is zero and electrons can jump straight from the valence band to the conductance band with only a small amount of energy put in. The diagram below demonstrates the band diagram for insulators versus conductors.
Polarization of Insulators
In insulators, all charged particles are tightly bound to the molecules making up the material. When an electric field is applied, the charged particles (electrons) in an insulator shift position slightly but still stay bound to the molecules. The largest distance the charged particles can move is about one atomic diameter, which is [math]\displaystyle{ 1^{-10} }[/math] m. Because the mobile charge is displaced by such a small distance, the polarization happens very quickly. The whole process can generally take less than a nanosecond to complete.
The following image depicts the polarization of a single atom. The red, positively-charged nucleus is surrounded by a region of uniform electron density initially. When a positive point charge is placed to the right of the atom, the electron density shifts to the right as the negatively charged electrons are attracted to the positive point charge. The atom becomes an induced dipole as the right side becomes slightly negatively charged and the left becomes positively charged. Note that the positively charged nucleus is not what moves, but the electron density around the nucleus is what shifts to result in this induced dipole. The same thing happens on the molecular level for molecules in an insulator. In the covalent bonds of molecules, the electrons are shared between the atoms with a region of shared electron density around both nuclei. When a point charge is put near a molecule, the electron density shifts in the same way as it would for a single atom, and a dipole is induced as the electrons shift either toward or away from the point charge.
The polarization of an insulator is just the polarization of several moles of atoms or molecules. This image depicts the effect of a negative point charge placed to the right of an insulator. Every atom or molecule in the insulator will be polarized to create several induced dipoles with the positive end facing the negative point charge.
In addition to being polarized by an external charge, insulators can have their charge. Unlike charges on conductors, this charge is not necessarily evenly distributed throughout the insulator. The image below gives three examples of charge distribution on insulators. The left shows even charge distribution over the outside of the insulator; the middle shows a patch of charge on the outside of the insulator, and the right shows an internal charge in an insulator. Excess charge in patches, as well as internal charge, can also result in polarization of the insulator's atoms or molecules. However, when the charge is evenly distributed, no dipole is induced as this would cause, in this example, the positive ends to point toward the outside while the negative ends point inward toward each other and repel each other; this is an impossible configuration, so the electron clouds remain evenly distributed. Charges on insulators can polarize other materials; you have most likely felt this when touching a piece of plastic with an excess charge on it and feeling your hairs stand on end. This will likely come up in this class in the context of charged insulators polarizing other materials.
Testing Resistivity
To test the resistivity of an insulator we need to look at the breakdown voltage. The breakdown voltage of an insulator is the minimum voltage required to make a portion of the insulator conductive. This is done by creating a weakened path in the material – a permanent physical or molecular change to the material. The voltage gives the electrons enough energy to be excited. Many will use this to test for the maximum amount of voltage a material can withstand before it completely collapses.
A Mathematical Model
The range of resistivities in various materials vary drastically: a conductor may have a resitivity on the order of [math]\displaystyle{ 10^{-8} \; \Omega \cdot m }[/math], while insulators may have resitivities on orders between [math]\displaystyle{ 10^{12} }[/math] and [math]\displaystyle{ 10^{20} \; \Omega \cdot m }[/math]. [1]
Resistivity
Resistivity is the intrinsic property that quantifies how strongly a material opposes the flow of electric current. The units of resistivity are Ohms Meter, and the equation to solve for resistivity is:
[math]\displaystyle{ \rho = R \frac{A}{\ell}, \,\! }[/math] where R is resistance, [math]\displaystyle{ \ell }[/math] is the length of the material and A is the cross sectional area of the specimen.
To calculate resistivity, the size of the material is taken into account along with the resistance. Many objects can claim to have roughly the same resistance, but by taking the specific dimensions of the material into account we find the resistivity, which is specific to each material. From the equation, it can be concluded that resistivity is an intrinsic property of a material, allowing it to be similar across all specimens of a material. For example, ceramic will have a much high electrical resistivity than copper, but the resistivity of two ceramic specimens with the same dimensions will be the same.
Note: Usually we will use this equation in the form [math]\displaystyle{ R = \rho \frac{A}{\ell} }[/math] to solve for resistance based on a known resistivity. Be careful not to confuse resistance and resistivity; the wording in this section is a little tricky.
A Computational Model
This simulation is a great way to visualize the difference in electric conductivity in conductors and insulators. Try building a circuit with different materials to see which allow for current to flow and which do not. You can use a circuit of just wires, a battery, and a light bulb as a baseline and try switching out different things for the wire.
Examples
Simple
Material A has a conductivity of 200 [math]\displaystyle{ S \cdot m^{-1} }[/math], where [math]\displaystyle{ S = \Omega^{-1} }[/math], while material B has a resistivity of 30 [math]\displaystyle{ \Omega \cdot m }[/math]. Which material is the better insulator?
Since resistivity is the inverse of conductivity, we can convert conductivity to resistivity to see which will be the better insulator. We could also convert resistivity to conductivity, but the first makes more sense because higher resistivity is an indication of a good insulator.
[math]\displaystyle{ 200 S \cdot m^{-1} = 5 \cdot 10^{-3} }[/math]. Therefore, material B is a much better insulator than Material A.
Middling
You have two capacitors, one filled with insulator A and one filled with insulator B. Insulator A has a dielectric constant of 5, and insulator B has a dielectric constant of 10. Assuming both insulators have the same area, the charge on their plates, and distance between plates; which one would have the greater potential difference across it?
You can read more about potential differences here: Potential Difference. Since both capacitors have plates with the same charge and area, both will have the same applied electric field. The actual electric field inside capacitor A will be greater because it has a lower dielectric constant. Because of this, we will see a greater potential difference by a factor of 2 across capacitor A.
Difficult
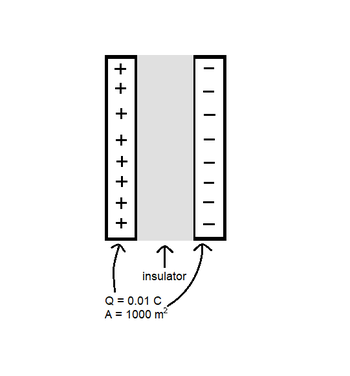
A capacitor consists of 2 plates. Each plate carries a charge of 0.01 C and has an area of 1000 [math]\displaystyle{ m^2 }[/math]. The area between the two plates is filled with an insulator that has a dielectric constant of 5. To the right is a diagram of the insulator-filled capacitor.
a. Consider a dipole(show below) located within the insulator. Draw 3 arrows corresponding to (1) the applied electric field, [math]\displaystyle{ \vec {E}_{app} }[/math], (2) the electric field due to the dipole, [math]\displaystyle{ \vec {E}_{d} }[/math], and (3) the net electric field.
b. Calculate the electric field inside the insulator.
b. [math]\displaystyle{ \vec {E}_{ins} = \frac{\vec {E}_{app}}{K} }[/math]
[math]\displaystyle{ \vec {E}_{app} = \vec {E}_{capacitor} = \frac{Q/A}{ε_0} }[/math]
[math]\displaystyle{ \vec {E}_{capacitor} = \frac{0.01/1000}{8.85 \cdot 10^{-12}} = 1.13 \cdot 10^6 \frac{N}{C} }[/math]
[math]\displaystyle{ \vec {E}_{ins} = \frac{1.13 \cdot 10^6}{5} = 2.26 \cdot 10^5 \frac{N}{C} }[/math]
[math]\displaystyle{ 200 S \cdot m^{-1} = 5 \cdot 10^{-3} }[/math]. Therefore, material B is a much better insulator than Material A.
Connectedness
This topic is very connected to my interests. I enjoy learning about the physics and chemistry behind material properties. It amazes me to see how chemical properties such as the number of valence electrons in a material can have such a profound effect on a physical property like conductance.
As a chemical engineer, the topic of insulators is connected to my major. One of the industries I am considering working in is the materials industry. It is important to understand the chemistry behind a material so that you can know how that material will behave in certain applications.
Insulators are used in many different capacities but always for the same two functions: to limit the flow of electric current or heat. A prime example of insulator usage is the plastics and other polymers used to coat wires. Wires touching could cause short-circuiting and fires, so a thin covering of insulating material is nearly always placed around them to help prevent these hazards. This also helps protect wires from other elements; for example, power lines are covered for safety but also for protection from outdoor elements, such as rain, which would act as a conductor and would deteriorate the metal wire.
Capacitors
Insulators are also used in the space between plates in capacitors. The insulator can take the form of air or a thin piece of plastic or other insulating material. The insulator chosen plays a role in the capacitance of the capacitor based on the dielectric constant, a property of the insulating material. The insulator between the plates ensures charge cannot flow from one plate to the other, which allows the crucial ability of capacitors to charge and discharge.
Power lines
Typically, these high voltage wires are insulated by air. Insulating materials are only used when the wires are connecting to a pole or support. Insulators are also required where these lines enter buildings and electrical centers. Ceramics (including glass), is the material of choice in building insulators for power lines, and they typically have an outer coat of gloss to prevent the buildup of condensation.
Antennas
Broadcasting antennas are giant high voltage structures, so they must be insulated from the ground and be protected against lightning. Usually, cables are used to break up the voltage and to help prevent short-circuiting. Ceramic insulators are commonly used. The insulator is under compression as opposed to the tension that is seen with powerlines.
History
The use of electrical insulators began as soon as people started using electricity. Thomas Edison was awarded a patent in 1892 for creating an electric conductor. This 'electric conductor' consisted of two materials. The first was a cotton-braid mesh that was placed on the wire to separate it from the insulator. The second was a rubber coating. This combination made it safe to begin working with wires. Since then, the application of insulators has become a major part of our daily lives.
See also
Further Reading
External Links
Why do Metals conduct electricity? video
References
Holtzhausen, J.P. "High Voltage Insulators" (PDF). IDC Technologies. Retrieved 2008-10-17.
Grigsby, Leonard L. (2001). The Electric Power Engineering Handbook. USA: CRC Press. ISBN 0-8493-8578-4
Bakshi, M (2007). Electrical Power Transmission and Distribution. Technical Publications. ISBN 978-81-8431-271-3.
http://www.allaboutcircuits.com/textbook/direct-current/chpt-12/insulator-breakdown-voltage/
http://www.engineeringtoolbox.com/resistivity-conductivity-d_418.html