Specific Heat: Difference between revisions
No edit summary |
|||
| (128 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
''' | ==Main Idea== | ||
[[File:Airspecific.PNG|right|250px]] | |||
The '''Specific Heat Capacity''' of a substance, also known as the Specific Heat, is defined as the amount of energy required to raise the temperature of one gram of the substance by one degree Celsius. '''Specific Heat Capacity''' is important, as it can determine the thermal interaction a material has with other materials. We can test the validity of models with '''Specific Heat Capacity''' since it is experimentally measurable. Also, the '''Specific Heat Capacity''' of a substance depends on its phase (solid, liquid, gas, or plasma) and its molecular structure. At its core, '''Specific Heat Capacity''' is based on the idea that different materials will store Heat differently, due to varying masses, molecular structure, and number of particles per unit mass. Finally, '''Specific Heat Capacity''' is an intensive property, meaning that the amount of the substance does not affect this property, only the composition of the substance does. It is worth noting the '''Specific Heat Capacity''' of a substance usually changes slightly with Temperature, as can be seen in the table for air on the right. However, in our studies, we will consider it as a constant. | |||
Specific | There are a few quantities that are closely related to the '''Specific Heat Capacity''' of a substance: | ||
*'''Heat Capacity''': | |||
**The concept of Heat Capacity is an extensive property (dependent on how much of the substance is present) that is integral to understanding how the Temperature of a substance rises and falls. Heat Capacity is the ratio of energy added or removed from a substance to the Temperature change observed in that substance. Typically, heat capacities are expressed in terms of the amount of heat (kJ, J, or kCal) that needs to be added to raise the temperature of a substance by 1 degree (Celsius, Fahrenheit, Kelvin) | |||
**'''Specific Heat Capacity''' is an intensive property as mentioned previously. Conversely, Heat Capacity is an extensive property, meaning it does depend on the amount of substance present. In other words, the '''Specific Heat Capacity''' for 1 kg of iron is the same as that of 100 kg of iron, but the Heat Capacity would be different for these two amounts, since it takes more Heat to raise 100 kg of iron by one degree than it does to raise 1 kg of iron by one degree. To determine the Heat Capacity of a quantity of substance, simply multiply the '''Specific Heat Capacity''' by the amount of substance present | |||
[[File:specificheatmetals.jpg|300px|right]] | |||
:*Typical units of Heat Capacities are J/g, kJ/kg, and BTU/lb-mass. The SI unit of Heat Capacity is J/g | |||
*'''Molar Heat Capacity''': | |||
**Molar Heat Capacity is similar to '''Specific Heat Capacity'''. It expresses the amount of Heat required to raise one gram-mole of a substance by one degree Celsius | |||
**It is expressed in J/mol-°C. The Molar Heat Capacity of water is 75.37 J/mol-°C | |||
[[ | ===Mathematical Model=== | ||
There are a few ways to find the '''Specific Heat Capacity''' of a material or system, such as the [[Thermal Energy]] equation, the Law of Dulong and Petit, or the Einstein-Debye Model. | |||
====Thermal Energy Equation==== | |||
The relationship between the Heat and Temperature change of a system is best defined by the '''Specific Heat''' constant <math>C</math> in the equation below: | |||
T | :::<math> \Delta Q = mC \Delta T</math> | ||
For a review of the meaning of this equation, view [[Thermal Energy#Mathematical Model| Thermal Energy Equation]]. | |||
It is important to note this equation does not apply if a phase change occurs (say from a liquid state to a gaseous state). | |||
Rearranging this equation gives us a way to calculate the '''Specific Heat Capacity''' of the system: | |||
:::<math>C = \frac{\Delta Q}{m \Delta T} = \frac{1}{m}\frac{dQ}{dT}</math> | |||
We can in fact see a dependence on the Temperature of the system here. We can rewrite this as: | |||
:::<math>Q = m \int_{T_1}^{T_2} C \ dT</math> | |||
If we know the dependence of the '''Specific Heat Capacity''' on Temperature, we can solve for the change in Thermal Energy. | |||
====Law of Dulong and Petit==== | |||
The Law of Dulong and Petit is a Thermodynamic law discovered in 1819 by the French physicists Pierre Louis Dulong and Alexis Thérèse Petit. It yields the expression for the Molar Specific Heat Capacity of certain chemical elements. They found, through experiments, that the Mass Specific Heat Capacity for many elements was close to a constant value, after it had been adjusted to reflect the relative atomic weight of the element. | |||
Basically, Dulong and Petit found that the '''Specific Heat Capacity''' of a mole of numerous solid elements is about 3R, where R is the universal gas constant. Dulong and Petit were unaware of the relationship to R, since it had not yet been defined. The value of 3R is about <math>25 \ \frac{J}{mol \cdot K}</math>, and Dulong and Petit found that this was the approximate Molar Specific Heat Capacity of some solid elements per mole of atoms they contained. | |||
''' | :For example, The '''Specific Heat Capacity''' of copper is <math>0.385 \ \frac{J}{g \cdot K}</math>. The '''Specific Heat Capacity''' of lead is <math>0.128 \ \frac{J}{g \cdot K}</math>. Why are the values so different in these two metals? Did you notice that they are expressed as energy per unit mass? If you express each as energy per mole, they are actually very similar. The Law of Dulong and Petit addresses this similarity in molar specific heats. It can be accounted for by applying equipartition of energy to the atoms of solids: | ||
'' | ::<math>\text{Energy per mole} = 3kTN_{A}</math>, where | ||
:::<math>k = </math> Boltzmann's constant<br> | |||
:::<math>T = </math> Temperature in Kelvin<br> | |||
:::<math>N_{A} = </math> Avogadro's Number | |||
::<math>\text{The Law of Dulong and Petit:} \quad C = \frac{\partial}{\partial T}\left(3kTN_{a} \right) = \frac{3kN_{a}}{mol} = 24.94 \ \frac{J}{mol \cdot K}</math> | |||
:To see the Molar '''Specific Heat Capacity''', we multiply the Mass '''Specific Heat Capacity''' by the mass per mole of the substance. This molar basis, the Molar '''Specific Heat Capacity''' of copper and lead, are as follows: | |||
::<math>\text{Copper:} \ C_{c} \times \left(\frac{M}{mol}\right)_{c} = 0.385 \times 63.546 = 24.5 \ \frac{J}{mol \cdot K}</math> | |||
::<math>\text{Lead:} \ C_{l} \times \left(\frac{M}{mol}\right)_{l} = 0.128 \times 207.2 = 26.5 \ \frac{J}{mol \cdot K}</math> | |||
:Here are a few more examples: | |||
::<math>\text{Aluminum:} \ 24.3 \ \frac{J}{mol \cdot K}</math> | |||
::<math>\text{Gold:} \ 25.6 \ \frac{J}{mol \cdot K}</math> | |||
::<math>\text{Silver:} \ 24.9 \ \frac{J}{mol \cdot K}</math> | |||
::<math>\text{Zinc:} \ 25.2 \ \frac{J}{mol \cdot K}</math> | |||
====Einstein-Debye Model==== | |||
Einstein and Debye each developed a model for '''Specific Heat Capacity''' separately. Einstein's model stated that low energy excitation of a solid material was caused by the oscillation of a single atom, whereas Debye's model stated that phonons or collective modes iterating through a material caused excitations. However, these two models are able to be put together to find the '''Specific Heat Capacity''' given by the following formula: | |||
== | :::::::::::<math>C_{metal} = C_{electron} + C_{phonon} = \frac{{\pi}^2 N {k_{B}}^2}{2E_{f}}T + \frac{12{\pi}^4 N k_{b}}{5{T_{D}}^3}T^3</math> | ||
For low temperatures, Einstein and Debye found that the Law of Dulong and Petit was not applicable. At lower temperatures, it was found that atomic interactions were deemed significant in calculating the Molar Specific Heat Capacity of an object: | |||
[[File: Einstein Debye Graphs.gif|center|600px]] | |||
According to the Einstein Debye Model for Copper and Aluminum, specific heat varies a lot at lower temperatures and goes much below the Dulong-Petit Model. This is due to increased effects on specific heat by interatomic forces. However, for very high temperatures, the Einstein-Debye Model cannot be used. In fact, at high temperatures, Einstein's expression of specific heat reduces to the Dulong-Petit mathematical expression. | |||
The Einstein Debye Equation is below: | |||
:::::::::::<math>C = \frac{\partial E}{\partial T} = \frac{3N_{A}k_{B}\left(\frac{hv}{k_{B}T}\right)^2 e^{hv/k_{B}T}}{\left(e^{hv/k_{B}T} - 1 \right)^2} \ mole^{-1}</math> | |||
For high temperatures it may be reduced like this: | |||
:::::::::::<math>C \approx \frac{3N_{A}k_{B}\left(\frac{hv}{k_{B}T}\right)^2 \left(1 + \frac{hv}{k_{B}T} \right)}{\left(\frac{hv}{k_{B}T} \right)^2} \ mole^{-1}</math> | |||
:::::::::::<math>C \approx 3N_{A}k_{B}\left(1 + \frac{hv}{k_{B}T} \right) mole^{-1} \approx 3N_{A}k_{B} \ mole^{-1}</math> | |||
===Computational Model=== | |||
:'''Insert Model Here''' | |||
==Examples== | |||
To the right is a table containing the '''Specific Heat Capacity''' for a variety of atoms that will be useful for the examples. | |||
[[File:Specific-heat-capacity.PNG|right|400px]] | |||
===Simple=== | |||
350 grams of an unknown substance is heated from 22ºC to 173ºC with 34,700 Joules of energy. There is no phase change. | |||
:'''a) What is the Specific Heat Capacity''' (<math>C</math>) '''of this unknown substance?''' | |||
::Applying the main equation of our [[Specific Heat#Mathematical Model| Mathematical Model]] solves this in one step" | |||
:::<math>C = \frac{\Delta Q}{m \Delta T}</math> | |||
::We know the value of everything in this equation except <math>C</math>: | |||
:::<math>C = \frac{34,700}{350 \times (173 - 22)} = 0.66 \ \frac{J}{gºC}</math> | |||
:'''b) What is the Heat Capacity''' (<math>H</math>) '''of this unknown substance?''' | |||
''' | ::To find the Heat Capacity of a sample of a substance, we must multiply the '''Specific Heat Capacity''' of the substance by the mass of the sample: | ||
:::<math>H = mC = 350 \times 0.66 = 231 \ \frac{J}{ºC}</math> | |||
===Middling=== | |||
1,200 grams of coffee is sitting on a table is at a Temperature of <math>T_{co_{0}} = 93ºC</math>. Assume the '''Specific Heat Capacity''' of coffee is <math>4.12 \ \frac{J}{gºC}</math>. The coffee is mixed with 55.3 grams of cream at <math>T_{cr_{0}} = 5ºC</math>. The '''Specific Heat Capacity''' of creamer is <math>3.8 \ \frac{J}{gºC}</math>. | |||
:'''a) What is the final temperature of the mixture''' (<math>T_f</math>) ''', assuming that no Thermal Energy is lost to the surroundings, after the system reaches Thermal Equilibrium?''' | |||
::Since no energy is lost to the surroundings, we can manipulate the energy principle as follows: | |||
:::<math>\Delta E_{system} + \Delta E_{surroundings} = 0</math> | |||
:::<math>E_{system_{f}} - E_{system_{0}} = 0</math> | |||
:::<math>E_{system_{f}} = E_{system_{0}}</math> | |||
:::<math>E_{co_{f}} + E_{cr_{f}} = E_{co_{0}} + E_{cr_{0}}</math> '''(1)''' | |||
::We see that the final energy of the system must be equal to the initial energy of the system, the system being the coffee and the creamer mixture. All we know is that a Temperature change will occur in each part of the system. This change in Thermal Energy is proportional to the change in Temperature by: | |||
:::<math>\Delta Q = mC \Delta T</math> | |||
::or: | |||
:::<math>Q_{f} - Q_{0} = mCT_{f} - mCT_{0}</math> | |||
::or: | |||
:::<math>Q_{f} = mCT_{f} \quad Q_{0} = mCT_{0}</math> '''(2)''' | |||
::The change in energy of the system will be due to only this change in Temperature: | |||
= | :::<math>\Delta E_{system} = \Delta Q_{system}</math> '''(3)''' | ||
::From '''1''', '''2''', and '''3''', we see: | |||
:::<math>E_{system_{f}} - E_{system_{0}} = Q_{system_{f}} - Q_{system_{0}} = 0</math> | |||
:::<math>(E_{co_{f}} + E_{cr_{f}}) - (E_{co_{0}} + E_{cr_{0}}) = (Q_{co_{f}} + Q_{cr_{f}}) - (Q_{co_{0}} + Q_{cr_{0}}) = 0</math> | |||
:::<math>(Q_{co_{f}} + Q_{cr_{f}}) - (Q_{co_{0}} + Q_{cr_{0}}) = (m_{co}C_{co}T_{co_{f}} + m_{cr}C_{cr}T_{cr_{f}}) - (m_{co}C_{co}T_{co_{0}} + m_{cr}C_{cr}T_{cr_{0}}) = 0</math> '''(4)''' | |||
::Note, <math>T_{co_{f}} = T_{f} = T_{cr_{f}}</math>, since the system is allowed to reach Thermal Equilibrium, reducing '''4''' to: | |||
:::<math>(m_{co}C_{co}T_{f} + m_{cr}C_{cr}T_{f}) - (m_{co}C_{co}T_{co_{0}} + m_{cr}C_{cr}T_{cr_{0}}) = 0</math> | |||
:::<math>(m_{co}C_{co} + m_{cr}C_{cr})T_{f} - (m_{co}C_{co}T_{co_{0}} + m_{cr}C_{cr}T_{cr_{0}}) = 0</math> | |||
:::<math>T_{f} = \frac{m_{co}C_{co}T_{co_{0}} + m_{cr}C_{cr}T_{cr_{0}}}{m_{co}C_{co} + m_{cr}C_{cr}}</math> | |||
::Plugging in values gives: | |||
:::<math>T_{f} = \frac{(1,200 \times 4.12 \times 93) + (55.3 \times 3.8 \times 5)}{(1,200 \times 4.12) + (55.3 \times 3.8)} = 89.41ºC</math> | |||
===Difficult=== | |||
At low temperatures, the '''Specific Heat Capacities''' of solids are typically proportional to <math>T^3</math>. The first understanding of this behavior was due to the Dutch physicist Peter Debye, who in 1912, treated atomic oscillations with the quantum theory that Max Planck had recently used for radiation. For instance, a good approximation for the '''Specific Heat Capacity''' of salt, NaCl, is <math>C = 3.33 \times 10^4 \ \frac{J}{kg \cdot K}\left(\frac{T}{321K}\right)^3</math>. The constant <math>321 K</math> is called the Debye temperature of NaCl, <math>\theta_D</math>, and the formula works well when <math>T < 0.04\theta_D</math>. | |||
:'''a) Using this formula, how much Heat is required to raise the Temperature of 24.0 g of NaCl from''' <math>5 K \ \text{to} \ 15 K</math> '''?''' | |||
[[ | ::We see there is a dependence on Temperature in our '''Specific Heat Capacity'''. Hence, we should use the last equation in our [[Specific Heat#Thermal Energy Equation| Thermal Energy Equation Section]]: | ||
:::<math>Q = m \int_{T_1}^{T_2} C \ dT</math> | |||
::In this instance, the following quantities are defined for us: | |||
= | :::<math>m = 24g</math> | ||
:::<math>T_1 = 5K</math> | |||
:::<math>T_2 = 15K</math> | |||
:::<math>C = 3.33 \times 10^4 \ \frac{J}{kg \cdot K}\left(\frac{T}{321K} \right)^3</math> | |||
::We have all the info we need, so let's go ahead and solve: | |||
:::<math>Q = 0.024 \int_{5}^{15} 3.33 \times 10^4 \times \left(\frac{T}{321} \right)^3 \ dT</math> | |||
:::<math>Q = \frac{0.024 \times 3.33 \times 10^4}{321^3 \times 4}\left[T^4\right]_{5}^{15}</math> | |||
:::<math>Q = \left(6.04 \times 10^{-4} \ \frac{J}{K^4}\right)\left(15^4 - 5^4 \right)</math> | |||
:::<math>Q = 30.2 \ J</math> | |||
==Connectedness== | |||
The '''Specific Heat Capacity''' most commonly known is the '''Specific Heat Capacity''' of water, which is about 4.12 J/g°C or 1 calorie/g°C. The specific heat of water is higher than any other common substance. Water has a very large specific heat on a per-gram basis, meaning that it takes a lot more added heat to cause a change in its temperature. Since the specific heat of water is so high, water can be used for temperature regulation. Due to the difference in atomic structures, the specific heat per gram of water is much higher than that of a metal substance. It is possible to predict the specific heat of any material, as long as you know about its atomic structure, as a rise in temperature is the increase in energy at the atomic level of substances. Generally, it is more more useful to compare molar specific heats of substances. | |||
It is easy to notice that water's specific heat capacity is much larger than anything else, but why? The answer is due to water's intermolecular forces. Since a water molecule is made up of one oxygen atom(negative charge) and two hydrogen atoms(slight positive charges), water has hydrogen bonds which result in the "sticking" of water molecules. Because of these hydrogen bonds, it requires a lot of energy to heat up water molecules, because not only do you have to use energy to increase the movement of the particle, but also to break the hydrogen bonds. As a result water has a high specific heat capacity because it takes a lot of energy to break the hydrogen bonds. | |||
[[File: | [[File:jedandva.jpg.png|center]] | ||
This is not an exclusive trait to water, however. The stronger the intermolecular forces of an object, generally the higher the specific heat capacity. Traditionally, gases and liquids have a higher specific heat capacity than solids. In addition, specific heat capacity is also related to the amount of kinetic energy possible in a molecule. Therefore, molecules with more available movement(liquids and gases), there is more room for the heat to "go". Because it is related to kinetic energy, as the external temperature approaches absolute zero, so does specific heat capacity. | |||
But why is this important? | |||
A large body of water can absorb and store a huge amount of heat from the sun in the daytime, such as during summer, while only warming up a few degrees. During night and Winter, the gradually cooling water can warm the air. This is the reason coastal areas generally have milder climates than inland rtegions. The high specific heat of water also tends to stabilize ocean temperatures, creating a favorable environment for marine life. Thus because of its high specific heat, the water that covers most of Earth keeps temperature fluctuations on land and in water within limits that permit life. Also, because organisms are primarily made of water, they are more able to resist changes in their own temperature than if they were made of a liquid with a lower specific heat. | |||
Specific heat and Thermodynamics are used often in chemistry, nuclear engineering, aerodynamics, and mechanical engineering. It is also used in everyday life in the radiator and cooling system of a car. | |||
Specific heat can have a lot to do with prosthetic manufacturing, which is a focus in Biomedical Engineering. Prosthetics materials must be durable and easy to manipulate in a normal range of temperatures. In order to created medical devices, specific heats must be known, especially for welding or molding things, which require a specific temperature to be effective. At higher temperatures, the Dulong-Petit law must be used to calculate the specific heat of an object. Especially for solid metal objects, which would be used in prosthetics, Dulong-Petit is very useful. | Specific heat can have a lot to do with prosthetic manufacturing, which is a focus in Biomedical Engineering. Prosthetics materials must be durable and easy to manipulate in a normal range of temperatures. In order to created medical devices, specific heats must be known, especially for welding or molding things, which require a specific temperature to be effective. At higher temperatures, the Dulong-Petit law must be used to calculate the specific heat of an object. Especially for solid metal objects, which would be used in prosthetics, Dulong-Petit is very useful. | ||
| Line 221: | Line 218: | ||
Have you ever noticed that sand on the beach can burn your feet but the ocean water is cool and refreshing? Sand has a lower specific heat than ocean water. So when the sun is beating down, the temperature of the land increases faster than that of the sea. | Have you ever noticed that sand on the beach can burn your feet but the ocean water is cool and refreshing? Sand has a lower specific heat than ocean water. So when the sun is beating down, the temperature of the land increases faster than that of the sea. | ||
Insulation is made of materials with high specific heat so that they won't change temperature easily. For example, wood has a high specific heat. A wooden house helps keep the inside cooler during summer because it requires lots of heat to change its temperature. Builders can choose certain materials which allows us to build houses for specific locations and altitudes. | Insulation is made of materials with high specific heat so that they won't change temperature easily. For example, wood has a high specific heat. A wooden house helps keep the inside cooler during summer because it requires lots of heat to change its temperature. Builders can choose certain materials which allows us to build houses for specific locations and altitudes. | ||
==History== | |||
[[File:jbzvezda.jpg|right]] | |||
Dr. Joseph Black, of the University of Glasgow, was first credited with developing the concept of latent heat and '''Specific Heat Capacity''' in the mid 18th century. This allowed the study of Thermodynamics to be further looked in to. Before '''Specific Heat Capacity''' was known, scientists referred to Heat as some sort of invisible liquid. Black, while studying super-cooled water, noticed that when shaken, it instantly turned into ice. This lead him to the concept of "stored Heat," in that shaking it released some form of Heat. This was further developed into the idea that different substances responded to Heat changes differently. He performed an experiment by placing ice and super-cooled water in a room, and the water rapidly rose in temperature while the ice did not. This implied that more Heat was required to raise the Temperature of water than of ice. Black claimed, "If the complete change of ice and snow into water required only the further addition of a very small quantity of heat, the mass, though of considerable size, ought all to be melted in a few minutes or seconds more. Were this really the case, the consequences would be dreadful." After the establishment of the idea of '''Specific Heat Capacity''' and latent heat, scientists began to think of Heat as a system's change in internal energy. This is very important as the concept of '''Specific Heat Capacity''' has helped lead to the vast development of the field of Thermodynamics. | |||
==See also== | |||
[ | ===Further reading=== | ||
*[[Kinds of Matter]]<br> | |||
[ | *[[Boiling Point]]<br> | ||
*[[Melting Point]]<br> | |||
[ | *[[Thermal Energy]]<br> | ||
*[[First Law of Thermodynamics]]<br> | |||
[ | *[[Second Law of Thermodynamics and Entropy]]<br> | ||
*[[Internal Energy]]<br> | |||
[ | *[[Temperature]]<br> | ||
*[[Change of State]]<br> | |||
[ | *[https://engineering.ucsb.edu/~shell/che110a/heatcapacitycalculations.pdf Entropy and Enthalpy Calculations]<br> | ||
*Elementary Principles of Chemical Processes (3rd Edition) By: Richard M. Felder & Ronald M. Rousseau<br> | |||
[ | *Encyclopædia Britannica, 2015, "Heat capacity"<br> | ||
*Biology, 7th Edition by Neil A. Campbell and Jane B. Reece<br> | |||
===External links=== | |||
*[http://www.wisegeek.org/what-is-specific-heat.htm WiseGeek.org]<br> | |||
*[https://www.khanacademy.org/science/biology/water-acids-and-bases/water-as-a-solid-liquid-and-gas/v/specific-heat-of-water KhanAcademy.org]<br> | |||
*[https://en.wikipedia.org/wiki/Heat_capacity Wikipedia: Heat Capacity]<br> | |||
*[http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/spht.html HyperPhysics Specific Heat]<br> | |||
*[https://en.wikipedia.org/wiki/Heat_equation Wikipedia: Heat Equation]<br> | |||
*[http://oceanservice.noaa.gov/education/pd/oceans_weather_climate/media/specific_heat.swf Specific Heat Simulation]<br> | |||
==References== | ==References== | ||
*[https://cnx.org/contents/eg-XcBxE@16.7:ElavTzP_@6/1-4-Heat-Transfer-Specific-Heat-and-Calorimetry| OpenStax Vol 2 Heat Transfer, Specific Heat, and Calorimetry]<br> | |||
*[http://hyperphysics.phy-astr.gsu.edu/hbase/emcon.html#emcon HyperPhysics Concepts]<br> | |||
*[http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/spht.html HyperPhysics Specific Heat]<br> | |||
*[http://scienceworld.wolfram.com/physics/SpecificHeat.html Eric Weisstein's World of Physics: Specific Heat]<br> | |||
*[http://www.wikihow.com/Calculate-Specific-Heat WIkiHow: How to Calculate Specific Heat]<br> | |||
http://hyperphysics.phy-astr.gsu.edu/hbase/ | *[https://www.khanacademy.org/ KhanAcademy.org]<br> | ||
*[http://www.one-school.net/Malaysia/UniversityandCollege/SPM/revisioncard/physics/heat/heatcapacityapplication.html Applications of Specific Heat]<br> | |||
http://hyperphysics.phy-astr.gsu.edu/hbase/ | *[http://brainly.in/question/40990 Uses of Specific Heat]<br> | ||
*[http://www.tutorvista.com/content/physics/physics-iii/heat-and-thermodynamics/dulong-and-petit-law.php Law of Dulong and Petit]<br> | |||
http://scienceworld.wolfram.com/physics/SpecificHeat.html | *[http://faculty.uca.edu/saddison/ThermalPhysics/Heat%20Capacity.pdf| Heat Capacity, Specific Heat, and Enthalpy]<br> | ||
*[http://physics.tutorcircle.com/heat/specific-heat.html| Table of Specific Heats]<br> | |||
http://www.wikihow.com/Calculate-Specific-Heat | *[http://water.usgs.gov/edu/heat-capacity.html Heat Capacity and Water]<br> | ||
*[https://www.aps.org/publications/apsnews/201204/physicshistory.cfm Joseph Black and Latent Heat]<br> | |||
https://www.khanacademy.org/ | *Introduction to Chemical Engineering Thermodynamics Seventh Edition. J. M. Smith, H. C. Van Ness, Michael M. Abbott<br> | ||
*Matter & Interactions Vol I. Chabay Sherwood<br> | |||
http://www.one-school.net/Malaysia/UniversityandCollege/SPM/revisioncard/physics/heat/heatcapacityapplication.html | |||
http://brainly.in/question/40990 | |||
http://www.tutorvista.com/content/physics/physics-iii/heat-and-thermodynamics/dulong-and-petit-law.php | |||
http:// | |||
http:// | |||
https://www. | |||
Introduction to Chemical Engineering Thermodynamics Seventh Edition. J. M. Smith, H. C. Van Ness, Michael M. Abbott | |||
Latest revision as of 08:48, 2 August 2019
Main Idea

The Specific Heat Capacity of a substance, also known as the Specific Heat, is defined as the amount of energy required to raise the temperature of one gram of the substance by one degree Celsius. Specific Heat Capacity is important, as it can determine the thermal interaction a material has with other materials. We can test the validity of models with Specific Heat Capacity since it is experimentally measurable. Also, the Specific Heat Capacity of a substance depends on its phase (solid, liquid, gas, or plasma) and its molecular structure. At its core, Specific Heat Capacity is based on the idea that different materials will store Heat differently, due to varying masses, molecular structure, and number of particles per unit mass. Finally, Specific Heat Capacity is an intensive property, meaning that the amount of the substance does not affect this property, only the composition of the substance does. It is worth noting the Specific Heat Capacity of a substance usually changes slightly with Temperature, as can be seen in the table for air on the right. However, in our studies, we will consider it as a constant.
There are a few quantities that are closely related to the Specific Heat Capacity of a substance:
- Heat Capacity:
- The concept of Heat Capacity is an extensive property (dependent on how much of the substance is present) that is integral to understanding how the Temperature of a substance rises and falls. Heat Capacity is the ratio of energy added or removed from a substance to the Temperature change observed in that substance. Typically, heat capacities are expressed in terms of the amount of heat (kJ, J, or kCal) that needs to be added to raise the temperature of a substance by 1 degree (Celsius, Fahrenheit, Kelvin)
- Specific Heat Capacity is an intensive property as mentioned previously. Conversely, Heat Capacity is an extensive property, meaning it does depend on the amount of substance present. In other words, the Specific Heat Capacity for 1 kg of iron is the same as that of 100 kg of iron, but the Heat Capacity would be different for these two amounts, since it takes more Heat to raise 100 kg of iron by one degree than it does to raise 1 kg of iron by one degree. To determine the Heat Capacity of a quantity of substance, simply multiply the Specific Heat Capacity by the amount of substance present
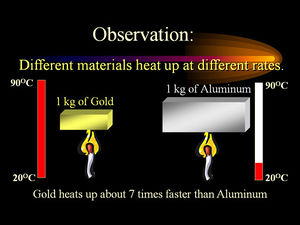
- Typical units of Heat Capacities are J/g, kJ/kg, and BTU/lb-mass. The SI unit of Heat Capacity is J/g
- Molar Heat Capacity:
- Molar Heat Capacity is similar to Specific Heat Capacity. It expresses the amount of Heat required to raise one gram-mole of a substance by one degree Celsius
- It is expressed in J/mol-°C. The Molar Heat Capacity of water is 75.37 J/mol-°C
Mathematical Model
There are a few ways to find the Specific Heat Capacity of a material or system, such as the Thermal Energy equation, the Law of Dulong and Petit, or the Einstein-Debye Model.
Thermal Energy Equation
The relationship between the Heat and Temperature change of a system is best defined by the Specific Heat constant [math]\displaystyle{ C }[/math] in the equation below:
- [math]\displaystyle{ \Delta Q = mC \Delta T }[/math]
For a review of the meaning of this equation, view Thermal Energy Equation.
It is important to note this equation does not apply if a phase change occurs (say from a liquid state to a gaseous state).
Rearranging this equation gives us a way to calculate the Specific Heat Capacity of the system:
- [math]\displaystyle{ C = \frac{\Delta Q}{m \Delta T} = \frac{1}{m}\frac{dQ}{dT} }[/math]
We can in fact see a dependence on the Temperature of the system here. We can rewrite this as:
- [math]\displaystyle{ Q = m \int_{T_1}^{T_2} C \ dT }[/math]
If we know the dependence of the Specific Heat Capacity on Temperature, we can solve for the change in Thermal Energy.
Law of Dulong and Petit
The Law of Dulong and Petit is a Thermodynamic law discovered in 1819 by the French physicists Pierre Louis Dulong and Alexis Thérèse Petit. It yields the expression for the Molar Specific Heat Capacity of certain chemical elements. They found, through experiments, that the Mass Specific Heat Capacity for many elements was close to a constant value, after it had been adjusted to reflect the relative atomic weight of the element.
Basically, Dulong and Petit found that the Specific Heat Capacity of a mole of numerous solid elements is about 3R, where R is the universal gas constant. Dulong and Petit were unaware of the relationship to R, since it had not yet been defined. The value of 3R is about [math]\displaystyle{ 25 \ \frac{J}{mol \cdot K} }[/math], and Dulong and Petit found that this was the approximate Molar Specific Heat Capacity of some solid elements per mole of atoms they contained.
- For example, The Specific Heat Capacity of copper is [math]\displaystyle{ 0.385 \ \frac{J}{g \cdot K} }[/math]. The Specific Heat Capacity of lead is [math]\displaystyle{ 0.128 \ \frac{J}{g \cdot K} }[/math]. Why are the values so different in these two metals? Did you notice that they are expressed as energy per unit mass? If you express each as energy per mole, they are actually very similar. The Law of Dulong and Petit addresses this similarity in molar specific heats. It can be accounted for by applying equipartition of energy to the atoms of solids:
- [math]\displaystyle{ \text{Energy per mole} = 3kTN_{A} }[/math], where
- [math]\displaystyle{ k = }[/math] Boltzmann's constant
- [math]\displaystyle{ T = }[/math] Temperature in Kelvin
- [math]\displaystyle{ N_{A} = }[/math] Avogadro's Number
- [math]\displaystyle{ k = }[/math] Boltzmann's constant
- [math]\displaystyle{ \text{Energy per mole} = 3kTN_{A} }[/math], where
- [math]\displaystyle{ \text{The Law of Dulong and Petit:} \quad C = \frac{\partial}{\partial T}\left(3kTN_{a} \right) = \frac{3kN_{a}}{mol} = 24.94 \ \frac{J}{mol \cdot K} }[/math]
- To see the Molar Specific Heat Capacity, we multiply the Mass Specific Heat Capacity by the mass per mole of the substance. This molar basis, the Molar Specific Heat Capacity of copper and lead, are as follows:
- [math]\displaystyle{ \text{Copper:} \ C_{c} \times \left(\frac{M}{mol}\right)_{c} = 0.385 \times 63.546 = 24.5 \ \frac{J}{mol \cdot K} }[/math]
- [math]\displaystyle{ \text{Lead:} \ C_{l} \times \left(\frac{M}{mol}\right)_{l} = 0.128 \times 207.2 = 26.5 \ \frac{J}{mol \cdot K} }[/math]
- Here are a few more examples:
- [math]\displaystyle{ \text{Aluminum:} \ 24.3 \ \frac{J}{mol \cdot K} }[/math]
- [math]\displaystyle{ \text{Gold:} \ 25.6 \ \frac{J}{mol \cdot K} }[/math]
- [math]\displaystyle{ \text{Silver:} \ 24.9 \ \frac{J}{mol \cdot K} }[/math]
- [math]\displaystyle{ \text{Zinc:} \ 25.2 \ \frac{J}{mol \cdot K} }[/math]
Einstein-Debye Model
Einstein and Debye each developed a model for Specific Heat Capacity separately. Einstein's model stated that low energy excitation of a solid material was caused by the oscillation of a single atom, whereas Debye's model stated that phonons or collective modes iterating through a material caused excitations. However, these two models are able to be put together to find the Specific Heat Capacity given by the following formula:
- [math]\displaystyle{ C_{metal} = C_{electron} + C_{phonon} = \frac{{\pi}^2 N {k_{B}}^2}{2E_{f}}T + \frac{12{\pi}^4 N k_{b}}{5{T_{D}}^3}T^3 }[/math]
For low temperatures, Einstein and Debye found that the Law of Dulong and Petit was not applicable. At lower temperatures, it was found that atomic interactions were deemed significant in calculating the Molar Specific Heat Capacity of an object:
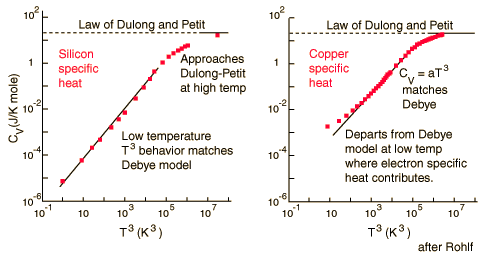
According to the Einstein Debye Model for Copper and Aluminum, specific heat varies a lot at lower temperatures and goes much below the Dulong-Petit Model. This is due to increased effects on specific heat by interatomic forces. However, for very high temperatures, the Einstein-Debye Model cannot be used. In fact, at high temperatures, Einstein's expression of specific heat reduces to the Dulong-Petit mathematical expression.
The Einstein Debye Equation is below:
- [math]\displaystyle{ C = \frac{\partial E}{\partial T} = \frac{3N_{A}k_{B}\left(\frac{hv}{k_{B}T}\right)^2 e^{hv/k_{B}T}}{\left(e^{hv/k_{B}T} - 1 \right)^2} \ mole^{-1} }[/math]
For high temperatures it may be reduced like this:
- [math]\displaystyle{ C \approx \frac{3N_{A}k_{B}\left(\frac{hv}{k_{B}T}\right)^2 \left(1 + \frac{hv}{k_{B}T} \right)}{\left(\frac{hv}{k_{B}T} \right)^2} \ mole^{-1} }[/math]
- [math]\displaystyle{ C \approx 3N_{A}k_{B}\left(1 + \frac{hv}{k_{B}T} \right) mole^{-1} \approx 3N_{A}k_{B} \ mole^{-1} }[/math]
Computational Model
- Insert Model Here
Examples
To the right is a table containing the Specific Heat Capacity for a variety of atoms that will be useful for the examples.

Simple
350 grams of an unknown substance is heated from 22ºC to 173ºC with 34,700 Joules of energy. There is no phase change.
- a) What is the Specific Heat Capacity ([math]\displaystyle{ C }[/math]) of this unknown substance?
- Applying the main equation of our Mathematical Model solves this in one step"
- [math]\displaystyle{ C = \frac{\Delta Q}{m \Delta T} }[/math]
- We know the value of everything in this equation except [math]\displaystyle{ C }[/math]:
- [math]\displaystyle{ C = \frac{34,700}{350 \times (173 - 22)} = 0.66 \ \frac{J}{gºC} }[/math]
- b) What is the Heat Capacity ([math]\displaystyle{ H }[/math]) of this unknown substance?
- To find the Heat Capacity of a sample of a substance, we must multiply the Specific Heat Capacity of the substance by the mass of the sample:
- [math]\displaystyle{ H = mC = 350 \times 0.66 = 231 \ \frac{J}{ºC} }[/math]
Middling
1,200 grams of coffee is sitting on a table is at a Temperature of [math]\displaystyle{ T_{co_{0}} = 93ºC }[/math]. Assume the Specific Heat Capacity of coffee is [math]\displaystyle{ 4.12 \ \frac{J}{gºC} }[/math]. The coffee is mixed with 55.3 grams of cream at [math]\displaystyle{ T_{cr_{0}} = 5ºC }[/math]. The Specific Heat Capacity of creamer is [math]\displaystyle{ 3.8 \ \frac{J}{gºC} }[/math].
- a) What is the final temperature of the mixture ([math]\displaystyle{ T_f }[/math]) , assuming that no Thermal Energy is lost to the surroundings, after the system reaches Thermal Equilibrium?
- Since no energy is lost to the surroundings, we can manipulate the energy principle as follows:
- [math]\displaystyle{ \Delta E_{system} + \Delta E_{surroundings} = 0 }[/math]
- [math]\displaystyle{ E_{system_{f}} - E_{system_{0}} = 0 }[/math]
- [math]\displaystyle{ E_{system_{f}} = E_{system_{0}} }[/math]
- [math]\displaystyle{ E_{co_{f}} + E_{cr_{f}} = E_{co_{0}} + E_{cr_{0}} }[/math] (1)
- We see that the final energy of the system must be equal to the initial energy of the system, the system being the coffee and the creamer mixture. All we know is that a Temperature change will occur in each part of the system. This change in Thermal Energy is proportional to the change in Temperature by:
- [math]\displaystyle{ \Delta Q = mC \Delta T }[/math]
- or:
- [math]\displaystyle{ Q_{f} - Q_{0} = mCT_{f} - mCT_{0} }[/math]
- or:
- [math]\displaystyle{ Q_{f} = mCT_{f} \quad Q_{0} = mCT_{0} }[/math] (2)
- The change in energy of the system will be due to only this change in Temperature:
- [math]\displaystyle{ \Delta E_{system} = \Delta Q_{system} }[/math] (3)
- From 1, 2, and 3, we see:
- [math]\displaystyle{ E_{system_{f}} - E_{system_{0}} = Q_{system_{f}} - Q_{system_{0}} = 0 }[/math]
- [math]\displaystyle{ (E_{co_{f}} + E_{cr_{f}}) - (E_{co_{0}} + E_{cr_{0}}) = (Q_{co_{f}} + Q_{cr_{f}}) - (Q_{co_{0}} + Q_{cr_{0}}) = 0 }[/math]
- [math]\displaystyle{ (Q_{co_{f}} + Q_{cr_{f}}) - (Q_{co_{0}} + Q_{cr_{0}}) = (m_{co}C_{co}T_{co_{f}} + m_{cr}C_{cr}T_{cr_{f}}) - (m_{co}C_{co}T_{co_{0}} + m_{cr}C_{cr}T_{cr_{0}}) = 0 }[/math] (4)
- Note, [math]\displaystyle{ T_{co_{f}} = T_{f} = T_{cr_{f}} }[/math], since the system is allowed to reach Thermal Equilibrium, reducing 4 to:
- [math]\displaystyle{ (m_{co}C_{co}T_{f} + m_{cr}C_{cr}T_{f}) - (m_{co}C_{co}T_{co_{0}} + m_{cr}C_{cr}T_{cr_{0}}) = 0 }[/math]
- [math]\displaystyle{ (m_{co}C_{co} + m_{cr}C_{cr})T_{f} - (m_{co}C_{co}T_{co_{0}} + m_{cr}C_{cr}T_{cr_{0}}) = 0 }[/math]
- [math]\displaystyle{ T_{f} = \frac{m_{co}C_{co}T_{co_{0}} + m_{cr}C_{cr}T_{cr_{0}}}{m_{co}C_{co} + m_{cr}C_{cr}} }[/math]
- Plugging in values gives:
- [math]\displaystyle{ T_{f} = \frac{(1,200 \times 4.12 \times 93) + (55.3 \times 3.8 \times 5)}{(1,200 \times 4.12) + (55.3 \times 3.8)} = 89.41ºC }[/math]
Difficult
At low temperatures, the Specific Heat Capacities of solids are typically proportional to [math]\displaystyle{ T^3 }[/math]. The first understanding of this behavior was due to the Dutch physicist Peter Debye, who in 1912, treated atomic oscillations with the quantum theory that Max Planck had recently used for radiation. For instance, a good approximation for the Specific Heat Capacity of salt, NaCl, is [math]\displaystyle{ C = 3.33 \times 10^4 \ \frac{J}{kg \cdot K}\left(\frac{T}{321K}\right)^3 }[/math]. The constant [math]\displaystyle{ 321 K }[/math] is called the Debye temperature of NaCl, [math]\displaystyle{ \theta_D }[/math], and the formula works well when [math]\displaystyle{ T \lt 0.04\theta_D }[/math].
- a) Using this formula, how much Heat is required to raise the Temperature of 24.0 g of NaCl from [math]\displaystyle{ 5 K \ \text{to} \ 15 K }[/math] ?
- We see there is a dependence on Temperature in our Specific Heat Capacity. Hence, we should use the last equation in our Thermal Energy Equation Section:
- [math]\displaystyle{ Q = m \int_{T_1}^{T_2} C \ dT }[/math]
- In this instance, the following quantities are defined for us:
- [math]\displaystyle{ m = 24g }[/math]
- [math]\displaystyle{ T_1 = 5K }[/math]
- [math]\displaystyle{ T_2 = 15K }[/math]
- [math]\displaystyle{ C = 3.33 \times 10^4 \ \frac{J}{kg \cdot K}\left(\frac{T}{321K} \right)^3 }[/math]
- We have all the info we need, so let's go ahead and solve:
- [math]\displaystyle{ Q = 0.024 \int_{5}^{15} 3.33 \times 10^4 \times \left(\frac{T}{321} \right)^3 \ dT }[/math]
- [math]\displaystyle{ Q = \frac{0.024 \times 3.33 \times 10^4}{321^3 \times 4}\left[T^4\right]_{5}^{15} }[/math]
- [math]\displaystyle{ Q = \left(6.04 \times 10^{-4} \ \frac{J}{K^4}\right)\left(15^4 - 5^4 \right) }[/math]
- [math]\displaystyle{ Q = 30.2 \ J }[/math]
Connectedness
The Specific Heat Capacity most commonly known is the Specific Heat Capacity of water, which is about 4.12 J/g°C or 1 calorie/g°C. The specific heat of water is higher than any other common substance. Water has a very large specific heat on a per-gram basis, meaning that it takes a lot more added heat to cause a change in its temperature. Since the specific heat of water is so high, water can be used for temperature regulation. Due to the difference in atomic structures, the specific heat per gram of water is much higher than that of a metal substance. It is possible to predict the specific heat of any material, as long as you know about its atomic structure, as a rise in temperature is the increase in energy at the atomic level of substances. Generally, it is more more useful to compare molar specific heats of substances.
It is easy to notice that water's specific heat capacity is much larger than anything else, but why? The answer is due to water's intermolecular forces. Since a water molecule is made up of one oxygen atom(negative charge) and two hydrogen atoms(slight positive charges), water has hydrogen bonds which result in the "sticking" of water molecules. Because of these hydrogen bonds, it requires a lot of energy to heat up water molecules, because not only do you have to use energy to increase the movement of the particle, but also to break the hydrogen bonds. As a result water has a high specific heat capacity because it takes a lot of energy to break the hydrogen bonds.
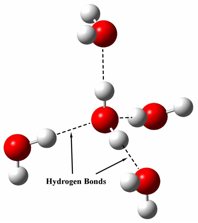
This is not an exclusive trait to water, however. The stronger the intermolecular forces of an object, generally the higher the specific heat capacity. Traditionally, gases and liquids have a higher specific heat capacity than solids. In addition, specific heat capacity is also related to the amount of kinetic energy possible in a molecule. Therefore, molecules with more available movement(liquids and gases), there is more room for the heat to "go". Because it is related to kinetic energy, as the external temperature approaches absolute zero, so does specific heat capacity.
But why is this important?
A large body of water can absorb and store a huge amount of heat from the sun in the daytime, such as during summer, while only warming up a few degrees. During night and Winter, the gradually cooling water can warm the air. This is the reason coastal areas generally have milder climates than inland rtegions. The high specific heat of water also tends to stabilize ocean temperatures, creating a favorable environment for marine life. Thus because of its high specific heat, the water that covers most of Earth keeps temperature fluctuations on land and in water within limits that permit life. Also, because organisms are primarily made of water, they are more able to resist changes in their own temperature than if they were made of a liquid with a lower specific heat.
Specific heat and Thermodynamics are used often in chemistry, nuclear engineering, aerodynamics, and mechanical engineering. It is also used in everyday life in the radiator and cooling system of a car.
Specific heat can have a lot to do with prosthetic manufacturing, which is a focus in Biomedical Engineering. Prosthetics materials must be durable and easy to manipulate in a normal range of temperatures. In order to created medical devices, specific heats must be known, especially for welding or molding things, which require a specific temperature to be effective. At higher temperatures, the Dulong-Petit law must be used to calculate the specific heat of an object. Especially for solid metal objects, which would be used in prosthetics, Dulong-Petit is very useful.
Cooking materials such as pots and pans are made to have a low specific heat so that they need less heat to raise their temperature. This allows for faster cooking processes. The handles of these cooking utensils are made of substances with high specific heats so that their temperature won’t rise too much if a large amount of heat is absorbed.
Have you ever noticed that sand on the beach can burn your feet but the ocean water is cool and refreshing? Sand has a lower specific heat than ocean water. So when the sun is beating down, the temperature of the land increases faster than that of the sea.
Insulation is made of materials with high specific heat so that they won't change temperature easily. For example, wood has a high specific heat. A wooden house helps keep the inside cooler during summer because it requires lots of heat to change its temperature. Builders can choose certain materials which allows us to build houses for specific locations and altitudes.
History

Dr. Joseph Black, of the University of Glasgow, was first credited with developing the concept of latent heat and Specific Heat Capacity in the mid 18th century. This allowed the study of Thermodynamics to be further looked in to. Before Specific Heat Capacity was known, scientists referred to Heat as some sort of invisible liquid. Black, while studying super-cooled water, noticed that when shaken, it instantly turned into ice. This lead him to the concept of "stored Heat," in that shaking it released some form of Heat. This was further developed into the idea that different substances responded to Heat changes differently. He performed an experiment by placing ice and super-cooled water in a room, and the water rapidly rose in temperature while the ice did not. This implied that more Heat was required to raise the Temperature of water than of ice. Black claimed, "If the complete change of ice and snow into water required only the further addition of a very small quantity of heat, the mass, though of considerable size, ought all to be melted in a few minutes or seconds more. Were this really the case, the consequences would be dreadful." After the establishment of the idea of Specific Heat Capacity and latent heat, scientists began to think of Heat as a system's change in internal energy. This is very important as the concept of Specific Heat Capacity has helped lead to the vast development of the field of Thermodynamics.
See also
Further reading
- Kinds of Matter
- Boiling Point
- Melting Point
- Thermal Energy
- First Law of Thermodynamics
- Second Law of Thermodynamics and Entropy
- Internal Energy
- Temperature
- Change of State
- Entropy and Enthalpy Calculations
- Elementary Principles of Chemical Processes (3rd Edition) By: Richard M. Felder & Ronald M. Rousseau
- Encyclopædia Britannica, 2015, "Heat capacity"
- Biology, 7th Edition by Neil A. Campbell and Jane B. Reece
External links
- WiseGeek.org
- KhanAcademy.org
- Wikipedia: Heat Capacity
- HyperPhysics Specific Heat
- Wikipedia: Heat Equation
- Specific Heat Simulation
References
- OpenStax Vol 2 Heat Transfer, Specific Heat, and Calorimetry
- HyperPhysics Concepts
- HyperPhysics Specific Heat
- Eric Weisstein's World of Physics: Specific Heat
- WIkiHow: How to Calculate Specific Heat
- KhanAcademy.org
- Applications of Specific Heat
- Uses of Specific Heat
- Law of Dulong and Petit
- Heat Capacity, Specific Heat, and Enthalpy
- Table of Specific Heats
- Heat Capacity and Water
- Joseph Black and Latent Heat
- Introduction to Chemical Engineering Thermodynamics Seventh Edition. J. M. Smith, H. C. Van Ness, Michael M. Abbott
- Matter & Interactions Vol I. Chabay Sherwood