Work Done By A Nonconstant Force: Difference between revisions

From Physics Book
Jump to navigation Jump to search
No edit summary
 
(72 intermediate revisions by 4 users not shown)
Line 1: Line 1:
'''Claimed by Yunqing Jia (Spring 2017)'''
Claimed by Amanda Barber Spring 2018
 
This page explains work done by non-constant forces. In addition, it provides  three levels of difficulty worked examples and analytical models will help readers develop a more thorough understanding.
 
Let's get started by first understanding what work is! Below is a fun cartoon explaining work!
[https://www.youtube.com/watch?v=bNuMhnhN2-A Work Cartoon]


This page explains the significance and fundamental calculations of work done by non-constant forces. In addition it provides multiple worked examples and analytical models will help readers develop a more thorough understanding.


==The Main Idea==
==The Main Idea==


[https://www.youtube.com/watch?v=RJgf4kvov9g]
Before you can understand work done by a nonconstant force, you have to understand work done by a constant force.
[[https://www.youtube.com/watch?v=RJgf4kvov9g]]
 
Work done by constant force of magnitude 'F' on a point that moves a displacement 'd' in the directional of the force is the product: W=F*d. The SI unit for work is the joule (J) which is equivalent to newton meter. Force is a relationship of the product of mass*acceleration of the object, while displace is a result of the change in final and starting position. It is important to note thatno matter how large or small the magnitude of the force is, no work is done if there is no displacement. The formula W=F*d only holds true when constant force is applied to the system.
For a better understanding of what a force is reference this video: [[https://www.youtube.com/watch?v=tC1tNIKztOo What is Force?]]
 
 
'''Work done by a Constant Force'''
 
[[File:ConstantForce.png|300 px]]
 
 
Work done by a constant force is dependent on the amount of newtons executed on the object and the distance traveled by the object. Above is an image depicting the formula W = F*d, where F is the force and d (or X) is the distance travelled. The formula W=F*d only holds true when a constant force is applied to the system.
 
While this formula is useful, it is not realistic to assume force will be constant in every system.
 
 
'''Work done by a Nonconstant Force'''
 
Work done by a nonconstant force is more commonly seen in every day life than work done by a constant force. You can tell if a force is nonconstant if the object moves a distance with a changing force at points along the path. Two examples of nonconstant forces are spring forces and gravitational forces. You can tell that gravitational force is a nonconstant force by observing the Moon's orbit and comparing different points on its path. If you choose points at different distances from the Earth to calculate the gravitational force on the Moon, you would observe that the gravitational force is greater at a closer distance from the Earth. Another example of a nonconstant force is a spring. If a spring had a constant force, the spring would forever stretch or compress rather than oscillate.
 
To calculate a nonconstant force you must use a different formula than W=F*d. An integral is needed to calculate the work done along a path of nonconstant force, where work is the is change in energy of a system by a force.
 
[[File:WorkIntegral.png|250px]]
 
 
===Mathematical Model===
 
 
[[File:particle.jpg|thumb|Particle with nonconstant force]]
 
The total amount of work done on a system is equal to the sum of the work done by all individual forces, therefore, the total amount of work done can be calculated by the summation of each force multiplied by the distance.
[[Iterative Prediction of Spring-Mass System|Iterative calculations]] are used in order to calculate non-constant forces and predict an object's motion. Given initial and final states of a system under non-constant force, small displacement intervals should be used to calculate the object's trajectory.
 
Below is the formula used to calculate each iteration then add them together to calculate total work.  


[[Iterative Prediction of Spring-Mass System|Iterative calculations]] are used in order to calculate non-constant forces and predict an object's motion. Given initial and final states of a system under non-constant force, small displacement intervals should be used to calculate the object's trajectory. As mentioned in [[Work|previous sections]], the total amount of work done on a system equals the sum of works done by all individual forces, therefore, the total amount of work done at a specific instance can be calculated by summing all previous ones.
<math>{{W}_{total} = {W}_{1} + {W}_{2} + {W}_{3} + ... + {W}_{n} = \overrightarrow{F}_{1}\bullet\overrightarrow{dr}_{1} + \overrightarrow{F}_{2}\bullet\overrightarrow{dr}_{2} + \overrightarrow{F}_{3}\bullet\overrightarrow{dr}_{3} + ... + \overrightarrow{F}_{n}\bullet\overrightarrow{dr}_{n}}</math>
<math>{{W}_{total} = {W}_{1} + {W}_{2} + {W}_{3} + ... + {W}_{n} = \overrightarrow{F}_{1}\bullet\overrightarrow{dr}_{1} + \overrightarrow{F}_{2}\bullet\overrightarrow{dr}_{2} + \overrightarrow{F}_{3}\bullet\overrightarrow{dr}_{3} + ... + \overrightarrow{F}_{n}\bullet\overrightarrow{dr}_{n}}</math>


wiki format reference:: <math>{{&Delta;p}_{system}} = {\vec{F}_{net}{&Delta;t}}</math>  
<math>{{W}_{total} = \sum\overrightarrow{F}\bullet\Delta\overrightarrow{r}}</math>


Common systems that deal with non-constant force are with springs and gravity. This is due to the change in spring force and gravitational force respectively. The work done on the system is found by integrating, or finding the area under the curve of force by displacement, we can calculate work without having to use inaccurate approximations.
This method, while possible, can get tedious and repetitive. If you make the intervals you calculate indefinitely small, it is the same as integrating. The most common formula used for work with a nonconstant force is the integral from the first point of a path to the last point.  


===A Mathematical Model===
<math>{{W}_{total} = \int\limits_{i}^{f}\overrightarrow{F}\bullet\overrightarrow{dr}}</math>


<math> W=\int\limits_{i}^{f}\overrightarrow{F}\bullet\overrightarrow{dr} = \sum\overrightarrow{F}\bullet\Delta\overrightarrow{r} </math>
Here is a graphical example of the integral.


This means that the work is equal to the integral of the function of the force with respect to the change in the objects position. This is also the same as the summation of the force on an object multiplied by the change in position.
[[File:Graphes.png|300 px]]


===A Computational Model===
===Computational Model===


<https://trinket.io/glowscript/49f7c0f35f>
[[File:Spring-Mass Motion along an axis.jpg|thumb|Spring-Mass Motion along an axis|250 px]]
[<https://trinket.io/glowscript/49f7c0f35f> Model of an Oscilating Spring]


This model shows both the total work and the work done by a spring on a ball attached to a vertical spring. The work done by the spring oscillates because the work is negative when the ball is moving away from the resting state and is positive when the ball moves towards it.
This model shows both the total work and the work done by a spring on a ball attached to a vertical spring. The work done by the spring oscillates because the work is negative when the ball is moving away from the resting state and is positive when the ball moves towards it.
Line 31: Line 65:


The code works by using small time steps of 0.01 seconds and finding the work done in each time step. Work is the summation of all of the work done in each time step, so another step makes sure the value for work is cumulative.
The code works by using small time steps of 0.01 seconds and finding the work done in each time step. Work is the summation of all of the work done in each time step, so another step makes sure the value for work is cumulative.
'''Modeling Non-Constant Forces in VPython'''
[[File:Spring-Mass Motion in a 2-D plane.jpg|thumb|Spring-Mass Motion in a 2-D plane|250 px]]
As shown in this trinket model, [https://trinket.io/glowscript/c26c4c2637 Planer Motion of a Spring-Mass System], computational models can also be used in predicting non-constant forces in multiple directions.
#intialize conditions
#calculation loop
  #calculate/update force at every time step
    L = ball.pos - spring.pos
    Lhat = norm(L)
    s = mag(L) - L0
    Fspring = -(ks * s) * Lhat
  #apply momentum principle
    ball.p = ball.p + (Fspring + Fgravity) * deltat
  #update positions
  #update time


==Examples==
==Examples==


===Example 1===
===Simple===
A box is pushed to the East, 5 meters by a force of 40 N, then it is pushed to the north 7 meters by a force of 60 N. Calculate the work done on the box.
 
'''Question'''
A box is pushed to the East 10 meters by a force of 40 N, then it is pushed to the north 8 meters by a force of 60 N.
Calculate the total work done on the box.
 
'''Solution'''


<math> W = \sum\overrightarrow{F}\bullet\Delta\overrightarrow{r} </math>
<math> W = \sum\overrightarrow{F}\bullet\Delta\overrightarrow{r} </math>


<math> W = 40N \bullet\ 5m + 60N \bullet\ 7m </math>
<math> W = 40N \bullet\ 10m + 60N \bullet\ 8m </math>


<math> W = 40N \bullet\ 5m + 60N \bullet\ 7m </math>
<math> W = 40N \bullet\ 10m + 60N \bullet\ 8m </math>


<math> W = 620 J </math>
<math> W = 880 J </math>


===Example 2===
===Middling===
We know that the formula for force is <math> F=ks </math>, where <math> s </math> is the distance the spring is stretched. If we integrate this with respect to <math> s </math>, we find that <math> W=.5ks^2 </math> is the formula for work.
 
We know that the formula for force is <math> F=ks </math>, where <math> s </math> is the distance the spring is stretched.  
If we integrate this with respect to <math> s </math>, we find that <math> W=.5ks^2 </math> is the formula for work.


<math> W=\int\limits_{i}^{f}\overrightarrow{k}\bullet\overrightarrow{ds} = .5ks^2 </math>
<math> W=\int\limits_{i}^{f}\overrightarrow{k}\bullet\overrightarrow{ds} = .5ks^2 </math>


Say that we want to find the work done by a horizontal spring with spring constant k=100 N/m as it moves an object 15 cm. Using the formula W=.5ks2 that we derived from F=ks, we can calculate that the work done by the spring is 1.125 J.
'''Question'''
 
Say that we want to find the work done by a horizontal spring with spring constant k=70 N/m as it moves an object 10 cm.  
 
[[File:Middle1.JPG]]
 
 
'''Solution'''
 
Using the formula W=.5ks2 that we derived from F=ks, we can calculate that the work done by the spring is 0.35 J.
 
<math> W=\int\limits_{0}^{10}70\bullet\overrightarrow{ds}=.5ks^2=.5(70)(0.10^2)=0.35 J </math>
 
===Difficult===
 
'''Question'''
 
The earth does work on an asteroid approaching from an initial distance d.
How much work is done on the asteroid by gravity before it hits the earth’s surface?
 
[[File:Diff1.JPG|300 px]]


<math> W=\int\limits_{0}^{15}100\bullet\overrightarrow{ds}=.5ks^2=.5(100)(0.15^2)=1.125 J </math>


===Example 3===
'''Solution'''
The earth does work on an asteroid approaching from an initial distance r. How much work is done on the asteroid by gravity before it hits the earth’s surface?


First, we must recall the formula for gravitational force.
First, we must recall the formula for gravitational force.


Because <math> G </math>, <math> M </math>, and <math> m </math> are constants, we can remove them from the integral. We also know that the integral of <math> -1\over r^2 </math> is <math> 1\over r </math>. We then must calculate the integral of <math> –GMm\over r^2 </math> from the initial radius of the asteroid, <math> R </math>, to the radius of the earth, <math> r </math>.  
Because <math> G </math>, <math> M </math>, and <math> m </math> are constants, we can remove them from the integral. We also know that the integral of <math> -1\over r^2 </math> is <math> 1\over r </math>. We then must calculate the integral of <math> –GMm\over d^2 </math> from the initial radius of the asteroid, <math> R </math>, to the radius of the earth, <math> r </math>.  


<math> W=-GMm\bullet\int\limits_{R}^{r}{-1\over r^2}\bullet dr </math>
<math> W=-GMm\bullet\int\limits_{R}^{r}{-1\over d^2}\bullet dr </math>


<math> W=-GMm\bullet({1\over r}-{1\over R}) </math>
<math> W=-GMm\bullet({1\over r}-{1\over R}) </math>


Our answer will be positive because the force done by the earth on the asteroid and the direction of the asteroid's displacement are the same.
Our answer will be positive because the forces done by the earth on the asteroid and the direction of the asteroid's displacement are the same.


==Connectedness==
==Connectedness==
I am most interested in the types of physics problems that accurately model real world situations. Some forces, like gravity near the surface of the earth and some machine-applied forces, are constant. However, most forces in the real world are not.  
The sector of physics that interests me the most is when I can see what I am computing. This unit covers spring forces. I can understand how the force is not constant because I can see the spring oscillating and changing positions and the amount of force.  


Because of this, calculating work for non-constant forces is essential to mechanical engineering. For example, when calculating work done by an engine over a distance, the force applied by the engine can vary depending on factors such as user controls.
Work done by a nonconstant force is related to my major, Industrial Engineering, because my major focuses heavily on optimization. Understanding how nonconstant forces work will help with machines in the workplace to help optimize efficiency.


On an industrial level, the work needed to fill and empty tanks depends on the weight of the liquid, which varies as the tanks fill and empty. Energy conversion in hydroelectric dams depends on the work done by water against turbines, which depends on the flow of water. Windmills work in the same way.
On an industrial level, the work needed to fill empty tanks depends on the weight of the liquid, which varies as the tanks fill and empty. Energy conversion in hydroelectric dams depends on the work done by water against turbines, which depends on the flow of water. Windmills work in the same way.


==History==


==History==
Gaspard-Gustave de Coriolis, famous for discoveries such as the Coriolis effect, is credited with naming the term “work” to define force applied over a distance. Later physicists combined this concept with Newtonian calculus to find work for non-constant forces.


Gaspard-Gustave de Coriolis, famous for discoveries such as the Coriolis effect, is credited with naming the term “work” to define force applied over a distance. Later physicists combined this concept with Newtonian calculus to find work for non-constant forces.


== See also ==
== See also ==


'''Further Reading'''
===Further Reading===
[[Work]]
 
Book:
 
Matter and Interactions - 4e Chabay and Sherwood
 
 
Article:
 
[[http://physics.tutorvista.com/forces/non-contact-force.html Non Constant Force]]
 
 
[[Iterative Prediction of Spring-Mass System]]


'''External Links'''
===External Links===


https://www.youtube.com/watch?v=jTkknXVjBl4
[[https://www.youtube.com/watch?v=jTkknXVjBl4 Work done by Non Constant Force]]


https://www.youtube.com/watch?v=9Be81qfgBVc
[[https://www.youtube.com/watch?v=9Be81qfgBVc Work done by Constant Force]]


==References==
==References==
Line 94: Line 182:
[http://www.britannica.com/biography/Gustave-Gaspard-Coriolis]
[http://www.britannica.com/biography/Gustave-Gaspard-Coriolis]
[http://www.math.northwestern.edu]
[http://www.math.northwestern.edu]
[https://p3server.pa.msu.edu/coursewiki/doku.php?id=183_notes:work]


[[Category:Energy]]
[[Category:Energy]]


Created by Justin Vuong
Created by Justin Vuong
Edited by Chris Mickas
Edited by Chris Mickas
Edited by Yunqing Jia
Edited by Noemi Nath

Latest revision as of 18:23, 18 August 2019

Claimed by Amanda Barber Spring 2018

This page explains work done by non-constant forces. In addition, it provides three levels of difficulty worked examples and analytical models will help readers develop a more thorough understanding.

Let's get started by first understanding what work is! Below is a fun cartoon explaining work! Work Cartoon


The Main Idea

Before you can understand work done by a nonconstant force, you have to understand work done by a constant force.

For a better understanding of what a force is reference this video: [What is Force?]


Work done by a Constant Force


Work done by a constant force is dependent on the amount of newtons executed on the object and the distance traveled by the object. Above is an image depicting the formula W = F*d, where F is the force and d (or X) is the distance travelled. The formula W=F*d only holds true when a constant force is applied to the system.

While this formula is useful, it is not realistic to assume force will be constant in every system.


Work done by a Nonconstant Force

Work done by a nonconstant force is more commonly seen in every day life than work done by a constant force. You can tell if a force is nonconstant if the object moves a distance with a changing force at points along the path. Two examples of nonconstant forces are spring forces and gravitational forces. You can tell that gravitational force is a nonconstant force by observing the Moon's orbit and comparing different points on its path. If you choose points at different distances from the Earth to calculate the gravitational force on the Moon, you would observe that the gravitational force is greater at a closer distance from the Earth. Another example of a nonconstant force is a spring. If a spring had a constant force, the spring would forever stretch or compress rather than oscillate.

To calculate a nonconstant force you must use a different formula than W=F*d. An integral is needed to calculate the work done along a path of nonconstant force, where work is the is change in energy of a system by a force.


Mathematical Model

File:Particle.jpg
Particle with nonconstant force

The total amount of work done on a system is equal to the sum of the work done by all individual forces, therefore, the total amount of work done can be calculated by the summation of each force multiplied by the distance. Iterative calculations are used in order to calculate non-constant forces and predict an object's motion. Given initial and final states of a system under non-constant force, small displacement intervals should be used to calculate the object's trajectory.

Below is the formula used to calculate each iteration then add them together to calculate total work.

[math]\displaystyle{ {{W}_{total} = {W}_{1} + {W}_{2} + {W}_{3} + ... + {W}_{n} = \overrightarrow{F}_{1}\bullet\overrightarrow{dr}_{1} + \overrightarrow{F}_{2}\bullet\overrightarrow{dr}_{2} + \overrightarrow{F}_{3}\bullet\overrightarrow{dr}_{3} + ... + \overrightarrow{F}_{n}\bullet\overrightarrow{dr}_{n}} }[/math]

[math]\displaystyle{ {{W}_{total} = \sum\overrightarrow{F}\bullet\Delta\overrightarrow{r}} }[/math]

This method, while possible, can get tedious and repetitive. If you make the intervals you calculate indefinitely small, it is the same as integrating. The most common formula used for work with a nonconstant force is the integral from the first point of a path to the last point.

[math]\displaystyle{ {{W}_{total} = \int\limits_{i}^{f}\overrightarrow{F}\bullet\overrightarrow{dr}} }[/math]

Here is a graphical example of the integral.

Computational Model

Spring-Mass Motion along an axis

[<https://trinket.io/glowscript/49f7c0f35f> Model of an Oscilating Spring]

This model shows both the total work and the work done by a spring on a ball attached to a vertical spring. The work done by the spring oscillates because the work is negative when the ball is moving away from the resting state and is positive when the ball moves towards it.

Because gravity causes the ball’s minimum position to be further from the spring’s resting length than its maximum position could be, the work is more negative when the ball approaches its minimum height.

The code works by using small time steps of 0.01 seconds and finding the work done in each time step. Work is the summation of all of the work done in each time step, so another step makes sure the value for work is cumulative.


Modeling Non-Constant Forces in VPython

Spring-Mass Motion in a 2-D plane

As shown in this trinket model, Planer Motion of a Spring-Mass System, computational models can also be used in predicting non-constant forces in multiple directions. 

#intialize conditions
#calculation loop
  #calculate/update force at every time step
    L = ball.pos - spring.pos
    Lhat = norm(L)
    s = mag(L) - L0
    Fspring = -(ks * s) * Lhat
  #apply momentum principle
    ball.p = ball.p + (Fspring + Fgravity) * deltat
 #update positions
 #update time

Examples

Simple

Question 

A box is pushed to the East 10 meters by a force of 40 N, then it is pushed to the north 8 meters by a force of 60 N.
Calculate the total work done on the box.

Solution

[math]\displaystyle{ W = \sum\overrightarrow{F}\bullet\Delta\overrightarrow{r} }[/math]

[math]\displaystyle{ W = 40N \bullet\ 10m + 60N \bullet\ 8m }[/math]

[math]\displaystyle{ W = 40N \bullet\ 10m + 60N \bullet\ 8m }[/math]

[math]\displaystyle{ W = 880 J }[/math]

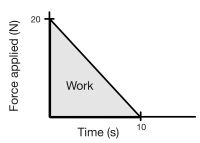
Middling

We know that the formula for force is [math]\displaystyle{ F=ks }[/math], where [math]\displaystyle{ s }[/math] is the distance the spring is stretched. If we integrate this with respect to [math]\displaystyle{ s }[/math], we find that [math]\displaystyle{ W=.5ks^2 }[/math] is the formula for work.

[math]\displaystyle{ W=\int\limits_{i}^{f}\overrightarrow{k}\bullet\overrightarrow{ds} = .5ks^2 }[/math]

Question

Say that we want to find the work done by a horizontal spring with spring constant k=70 N/m as it moves an object 10 cm.


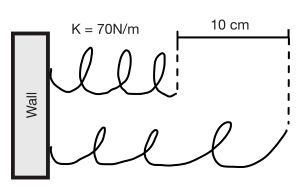
Solution

Using the formula W=.5ks2 that we derived from F=ks, we can calculate that the work done by the spring is 0.35 J.

[math]\displaystyle{ W=\int\limits_{0}^{10}70\bullet\overrightarrow{ds}=.5ks^2=.5(70)(0.10^2)=0.35 J }[/math]

Difficult

Question

The earth does work on an asteroid approaching from an initial distance d. How much work is done on the asteroid by gravity before it hits the earth’s surface?


Solution

First, we must recall the formula for gravitational force.

Because [math]\displaystyle{ G }[/math], [math]\displaystyle{ M }[/math], and [math]\displaystyle{ m }[/math] are constants, we can remove them from the integral. We also know that the integral of [math]\displaystyle{ -1\over r^2 }[/math] is [math]\displaystyle{ 1\over r }[/math]. We then must calculate the integral of [math]\displaystyle{ –GMm\over d^2 }[/math] from the initial radius of the asteroid, [math]\displaystyle{ R }[/math], to the radius of the earth, [math]\displaystyle{ r }[/math].

[math]\displaystyle{ W=-GMm\bullet\int\limits_{R}^{r}{-1\over d^2}\bullet dr }[/math]

[math]\displaystyle{ W=-GMm\bullet({1\over r}-{1\over R}) }[/math]

Our answer will be positive because the forces done by the earth on the asteroid and the direction of the asteroid's displacement are the same.

Connectedness

The sector of physics that interests me the most is when I can see what I am computing. This unit covers spring forces. I can understand how the force is not constant because I can see the spring oscillating and changing positions and the amount of force.

Work done by a nonconstant force is related to my major, Industrial Engineering, because my major focuses heavily on optimization. Understanding how nonconstant forces work will help with machines in the workplace to help optimize efficiency.

On an industrial level, the work needed to fill empty tanks depends on the weight of the liquid, which varies as the tanks fill and empty. Energy conversion in hydroelectric dams depends on the work done by water against turbines, which depends on the flow of water. Windmills work in the same way.

History

Gaspard-Gustave de Coriolis, famous for discoveries such as the Coriolis effect, is credited with naming the term “work” to define force applied over a distance. Later physicists combined this concept with Newtonian calculus to find work for non-constant forces.


See also

Further Reading

Book:

Matter and Interactions - 4e Chabay and Sherwood


Article:

[Non Constant Force]


Iterative Prediction of Spring-Mass System

External Links

[Work done by Non Constant Force]

[Work done by Constant Force]

References

[1] [2] [3]

Created by Justin Vuong

Edited by Chris Mickas

Edited by Yunqing Jia

Edited by Noemi Nath

Retrieved from "http://www.physicsbook.gatech.edu/index.php?title=Work_Done_By_A_Nonconstant_Force&oldid=37592"