Field of a Charged Rod: Difference between revisions
LukasYoder (talk | contribs) (Here is my Wiki Resource Submission) |
No edit summary |
||
| (62 intermediate revisions by 8 users not shown) | |||
| Line 1: | Line 1: | ||
'''Milo Karnes, Spring 2025''' | |||
''' | |||
== The Main Idea == | |||
In earlier studies, we learned about the electric field created by a point charge. However, in the real world, charges are often spread out over objects with shape and structure. One common example is a '''uniformly charged rod'''. To determine the electric field from such an object, we divide the rod into many infinitesimally small charge segments, treat each as a point charge, and integrate their contributions. | |||
The key idea is to approximate the rod as a continuous line of charge using the principle of superposition. We consider the symmetry of the setup to simplify the problem and focus on the components of the electric field that don't cancel out. | |||
The process of finding the electric field from a charged rod involves four main steps: | |||
# '''Model the rod as many small charge elements''' and draw the electric field vector <math>\Delta \vec{E}</math> from a single element. | |||
# '''Use symmetry''' to argue which components cancel and which remain. | |||
# '''Integrate''' the contributions from all elements to find the net electric field. | |||
# '''Verify''' that the result makes physical sense (units, direction, and limiting behavior). | |||
== A Mathematical Model == | |||
To calculate the electric field of a uniformly charged rod, we treat the rod as a continuous distribution of charge. Let the rod have total length <math>L</math> and total charge <math>Q</math>, centered along the x-axis. The observation point is located on the y-axis a distance <math>y</math> above the center. | |||
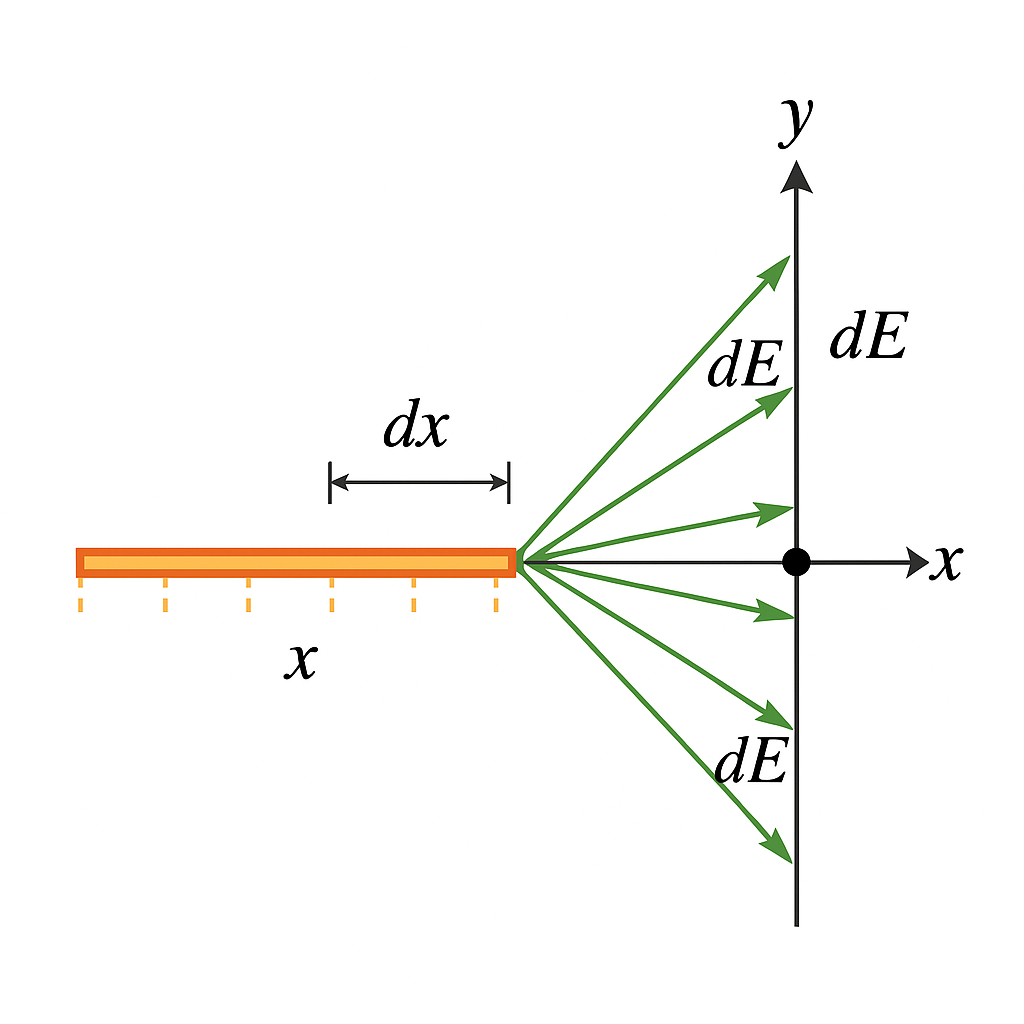
=== Step 1: Break the Rod into Pieces === | |||
We divide the rod into tiny segments of length <math>dx</math>. Each segment behaves like a point charge: | |||
<math> dq = \lambda \, dx </math>, where <math> \lambda = \frac{Q}{L} </math> is the linear charge density. | |||
Each <math>dq</math> contributes a small electric field <math> d\vec{E} </math> at the observation point. | |||
[[ | <div style="text-align: center;">[[File:ChargedRodBreakdown.png]]</div> | ||
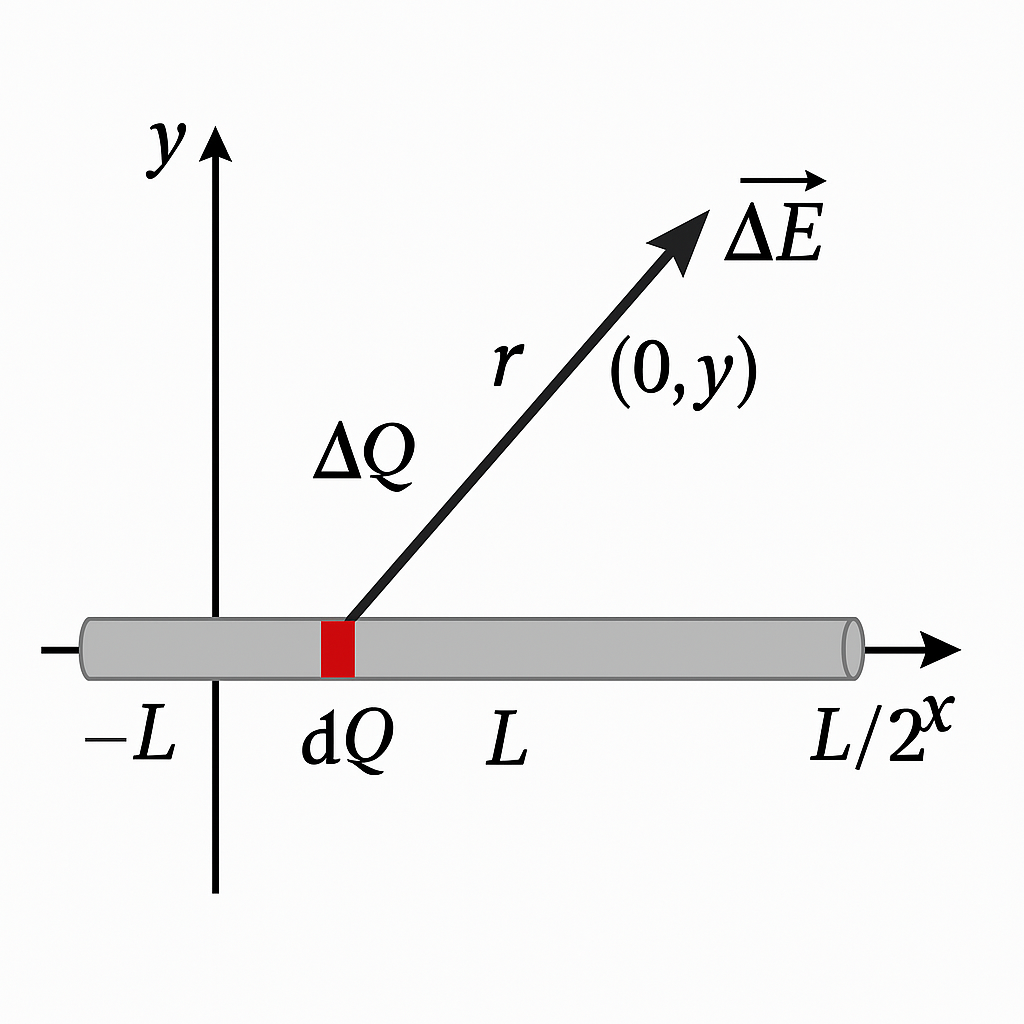
=== Step 2: Write the Field Expression for One Piece === | |||
Using Coulomb’s Law, the electric field contribution from one element is: | |||
= | <math> | ||
d\vec{E} = \frac{1}{4\pi\varepsilon_0} \cdot \frac{dq}{r^2} \cdot \hat{r} | |||
</math> | |||
The vector from the source to the observation point is: | |||
<math> \vec{r} = \langle 0, y \rangle - \langle x, 0 \rangle = \langle -x, y \rangle </math> | |||
So: | |||
<math> r = \sqrt{x^2 + y^2} \quad \text{and} \quad \hat{r} = \frac{\langle -x, y \rangle}{\sqrt{x^2 + y^2}} </math> | |||
Putting it all together: | |||
<math> | |||
d\vec{E} = \frac{1}{4\pi\varepsilon_0} \cdot \frac{\lambda \, dx}{(x^2 + y^2)} \cdot \frac{\langle -x, y \rangle}{\sqrt{x^2 + y^2}} | |||
= \frac{\lambda}{4\pi\varepsilon_0} \cdot \frac{\langle -x, y \rangle \, dx}{(x^2 + y^2)^{3/2}} | |||
</math> | |||
Note: The x-components of the field cancel due to symmetry. Only the y-component adds up. | |||
=== Step 3: Integrate === | |||
We | We now integrate from <math>-L/2</math> to <math>+L/2</math>: | ||
<math> | |||
E_y = \frac{\lambda y}{4\pi\varepsilon_0} \int_{-L/2}^{L/2} \frac{dx}{(x^2 + y^2)^{3/2}} | |||
</math> | |||
This integral has a standard solution: | |||
<math> | |||
E_y = \frac{\lambda}{4\pi\varepsilon_0 y} \cdot \left( \frac{L/2}{\sqrt{(L/2)^2 + y^2}} \right) | |||
</math> | |||
( | |||
Final result: | |||
<math> | |||
E_y = \frac{Q}{4\pi\varepsilon_0 L y} \cdot \left( \frac{L/2}{\sqrt{(L/2)^2 + y^2}} \right) | |||
</math> | |||
<div style="text-align: center;">[[File:ElectricFieldVectorFromRod.png]]</div> | |||
=== Step 4: Check the Result === | |||
* '''Units''': The result has units of N/C, as expected. | |||
* '''Direction''': The field points away from the rod if <math>Q > 0</math>, and toward the rod if <math>Q < 0</math>. | |||
* '''Limiting Behavior''': As <math>y \gg L</math>, the result simplifies to the electric field of a point charge: | |||
<math> | |||
E \approx \frac{Q}{4 \pi \varepsilon_0 y^2} | |||
</math> | |||
== Computational Models == | |||
While symbolic solutions give us a deep understanding of how to derive the electric field, computational models allow us to visualize it in action. This is especially useful when dealing with continuous charge distributions like a uniformly charged rod. | |||
GlowScript (a VPython-based simulation platform) makes it possible to numerically simulate and animate the electric field from a segmented rod. In these simulations, we treat the rod as a collection of small point charges, and compute the electric field vectors they produce at various locations in space. | |||
=== Field Mapping Along the Rod's Length === | |||
In this first simulation, the rod is broken into a series of green spheres, each representing a small segment of uniform charge. At various points near the rod, electric field vectors are plotted to show how the strength and direction of the field change along and around the rod. | |||
[http://www.glowscript.org/#/user/yoderlukas/folder/Public/program/ElectricFieldAlongRodLength '''▶ Run Simulation: Electric Field Along Rod'''] | |||
'''Key takeaways:''' | |||
* Observe how the direction of the field changes based on position. | |||
* Near the center of the rod, the field is strongest and most symmetric. | |||
* Near the ends, the field vectors curve — an effect known as ''edge effects''. | |||
* This illustrates why we often assume the rod is “infinitely long” in theory — to ignore those ends and simplify the math. | |||
This tool is particularly helpful for developing intuition before solving test problems involving rods, wires, or even capacitors. | |||
=== Radial Field Symmetry: Positive vs. Negative Charge === | |||
The next simulations demonstrate how the electric field behaves around a rod when it is positively or negatively charged. This is where direction matters — not just magnitude. | |||
* [https://www.glowscript.org/#/user/michaelwise/folder/Public/program/LineofCharge-Positive '''▶ Positive Rod Simulation'''] | |||
* [https://www.glowscript.org/#/user/michaelwise/folder/Public/program/LineofCharge-Negative '''▶ Negative Rod Simulation'''] | |||
These models break the rod into 40 discrete segments and compute the net electric field throughout a 2D grid surrounding the rod. | |||
'''Key observations:''' | |||
* Field lines from a positively charged rod '''point outward'''. | |||
* For a negatively charged rod, field lines '''point inward'''. | |||
* The symmetry is most noticeable when zoomed out — mimicking how an infinite line of charge behaves. | |||
* Near the ends, the distortion shows the importance of boundary conditions in real systems. | |||
These are powerful tools when preparing for conceptual questions or visual reasoning tasks — they help make the math real. | |||
=== Why It Matters === | |||
Computational models bridge the gap between the idealized math we do on paper and the messy, real-world systems we encounter in labs and engineering. They show us what electric fields actually look like when we account for discrete steps, edge effects, and variable observation points. | |||
They’re also interactive — you can zoom in, rotate, and change parameters. When studying for exams, use these models to test your intuition: If a question asks you about the direction of a field, imagine running one of these and predicting what it would look like. | |||
<small>All simulations above are written using GlowScript (VPython), and are free to edit or remix as part of your own projects or demonstrations.</small> | |||
== Examples == | |||
These examples cover different levels of conceptual and quantitative understanding of the electric field due to a uniformly charged rod. Try using the computational models above to visualize your answers! | |||
[http://www.glowscript.org/#/user/yoderlukas/folder/Public/program/ElectricFieldAlongRodLength | === Example 1: Symmetry and Direction (Conceptual) === | ||
You are observing a positively charged rod lying along the x-axis, centered at the origin. You stand at a point on the y-axis a distance <math>y</math> above the midpoint of the rod. | |||
'''Question:''' | |||
What direction does the electric field point at your location? | |||
'''Answer:''' | |||
The horizontal components of the field from symmetric charge elements cancel, and only the vertical (y-direction) components add constructively. Therefore, the electric field points directly upward (in the +y direction) if the rod is positively charged. | |||
=== Example 2: Deriving the Field at a Point (Symbolic) === | |||
A rod of total length <math>L = 2.0 \, \text{m}</math> carries a total charge <math>Q = 4.0 \times 10^{-6} \, \text{C}</math>. It lies along the x-axis, centered at the origin. Find the magnitude of the electric field at a point <math>y = 0.5 \, \text{m}</math> directly above its center. | |||
'''Solution:''' | |||
Use the derived formula: | |||
<math> | |||
E_y = \frac{Q}{4\pi\varepsilon_0 L y} \cdot \left( \frac{L/2}{\sqrt{(L/2)^2 + y^2}} \right) | |||
</math> | |||
Substitute known values: | |||
<math> | |||
\varepsilon_0 = 8.85 \times 10^{-12} \, \text{C}^2/\text{Nm}^2 | |||
</math> | |||
<math> | |||
E_y = \frac{4.0 \times 10^{-6}}{4\pi(8.85 \times 10^{-12}) \cdot (2.0)(0.5)} \cdot \left( \frac{1.0}{\sqrt{1.0^2 + 0.5^2}} \right) | |||
</math> | |||
Evaluate: | |||
<math> | |||
E_y \approx 2.3 \times 10^5 \, \text{N/C} | |||
</math> | |||
--- | |||
=== Example 3: Using the Simulation to Analyze Field Strength (Numerical/Visual) === | |||
Use the [Electric Field Along Rod Simulation](http://www.glowscript.org/#/user/yoderlukas/folder/Public/program/ElectricFieldAlongRodLength) to compare electric field strengths at two different points: | |||
* Point A: Directly above the midpoint of the rod | |||
* Point B: The same distance above one of the rod’s ends | |||
'''Question:''' | |||
Which point has a stronger electric field? How does the field direction differ? | |||
'''Reflection:''' | |||
The field at Point A is stronger and points vertically due to symmetry. At Point B, the field is weaker and points diagonally inward toward the rod’s center. This shows the importance of symmetry in superposition, and helps illustrate “edge effects” that are harder to account for with algebra alone. | |||
== Connectedness == | |||
At first glance, finding the electric field of a charged rod might just seem like a physics exercise, but it actually connects to a lot of real things — especially in aerospace. | |||
In spacecraft and satellites, components like power cables, structural booms, or tethers can hold charge and act basically like long rods. In space, charge builds up from sunlight or the plasma environment, and knowing how that charge creates electric fields helps engineers prevent issues like interference, arcing, or electrostatic discharge — which could damage sensitive electronics. | |||
Even in aircraft, stuff like static wicks or long sensor probes can behave like charged rods, and their fields matter for things like EMC (electromagnetic compatibility). We need to make sure systems don’t interfere with each other, especially in environments where you’ve got a bunch of tightly packed electrical components. | |||
As an AE major, I see this concept show up in ways I didn’t expect — whether it’s power systems on satellites, electrostatics in high-altitude flight, or how fields interact with composite materials. So yeah, we start with this simple charged rod, but the same physics applies all the way up to full-on orbital systems. | |||
== History == | |||
The idea that charged objects create electric fields has been around for a long time, but things really clicked in the 1700s when Charles-Augustin de Coulomb figured out how the force between charges actually worked. His experiments led to Coulomb’s Law, which became the foundation for electric field theory. | |||
Back then, most experiments focused on point charges because they were easier to understand and measure. But over time, physicists realized that most real objects — wires, rods, surfaces — aren’t point-like. That’s where the idea of continuous charge distributions came in. | |||
The charged rod is one of the first examples you see when learning how to deal with this. It helps build the foundation for understanding more complex things like rings, disks, and eventually 3D shapes. Once you learn how to break up a rod into tiny charge pieces and add up their fields, you can start doing the same for almost any shape. | |||
It’s kind of cool to think that this whole section — which starts with drawing a little rod and doing some integrals — is part of the same chain of ideas that eventually leads to things like electric field simulations for spacecraft or antennas. | |||
== See also == | |||
The equation for the electric field of a charged rod was derived from the equation for the electric field of a charged particle. See the article "[[Electric Field]]" for more information. | |||
=== Further Reading === | |||
The page on electric fields: [[Electric Field]] | |||
=== External Links === | |||
http://hyperphysics.phy-astr.gsu.edu/hbase/electric/elelin.html | |||
http://online.cctt.org/physicslab/content/phyapc/lessonnotes/Efields/EchargedRods.asp | |||
https://pages.uncc.edu/phys2102/online-lectures/chapter-02-electric-field/2-4-electric-field-of-charge-distributions/example-1-electric-field-of-a-charged-rod-along-its-axis/ | |||
http://dev.physicslab.org/Document.aspx?doctype=3&filename=Electrostatics_ContinuousChargedRod.xml | |||
== References == | |||
https://www.glowscript.org/#/ | |||
https://rhettallain_gmail_com.trinket.io/intro-to-electric-and-magnetic-fields#/electric-fields/multiple-charges | |||
https://www.youtube.com/watch?v=BBWd0zUe0mI | |||
(For the above reference, the textbook's method is followed in that the charge distribution was left undefined, and assumed to be constant) | |||
Chabay and Sherwood: Matter and Interactions, Fourth Edition, Chapter 15 | |||
[[Category: Electric Field]] | |||
Latest revision as of 16:05, 13 April 2025
Milo Karnes, Spring 2025
The Main Idea
In earlier studies, we learned about the electric field created by a point charge. However, in the real world, charges are often spread out over objects with shape and structure. One common example is a uniformly charged rod. To determine the electric field from such an object, we divide the rod into many infinitesimally small charge segments, treat each as a point charge, and integrate their contributions.
The key idea is to approximate the rod as a continuous line of charge using the principle of superposition. We consider the symmetry of the setup to simplify the problem and focus on the components of the electric field that don't cancel out.
The process of finding the electric field from a charged rod involves four main steps:
- Model the rod as many small charge elements and draw the electric field vector [math]\displaystyle{ \Delta \vec{E} }[/math] from a single element.
- Use symmetry to argue which components cancel and which remain.
- Integrate the contributions from all elements to find the net electric field.
- Verify that the result makes physical sense (units, direction, and limiting behavior).
A Mathematical Model
To calculate the electric field of a uniformly charged rod, we treat the rod as a continuous distribution of charge. Let the rod have total length [math]\displaystyle{ L }[/math] and total charge [math]\displaystyle{ Q }[/math], centered along the x-axis. The observation point is located on the y-axis a distance [math]\displaystyle{ y }[/math] above the center.
Step 1: Break the Rod into Pieces
We divide the rod into tiny segments of length [math]\displaystyle{ dx }[/math]. Each segment behaves like a point charge: [math]\displaystyle{ dq = \lambda \, dx }[/math], where [math]\displaystyle{ \lambda = \frac{Q}{L} }[/math] is the linear charge density.
Each [math]\displaystyle{ dq }[/math] contributes a small electric field [math]\displaystyle{ d\vec{E} }[/math] at the observation point.
Step 2: Write the Field Expression for One Piece
Using Coulomb’s Law, the electric field contribution from one element is:
[math]\displaystyle{ d\vec{E} = \frac{1}{4\pi\varepsilon_0} \cdot \frac{dq}{r^2} \cdot \hat{r} }[/math]
The vector from the source to the observation point is:
[math]\displaystyle{ \vec{r} = \langle 0, y \rangle - \langle x, 0 \rangle = \langle -x, y \rangle }[/math]
So:
[math]\displaystyle{ r = \sqrt{x^2 + y^2} \quad \text{and} \quad \hat{r} = \frac{\langle -x, y \rangle}{\sqrt{x^2 + y^2}} }[/math]
Putting it all together:
[math]\displaystyle{ d\vec{E} = \frac{1}{4\pi\varepsilon_0} \cdot \frac{\lambda \, dx}{(x^2 + y^2)} \cdot \frac{\langle -x, y \rangle}{\sqrt{x^2 + y^2}} = \frac{\lambda}{4\pi\varepsilon_0} \cdot \frac{\langle -x, y \rangle \, dx}{(x^2 + y^2)^{3/2}} }[/math]
Note: The x-components of the field cancel due to symmetry. Only the y-component adds up.
Step 3: Integrate
We now integrate from [math]\displaystyle{ -L/2 }[/math] to [math]\displaystyle{ +L/2 }[/math]:
[math]\displaystyle{ E_y = \frac{\lambda y}{4\pi\varepsilon_0} \int_{-L/2}^{L/2} \frac{dx}{(x^2 + y^2)^{3/2}} }[/math]
This integral has a standard solution:
[math]\displaystyle{ E_y = \frac{\lambda}{4\pi\varepsilon_0 y} \cdot \left( \frac{L/2}{\sqrt{(L/2)^2 + y^2}} \right) }[/math]
Final result:
[math]\displaystyle{ E_y = \frac{Q}{4\pi\varepsilon_0 L y} \cdot \left( \frac{L/2}{\sqrt{(L/2)^2 + y^2}} \right) }[/math]
Step 4: Check the Result
- Units: The result has units of N/C, as expected.
- Direction: The field points away from the rod if [math]\displaystyle{ Q \gt 0 }[/math], and toward the rod if [math]\displaystyle{ Q \lt 0 }[/math].
- Limiting Behavior: As [math]\displaystyle{ y \gg L }[/math], the result simplifies to the electric field of a point charge:
[math]\displaystyle{ E \approx \frac{Q}{4 \pi \varepsilon_0 y^2} }[/math]
Computational Models
While symbolic solutions give us a deep understanding of how to derive the electric field, computational models allow us to visualize it in action. This is especially useful when dealing with continuous charge distributions like a uniformly charged rod.
GlowScript (a VPython-based simulation platform) makes it possible to numerically simulate and animate the electric field from a segmented rod. In these simulations, we treat the rod as a collection of small point charges, and compute the electric field vectors they produce at various locations in space.
Field Mapping Along the Rod's Length
In this first simulation, the rod is broken into a series of green spheres, each representing a small segment of uniform charge. At various points near the rod, electric field vectors are plotted to show how the strength and direction of the field change along and around the rod.
▶ Run Simulation: Electric Field Along Rod
Key takeaways:
- Observe how the direction of the field changes based on position.
- Near the center of the rod, the field is strongest and most symmetric.
- Near the ends, the field vectors curve — an effect known as edge effects.
- This illustrates why we often assume the rod is “infinitely long” in theory — to ignore those ends and simplify the math.
This tool is particularly helpful for developing intuition before solving test problems involving rods, wires, or even capacitors.
Radial Field Symmetry: Positive vs. Negative Charge
The next simulations demonstrate how the electric field behaves around a rod when it is positively or negatively charged. This is where direction matters — not just magnitude.
These models break the rod into 40 discrete segments and compute the net electric field throughout a 2D grid surrounding the rod.
Key observations:
- Field lines from a positively charged rod point outward.
- For a negatively charged rod, field lines point inward.
- The symmetry is most noticeable when zoomed out — mimicking how an infinite line of charge behaves.
- Near the ends, the distortion shows the importance of boundary conditions in real systems.
These are powerful tools when preparing for conceptual questions or visual reasoning tasks — they help make the math real.
Why It Matters
Computational models bridge the gap between the idealized math we do on paper and the messy, real-world systems we encounter in labs and engineering. They show us what electric fields actually look like when we account for discrete steps, edge effects, and variable observation points.
They’re also interactive — you can zoom in, rotate, and change parameters. When studying for exams, use these models to test your intuition: If a question asks you about the direction of a field, imagine running one of these and predicting what it would look like.
All simulations above are written using GlowScript (VPython), and are free to edit or remix as part of your own projects or demonstrations.
Examples
These examples cover different levels of conceptual and quantitative understanding of the electric field due to a uniformly charged rod. Try using the computational models above to visualize your answers!
Example 1: Symmetry and Direction (Conceptual)
You are observing a positively charged rod lying along the x-axis, centered at the origin. You stand at a point on the y-axis a distance [math]\displaystyle{ y }[/math] above the midpoint of the rod.
Question: What direction does the electric field point at your location?
Answer: The horizontal components of the field from symmetric charge elements cancel, and only the vertical (y-direction) components add constructively. Therefore, the electric field points directly upward (in the +y direction) if the rod is positively charged.
Example 2: Deriving the Field at a Point (Symbolic)
A rod of total length [math]\displaystyle{ L = 2.0 \, \text{m} }[/math] carries a total charge [math]\displaystyle{ Q = 4.0 \times 10^{-6} \, \text{C} }[/math]. It lies along the x-axis, centered at the origin. Find the magnitude of the electric field at a point [math]\displaystyle{ y = 0.5 \, \text{m} }[/math] directly above its center.
Solution:
Use the derived formula:
[math]\displaystyle{ E_y = \frac{Q}{4\pi\varepsilon_0 L y} \cdot \left( \frac{L/2}{\sqrt{(L/2)^2 + y^2}} \right) }[/math]
Substitute known values:
[math]\displaystyle{ \varepsilon_0 = 8.85 \times 10^{-12} \, \text{C}^2/\text{Nm}^2 }[/math]
[math]\displaystyle{ E_y = \frac{4.0 \times 10^{-6}}{4\pi(8.85 \times 10^{-12}) \cdot (2.0)(0.5)} \cdot \left( \frac{1.0}{\sqrt{1.0^2 + 0.5^2}} \right) }[/math]
Evaluate:
[math]\displaystyle{ E_y \approx 2.3 \times 10^5 \, \text{N/C} }[/math]
---
Example 3: Using the Simulation to Analyze Field Strength (Numerical/Visual)
Use the [Electric Field Along Rod Simulation](http://www.glowscript.org/#/user/yoderlukas/folder/Public/program/ElectricFieldAlongRodLength) to compare electric field strengths at two different points:
- Point A: Directly above the midpoint of the rod
- Point B: The same distance above one of the rod’s ends
Question: Which point has a stronger electric field? How does the field direction differ?
Reflection: The field at Point A is stronger and points vertically due to symmetry. At Point B, the field is weaker and points diagonally inward toward the rod’s center. This shows the importance of symmetry in superposition, and helps illustrate “edge effects” that are harder to account for with algebra alone.
Connectedness
At first glance, finding the electric field of a charged rod might just seem like a physics exercise, but it actually connects to a lot of real things — especially in aerospace.
In spacecraft and satellites, components like power cables, structural booms, or tethers can hold charge and act basically like long rods. In space, charge builds up from sunlight or the plasma environment, and knowing how that charge creates electric fields helps engineers prevent issues like interference, arcing, or electrostatic discharge — which could damage sensitive electronics.
Even in aircraft, stuff like static wicks or long sensor probes can behave like charged rods, and their fields matter for things like EMC (electromagnetic compatibility). We need to make sure systems don’t interfere with each other, especially in environments where you’ve got a bunch of tightly packed electrical components.
As an AE major, I see this concept show up in ways I didn’t expect — whether it’s power systems on satellites, electrostatics in high-altitude flight, or how fields interact with composite materials. So yeah, we start with this simple charged rod, but the same physics applies all the way up to full-on orbital systems.
History
The idea that charged objects create electric fields has been around for a long time, but things really clicked in the 1700s when Charles-Augustin de Coulomb figured out how the force between charges actually worked. His experiments led to Coulomb’s Law, which became the foundation for electric field theory.
Back then, most experiments focused on point charges because they were easier to understand and measure. But over time, physicists realized that most real objects — wires, rods, surfaces — aren’t point-like. That’s where the idea of continuous charge distributions came in.
The charged rod is one of the first examples you see when learning how to deal with this. It helps build the foundation for understanding more complex things like rings, disks, and eventually 3D shapes. Once you learn how to break up a rod into tiny charge pieces and add up their fields, you can start doing the same for almost any shape.
It’s kind of cool to think that this whole section — which starts with drawing a little rod and doing some integrals — is part of the same chain of ideas that eventually leads to things like electric field simulations for spacecraft or antennas.
See also
The equation for the electric field of a charged rod was derived from the equation for the electric field of a charged particle. See the article "Electric Field" for more information.
Further Reading
The page on electric fields: Electric Field
External Links
http://hyperphysics.phy-astr.gsu.edu/hbase/electric/elelin.html
http://online.cctt.org/physicslab/content/phyapc/lessonnotes/Efields/EchargedRods.asp
http://dev.physicslab.org/Document.aspx?doctype=3&filename=Electrostatics_ContinuousChargedRod.xml
References
https://www.youtube.com/watch?v=BBWd0zUe0mI
(For the above reference, the textbook's method is followed in that the charge distribution was left undefined, and assumed to be constant)
Chabay and Sherwood: Matter and Interactions, Fourth Edition, Chapter 15