Simple Harmonic Motion: Difference between revisions
(→Simple) |
|||
| (46 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
'''Claimed for editing by Elton Leander Pinto 10/29/2018''' | '''Claimed for editing by Elton Leander Pinto 10/29/2018''' | ||
'''Edited by Richard Udall June 2019''' | |||
Simple harmonic motion is motion driven by a restorative force which acts to bring the oscillating particle back to its equilibrium position. Prototypical examples of this include a pendulum or a spring which is compressing and extending. However, most oscillating systems that we observe in our day-to-day life are not perfect simple harmonic oscillators. Simple harmonic motion is an approximation that ignores friction and air resistance. Although this is not generally true, simple harmonic motion is a decent approximation of these more complex systems. The more complex and accurate formulation which takes these forces into account is known as damped harmonic motion, and will be considered further in the page [[Iterative Prediction of Spring-Mass System]]. | |||
==The Main Idea== | ==The Main Idea== | ||
Simple harmonic motion is a periodic motion, a motion that is repeated over some time interval. This periodic motion has a restoring force, a force | Simple harmonic motion is a periodic motion, a motion that is repeated over some time interval. This periodic motion has a restoring force, which is a force which attempts to restore the system to its equilibrium position, and which is proportional and opposite in direction to displacement. Thus, the further the system is from its equilibrium position, the larger the force which acts to return it to equilibrium position. As the object gets closer to equilibrium position, the force decreases until is magnitude reaches zero. At the equilibrium, the particle has no forces acting upon it, but it now has a large amount of momentum, and so it passes the equilibrium point going in the opposite direction. As moves in the opposite direction from the equilibrium, the restoring forces increases in the opposite direction until the momentum reaches zero, after which the particle begins moving back towards the equilibrium. This process repeats, which leads to the periodic motion characteristic of the system. Common examples of simple harmonic motion include an undamped spring-mass system, and a pendulum swinging back and forth (in the idealized case where it does not slow down). | ||
[[File:Simple Harmonic Motion Orbit.gif|thumb|Simple Harmonic Motion Orbit]] | |||
===A Mathematical Model=== | ===A Mathematical Model=== | ||
We | Simple harmonic motion occurs very frequently in our treatment of physical systems, and is a useful approximation for many because it is often reasonably accurate, and because we have the tools to describe it exactly. We may consider the example of the spring (see the figure) to arrive at a general equation for simple harmonic motion, and tweak its parameters to obtain an equation that is well suited to describe the oscillatory motion of spring-mass systems. If we are to pull the mass a tad bit away from its equilibrium position and then let go, we see that the spring-mass system seems to undergo some kind of periodic motion. To find a mathematical representation for such a motion, we may draw an analogy between this behavior and the mathematics at our disposal. | ||
After a fixed period of time, we will find the system returns to its original state. Use of terminology such as period should remind one of precalculus, and specifically of the sinusoidal functions sine and cosine. Let us suppose then that the position can be described by a cosine function (we choose cosine instead of sine by convention, since in other methods of derivation it is more convenient to choose one over the other). We also know from observing the motion of the object that its position depends upon the frequency and amplitude of oscillations. Hopefully you remember how to parameterize a circle: we define <math> x = R\cos(t) </math> and <math> y = R \sin(t) </math>, where <math> R </math> is the radius, and we take <math> t </math> from 0 to <math> 2\pi </math>. However, we could just as easily assume that <math> t </math> keeps going past <math> 2\pi </math>, or that it takes on negative values, since it will stay on the circle; we just know that it will trace out a circle over a period of <math> 2\pi </math>. By this same token, we can also choose to give <math> t </math> a coefficient, writing the equations as <math> x = R\cos(2\pi t) </math> and <math> y = R\sin(2\pi t)</math>. Then the circle will be traced out as <math> t </math> goes from 0 to 1. If we were to make the coefficient <math> \pi </math> instead, then <math> t </math> would go from 0 to 2. Thus its period would be twice as large. All of this guides how we will now write out the equation for a spring. We know that the period will affect the argument inside the cosine, and the distance it travels will be determined by the coefficient outside. Calling the maximum distance the system will extend the amplitude, <math> A </math>, and calling the inverse of the period the frequency, <math> f </math>, we have the generic equation | |||
<math>x(t) = A \cos(2\pi f t)</math> | |||
By further convention, we'll rewrite this in terms of angular frequency <math> \omega = 2 \pi f </math>, giving | |||
<math> x(t) = A \cos(\omega t) </math> | |||
We | We may also generalize this to assume that it does not start at maximum extension, by introducing a phase factor <math> \phi </math> | ||
<math>x(t) = Acos(ωt + φ)</math> | |||
Now let us consider the prominent example of a Hookean spring. The force of an ideal spring-mass system can be found using <math>\vec{F}={-k}*\vec{s}</math> where <math>\vec{s}=\vec{L}-{\vec{L}_{o}}</math>. This equation stems from Newton's Second Law <ref>https://en.wikipedia.org/wiki/Newton%27s_laws_of_motion</ref> and Hooke's Law<ref>https://en.wikipedia.org/wiki/Hooke%27s_law</ref> which is a first order linear approximation for forces acting on an elastic system, such as a spring. The solution to this differential equation is <math>x=A\cos(\omega t + \phi)</math> where <math>ω=\sqrt{k/m}</math>. Combining this equation with our knowledge of sinusoidal functions, we define the period of oscillation to be <math>T=2π/ω</math>. | |||
[[Image:SimpleHarmonicOscillation.png|500px]] | |||
<div class="toccolours mw-collapsible mw-collapsed" style="width:700px; overflow:auto;"> | |||
<div style="font-weight:bold;line-height:1.6;">Advanced: Derivation with Differential Equations</div> | |||
<div class="mw-collapsible-content"> | |||
Our differential equation is given by Hooke's Law and Newton's Second Law: | |||
<math> x''(t) = -\frac{k}{m}x(t) </math> | |||
This is a very nice equation (it is linear with constant coefficients)<ref> http://www.feynmanlectures.caltech.edu/I_21.html </ref>, so we may solve it by creating a linear combination of two known solutions<ref> http://tutorial.math.lamar.edu/Classes/DE/ComplexRoots.aspx </ref>. As it happens, we know two functions that can solve this equation: <math>x_1(t) = a\cos(\omega t) </math> and <math> x_2 (t) = b\sin(\omega t)</math>, where <math> \omega^2 = k/m </math>, so that a double derivative gives <math> x_1''(t) = -a \omega^2 \cos(\omega t) = - \frac{k}{m} x_1(t) </math>, and etc. for <math> x_2 </math>. Then any solution may be written as | |||
<math> x(t) = a \cos(\omega t) + b\sin(\omega t) </math> | |||
Now, to make this a convenient form, lets call <math> A = \sqrt{a^2 + b^2} </math>, and pull it out, giving | |||
<math>x(t) = A cos( | <math> x(t) = A\biggr{(} \frac{a}{A} \cos(\omega t) + \frac{b}{A}\sin(\omega t) \biggr{)} </math> | ||
By construction, these fractions look a lot like the definition of cosine and sine from trigonometry, and so we call them these respectively. Now, we can use<ref> http://www.sosmath.com/trig/Trig5/trig5/trig5.html </ref> to reduce this to | |||
<math> x(t) = A \cos(\omega t + \phi) </math> | |||
Now, we want to determine the constants. If the initial velocity is zero, this is easy: <math> A = x_i </math> and <math> \phi = 0 </math>. Otherwise, we will need to use the initial value conditions: | |||
<math>x( | <math> x(0) = A \cos(\phi) </math> | ||
<math> x'(0) = A\omega \sin(\phi) </math> | |||
Taking a ratio of these two and solving for <math> \phi </math> will lead to | |||
<math> \phi = \arctan\biggr{(}\frac{x'(0)}{\omega x(0)}\biggr{)} </math> | |||
Finally, this may be substituted into either equation to solve for <math> A </math> | |||
</div></div> | |||
===A Computational Model=== | ===A Computational Model=== | ||
| Line 63: | Line 74: | ||
===Simple=== | ===Simple=== | ||
Problem: A spring has a restoring force of 300 N when it is | Problem: A spring has a restoring force of <math> 300 N </math> when it is compressed <math> 0.2 m </math>. What is the spring's constant <math>k</math> in <math>N/m</math>? | ||
<div class="toccolours mw-collapsible mw-collapsed" style="width:400px; overflow:auto;"> | <div class="toccolours mw-collapsible mw-collapsed" style="width:400px; overflow:auto;"> | ||
| Line 69: | Line 80: | ||
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
<math>F={- | Hooke's law gives | ||
<math>\vec{F}=-k\vec{s}</math> | |||
So rearranging gives | |||
<math>-k=\frac{\vec{F}}{\vec{s}}</math> | |||
<math>{ | Orienting the direction of extension as the positive direction, we have <math> \vec{F} = 300 N </math> and <math> \vec{s} = -0.2 m </math> | ||
<math> | <math>-k=\frac{300 N}{-.2 m}</math> | ||
<math>{ | <math>k=\frac{1500N}{m}</math> | ||
</div></div> | </div></div> | ||
| Line 85: | Line 102: | ||
<div style="font-weight:bold;line-height:1.6;">Solution</div> | <div style="font-weight:bold;line-height:1.6;">Solution</div> | ||
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
First, we have by definition that | |||
<math>T= | <math>T=\frac{2\pi}{\omega}</math> | ||
<math>T=8.88 | and using the formula for <math> \omega </math> gives | ||
<math>T=2\pi\sqrt{\frac{m}{k}}</math> | |||
<math>k=15 (N/m)</math> and <math>m=30kg</math> | |||
<math>T=2\pi \sqrt{\frac{30 kg}{15(N/m)}}</math> | |||
<math>T=8.88 s</math> | |||
</div></div> | </div></div> | ||
| Line 103: | Line 127: | ||
<div style="font-weight:bold;line-height:1.6;">Solution</div> | <div style="font-weight:bold;line-height:1.6;">Solution</div> | ||
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
<math>x= | <math>x=A\cos(\omega t)</math> | ||
<math>x | <math>\frac{x}{A}=\cos\biggr{(}\sqrt{\frac{k}{m}}t\biggr{)}</math> | ||
<math>1/2=cos( | <math>1/2=\cos\biggr{(}\sqrt{\frac{18 (N/m)}{2 kg}}t\biggr{)}</math> | ||
<math> | <math>\arccos(1/2)=3(Hz) \cdot t</math> | ||
<math>t=. | <math>t=.35 s</math> | ||
</div></div> | </div></div> | ||
==Connectedness== | ==Connectedness== | ||
[A student should expand upon this] | |||
One interesting application of simple harmonic motion is its ability to approximate the interatomic vibration of molecules which I find very interesting as an Earth and Atmospheric Science major, trying to better understand our environment and how the molecules it is made up of interact. I have always been very intrigued by the composition and interactions of molecules and this approximations brings me another step closer to understanding how our world works. An interesting industrial application of simple harmonic motion is its approximation of a car running on worn down shock absorbers. | One interesting application of simple harmonic motion is its ability to approximate the interatomic vibration of molecules which I find very interesting as an Earth and Atmospheric Science major, trying to better understand our environment and how the molecules it is made up of interact. I have always been very intrigued by the composition and interactions of molecules and this approximations brings me another step closer to understanding how our world works. An interesting industrial application of simple harmonic motion is its approximation of a car running on worn down shock absorbers. | ||
| Line 137: | Line 145: | ||
==History== | ==History== | ||
Thomas Hooke, an English scientist, | Thomas Hooke, an English scientist, discovered what is now known as Hooke's Law in 1660 while working on the springs of watches.<ref> https://www.britannica.com/science/Hookes-law </ref> A remarkable physicist, Hooke was also a pioneer in optics, astronomy, and fluid mechanics. He supported a theory of evolution nearly two hundred years before Darwin (although he did not know about the principle of natural selection), devised the inverse square law which Newton adapted, and accurately described air as individual particles separated by large distances.<ref> https://www.britannica.com/biography/Robert-Hooke </ref> Harmonic motion is thus named because of its connection to music: instruments vibrate, and in doing so produce the sounds we perceive as music.<ref> https://www.britannica.com/science/simple-harmonic-motion </ref> The Fourier series allows for the expression of ''any'' periodic function in terms of sinusoids, meaning that a huge variety of phenomena in physics may be decomposed into simple harmonic motion. Furthermore, for reasons discussed in reference 8, harmonic oscillators are a strong approximation of many systems near equilibrium. The corresponding quantum harmonic oscillator is similarly useful in quantum mechanics. <ref> https://phys.libretexts.org/Bookshelves/University_Physics/Book%3A_University_Physics_(OpenStax)/Map%3A_University_Physics_III_-_Optics_and_Modern_Physics_(OpenStax)/7%3A_Quantum_Mechanics/7.5%3A_The_Quantum_Harmonic_Oscillator </ref>. | ||
== See also == | == See also == | ||
*[[Fundamentals of Iterative Prediction with Varying Force]] | |||
[[ | *[[Iterative Prediction of Spring-Mass System]] | ||
*[[Two Dimensional Harmonic Motion]] | |||
===External links=== | ===External links=== | ||
https://www.khanacademy.org/science/physics/oscillatory-motion/harmonic-motion/v/introduction-to-harmonic-motion | *https://www.khanacademy.org/science/physics/oscillatory-motion/harmonic-motion/v/introduction-to-harmonic-motion | ||
*http://hyperphysics.phy-astr.gsu.edu/hbase/shm.html | |||
http://hyperphysics.phy-astr.gsu.edu/hbase/shm.html | *https://en.wikibooks.org/wiki/A-level_Physics_(Advancing_Physics)/Simple_Harmonic_Motion/Mathematical_Derivation | ||
*http://www.feynmanlectures.caltech.edu/I_21.html | |||
===Further Reading=== | |||
*Matter and Interactions, 4th Edition | |||
==References== | ==References== | ||
<references/> | <references/> | ||
Latest revision as of 15:24, 29 July 2019
Claimed for editing by Elton Leander Pinto 10/29/2018
Edited by Richard Udall June 2019
Simple harmonic motion is motion driven by a restorative force which acts to bring the oscillating particle back to its equilibrium position. Prototypical examples of this include a pendulum or a spring which is compressing and extending. However, most oscillating systems that we observe in our day-to-day life are not perfect simple harmonic oscillators. Simple harmonic motion is an approximation that ignores friction and air resistance. Although this is not generally true, simple harmonic motion is a decent approximation of these more complex systems. The more complex and accurate formulation which takes these forces into account is known as damped harmonic motion, and will be considered further in the page Iterative Prediction of Spring-Mass System.
The Main Idea
Simple harmonic motion is a periodic motion, a motion that is repeated over some time interval. This periodic motion has a restoring force, which is a force which attempts to restore the system to its equilibrium position, and which is proportional and opposite in direction to displacement. Thus, the further the system is from its equilibrium position, the larger the force which acts to return it to equilibrium position. As the object gets closer to equilibrium position, the force decreases until is magnitude reaches zero. At the equilibrium, the particle has no forces acting upon it, but it now has a large amount of momentum, and so it passes the equilibrium point going in the opposite direction. As moves in the opposite direction from the equilibrium, the restoring forces increases in the opposite direction until the momentum reaches zero, after which the particle begins moving back towards the equilibrium. This process repeats, which leads to the periodic motion characteristic of the system. Common examples of simple harmonic motion include an undamped spring-mass system, and a pendulum swinging back and forth (in the idealized case where it does not slow down).
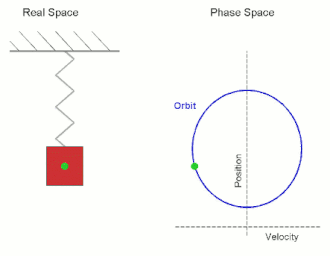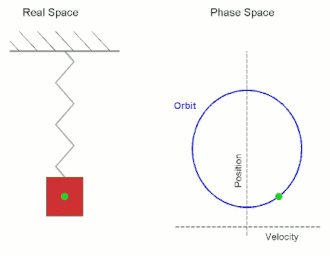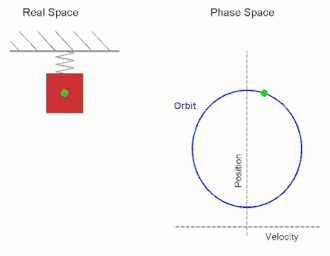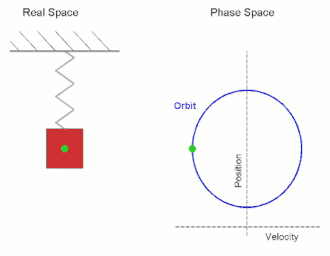
A Mathematical Model
Simple harmonic motion occurs very frequently in our treatment of physical systems, and is a useful approximation for many because it is often reasonably accurate, and because we have the tools to describe it exactly. We may consider the example of the spring (see the figure) to arrive at a general equation for simple harmonic motion, and tweak its parameters to obtain an equation that is well suited to describe the oscillatory motion of spring-mass systems. If we are to pull the mass a tad bit away from its equilibrium position and then let go, we see that the spring-mass system seems to undergo some kind of periodic motion. To find a mathematical representation for such a motion, we may draw an analogy between this behavior and the mathematics at our disposal. After a fixed period of time, we will find the system returns to its original state. Use of terminology such as period should remind one of precalculus, and specifically of the sinusoidal functions sine and cosine. Let us suppose then that the position can be described by a cosine function (we choose cosine instead of sine by convention, since in other methods of derivation it is more convenient to choose one over the other). We also know from observing the motion of the object that its position depends upon the frequency and amplitude of oscillations. Hopefully you remember how to parameterize a circle: we define [math]\displaystyle{ x = R\cos(t) }[/math] and [math]\displaystyle{ y = R \sin(t) }[/math], where [math]\displaystyle{ R }[/math] is the radius, and we take [math]\displaystyle{ t }[/math] from 0 to [math]\displaystyle{ 2\pi }[/math]. However, we could just as easily assume that [math]\displaystyle{ t }[/math] keeps going past [math]\displaystyle{ 2\pi }[/math], or that it takes on negative values, since it will stay on the circle; we just know that it will trace out a circle over a period of [math]\displaystyle{ 2\pi }[/math]. By this same token, we can also choose to give [math]\displaystyle{ t }[/math] a coefficient, writing the equations as [math]\displaystyle{ x = R\cos(2\pi t) }[/math] and [math]\displaystyle{ y = R\sin(2\pi t) }[/math]. Then the circle will be traced out as [math]\displaystyle{ t }[/math] goes from 0 to 1. If we were to make the coefficient [math]\displaystyle{ \pi }[/math] instead, then [math]\displaystyle{ t }[/math] would go from 0 to 2. Thus its period would be twice as large. All of this guides how we will now write out the equation for a spring. We know that the period will affect the argument inside the cosine, and the distance it travels will be determined by the coefficient outside. Calling the maximum distance the system will extend the amplitude, [math]\displaystyle{ A }[/math], and calling the inverse of the period the frequency, [math]\displaystyle{ f }[/math], we have the generic equation
[math]\displaystyle{ x(t) = A \cos(2\pi f t) }[/math]
By further convention, we'll rewrite this in terms of angular frequency [math]\displaystyle{ \omega = 2 \pi f }[/math], giving
[math]\displaystyle{ x(t) = A \cos(\omega t) }[/math]
We may also generalize this to assume that it does not start at maximum extension, by introducing a phase factor [math]\displaystyle{ \phi }[/math]
[math]\displaystyle{ x(t) = Acos(ωt + φ) }[/math]
Now let us consider the prominent example of a Hookean spring. The force of an ideal spring-mass system can be found using [math]\displaystyle{ \vec{F}={-k}*\vec{s} }[/math] where [math]\displaystyle{ \vec{s}=\vec{L}-{\vec{L}_{o}} }[/math]. This equation stems from Newton's Second Law [1] and Hooke's Law[2] which is a first order linear approximation for forces acting on an elastic system, such as a spring. The solution to this differential equation is [math]\displaystyle{ x=A\cos(\omega t + \phi) }[/math] where [math]\displaystyle{ ω=\sqrt{k/m} }[/math]. Combining this equation with our knowledge of sinusoidal functions, we define the period of oscillation to be [math]\displaystyle{ T=2π/ω }[/math].
Our differential equation is given by Hooke's Law and Newton's Second Law:
[math]\displaystyle{ x''(t) = -\frac{k}{m}x(t) }[/math]
This is a very nice equation (it is linear with constant coefficients)[3], so we may solve it by creating a linear combination of two known solutions[4]. As it happens, we know two functions that can solve this equation: [math]\displaystyle{ x_1(t) = a\cos(\omega t) }[/math] and [math]\displaystyle{ x_2 (t) = b\sin(\omega t) }[/math], where [math]\displaystyle{ \omega^2 = k/m }[/math], so that a double derivative gives [math]\displaystyle{ x_1''(t) = -a \omega^2 \cos(\omega t) = - \frac{k}{m} x_1(t) }[/math], and etc. for [math]\displaystyle{ x_2 }[/math]. Then any solution may be written as
[math]\displaystyle{ x(t) = a \cos(\omega t) + b\sin(\omega t) }[/math]
Now, to make this a convenient form, lets call [math]\displaystyle{ A = \sqrt{a^2 + b^2} }[/math], and pull it out, giving
[math]\displaystyle{ x(t) = A\biggr{(} \frac{a}{A} \cos(\omega t) + \frac{b}{A}\sin(\omega t) \biggr{)} }[/math]
By construction, these fractions look a lot like the definition of cosine and sine from trigonometry, and so we call them these respectively. Now, we can use[5] to reduce this to
[math]\displaystyle{ x(t) = A \cos(\omega t + \phi) }[/math]
Now, we want to determine the constants. If the initial velocity is zero, this is easy: [math]\displaystyle{ A = x_i }[/math] and [math]\displaystyle{ \phi = 0 }[/math]. Otherwise, we will need to use the initial value conditions:
[math]\displaystyle{ x(0) = A \cos(\phi) }[/math]
[math]\displaystyle{ x'(0) = A\omega \sin(\phi) }[/math]
Taking a ratio of these two and solving for [math]\displaystyle{ \phi }[/math] will lead to
[math]\displaystyle{ \phi = \arctan\biggr{(}\frac{x'(0)}{\omega x(0)}\biggr{)} }[/math]
Finally, this may be substituted into either equation to solve for [math]\displaystyle{ A }[/math]
A Computational Model
Simple harmonic motion in vPython uses glowscript to implement a varying force iterative motion predictor, while this has uses numpy to do the same (here the cell with simp_harm_func is the one we wish to look at). For a detailed description of how varying force computational methods work, see Fundamentals of Iterative Prediction with Varying Force. The important distinction of simple harmonic motion is that it is defined by the force function
[math]\displaystyle{ F(t,x,v) = -kx }[/math]
Where by convention we have [math]\displaystyle{ k \gt 0 }[/math].
Examples
Simple
Problem: A spring has a restoring force of [math]\displaystyle{ 300 N }[/math] when it is compressed [math]\displaystyle{ 0.2 m }[/math]. What is the spring's constant [math]\displaystyle{ k }[/math] in [math]\displaystyle{ N/m }[/math]?
Hooke's law gives
[math]\displaystyle{ \vec{F}=-k\vec{s} }[/math]
So rearranging gives
[math]\displaystyle{ -k=\frac{\vec{F}}{\vec{s}} }[/math]
Orienting the direction of extension as the positive direction, we have [math]\displaystyle{ \vec{F} = 300 N }[/math] and [math]\displaystyle{ \vec{s} = -0.2 m }[/math]
[math]\displaystyle{ -k=\frac{300 N}{-.2 m} }[/math]
[math]\displaystyle{ k=\frac{1500N}{m} }[/math]
Middling
Problem: What is the oscillation period of a spiring with spring constant 15N/m with a 30 kg mass attached?
First, we have by definition that
[math]\displaystyle{ T=\frac{2\pi}{\omega} }[/math]
and using the formula for [math]\displaystyle{ \omega }[/math] gives
[math]\displaystyle{ T=2\pi\sqrt{\frac{m}{k}} }[/math]
[math]\displaystyle{ k=15 (N/m) }[/math] and [math]\displaystyle{ m=30kg }[/math]
[math]\displaystyle{ T=2\pi \sqrt{\frac{30 kg}{15(N/m)}} }[/math]
[math]\displaystyle{ T=8.88 s }[/math]
Difficult
Problem: A spring with spring constant 18 N/m has mass of 2 kg is attached to it. The mass is then displaced to x = 2 . How much time does it take for the block to travel to the point x = 1?
Solution:
[math]\displaystyle{ x=A\cos(\omega t) }[/math]
[math]\displaystyle{ \frac{x}{A}=\cos\biggr{(}\sqrt{\frac{k}{m}}t\biggr{)} }[/math]
[math]\displaystyle{ 1/2=\cos\biggr{(}\sqrt{\frac{18 (N/m)}{2 kg}}t\biggr{)} }[/math]
[math]\displaystyle{ \arccos(1/2)=3(Hz) \cdot t }[/math]
[math]\displaystyle{ t=.35 s }[/math]
Connectedness
[A student should expand upon this]
One interesting application of simple harmonic motion is its ability to approximate the interatomic vibration of molecules which I find very interesting as an Earth and Atmospheric Science major, trying to better understand our environment and how the molecules it is made up of interact. I have always been very intrigued by the composition and interactions of molecules and this approximations brings me another step closer to understanding how our world works. An interesting industrial application of simple harmonic motion is its approximation of a car running on worn down shock absorbers.
History
Thomas Hooke, an English scientist, discovered what is now known as Hooke's Law in 1660 while working on the springs of watches.[6] A remarkable physicist, Hooke was also a pioneer in optics, astronomy, and fluid mechanics. He supported a theory of evolution nearly two hundred years before Darwin (although he did not know about the principle of natural selection), devised the inverse square law which Newton adapted, and accurately described air as individual particles separated by large distances.[7] Harmonic motion is thus named because of its connection to music: instruments vibrate, and in doing so produce the sounds we perceive as music.[8] The Fourier series allows for the expression of any periodic function in terms of sinusoids, meaning that a huge variety of phenomena in physics may be decomposed into simple harmonic motion. Furthermore, for reasons discussed in reference 8, harmonic oscillators are a strong approximation of many systems near equilibrium. The corresponding quantum harmonic oscillator is similarly useful in quantum mechanics. [9].
See also
- Fundamentals of Iterative Prediction with Varying Force
- Iterative Prediction of Spring-Mass System
- Two Dimensional Harmonic Motion
External links
- https://www.khanacademy.org/science/physics/oscillatory-motion/harmonic-motion/v/introduction-to-harmonic-motion
- http://hyperphysics.phy-astr.gsu.edu/hbase/shm.html
- https://en.wikibooks.org/wiki/A-level_Physics_(Advancing_Physics)/Simple_Harmonic_Motion/Mathematical_Derivation
- http://www.feynmanlectures.caltech.edu/I_21.html
Further Reading
- Matter and Interactions, 4th Edition
References
- ↑ https://en.wikipedia.org/wiki/Newton%27s_laws_of_motion
- ↑ https://en.wikipedia.org/wiki/Hooke%27s_law
- ↑ http://www.feynmanlectures.caltech.edu/I_21.html
- ↑ http://tutorial.math.lamar.edu/Classes/DE/ComplexRoots.aspx
- ↑ http://www.sosmath.com/trig/Trig5/trig5/trig5.html
- ↑ https://www.britannica.com/science/Hookes-law
- ↑ https://www.britannica.com/biography/Robert-Hooke
- ↑ https://www.britannica.com/science/simple-harmonic-motion
- ↑ https://phys.libretexts.org/Bookshelves/University_Physics/Book%3A_University_Physics_(OpenStax)/Map%3A_University_Physics_III_-_Optics_and_Modern_Physics_(OpenStax)/7%3A_Quantum_Mechanics/7.5%3A_The_Quantum_Harmonic_Oscillator
