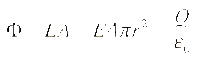Gauss's law: Difference between revisions
No edit summary |
No edit summary |
||
| (6 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
To be continued by Tony Chen wchen408 | To be continued by Tony Chen wchen408 | ||
===Topic Description=== | ===Topic Description=== | ||
Gauss's law is a method to determine the electric field for situations where the charges are contained in a closed surface. Gauss's law relates charges distribution with the concept of electric flux, which is essentially the amount of an electric field passing through a surface. <math>\Phi_E = \mathbf{E} \cdot \mathrm{d}\mathbf{A}\cos\Theta</math>. Gauss's law is always true, but for physics 2, it becomes only when calculating the electric field in situations with sufficient symmetry:[[File:Flux_Sphere.JPG|200px|thumb|right|Flux_Sphere]]] | Gauss's law is a method to determine the electric field for situations where the charges are contained in a closed surface. Gauss's law relates charges distribution with the concept of electric flux, which is essentially the amount of an electric field passing through a surface. <math>\Phi_E = \mathbf{E} \cdot \mathrm{d}\mathbf{A}\cos\Theta</math>. Gauss's law is always true, but for physics 2, it becomes only when calculating the electric field in situations with sufficient symmetry:[[File:Flux_Sphere.JPG|200px|thumb|right|Flux_Sphere]]] | ||
===Qualitative description=== | ===Qualitative description=== | ||
The electric flux that passes through a closed surface can be found by adding up all the charges enclosed by the closed surface divided by the constant ε0; or by adding up all the electric field on the gaussian surface dot dA(the infinitesimal surface area). As illustrate by the equation : <math>\Phi_E = \frac{Q}{\varepsilon_0}</math>, where Φ<sub>''E''</sub> is the electric flux through a closed surface ''S'' enclosing any volume ''V'', ''Q'' is the total electric charge enclosed within ''S'', and ''ε''<sub>0</sub> is the electric constant. T | The electric flux that passes through a closed surface can be found by adding up all the charges enclosed by the closed surface divided by the constant ε0; or by adding up all the electric field on the gaussian surface dot dA(the infinitesimal surface area). As illustrate by the equation : <math>\Phi_E = \frac{Q}{\varepsilon_0}</math>, where Φ<sub>''E''</sub> is the electric flux through a closed surface ''S'' enclosing any volume ''V'', ''Q'' is the total electric charge enclosed within ''S'', and ''ε''<sub>0</sub> is the electric constant. T | ||
===Integral Form=== | ===Integral Form=== | ||
When the surface is not uniform, we can calculate the electric flux by dividing the surface into infinite amount of small patches d'''A''', so all the each patch is essentially flat and the field is essentially uniform over each. Therefore, the flux of each patch is dΦ = ''E'' · ''d''A. The total flux is calculated by adding up the contribution of each patch, as illustrated by the equation below. | When the surface is not uniform, we can calculate the electric flux by dividing the surface into infinite amount of small patches d'''A''', so all the each patch is essentially flat and the field is essentially uniform over each. Therefore, the flux of each patch is dΦ = ''E'' · ''d''A. The total flux is calculated by adding up the contribution of each patch, as illustrated by the equation below. | ||
| Line 21: | Line 24: | ||
===Examples=== | ===Examples=== | ||
====Uniform Spherical Charge==== | ====Uniform Spherical Charge==== | ||
The electric field of a point charge Q can be obtained by a straightforward application of Gauss' law. Considering a Gaussian surface in the form of a sphere at radius r, the electric field has the same magnitude at every point of the sphere and is directed outward. The electric flux is then just the electric field times the area of the sphere. | The electric field of a point charge Q can be obtained by a straightforward application of Gauss' law. Considering a Gaussian surface in the form of a sphere at radius r, the electric field has the same magnitude at every point of the sphere and is directed outward. The electric flux is then just the electric field times the area of the sphere. | ||
[[File:sphere1.gif|200px|Sphere_Flux]] | |||
The electric field at radius r is then given by: | |||
[[File:sphere2.gif|120px|Sphere_Field]] | |||
== See also == | == See also == | ||
[[Ampere's Law]] | |||
[[Faraday's Law]] | |||
===Further reading=== | ===Further reading=== | ||
http://www.matterandinteractions.org | |||
http://www.colorado.edu/physics/phys1120/phys1120_sm13/lecture-notes/CH21.pdf | |||
==References== | ==References== | ||
| Line 45: | Line 49: | ||
http://www.ux1.eiu.edu/~addavis/1360/24Gauss/SphrChrg.html | http://www.ux1.eiu.edu/~addavis/1360/24Gauss/SphrChrg.html | ||
http://www4.ncsu.edu/~beichner/PY208/Docs/Software.htm | http://www4.ncsu.edu/~beichner/PY208/Docs/Software.htm | ||
https://en.wikipedia.org/wiki/Gauss%27s_law | |||
http://www.colorado.edu/physics/phys1120/phys1120_sm13/lecture-notes/CH21.pdf | |||
Latest revision as of 17:08, 29 November 2015
To be continued by Tony Chen wchen408
Topic Description
Gauss's law is a method to determine the electric field for situations where the charges are contained in a closed surface. Gauss's law relates charges distribution with the concept of electric flux, which is essentially the amount of an electric field passing through a surface. [math]\displaystyle{ \Phi_E = \mathbf{E} \cdot \mathrm{d}\mathbf{A}\cos\Theta }[/math]. Gauss's law is always true, but for physics 2, it becomes only when calculating the electric field in situations with sufficient symmetry:

]
Qualitative description
The electric flux that passes through a closed surface can be found by adding up all the charges enclosed by the closed surface divided by the constant ε0; or by adding up all the electric field on the gaussian surface dot dA(the infinitesimal surface area). As illustrate by the equation : [math]\displaystyle{ \Phi_E = \frac{Q}{\varepsilon_0} }[/math], where ΦE is the electric flux through a closed surface S enclosing any volume V, Q is the total electric charge enclosed within S, and ε0 is the electric constant. T
Integral Form
When the surface is not uniform, we can calculate the electric flux by dividing the surface into infinite amount of small patches dA, so all the each patch is essentially flat and the field is essentially uniform over each. Therefore, the flux of each patch is dΦ = E · dA. The total flux is calculated by adding up the contribution of each patch, as illustrated by the equation below.
where E is the electric field, dA is a vector representing an infinitesimal element of area, and · represents the dot product of two vectors.
Since the flux is defined as an integral of the electric field, this expression of Gauss's law is called the integral form.
A VPython Model
Visualizing Gauss's Law in Vpython Model, consider embedding some vpython code here Python Demo By Matter & Interactions 4e
Examples
Uniform Spherical Charge
The electric field of a point charge Q can be obtained by a straightforward application of Gauss' law. Considering a Gaussian surface in the form of a sphere at radius r, the electric field has the same magnitude at every point of the sphere and is directed outward. The electric flux is then just the electric field times the area of the sphere.
The electric field at radius r is then given by:
See also
Further reading
http://www.matterandinteractions.org http://www.colorado.edu/physics/phys1120/phys1120_sm13/lecture-notes/CH21.pdf
References
http://hyperphysics.phy-astr.gsu.edu/hbase/electric/elesph.html http://www.ux1.eiu.edu/~addavis/1360/24Gauss/SphrChrg.html http://www4.ncsu.edu/~beichner/PY208/Docs/Software.htm https://en.wikipedia.org/wiki/Gauss%27s_law http://www.colorado.edu/physics/phys1120/phys1120_sm13/lecture-notes/CH21.pdf