Field of a Charged Rod: Difference between revisions

From Physics Book
Jump to navigation Jump to search
No edit summary
 
(28 intermediate revisions by 5 users not shown)
Line 1: Line 1:
'''Milo Karnes, Spring 2025'''


== The Main Idea ==
In earlier studies, we learned about the electric field created by a point charge. However, in the real world, charges are often spread out over objects with shape and structure. One common example is a '''uniformly charged rod'''. To determine the electric field from such an object, we divide the rod into many infinitesimally small charge segments, treat each as a point charge, and integrate their contributions.
The key idea is to approximate the rod as a continuous line of charge using the principle of superposition. We consider the symmetry of the setup to simplify the problem and focus on the components of the electric field that don't cancel out.
The process of finding the electric field from a charged rod involves four main steps:
# '''Model the rod as many small charge elements''' and draw the electric field vector <math>\Delta \vec{E}</math> from a single element.
# '''Use symmetry''' to argue which components cancel and which remain.
# '''Integrate''' the contributions from all elements to find the net electric field.
# '''Verify''' that the result makes physical sense (units, direction, and limiting behavior).
== A Mathematical Model ==
To calculate the electric field of a uniformly charged rod, we treat the rod as a continuous distribution of charge. Let the rod have total length <math>L</math> and total charge <math>Q</math>, centered along the x-axis. The observation point is located on the y-axis a distance <math>y</math> above the center.
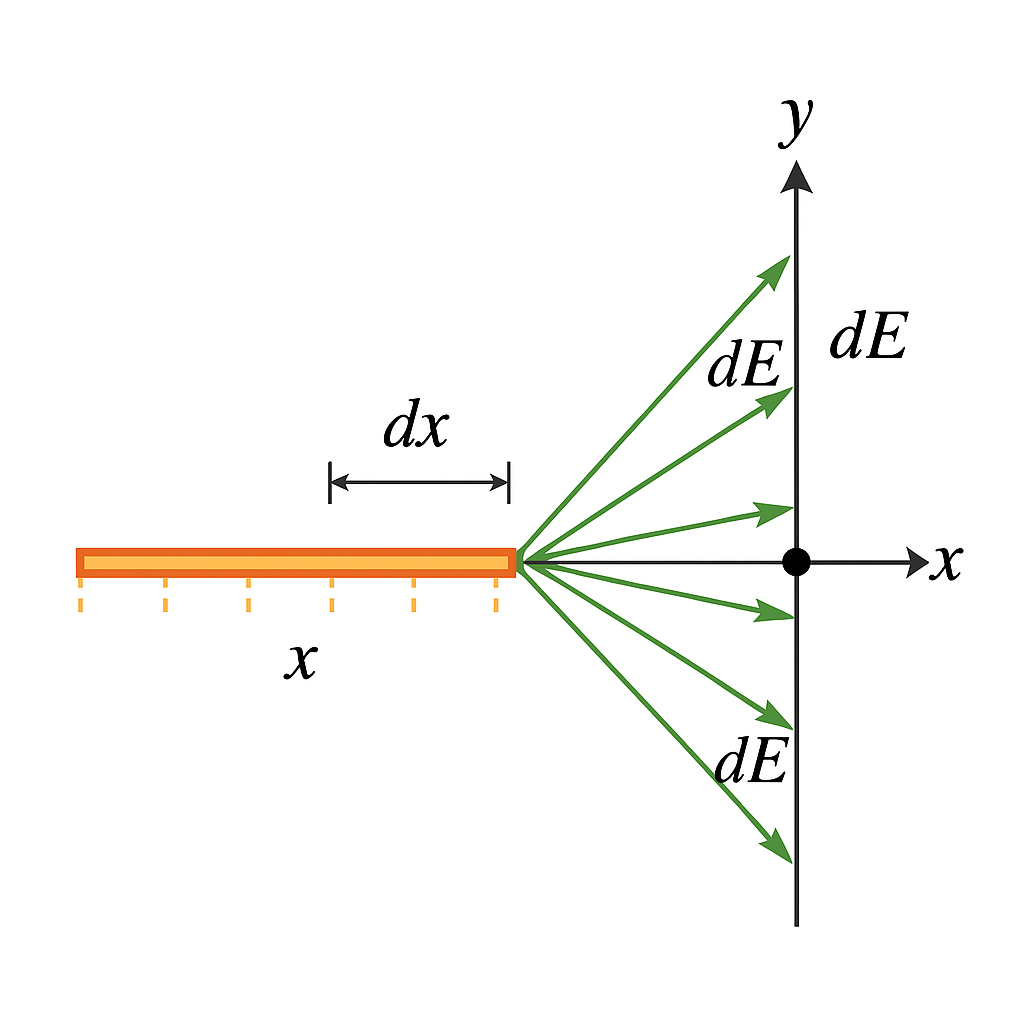
=== Step 1: Break the Rod into Pieces ===
We divide the rod into tiny segments of length <math>dx</math>. Each segment behaves like a point charge:
<math> dq = \lambda \, dx </math>, where <math> \lambda = \frac{Q}{L} </math> is the linear charge density.
Each <math>dq</math> contributes a small electric field <math> d\vec{E} </math> at the observation point.
<div style="text-align: center;">[[File:ChargedRodBreakdown.png]]</div>
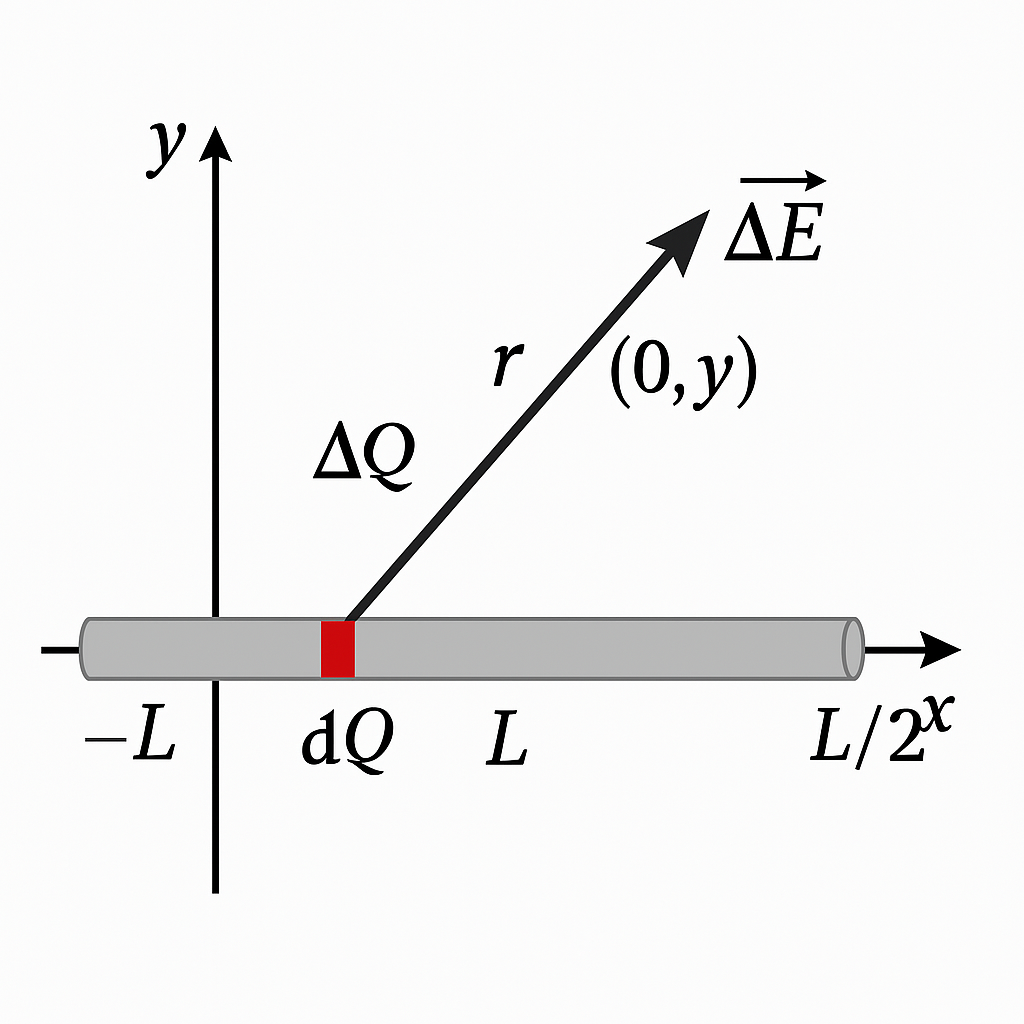
=== Step 2: Write the Field Expression for One Piece ===
Using Coulomb’s Law, the electric field contribution from one element is:
<math>
d\vec{E} = \frac{1}{4\pi\varepsilon_0} \cdot \frac{dq}{r^2} \cdot \hat{r}
</math>
The vector from the source to the observation point is:
<math> \vec{r} = \langle 0, y \rangle - \langle x, 0 \rangle = \langle -x, y \rangle </math>
So:
<math> r = \sqrt{x^2 + y^2} \quad \text{and} \quad \hat{r} = \frac{\langle -x, y \rangle}{\sqrt{x^2 + y^2}} </math>
Putting it all together:
<math>
d\vec{E} = \frac{1}{4\pi\varepsilon_0} \cdot \frac{\lambda \, dx}{(x^2 + y^2)} \cdot \frac{\langle -x, y \rangle}{\sqrt{x^2 + y^2}}
= \frac{\lambda}{4\pi\varepsilon_0} \cdot \frac{\langle -x, y \rangle \, dx}{(x^2 + y^2)^{3/2}}
</math>
Note: The x-components of the field cancel due to symmetry. Only the y-component adds up.
=== Step 3: Integrate ===
We now integrate from <math>-L/2</math> to <math>+L/2</math>:
<math>
E_y = \frac{\lambda y}{4\pi\varepsilon_0} \int_{-L/2}^{L/2} \frac{dx}{(x^2 + y^2)^{3/2}}
</math>
This integral has a standard solution:
<math>
E_y = \frac{\lambda}{4\pi\varepsilon_0 y} \cdot \left( \frac{L/2}{\sqrt{(L/2)^2 + y^2}} \right)
</math>
Final result:
<math>
E_y = \frac{Q}{4\pi\varepsilon_0 L y} \cdot \left( \frac{L/2}{\sqrt{(L/2)^2 + y^2}} \right)
</math>
<div style="text-align: center;">[[File:ElectricFieldVectorFromRod.png]]</div>
=== Step 4: Check the Result ===
* '''Units''': The result has units of N/C, as expected.
* '''Direction''': The field points away from the rod if <math>Q > 0</math>, and toward the rod if <math>Q < 0</math>.
* '''Limiting Behavior''': As <math>y \gg L</math>, the result simplifies to the electric field of a point charge:
<math>
E \approx \frac{Q}{4 \pi \varepsilon_0 y^2}
</math>
== Computational Models ==
While symbolic solutions give us a deep understanding of how to derive the electric field, computational models allow us to visualize it in action. This is especially useful when dealing with continuous charge distributions like a uniformly charged rod.
GlowScript (a VPython-based simulation platform) makes it possible to numerically simulate and animate the electric field from a segmented rod. In these simulations, we treat the rod as a collection of small point charges, and compute the electric field vectors they produce at various locations in space.
=== Field Mapping Along the Rod's Length ===
In this first simulation, the rod is broken into a series of green spheres, each representing a small segment of uniform charge. At various points near the rod, electric field vectors are plotted to show how the strength and direction of the field change along and around the rod.
[http://www.glowscript.org/#/user/yoderlukas/folder/Public/program/ElectricFieldAlongRodLength '''▶ Run Simulation: Electric Field Along Rod''']
'''Key takeaways:'''
* Observe how the direction of the field changes based on position.
* Near the center of the rod, the field is strongest and most symmetric.
* Near the ends, the field vectors curve — an effect known as ''edge effects''.
* This illustrates why we often assume the rod is “infinitely long” in theory — to ignore those ends and simplify the math.
This tool is particularly helpful for developing intuition before solving test problems involving rods, wires, or even capacitors.


== The Main Idea ==
=== Radial Field Symmetry: Positive vs. Negative Charge ===


Previously, we've learned about the electric field of a point particle. Often, when analyzing physical systems, it is the case that we're unable to analyze each individual particle that composes an object and need to therefore generalize collections of particles into shapes (in this case, a rod) whereby the mathematics corresponding to electric field calculations can be simplified. This can essentially be done by adding up the contributions to the electric field made by parts of an object, approximating each part of an object as a point charge.
The next simulations demonstrate how the electric field behaves around a rod when it is positively or negatively charged. This is where direction matters — not just magnitude.


Some objects, such as rods, can be modeled as a uniformly charged object in order to calculate the electric field at some observation location. The following wiki page provides an overview of electric fields created by uniformly charged thin rods, briefly presenting its inception, some specific cases, and proof of concept experiments. The case of a uniformly charged thin rod is a fundamental example of electric field patterns and calculations within physics. Its implications can be applied to other charged objects, such as rings, disks, and spheres.
* [https://www.glowscript.org/#/user/michaelwise/folder/Public/program/LineofCharge-Positive '''▶ Positive Rod Simulation''']
* [https://www.glowscript.org/#/user/michaelwise/folder/Public/program/LineofCharge-Negative '''▶ Negative Rod Simulation''']


In practical situations, objects have charges spread all over their surface. When going about calculating the electric fields of these objects, we can either use one of two processes: numerical summation or integration, or dividing an object into many pieces and summing the individual pieces' electric field contributions. As with point charges, the direction of the field is determined by the sign of the object's charge (positive-points away, negative-points toward) and the size of the field is determined by the observation distance and the magnitude of the object's charge.
These models break the rod into 40 discrete segments and compute the net electric field throughout a 2D grid surrounding the rod.


The process of finding the electric field due to charge distributed over an object has four steps:
'''Key observations:'''
* Field lines from a positively charged rod '''point outward'''.
* For a negatively charged rod, field lines '''point inward'''.
* The symmetry is most noticeable when zoomed out — mimicking how an infinite line of charge behaves.
* Near the ends, the distortion shows the importance of boundary conditions in real systems.


1. Divide the charged object into small pieces. Make a diagram and draw the electric field <math>\Delta \vec{E}</math> contributed by one of the pieces.
These are powerful tools when preparing for conceptual questions or visual reasoning tasks — they help make the math real.


2. Choose an origin and the axes. Write an algebraic expression for the electric field <math>\Delta \vec{E}</math> due to one piece.
=== Why It Matters ===


3. Add up the contributions of all pieces, either numerically or symbolically.
Computational models bridge the gap between the idealized math we do on paper and the messy, real-world systems we encounter in labs and engineering. They show us what electric fields actually look like when we account for discrete steps, edge effects, and variable observation points.


4. Check that the result is physically correct.
They’re also interactive — you can zoom in, rotate, and change parameters. When studying for exams, use these models to test your intuition: If a question asks you about the direction of a field, imagine running one of these and predicting what it would look like.


=== A Mathematical Model ===
<small>All simulations above are written using GlowScript (VPython), and are free to edit or remix as part of your own projects or demonstrations.</small>
The process of calculating a uniformly charged rod's electric field is tedious, but breaking the process down into several steps makes the task at hand easier. Consider a uniformly charged thin rod of length <math>L</math>  and positive charge <math>Q</math> centered on and lying along the x-axis. The rod is being observed from above at a point on the y-axis.


'''Step 1: Divide the Distribution into Pieces; Draw <math>\Delta \vec{E}</math>'''


Imagine dividing the rod into a series of very thin slices, each with the same charge <math>\Delta Q</math>. This charge <math>\Delta Q</math> is a small part of the overall charge.  Picture it as a point charge.  Each slice contributes its own electric field, <math>\Delta E</math>.  Summing all these individual slices of <math>E</math> gives you the total electric field of the rod.  This process is the same as taking an integral, as each thickness approaches 0 and the the number of slices approaches infinity.  Note that in this example, the variable that is changing for each slice is its x-coordinate.
== Examples ==


'''Step 2: Write an Expression for the Electric Field Due to One Piece'''
These examples cover different levels of conceptual and quantitative understanding of the electric field due to a uniformly charged rod. Try using the computational models above to visualize your answers!


The second step is to write a mathematical expression for the field <math>\Delta E</math> contributed by a single slice of the rod.  We use the formula of the electric field for a point charge because we are imagining each slice as a point charge.  First, determine <math>r</math>, the vector pointing from the source to the observation location.  For our example, this is <math> r = obs - source = <0,y,0> - < x,0,0> = <-x,y,0></math>.  Now use this to calculate the magnitude and direction of <math>r</math>.  So <math>|\vec{r}| = \sqrt{(-x)^2 + y^2} = \sqrt{x^2 + y^2}</math> and <math>\hat{r} = \frac{\vec{r}}{\hat{r}} = \frac{< -x,y,0>}{\sqrt{x^2 + y^2}} </math>. <math> \hat{r}</math> is the vector portion of the expression for the field.  The scalar portion is <math> \frac{1}{4\pi\epsilon_0} \cdot \frac{\Delta Q}{|\vec{r}|^2}</math>.  Thus the expression for one slice of the rod is:
=== Example 1: Symmetry and Direction (Conceptual) ===
<math> \Delta \vec{E} = \frac{1}{4\pi\epsilon_0} \cdot \frac{\Delta Q}{(\sqrt{x^2+y^2})^{3/2}} \cdot < -x,y,0> </math>.


'''Determining <math>\Delta Q</math> and the integration variable'''
You are observing a positively charged rod lying along the x-axis, centered at the origin. You stand at a point on the y-axis a distance <math>y</math> above the midpoint of the rod.


In the first step, we determined that the changing variable for this rod was its x-coordinate. This means the integration variable is <math> dx</math>.  We need to put this integration variable into our expression for the electric field. More specifically, we need to express <math>\Delta Q</math> in terms of the integration variable.  Recall that the rod is uniformly charged, so the charge on any single slice of it is: <math>
'''Question:'''  
\Delta Q = (\frac{\Delta x}{L})\cdot Q</math>.  This quantity can also be expressed in terms of the charge density.
What direction does the electric field point at your location?


'''Expression for <math> \Delta \vec{E}</math>
'''Answer:''' 
The horizontal components of the field from symmetric charge elements cancel, and only the vertical (y-direction) components add constructively. Therefore, the electric field points directly upward (in the +y direction) if the rod is positively charged.


Substitute the expression for the integration variable into the formula for the electric field of one slice. Separating the equation into separate x and y components, we get <math> \Delta \vec{E_x} = \frac{1}{4\pi\epsilon_0} \cdot \frac{Q}{L} \cdot \frac{-x}{(\sqrt{x^2+y^2})^{3/2}} \cdot dx  </math> and <math> \Delta \vec{E_y} = \frac{1}{4\pi\epsilon_0} \cdot \frac{Q}{L} \cdot \frac{y}{(\sqrt{x^2+y^2})^{3/2}} \cdot dx  </math>.  Note that we have replaced <math> \Delta x </math> with <math> dx</math> in preparation for integration.


'''Step 3: Add Up the Contributions of All the Pieces'''
=== Example 2: Deriving the Field at a Point (Symbolic) ===


The third step is to sum all of our slices.  We can go about this in two ways. One way is with numerical summation, or separating the object into a finite number of small pieces, calculating the individual contributing electric fields, and then summing them.  Another, more precise method is to integrate.  Most of the work of finding the field of a uniformly charged object is setting up this integral. If you have reached the correct expression to integrate, the rest is simple math.  The bounds for integration are the coordinates of the start and stop of the rod.  In this example the bounds are from <math>-L/2</math> to <math>+L/2</math>. So the expression is <math> \int\limits_{-L/2}^{L/2}\ \frac{1}{4\pi\epsilon_0} \cdot \frac{Q}{L} \cdot \frac{y}{(\sqrt{x^2+y^2})^{3/2}} \cdot dx. </math> Solving this gives the final expression <math> E_y = \frac{1}{4\pi\epsilon_0} \cdot \frac{Q}{x} \cdot \frac{1}{(\sqrt{x^2+ (L/2)^2})}    </math>. Note that the field parallel to the x axis is zero. This can be observed due to the symmetry of the problem.
A rod of total length <math>L = 2.0 \, \text{m}</math> carries a total charge <math>Q = 4.0 \times 10^{-6} \, \text{C}</math>. It lies along the x-axis, centered at the origin. Find the magnitude of the electric field at a point <math>y = 0.5 \, \text{m}</math> directly above its center.
This equation can be written more generally as <math> E = \frac{1}{4\pi\epsilon_0} \cdot \frac{Q}{r} \cdot \frac{1}{(\sqrt{r^2+ (L/2)^2})}    </math> where r represents the distance from the rod to the observation location.


'''Step 4:Checking the Result'''
'''Solution:'''


Finally, the fourth step is to check the result. The units should be the same as the units of the expression for the electric field for a single point particle <math> E = \frac{1}{4\pi\epsilon_0} \cdot \frac{Q}{r^2}    </math>.
Use the derived formula:
Our answer has the right units, since <math> \frac{1}{(\sqrt{x^2+ (L/2)^2})}    </math>. has the same units of <math>\frac{Q}{r^2}</math>
Is the direction qualitatively correct? We have the electric field pointing straight away from the midpoint of the rod, which is correct, given the symmetry of the situation. The vertical component of the electric field should indeed be zero.


== A Computational Model ==
<math>
E_y = \frac{Q}{4\pi\varepsilon_0 L y} \cdot \left( \frac{L/2}{\sqrt{(L/2)^2 + y^2}} \right)
</math>


'''Finding the Electric Field from a Rod with Code'''
Substitute known values:


Here is some code that you can run which shows the electric field vector
<math>
at a given distance from the rod along its length. The rod is shown as a
\varepsilon_0 = 8.85 \times 10^{-12} \, \text{C}^2/\text{Nm}^2
series of green balls to help emphasize that when using the numerical
</math>
integrations mentioned on this page, you are measuring the field produced
by discrete parts of the rod being analyzed.


Notice the edge-effects of the electric field of the rod. For reasons
<math>
discussed above, if we used the long rod approximation (L>>d), these
E_y = \frac{4.0 \times 10^{-6}}{4\pi(8.85 \times 10^{-12}) \cdot (2.0)(0.5)} \cdot \left( \frac{1.0}{\sqrt{1.0^2 + 0.5^2}} \right)
effects would be negligible.
</math>


[http://www.glowscript.org/#/user/yoderlukas/folder/Public/program/ElectricFieldAlongRodLength Click Here to Run the Code]
Evaluate:


==Examples==
<math>
E_y \approx 2.3 \times 10^5 \, \text{N/C}
</math>


Although this is not a very difficult topic, some reasonably difficult conceptual questions can be asked about it.
---


===Simple===
=== Example 3: Using the Simulation to Analyze Field Strength (Numerical/Visual) ===


[[Image:LukasYoderNo.jpg|400px|center|thumb|Figure1: Problem 1]]
Use the [Electric Field Along Rod Simulation](http://www.glowscript.org/#/user/yoderlukas/folder/Public/program/ElectricFieldAlongRodLength) to compare electric field strengths at two different points:


===Middling===
* Point A: Directly above the midpoint of the rod 
* Point B: The same distance above one of the rod’s ends


[[Image:LukasYoderMaybe.jpg|400px|center|thumb|Figure 2: Problem 2]]
'''Question:''' 
Which point has a stronger electric field? How does the field direction differ?


===Difficult===
'''Reflection:''' 
The field at Point A is stronger and points vertically due to symmetry. At Point B, the field is weaker and points diagonally inward toward the rod’s center. This shows the importance of symmetry in superposition, and helps illustrate “edge effects” that are harder to account for with algebra alone.


[[Image:LukasYoderYes.jpg|400px|center|thumb|Figure 3: Problem 3]]


== Connectedness ==
== Connectedness ==
The following two DIY experiments are shown to better understand and visualize the physical consequences of electric fields.


===Charged Rod and Aluminum Can===
At first glance, finding the electric field of a charged rod might just seem like a physics exercise, but it actually connects to a lot of real things — especially in aerospace.


In our first example we set up an experiment using two charged rods placed to the left and right of an aluminum can, distanced by a length d. If one of the rods is positively charged and the other is negatively charged, what will the can do? Because the positively charged rod induces a negative charge on the left side of the can, creating an attractive force between the rod and the can, and the negatively charged rod induces an equal positive charge on the right side of the can, which creates an attractive force between the can and that rod, the net force on the can is zero. Thus the can will stay still. The setup is depicted in the image below.
In spacecraft and satellites, components like power cables, structural booms, or tethers can hold charge and act basically like long rods. In space, charge builds up from sunlight or the plasma environment, and knowing how that charge creates electric fields helps engineers prevent issues like interference, arcing, or electrostatic discharge — which could damage sensitive electronics.


[[File:plusq.png|300px|center|thumb|Figure 4: apparatus diagram with +q]]
Even in aircraft, stuff like static wicks or long sensor probes can behave like charged rods, and their fields matter for things like EMC (electromagnetic compatibility). We need to make sure systems don’t interfere with each other, especially in environments where you’ve got a bunch of tightly packed electrical components.


Next, lets consider a setup but with both rods having equal positive charge, as shown in the image below. What will the can do in this situation?
As an AE major, I see this concept show up in ways I didn’t expect — whether it’s power systems on satellites, electrostatics in high-altitude flight, or how fields interact with composite materials. So yeah, we start with this simple charged rod, but the same physics applies all the way up to full-on orbital systems.


[[File:minusq.png|300px|center|thumb|Figure 5: apparatus diagram with -q]]


Again the can will also stay still, but this time it is because the polarization force between two objects is always attractive.
== History ==


So in what scenario will the can move, and what time of movement will the can exhibit? Considering the first setup, imagine this time we initially touch the negatively charged rod and the can for a brief moment. Holding the rods at equal distance on either side of the can, the can will now roll toward the positively charged rod. This is because the can acquires a net negative charge after being touched, so it is then attracted to the positively charged rod.
The idea that charged objects create electric fields has been around for a long time, but things really clicked in the 1700s when Charles-Augustin de Coulomb figured out how the force between charges actually worked. His experiments led to Coulomb’s Law, which became the foundation for electric field theory.


===Charged Rod and Pith Ball===
Back then, most experiments focused on point charges because they were easier to understand and measure. But over time, physicists realized that most real objects — wires, rods, surfaces — aren’t point-like. That’s where the idea of continuous charge distributions came in.


Another DIY experiment to visualize the effects of an electric field are shown in the video embedded below, which depicts the interaction between an initially neutral pith ball hanging on a string from a stand, and a charged rod.
The charged rod is one of the first examples you see when learning how to deal with this. It helps build the foundation for understanding more complex things like rings, disks, and eventually 3D shapes. Once you learn how to break up a rod into tiny charge pieces and add up their fields, you can start doing the same for almost any shape.
[http://www.youtube.com/watch?v=aeiqw81kGio Interaction between a Charged Rod and Pith Ball]


== History ==
It’s kind of cool to think that this whole section — which starts with drawing a little rod and doing some integrals — is part of the same chain of ideas that eventually leads to things like electric field simulations for spacecraft or antennas.


Physicists and scientists make use of electric fields and charged objects all the time. Many times, we may need to know which objects are contributing how much charge in certain areas. Charged objects may attract or repel (depending on the signs of their charge), so we often need to know how objects will interact with each other based on their charges. The phenomenon of this interaction, or electric force between charged particles, was finally confirmed and stated as a law in 1785 by French physicist Charles-Augustin de Coulomb, hence "Coulomb's Law."


== See also ==
== See also ==


The equation for the electric field of a charged rod was derived from the equation for an electric field of a charged particle. See the article "[[Electric Field]]" for more information.
The equation for the electric field of a charged rod was derived from the equation for the electric field of a charged particle. See the article "[[Electric Field]]" for more information.


=== Further Reading ===
=== Further Reading ===
Line 118: Line 223:


=== External Links ===
=== External Links ===
http://hyperphysics.phy-astr.gsu.edu/hbase/electric/elelin.html


http://online.cctt.org/physicslab/content/phyapc/lessonnotes/Efields/EchargedRods.asp
http://online.cctt.org/physicslab/content/phyapc/lessonnotes/Efields/EchargedRods.asp
Line 126: Line 232:


== References ==
== References ==
https://www.glowscript.org/#/
https://rhettallain_gmail_com.trinket.io/intro-to-electric-and-magnetic-fields#/electric-fields/multiple-charges


https://www.youtube.com/watch?v=BBWd0zUe0mI
https://www.youtube.com/watch?v=BBWd0zUe0mI


(For the above reference, I chose to follow the textbook's method in not defining the charge distribution and assuming it was constant, though this was helpful in figuring out a better way to introduce it.)
(For the above reference, the textbook's method is followed in that the charge distribution was left undefined, and assumed to be constant)


Chabay and Sherwood: Matter and Interactions, Fourth Edition, Chapter 15
Chabay and Sherwood: Matter and Interactions, Fourth Edition, Chapter 15


All figures created by author
 
[[Category: Electric Field]]
[[Category: Electric Field]]

Latest revision as of 17:05, 13 April 2025

Milo Karnes, Spring 2025

The Main Idea

In earlier studies, we learned about the electric field created by a point charge. However, in the real world, charges are often spread out over objects with shape and structure. One common example is a uniformly charged rod. To determine the electric field from such an object, we divide the rod into many infinitesimally small charge segments, treat each as a point charge, and integrate their contributions.

The key idea is to approximate the rod as a continuous line of charge using the principle of superposition. We consider the symmetry of the setup to simplify the problem and focus on the components of the electric field that don't cancel out.

The process of finding the electric field from a charged rod involves four main steps:

  1. Model the rod as many small charge elements and draw the electric field vector [math]\displaystyle{ \Delta \vec{E} }[/math] from a single element.
  2. Use symmetry to argue which components cancel and which remain.
  3. Integrate the contributions from all elements to find the net electric field.
  4. Verify that the result makes physical sense (units, direction, and limiting behavior).


A Mathematical Model

To calculate the electric field of a uniformly charged rod, we treat the rod as a continuous distribution of charge. Let the rod have total length [math]\displaystyle{ L }[/math] and total charge [math]\displaystyle{ Q }[/math], centered along the x-axis. The observation point is located on the y-axis a distance [math]\displaystyle{ y }[/math] above the center.

Step 1: Break the Rod into Pieces

We divide the rod into tiny segments of length [math]\displaystyle{ dx }[/math]. Each segment behaves like a point charge: [math]\displaystyle{ dq = \lambda \, dx }[/math], where [math]\displaystyle{ \lambda = \frac{Q}{L} }[/math] is the linear charge density.

Each [math]\displaystyle{ dq }[/math] contributes a small electric field [math]\displaystyle{ d\vec{E} }[/math] at the observation point.

Step 2: Write the Field Expression for One Piece

Using Coulomb’s Law, the electric field contribution from one element is:

[math]\displaystyle{ d\vec{E} = \frac{1}{4\pi\varepsilon_0} \cdot \frac{dq}{r^2} \cdot \hat{r} }[/math]

The vector from the source to the observation point is:

[math]\displaystyle{ \vec{r} = \langle 0, y \rangle - \langle x, 0 \rangle = \langle -x, y \rangle }[/math]

So:

[math]\displaystyle{ r = \sqrt{x^2 + y^2} \quad \text{and} \quad \hat{r} = \frac{\langle -x, y \rangle}{\sqrt{x^2 + y^2}} }[/math]

Putting it all together:

[math]\displaystyle{ d\vec{E} = \frac{1}{4\pi\varepsilon_0} \cdot \frac{\lambda \, dx}{(x^2 + y^2)} \cdot \frac{\langle -x, y \rangle}{\sqrt{x^2 + y^2}} = \frac{\lambda}{4\pi\varepsilon_0} \cdot \frac{\langle -x, y \rangle \, dx}{(x^2 + y^2)^{3/2}} }[/math]

Note: The x-components of the field cancel due to symmetry. Only the y-component adds up.

Step 3: Integrate

We now integrate from [math]\displaystyle{ -L/2 }[/math] to [math]\displaystyle{ +L/2 }[/math]:

[math]\displaystyle{ E_y = \frac{\lambda y}{4\pi\varepsilon_0} \int_{-L/2}^{L/2} \frac{dx}{(x^2 + y^2)^{3/2}} }[/math]

This integral has a standard solution:

[math]\displaystyle{ E_y = \frac{\lambda}{4\pi\varepsilon_0 y} \cdot \left( \frac{L/2}{\sqrt{(L/2)^2 + y^2}} \right) }[/math]

Final result:

[math]\displaystyle{ E_y = \frac{Q}{4\pi\varepsilon_0 L y} \cdot \left( \frac{L/2}{\sqrt{(L/2)^2 + y^2}} \right) }[/math]


Step 4: Check the Result

  • Units: The result has units of N/C, as expected.
  • Direction: The field points away from the rod if [math]\displaystyle{ Q \gt 0 }[/math], and toward the rod if [math]\displaystyle{ Q \lt 0 }[/math].
  • Limiting Behavior: As [math]\displaystyle{ y \gg L }[/math], the result simplifies to the electric field of a point charge:

[math]\displaystyle{ E \approx \frac{Q}{4 \pi \varepsilon_0 y^2} }[/math]


Computational Models

While symbolic solutions give us a deep understanding of how to derive the electric field, computational models allow us to visualize it in action. This is especially useful when dealing with continuous charge distributions like a uniformly charged rod.

GlowScript (a VPython-based simulation platform) makes it possible to numerically simulate and animate the electric field from a segmented rod. In these simulations, we treat the rod as a collection of small point charges, and compute the electric field vectors they produce at various locations in space.

Field Mapping Along the Rod's Length

In this first simulation, the rod is broken into a series of green spheres, each representing a small segment of uniform charge. At various points near the rod, electric field vectors are plotted to show how the strength and direction of the field change along and around the rod.

▶ Run Simulation: Electric Field Along Rod

Key takeaways:

  • Observe how the direction of the field changes based on position.
  • Near the center of the rod, the field is strongest and most symmetric.
  • Near the ends, the field vectors curve — an effect known as edge effects.
  • This illustrates why we often assume the rod is “infinitely long” in theory — to ignore those ends and simplify the math.

This tool is particularly helpful for developing intuition before solving test problems involving rods, wires, or even capacitors.

Radial Field Symmetry: Positive vs. Negative Charge

The next simulations demonstrate how the electric field behaves around a rod when it is positively or negatively charged. This is where direction matters — not just magnitude.

These models break the rod into 40 discrete segments and compute the net electric field throughout a 2D grid surrounding the rod.

Key observations:

  • Field lines from a positively charged rod point outward.
  • For a negatively charged rod, field lines point inward.
  • The symmetry is most noticeable when zoomed out — mimicking how an infinite line of charge behaves.
  • Near the ends, the distortion shows the importance of boundary conditions in real systems.

These are powerful tools when preparing for conceptual questions or visual reasoning tasks — they help make the math real.

Why It Matters

Computational models bridge the gap between the idealized math we do on paper and the messy, real-world systems we encounter in labs and engineering. They show us what electric fields actually look like when we account for discrete steps, edge effects, and variable observation points.

They’re also interactive — you can zoom in, rotate, and change parameters. When studying for exams, use these models to test your intuition: If a question asks you about the direction of a field, imagine running one of these and predicting what it would look like.

All simulations above are written using GlowScript (VPython), and are free to edit or remix as part of your own projects or demonstrations.


Examples

These examples cover different levels of conceptual and quantitative understanding of the electric field due to a uniformly charged rod. Try using the computational models above to visualize your answers!

Example 1: Symmetry and Direction (Conceptual)

You are observing a positively charged rod lying along the x-axis, centered at the origin. You stand at a point on the y-axis a distance [math]\displaystyle{ y }[/math] above the midpoint of the rod.

Question: What direction does the electric field point at your location?

Answer: The horizontal components of the field from symmetric charge elements cancel, and only the vertical (y-direction) components add constructively. Therefore, the electric field points directly upward (in the +y direction) if the rod is positively charged.


Example 2: Deriving the Field at a Point (Symbolic)

A rod of total length [math]\displaystyle{ L = 2.0 \, \text{m} }[/math] carries a total charge [math]\displaystyle{ Q = 4.0 \times 10^{-6} \, \text{C} }[/math]. It lies along the x-axis, centered at the origin. Find the magnitude of the electric field at a point [math]\displaystyle{ y = 0.5 \, \text{m} }[/math] directly above its center.

Solution:

Use the derived formula:

[math]\displaystyle{ E_y = \frac{Q}{4\pi\varepsilon_0 L y} \cdot \left( \frac{L/2}{\sqrt{(L/2)^2 + y^2}} \right) }[/math]

Substitute known values:

[math]\displaystyle{ \varepsilon_0 = 8.85 \times 10^{-12} \, \text{C}^2/\text{Nm}^2 }[/math]

[math]\displaystyle{ E_y = \frac{4.0 \times 10^{-6}}{4\pi(8.85 \times 10^{-12}) \cdot (2.0)(0.5)} \cdot \left( \frac{1.0}{\sqrt{1.0^2 + 0.5^2}} \right) }[/math]

Evaluate:

[math]\displaystyle{ E_y \approx 2.3 \times 10^5 \, \text{N/C} }[/math]

---

Example 3: Using the Simulation to Analyze Field Strength (Numerical/Visual)

Use the [Electric Field Along Rod Simulation](http://www.glowscript.org/#/user/yoderlukas/folder/Public/program/ElectricFieldAlongRodLength) to compare electric field strengths at two different points:

  • Point A: Directly above the midpoint of the rod
  • Point B: The same distance above one of the rod’s ends

Question: Which point has a stronger electric field? How does the field direction differ?

Reflection: The field at Point A is stronger and points vertically due to symmetry. At Point B, the field is weaker and points diagonally inward toward the rod’s center. This shows the importance of symmetry in superposition, and helps illustrate “edge effects” that are harder to account for with algebra alone.


Connectedness

At first glance, finding the electric field of a charged rod might just seem like a physics exercise, but it actually connects to a lot of real things — especially in aerospace.

In spacecraft and satellites, components like power cables, structural booms, or tethers can hold charge and act basically like long rods. In space, charge builds up from sunlight or the plasma environment, and knowing how that charge creates electric fields helps engineers prevent issues like interference, arcing, or electrostatic discharge — which could damage sensitive electronics.

Even in aircraft, stuff like static wicks or long sensor probes can behave like charged rods, and their fields matter for things like EMC (electromagnetic compatibility). We need to make sure systems don’t interfere with each other, especially in environments where you’ve got a bunch of tightly packed electrical components.

As an AE major, I see this concept show up in ways I didn’t expect — whether it’s power systems on satellites, electrostatics in high-altitude flight, or how fields interact with composite materials. So yeah, we start with this simple charged rod, but the same physics applies all the way up to full-on orbital systems.


History

The idea that charged objects create electric fields has been around for a long time, but things really clicked in the 1700s when Charles-Augustin de Coulomb figured out how the force between charges actually worked. His experiments led to Coulomb’s Law, which became the foundation for electric field theory.

Back then, most experiments focused on point charges because they were easier to understand and measure. But over time, physicists realized that most real objects — wires, rods, surfaces — aren’t point-like. That’s where the idea of continuous charge distributions came in.

The charged rod is one of the first examples you see when learning how to deal with this. It helps build the foundation for understanding more complex things like rings, disks, and eventually 3D shapes. Once you learn how to break up a rod into tiny charge pieces and add up their fields, you can start doing the same for almost any shape.

It’s kind of cool to think that this whole section — which starts with drawing a little rod and doing some integrals — is part of the same chain of ideas that eventually leads to things like electric field simulations for spacecraft or antennas.


See also

The equation for the electric field of a charged rod was derived from the equation for the electric field of a charged particle. See the article "Electric Field" for more information.

Further Reading

The page on electric fields: Electric Field

External Links

http://hyperphysics.phy-astr.gsu.edu/hbase/electric/elelin.html

http://online.cctt.org/physicslab/content/phyapc/lessonnotes/Efields/EchargedRods.asp

https://pages.uncc.edu/phys2102/online-lectures/chapter-02-electric-field/2-4-electric-field-of-charge-distributions/example-1-electric-field-of-a-charged-rod-along-its-axis/

http://dev.physicslab.org/Document.aspx?doctype=3&filename=Electrostatics_ContinuousChargedRod.xml

References

https://www.glowscript.org/#/

https://rhettallain_gmail_com.trinket.io/intro-to-electric-and-magnetic-fields#/electric-fields/multiple-charges

https://www.youtube.com/watch?v=BBWd0zUe0mI

(For the above reference, the textbook's method is followed in that the charge distribution was left undefined, and assumed to be constant)

Chabay and Sherwood: Matter and Interactions, Fourth Edition, Chapter 15

Retrieved from "http://www.physicsbook.gatech.edu/index.php?title=Field_of_a_Charged_Rod&oldid=47122"