Ohm's Law

This page was created by Max Trussell, username: mtrussell6

Ohm's law is a very famous equation discovered by Georg Ohm describing the proportional relationship between voltage and current through some conductor. Most commonly this equation is seen in the form of

, with I representing current in amperes, V representing electric potential in volts, and R the resistance in ohms.

The Main Idea

Stripped down to its most basic, Ohm's Law exists so that either the electric potential, current, or total resistance of some conductor may be found when two out of the three are known quantities. This is possible because of the simple, linear relationship between the three.

A simple Ohmic circuit displaying I, V, and R as relevant to Ohm's Law. Source: reference 1

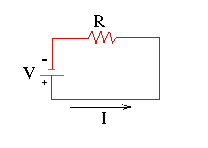
A Mathematical Model

While most often represented as [math]\displaystyle{ {I = \frac{|\Delta V|}{R}} }[/math], Ohm's Law may also be represented as [math]\displaystyle{ V = IR }[/math] or [math]\displaystyle{ {R = \frac{V}{I}} }[/math]. Noteworthy is the fact that Ohm's Law depends upon Ohmic resistance and near ideal conductors to be accurate. Fortunately, most simple circuits without capacitance or inductance fit this criteria as the wires offer minuscule resistance when compared to the various resistors in the circuit. Additionally at any given point in time, Ohm's Law applies to both alternating current and direct current. Also worth noting is that V does not necessarily represent the potential difference across a single source of electric potential (e.g. a battery) but rather the absolute value of the potential difference across an entire circuit.

A Computational Model

There are numerous programs to be found that simulate circuits via Ohm's Law, with many allowing for analysis beyond the standard scope of Ohm's Law. One such example is Phet's Circuit Construction Kit, a free, lightweight tool to create and analyze simple DC current circuits. Here is a video briefly describing its installation and use!

Examples

Simple

The most basic example of Ohm's Law in action involves a closed circuit with a single power source and a single Ohmic resistor.

Image Source: Max Trussell

For this example the power source will be 12 volts and the resistor will be 4 ohms. To solve for the current, simply plug in the given values to get [math]\displaystyle{ {\frac{12V}{4\Omega} = 3A} }[/math], meaning that the current is 3 amperes.

Middling

A slightly more complex example involves a closed circuit with a single power source and two Ohmic resistors in parallel.

Image Source: reference 2

In this case, R₁ is given to be 2 ohms, R₂ is given to be 4 ohms, and I is given to be 3 amperes. The first step is to remember that the R in the Ohm's Law equation represents total resistance, not individual resistors. In this case (Ohmic resistors in parallel), [math]\displaystyle{ {\frac{1}{R_{Net}} = \frac{1}{R_{1}} + \frac{1}{R_{2}}} }[/math], plug in R₁ and R₂ to find [math]\displaystyle{ R_{Net} = \frac{4}{3} \Omega }[/math].

Now using the form of Ohm's Law [math]\displaystyle{ V = IR }[/math], plug in known values to get [math]\displaystyle{ (3A)(\frac{4}{3}\Omega) = 4V }[/math], so the electric potential across this circuit has been shown to be 4 volts.

Difficult

A more challenging application of Ohm's Law involves a closed circuit with two identical power sources connected in series to three resistors, two of which are in parallel.

Image Source: Max Trussell

Step 1: Find the Total Resistance

The total resistance for this circuit is going to equal the resistance of R₁ plus the resistance of R₂ and R₃ in parallel. Using the equation from the previous problem, [math]\displaystyle{ {\frac{1}{R_{P}} = \frac{1}{R_{2}} + \frac{1}{R_{3}}} }[/math], plug in R₂ and R₃ to get [math]\displaystyle{ R_{P} = 2.4\Omega }[/math]

Then for total resistance, R_P must be added to R₁ to get [math]\displaystyle{ 2.4\Omega + 2\Omega = 4.4\Omega }[/math]

Step 2: Find the Total Voltage

The total voltage for this circuit in this case is simply equal to the voltages of each power source added together, meaning [math]\displaystyle{ V_{T} = 2(4V) = 8V }[/math]

Step 3: Plug Into Appropriate Version of Ohm's Law

Now just plug the total resistance and voltage into [math]\displaystyle{ I = \frac{V}{R} }[/math] to get a current of 1.82 amperes

Connectedness

1. How is this topic connected to something that you are interested in?
   Ohm's Law is the premise on which all simple circuits are created, meaning it is the foundation of nearly all modern electronics! Without Ohm's Law, there would be no cellphones, laptops, or even outlets in the wall.

1. How is it connected to your major?
   As a computer scientist, in all likelihood I will not be directly using Ohm's Law for my work, but as stated previously, without it there would be no computers and thus, no computer science.

1. Is there an interesting industrial application?
   Nearly all modern industry relies on electronics, from an assembly line to the lights in a small cafe. It is safe to say that without Ohm's Law, nearly every facet of modern industry would be dramatically different!

History

Back in 1827, German physicist Georg Ohm published his most recent work on resistance in electric circuits. In this work, entitled Die galvanische Kette, mathematisch bearbeitet, he first unveiled what is now know as Ohm's Law. Unfortunately due to political reasons, his work was never considered seriously until the 1840s and 1850s, at which point it became the leading theory on resistance in circuits, beating out rivals such as Barlow's Law. Ohm's work on both Ohm's Law and Ohmic resistors layed the foundations for contemporary circuitry and opened the gates to further scientific discoveries regarding the flow of electricity!

See also

• Current
• Loop Rule
• Voltage

Further reading

• Matter and Interactions, 4th Edition, Chapters 18 and 19
• Calculus Based Physics II by Jeffrey Shnick, free textbook--downloadable here

External links

• Physics Classroom on Ohm's Law
• Hyper Physics on Ohm's Law

References

1. Basic Circuit. Digital image. Plattsburgh. N.p., n.d. Web
2. Circuit With Parallel Resistors. Digital image. Cambridge University Department of Engineering and Biotechnology. N.p., n.d. Web.
3. "Ohm's Law." Ohm's Law. N.p., n.d. Web. 05 Dec. 2015.
4. Chabay, Ruth W., and Bruce A. Sherwood. "Circuit Elements." Matter and Interactions, 4th Edition. N.p.: n.p., 2015. 783-99. Print.