Talk:Main Page: Difference between revisions

Latest revision as of 20:36, 26 November 2016

Torque -

Torque is a Latin word that roughly means "twist," and is usually symbolized by the lower case Greek letter tau. Torque is the measurement of how much a force, F, acting on an object will cause that object to rotate. This force is usually applied to an arm of some sort that is attached to a fulcrum or pivot point. For example, using a wrench to loosen or tighten a nut requires the use of torque - where the wrench would be the arm you apply the force to and the nut would be the pivot point that the force rotates around.

The Main Idea

In "Matter & Interactions, Fourth Edition," torque is defined as τ = r_A x F . Applying a torque to an object changes the angular momentum of that object. Torque, in angular momentum calculations, is analogus to F_net in regular momentum calculations. Just like how a collection of forces acting on a system is called F_net, a collection of torques acting on a system is τ_net.

A Mathematical Model

Torque is defined as the cross product of the distance vector, the distance from pivot point to the location of the applied force, with an applied force. The magnitude of torque can be defined as such:

τ_A = r_AFsinθ

Torque can also be defined as τ = dL/dt , or the derivative of angular momentum, L. To determine the direction of torque, one can either compute the cross product or apply the "right-hand rule." To use the "right-hand rule," point your fingers in the direction of r_A and curl your fingers in the direction of F.

If your thumb points up, the force is coming out of the page and is in the positive z-directon. If your thumb points down, the force is going into the page and is in the negative z-direction.

A Computational Model

The above picture is a great example of what torque would look like in the real world. To make a similar simulation in vpython, all you would need to do is update position and angular momentum. The code would look something like this:

While t<some number:

L=L+tnet*deltat

v=L/mass

r=r+v*deltat

t=t+deltat

Where L is your angular momentum initialized earlier, tnet is total torque, deltat is your time step, and r is your original location.

Examples

Be sure to show all steps in your solution and include diagrams whenever possible

Simple

In a hurry to catch a cab, you rush through a frictionless swinging door and onto the sidewalk. The force you extered on the door was 50N, applied perpendicular to the plane of the door. The door is 1.0m wide. Assuming that you pushed the door at its edge, what was the torque on the swinging door (taking the hinge as the pivot point)?

(50N)(1.0m)sin(90) = 50 Nm

Middling

A uniform solid disk with radius 9 cm has mass 0.5 kg (moment of inertia I = ½MR2). A constant force 12 N is applied as shown. At the instant shown, the angular velocity of the disk is 25 radians/s in the −z direction (where +x is to the right, +y is up, and +z is out of the page, toward you). The length of the string d is 14 cm.

What are the magnitude and direction of the torque on the disk, about the center of mass of the disk?

(12N)(0.09m)= 1.08 Nm

Direction: -z direction because of the right hand rule

Difficult

We want to place another mass on the see-saw to keep the see-saw from tipping. The only other one we have is a 5.0kg mass. Where would we place this to balance the original 3kg mass that was placed 2.00m to the right of the pivot point?

(3kg)(9.8 m/s^2)(2.00m) = (5kg)(9.8 m/s^2)(x)

58.8 = 49x

x=1.2

Connectedness

How is this topic connected to something that you are interested in? I have a heavy interest in cars. More specifically, I love race cars, and I love watching Formula1, BTCC, WRC, and other car racing series. Torque, in cars, gives you an idea of how fast the car can accelerate. But more importantly, torque can make cars do this:

and this:

How is it connected to your major?

Torque is heavily related to mechanical engineering. Whether it be driving a conveyor belt in a factor, a driveshaft in a car, turning a wrench, or otherwise, torque is involved in almost all mechanical systems. Mechanical engineers use torque to transform energy into a useful form. For example, they use torque in electric motors to turn electric energy into rotational energy that can be used in all sorts of appliances. Mechanical engineers also take the chemical energy from gasoline combustion and turn it into torque to power planes, trains, and automobiles. Torque is applicable in all types of engineering.

Is there an interesting industrial application?

The amount of industrial applications of torque is nearly infinite, but one machine I find interesting is the lathe. The lathe uses torque and rotation to shape various materials [1]

History

The idea of torque originated with Archimedes studies on levers. Archimedes may not have invented the lever, but he was one of the first scientists to investigate how they work in 241 BC.

Circuits (R, LC, RL)

Circuit Elements

In terms of physics, an electrical circuit is a system which is composed of certain combinations of circuit elements, including resistors, capacitors, and inductors. When used in different combinations, these elements create R, LC, RL, RC circuits. The elements that make up these circuits include capacitors, resistors, batteries, ammeters, voltmeters, ohmmeters. When an electric field is applied to a conductor, the mobile charges in the conductor experience forces, and to move in the direction of those forces. Active circuits do not experience equilibrium, rather they experience a steady state in which means that charges are moving, but their drift velocities do not change with time. For circuits, equilibriums means that there is no current flowing.

Contents [hide] 1 The Main Idea 1.1 A Mathematical Model 1.2 A Computational Model 2 Examples 2.1 Simple 2.2 Middling 2.3 Difficult 3 Connectedness 4 History 5 See also 5.1 Further reading 5.2 External links 6 References The Main Idea To create an active circuit there must be a specific combination of the elements above as well as a nonzero electric field in the wires. The direction of the electric field at every location must be along the wire since the current flow follows the wire. According to the loop rule, energy must be conserved along any closed path in a circuit. Although, using resistors, capacitors, ammeters, voltmeters, ohmmeters, and batteries the flow of current can change with time.

A Mathematical Model In the steady state the net electron current can be shown in the equation: i=nAuE

the conventional current can be solved for through the equation: I=|q|nAuE

Energy conservation (the loop rule): Net change in potential=0

A Computational Model /Users/maggiegarratt/Desktop/Screen Shot 2015-12-05 at 6.45.05 PM.jpg A proton moving in a circular motion parallel to the xz plane. Because the particle has both an and y component of velocity, the particles path is a helix.

Example 1

Solve for the current in the resistor:

[File:/Users/maggiegarratt/Desktop/simple.jpg]

Example 2

[File:/Users/maggiegarratt/Desktop/Screen Shot 2015-12-05 at 7.59.03 PM.jpg]

Example

[File:/Users/maggiegarratt/Desktop/Screen Shot 2015-12-05 at 7.56.37 PM.jpg]

Circuits provide the world with many conveniences. From simple circuits within flashlights to parallel circuits in household lighting everyday life is made simpler because of their existence. The difference between parallel and series circuits can be noted through the reaction of Christmas lights to a bulb burning out. If a bulb burns out in a series circuit the entire string of lights will burn out as well. This is because in a series circuit there is only one pathway for the current to flow. When the pathway is disrupted the current is in equilibrium and stops flowing. On the other hand, if a bulb burns out and the remaining bulbs stay lit you know they are connected through a parallel circuit. When the bulbs are connected in parallel there are multiple alternate pathways for the currents to travel in.

Many careers necessitate an in-depth knowledge of circuits. For the major of mechanical engineering a knowledge of circuits is beneficial for multiple applications. When designing electronic technologies it is necessary to understand the circuitry within the design.

History Early investigations of static electricity go back hundreds of years. Static electricity is a transfer of electrons produced by friction, like when you rub a balloon across a sweater. A spark or very brief flow of current can occur when charged objects come into contact, but there is no continuous flow of current. In the absence of a continuous current, there is no useful application of electricity. The invention of the battery -- which could produce a continuous flow of current -- made possible the development of the first electric circuits. Alessandro Volta invented the first battery, the voltaic pile, in 1800. The very first circuits used a battery and electrodes immersed in a container of water. The flow of current through the water produced hydrogen and oxygen. The first widespread application of electric circuits for practical use was for electric lighting. Shortly after Thomas Edison invented his incandescent light bulb, he sought practical applications for it by developing an entire power generation and distribution system. The first such system in the United States was the Pearl Street Station in downtown Manhattan. It provided a few square blocks of the city with electric power, primarily for illumination. One classification of circuits has to do with the nature of the current flow. The earliest circuits were battery-powered, which made in a steady, constant current that always flowed in the same direction. This is direct current, or DC. The use of DC continued through the time of the first electric power systems. A major problem with the DC system was that power stations could serve an area of only about a square mile because of power loss in the wires. In 1883, engineers proposed harnessing the tremendous hydroelectric power potential of Niagara Falls to supply the needs of Buffalo, N.Y. Although this power would ultimately go beyond Buffalo to New York City and even farther, there was an initial problem with distance. Buffalo was only 16 miles from Niagara Falls, but the idea was unworkable -- until Nikola Tesla made it possible, as we'll see on the next page.

See also Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?

@@ Line 1: / Line 1: @@
-== Why Energy is conserved  ==
+== Torque - ==
-The main idea of this page is to elaborate a little more on why energy is conserved and to understand it is a more simplified way. The thought about the fact that energy is neither created nor destroyed can be a mind boggling one simply because energy always seems to be coming from somewhere, so where does it go? The main idea behind why energy is conserved and neither created or destroyed is that it is just transferred to other forms. The first law of Thermodynamics states that the amount of energy in the universe is a constant, fixed amount. Is doesn’t go away and it doesn’t appear randomly.
+Torque is a Latin word that roughly means "twist," and is usually symbolized by the lower case Greek letter tau. Torque is the measurement of how much a force, F, acting on an object will cause that object to rotate. This force is usually applied to an arm of some sort that is attached to a fulcrum or pivot point. For example, using a wrench to loosen or tighten a nut requires the use of torque - where the wrench would be the arm you apply the force to and the nut would be the pivot point that the force rotates around.
+[[File:wrench_gif.gif]]
+==The Main Idea==
+In "Matter & Interactions, Fourth Edition," torque is defined as &tau; = r<sub>A</sub> x F .
+Applying a torque to an object changes the angular momentum of that object. Torque, in angular momentum calculations, is analogus to F<sub>net</sub> in regular momentum calculations. Just like how a collection of forces acting on a system is called F<sub>net</sub>, a collection of torques acting on a system is &tau;<sub>net</sub>.
 ===A Mathematical Model===
-The mathematical equations that are used to model this topic include many different equations, but they all relate back to the energy principle, ΔEsystem = WSurr +Q. W is the work cone by the surroundings and Q is the thermal energy. The change in energy will be always zero because energy is transferring to other forms of energy within the system or surroundings. Other Important equations include:
+[[File:torque_diagram.gif]]
-K = ½mv2, ΔUg = mgΔh, E = K + U, Ei = Ef, Ki + Ui = Kf  + Uf, W = F̅Δs cos θ.
+Torque is defined as the cross product of the distance vector, the distance from pivot point to the location of the applied force, with an applied force. The magnitude of torque can be defined as such:
+*&tau;<sub>A</sub> = r<sub>A</sub>Fsin&theta;
+Torque can also be defined as &tau; = dL/dt  , or the derivative of angular momentum, L.
+To determine the direction of torque, one can either compute the cross product or apply the "right-hand rule." To use the "right-hand rule," point your fingers in the direction of r<sub>A</sub> and curl your fingers in the direction of F.
+[[File:Rhr_torque.JPG]]
+If your thumb points up, the force is coming out of the page and is in the positive z-directon. If your thumb points down, the force is going into the page and is in the negative z-direction.
 ===A Computational Model===
-This video shows how energy in conserved in a variety of situations.
-http://study.com/academy/lesson/first-law-of-thermodynamics-law-of-conservation-of-energy.html
+[[File:Torque.gif]]
+The above picture is a great example of what torque would look like in the real world. To make a similar simulation in vpython, all you would need to do is update position and angular momentum. The code would look something like this:
+While t<some number:
+L=L+tnet*deltat
+v=L/mass
+r=r+v*deltat
+t=t+deltat
+Where L is your angular momentum initialized earlier, tnet is total torque, deltat is your time step, and r is your original location.
 ==Examples==
+Be sure to show all steps in your solution and include diagrams whenever possible
 ===Simple===
-Question:   State the law of conservation of energy and explain the law by taking an oscillating simple pendulum as an example.
-Answer:    The law of conservation of energy says that energy can neither be created nor destroyed but can be transformed from one form to another.
+In a hurry to catch a cab, you rush through a frictionless swinging door and onto the sidewalk. The force you extered on the door was 50N, applied perpendicular to the plane of the door. The door is 1.0m wide. Assuming that you pushed the door at its edge, what was the torque on the swinging door (taking the hinge as the pivot point)?
-In the case of the simple pendulum when the bob is as far to the left as it can be, it has maximum potential energy as it is raised with respect to the mean position, but its kinetic energy is zero as the bob stops oscillating for a fraction of a second before moving towards the right. When the bob reaches the mean position, it has a zero potential energy but maximum kinetic energy (maximum velocity too). When the bob of the pendulum swings to extreme right, it has the maximum potential energy but zero kinetic energy.
+[[File:torqueE1.gif]]
+(50N)(1.0m)sin(90) = 50 Nm
 ===Middling===
-Question:   A nail becomes warm when it is hammered into a plank. Explain why.
-Answer:    A raised hammer has potential energy due to its position above the ground, gravity acts as acceleration. When the hammer comes down and strikes the head of the nail, the potential energy is transformed into kinetic energy. If we continue hitting the nail to secure it, the kinetic energy of the hammer is transferred to the molecules of the material of the nail. The heat content of the body is the total energy that the body possesses (Q in the equation above). As the heat content of the body increases, the nail becomes warm.
+A uniform solid disk with radius 9 cm has mass 0.5 kg (moment of inertia I = ½MR2). A constant force 12 N is applied as shown. At the instant shown, the angular velocity of the disk is 25 radians/s in the −z direction (where +x is to the right, +y is up, and +z is out of the page, toward you). The length of the string d is 14 cm.
+[[File:disk torque.jpg]]
+What are the magnitude and direction of the torque on the disk, about the center of mass of the disk?
+(12N)(0.09m)= 1.08 Nm
+Direction: -z direction because of the right hand rule
 ===Difficult===
-Question:
-A stone of mass 10 g placed at the top of a tower 50 m high is allowed to fall freely. Show that law of conservation of energy holds good in the case of the stone.
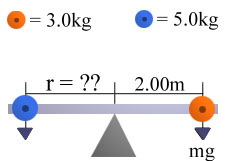
+We want to place another mass on the see-saw to keep the see-saw from tipping. The only other one we have is a 5.0kg mass. Where would we place this to balance the original 3kg mass that was placed 2.00m to the right of the pivot point?
-http://images.tutorvista.com/contentimages/science/CBSEIXSCIENCE/Ch146/images/img179.jpeg
-Answer: In this case we have to prove that total energy at A, B and C is the same.
+[[File:prob2.jpg]]
-Height = 50 m
-Potential energy at A = mgh
+(3kg)(9.8 m/s^2)(2.00m) = (5kg)(9.8 m/s^2)(x)
-= 0.01 x 9.8 x 50
-= 0.01 x 98 x 5
+.8 = 49x
-= 4.9 J
-= 0
+x=1.2
-Total energy at A = potential energy + kinetic energy= 4.9 + 0
-Total energy at A = 4.9 J ...(1)
-At B
-Height from the ground = 40 m
-Potential energy = mgh
-= 0.01 x 9.8 x 40
-= 0.01 x 98 x 4
-Potential energy at B = 3.92 J
-To calculate v we make use of III equation of motion,
-Here, u = 0, a = 9.8 m/s2 and H = 10 m
-= 0.98 J
-Total energy at B = potential energy + kinetic energy
-= 3.92 + 0.98
-Total energy at B = 4.90 J (2)
-At C
-Height from the ground = 0
-Potential energy at C = mgh
-To calculate v we use III equation of motion,
-Here, u = 0, a = 9.8m/s2 and H = 50 m
-= 4.9 J
-Total energy at C = potential energy + kinetic energy
-= 0 + 4.9
-Total energy at C = 4.9 J (3)
-The total energy at A, B and C is 4.9 J. This means that law of conservation of energy holds good in the case of a stone falling freely under gravity.
 ==Connectedness==
-#I am interested in this topic because Physics has never really clicked in my mind and researching more on why when you do work on a system the energy is conserved is very interesting to me. I learned a lot why doing this and now understand why this is true instead of just memorizing that it is true.
+How is this topic connected to something that you are interested in?
-# This is connected to my major because I am a Biology/Pre-Health major and I am interested in making medical products that increase the efficiently of hospitals. This concept can be important because I will want to design products that use as a little energy as possible while still getting the job done effectively.
+I have a heavy interest in cars. More specifically, I love race cars, and I love watching Formula1, BTCC, WRC, and other car racing series. Torque, in cars, gives you an idea of how fast the car can accelerate. But more importantly, torque can make cars do this:
-#The industrial application that can be used concerning this topic is that certain materials can be used when building structures to minimize thermal energy lost, thus making the system more effective.
+[[File:burnout_loop.gif]]
+and this:
+[[File:corvetteburnout.gif]]
+How is it connected to your major?
+Torque is heavily related to mechanical engineering. Whether it be driving a conveyor belt in a factor, a driveshaft in a car, turning a wrench, or otherwise, torque is involved in almost all mechanical systems. Mechanical engineers use torque to transform energy into a useful form. For example, they use torque in electric motors to turn electric energy into rotational energy that can be used in all sorts of appliances. Mechanical engineers also take the chemical energy from gasoline combustion and turn it into torque to power planes, trains, and automobiles. Torque is applicable in all types of engineering.
+Is there an interesting industrial application?
+The amount of industrial applications of torque is nearly infinite, but one machine I find interesting is the lathe. The lathe uses torque and rotation to shape various materials   [https://www.youtube.com/watch?v=9qt5ui3P9QA]
 ==History==
-There are many people who contributed to the Conservation of Energy laws. In 1639 Galileo, who was from Italy, introduced the pendulum where potential and kinetic energy are always present in different amounts throughout the motion. French physicists Gottfried Wilhelm Leibniz formulated how Kinetic energy is connected to velocity and mass between 1676-1689. How kinetic energy and Work are related was described by Gaspard-Gustave Coriolis and Jean-Victor Poncelet from 1819-1839 in France. All of these men, along with many others played a very important role in formulating what we know about energy today and they did is because they were constantly trying to make improvements to society and science.
+The idea of torque originated with Archimedes studies on levers. Archimedes may not have invented the lever, but he was one of the first scientists to investigate how they work in 241 BC.
+== See also ==
+[https://en.wikipedia.org/wiki/Torque]
+[https://www.physics.uoguelph.ca/tutorials/torque/Q.torque.intro.html]
-== See also ==
-More practice problems: http://www.tutorvista.com/content/science/science-i/work-energy/question-answers-2.php#question-21
 ===Further reading===
-One book I found interesting on this topic is called ''Energy, Society, and Environment: Technology for a Sustainable Future'' ''Italic text''by David Elliott. This book talks about connecting the conservation of energy principles that have bee around for a long time to modern technology
+Books, Articles or other print media on this topic
 ===External links===
+[http://www.scientificamerican.com/article/bring-science-home-reaction-time/]
+[https://en.wikipedia.org/wiki/Torque
+[https://www.physics.uoguelph.ca/tutorials/torque/Q.torque.intro.html]]
+[http://hyperphysics.phy-astr.gsu.edu/hbase/torq.html]
+==References==
+This section contains the the references you used while writing this page
+[[https://en.wikipedia.org/wiki/Torque]]
+[http://hyperphysics.phy-astr.gsu.edu/hbase/torq.html]
+[https://www.physics.uoguelph.ca/tutorials/torque/Q.torque.intro.html]
+[[Category:Angular Momentum]]
-This link provides very good information about the conservation of energy http://hyperphysics.phy-astr.gsu.edu/hbase/conser.html
+== Circuits (R, LC, RL) ==
-==References==
+Circuit Elements
-http://study.com/academy/lesson/first-law-of-thermodynamics-law-of-conservation-of-energy.html http://www.tutorvista.com/content/science/science-i/work-energy/question-answers-2.php#question-21
-https://en.wikipedia.org/wiki/Conservation_of_energy#History
+In terms of physics, an electrical circuit is a system which is composed of certain combinations of circuit elements, including resistors, capacitors, and inductors. When used in different combinations, these elements create R, LC, RL, RC circuits. The elements that make up these circuits include capacitors, resistors, batteries, ammeters, voltmeters, ohmmeters. When an electric field is applied to a conductor, the mobile charges in the conductor experience forces, and to move in the direction of those forces. Active circuits do not experience equilibrium, rather they experience a steady state in which means that charges are moving, but their drift velocities do not change with time. For circuits, equilibriums means that there is no current flowing.
+Contents [hide]
+The Main Idea
+.1 A Mathematical Model
+.2 A Computational Model
+Examples
+.1 Simple
+.2 Middling
+.3 Difficult
+Connectedness
+History
+See also
+.1 Further reading
+.2 External links
+References
+The Main Idea
+To create an active circuit there must be a specific combination of the elements above as well as a nonzero electric field in the wires. The direction of the electric field at every location must be along the wire since the current flow follows the wire. According to the loop rule, energy must be conserved along any closed path in a circuit. Although, using resistors, capacitors, ammeters, voltmeters, ohmmeters, and batteries the flow of current can change with time.
+A Mathematical Model
+In the steady state the net electron current can be shown in the equation:
+i=nAuE
+the conventional current can be solved for through the equation:
+I=|q|nAuE
+Energy conservation (the loop rule):
+Net change in potential=0
+A Computational Model
+[[/Users/maggiegarratt/Desktop/Screen Shot 2015-12-05 at 6.45.05 PM.jpg]]
+A proton moving in a circular motion parallel to the xz plane. Because the particle has both an  and y component of velocity, the particles path is a helix.
+Example 1
+Solve for the current in the resistor:
+[File:/Users/maggiegarratt/Desktop/simple.jpg]
+Example 2
+[File:/Users/maggiegarratt/Desktop/Screen Shot 2015-12-05 at 7.59.03 PM.jpg]
+Example
+[File:/Users/maggiegarratt/Desktop/Screen Shot 2015-12-05 at 7.56.37 PM.jpg]
+Circuits provide the world with many conveniences. From simple circuits within flashlights to parallel circuits in household lighting everyday life is made simpler because of their existence. The difference between parallel and series circuits can be noted through the reaction of Christmas lights to a bulb burning out. If a bulb burns out in a series circuit the entire string of lights will burn out as well. This is because in a series circuit there is only one pathway for the current to flow. When the pathway is disrupted the current is in equilibrium and stops flowing. On the other hand, if a bulb burns out and the remaining bulbs stay lit you know they are connected through a parallel circuit. When the bulbs are connected in parallel there are multiple alternate pathways for the currents to travel in.
+Many careers necessitate an in-depth knowledge of circuits. For the major of mechanical engineering a knowledge of circuits is beneficial for multiple applications. When designing electronic technologies it is necessary to understand the circuitry within the design.
+History
+Early investigations of static electricity go back hundreds of years. Static electricity is a transfer of electrons produced by friction, like when you rub a balloon across a sweater. A spark or very brief flow of current can occur when charged objects come into contact, but there is no continuous flow of current. In the absence of a continuous current, there is no useful application of electricity.
+The invention of the battery -- which could produce a continuous flow of current -- made possible the development of the first electric circuits. Alessandro Volta invented the first battery, the voltaic pile, in 1800. The very first circuits used a battery and electrodes immersed in a container of water. The flow of current through the water produced hydrogen and oxygen.
+The first widespread application of electric circuits for practical use was for electric lighting. Shortly after Thomas Edison invented his incandescent light bulb, he sought practical applications for it by developing an entire power generation and distribution system. The first such system in the United States was the Pearl Street Station in downtown Manhattan. It provided a few square blocks of the city with electric power, primarily for illumination.
+One classification of circuits has to do with the nature of the current flow. The earliest circuits were battery-powered, which made in a steady, constant current that always flowed in the same direction. This is direct current, or DC. The use of DC continued through the time of the first electric power systems. A major problem with the DC system was that power stations could serve an area of only about a square mile because of power loss in the wires.
+In 1883, engineers proposed harnessing the tremendous hydroelectric power potential of Niagara Falls to supply the needs of Buffalo, N.Y. Although this power would ultimately go beyond Buffalo to New York City and even farther, there was an initial problem with distance. Buffalo was only 16 miles from Niagara Falls, but the idea was unworkable -- until Nikola Tesla made it possible, as we'll see on the next page.
+See also
+Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?
+Further reading
+The Art of ElectronicsApr 9, 2015
+by Paul Horowitz and Winfield Hill
+Practical Electronics for Inventors, Third Edition Jan 31, 2013
+by Paul Scherz and Simon Monk
+Make: Electronics: Learning Through Discovery Sep 7, 2015
+by Charles Platt
+External links:
+https://www.khanacademy.org/science/physics/circuits-topic
+https://learn.sparkfun.com/tutorials/what-is-a-circuit
+http://www.allaboutcircuits.com
+References:
+https://www.webassign.net/ebooks/mi4/toc.html?page=23.8
+http://science.howstuffworks.com/environmental/energy/circuit3.htm
+Circuits