Brownian Motion: Difference between revisions
No edit summary |
No edit summary |
||
| (3 intermediate revisions by the same user not shown) | |||
| Line 50: | Line 50: | ||
This proves that existence of osmotic pressure by utilizing from molecular-kinetic theory of Heat. | This proves that existence of osmotic pressure by utilizing from molecular-kinetic theory of Heat. | ||
==Computational Model== | |||
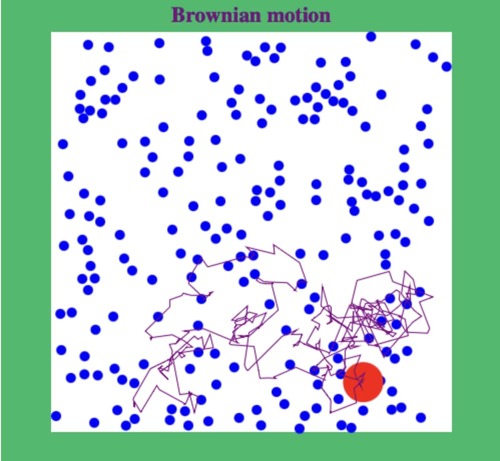
This model depicts Brownian motion, which large particle is in random movement due to collision between particles. Variation in Temperature can also affect the motion of large particle, which indicates this is Temperature-dependent ensemble. Quantitatively, this involves statistical mechanics where you would find the random walk, which is similar to probability. | |||
====At high temperature==== | |||
[[File:HighTmotion123.jpg]] | |||
===At low temperature=== | |||
[[File:LowTmotion123.jpg]] | |||
Link: https://physics.bu.edu/~duffy/HTML5/brownian_motion.html | |||
==Example== | ==Example== | ||
| Line 81: | Line 92: | ||
== References == | == References == | ||
1. **Einstein, A.** (1905). "On the movement of small particles suspended in a stationary liquid." In *Annalen der Physik*. Retrieved from [https://www.mit.edu/~kardar/research/seminars/motility/eins_brownian.pdf](https://www.mit.edu/~kardar/research/seminars/motility/eins_brownian.pdf) | 1. **Einstein, A.** (1905). "On the movement of small particles suspended in a stationary liquid." In *Annalen der Physik*. Retrieved from [https://www.mit.edu/~kardar/research/seminars/motility/eins_brownian.pdf](https://www.mit.edu/~kardar/research/seminars/motility/eins_brownian.pdf) | ||
2. **Brownian Motion**. (n.d.). In *Encyclopaedia Britannica*. Retrieved from [https://www.britannica.com/science/Brownian-motion](https://www.britannica.com/science/Brownian-motion) | 2. **Duffy, D.** (n.d.). *Brownian Motion Simulation*. Retrieved from [https://physics.bu.edu/~duffy/HTML5/brownian_motion.html](https://physics.bu.edu/~duffy/HTML5/brownian_motion.html) | ||
3. **Brownian Motion**. (n.d.). In *Encyclopaedia Britannica*. Retrieved from [https://www.britannica.com/science/Brownian-motion](https://www.britannica.com/science/Brownian-motion) | |||
4. **Brownian Motion**. (n.d.). In *Wikipedia*. Retrieved from [https://en.wikipedia.org/wiki/Brownian_motion](https://en.wikipedia.org/wiki/Brownian_motion) | |||
Latest revision as of 21:47, 6 December 2024
Created by Byun, Jaeyoon on Dec 2024
Foundation of Brownian motion
Brownian motion is the random motion of particles suspended in a medium (a liquid or a gas). It was named for the Scottish botanist Robert Brown, first person to study this motion. It was discovered during investigation of fertilization process in Clarkia pulchella, a flowering plant, as he noticed a "rapid oscillatory motion" of the microscopic particles within the pollen grains suspended in water under the microscope. Initially, he believed it was unusual activity by pollen, but it showed same movement even pollen was dead. Many scientists, such as Albert Einstein, analyzed this strange phenomenon quantitatively.
Theory of Brownian Movement
Osmotic Pressure in Suspended Particles
Consider [math]\displaystyle{ z }[/math] gram of molecules of non-electrolyte dissolve in a volume V* that is part of total volume [math]\displaystyle{ V }[/math]. If volume [math]\displaystyle{ V^* }[/math] is separated from pure solvent by a partition permeable for solvent but not for the solute, "osmotic pressure", [math]\displaystyle{ p }[/math], is exerted on this partition, satisfying the following equation (when [math]\displaystyle{ V^*/z }[/math] is great enough):
[math]\displaystyle{ pV^* = RTz }[/math]
On the other hand, if small suspended particles are present in fractional volume V*, which particles can't pass to the solvent, no force (excluding gravity) will acting on this partition, according to classical Theory of Thermodynamics.
In molecular-kinetic theory of heat, however, provides different conception. According to this theory, a dissolved molecule is differentiated from a suspended body by its dimensions only. So the following assumption is made: suspended particles perform an irregular movement in the liquid on account of the molecular movement of the liquid. If particles are suspended from volume V* by the partition, there will be osmotic pressure p where:
[math]\displaystyle{ p = RTn/NV^* = RTv/N }[/math]
in which v = number of suspended particles present in volume V* and N stands for actual number of molecules.
Osmotic Pressure in Molecular-Kinetic Theory of Heat
If [math]\displaystyle{ p_1, p_2,..., p_i }[/math] are the variables of state of system and if the complete system of equations of change of these variables of state is given as [math]\displaystyle{ \frac{\partial p_v}{\partial t} = \phi_v(p_1...p_2)(v=1,2,...i) }[/math] or [math]\displaystyle{ \sum\frac{\partial \phi_v}{\partial p_v} = 0 }[/math], then the entropy of the system is given as [math]\displaystyle{ S = \frac{\bar{E}}{T} + 2x \log \int \exp\left(-\frac{E}{2xT}\right) dp_1 \cdots dp_i }[/math] where T is absolute temperature, [math]\displaystyle{ E }[/math] is energy of system, and [math]\displaystyle{ \bar{E} }[/math] is the energy as a function of [math]\displaystyle{ p }[/math]. Integration over all possible values, free energy, F, is obtained: [math]\displaystyle{ F = -\frac{RT}{N} \cdot l \cdot g \int \exp\left(-\frac{EN}{RT}\right) dp_1 \cdots dp_i = -\frac{RT}{N} \cdot l \cdot g B }[/math]
Consider, now, a quantity of liquid enclosed in a volume [math]\displaystyle{ V }[/math] with [math]\displaystyle{ n }[/math] solute molecules in [math]\displaystyle{ V^* }[/math] by semi-permeable partition. In order to show that F is depended on the magnitude of the volume [math]\displaystyle{ V^* }[/math] where all suspended particles are contained, variable [math]\displaystyle{ B }[/math] will be incorporated. Let [math]\displaystyle{ x_1, y_1, z_1 }[/math] be the rectangular coordinates system of first particle, [math]\displaystyle{ x_2, y_2, z_2 }[/math] for second particle, and [math]\displaystyle{ x_n, y_n, z_n }[/math] for nth/last particle. Allocating in domains of parallelopiped form [math]\displaystyle{ dx_1, dy_1, dz_1, dx_2, dy_2, dz_2, ...., dx_n, dy_n, dz_n }[/math] within [math]\displaystyle{ V^* }[/math], the function can be written as:
[math]\displaystyle{ dB = dx1dy1...dzn \cdot J }[/math],
in which [math]\displaystyle{ J }[/math] is independent from [math]\displaystyle{ x_1,y_1,z_1,...,z_n }[/math].
If there is a second system of same domain with [math]\displaystyle{ dx_1'dy_1'dz_1', dx_2'dy_2'dz_2',..., dx_n'dy_n'dz_n' }[/math], the function can be written as:
[math]\displaystyle{ dB' = dx_1'dy_1'...dz_n'\cdot J }[/math]
If [math]\displaystyle{ dx_1dy_1...dz_n = dx_1'dy_1'...dz_n' }[/math], then equation becomes:
[math]\displaystyle{ dB/dB' = J/J' }[/math].
Based on this theory, [math]\displaystyle{ dB/B }[/math] or [math]\displaystyle{ dB/B' }[/math] is equal to probability that centers of gravity of particles at specific moment in domains. So, if movement of single particle is independent of one another and is homogenous with no force exerted to particle, probability will be equal, thus [math]\displaystyle{ dB/B = dB'/B' }[/math] which ultimately establishes the equation: [math]\displaystyle{ J = J' }[/math] This proves that J is independent of both [math]\displaystyle{ V^* }[/math] and centres of gravity.
Integrating [math]\displaystyle{ dB }[/math] gives:
[math]\displaystyle{ B = \int J \cdot x_1...dz_n = J \cdot V^* \cdot n }[/math]
Thus, [math]\displaystyle{ F = -\frac{RT}{N} \left( l \cdot g \cdot J + n \cdot l \cdot g \cdot V^* \right) }[/math]
and Osmotic pressure: [math]\displaystyle{ p = \frac{\partial F}{\partial V^*} = \frac{RT}{V^*} \cdot \frac{n}{N} = \frac{RT}{N} \cdot v }[/math]
This proves that existence of osmotic pressure by utilizing from molecular-kinetic theory of Heat.
Computational Model
This model depicts Brownian motion, which large particle is in random movement due to collision between particles. Variation in Temperature can also affect the motion of large particle, which indicates this is Temperature-dependent ensemble. Quantitatively, this involves statistical mechanics where you would find the random walk, which is similar to probability.
At high temperature
At low temperature
Link: https://physics.bu.edu/~duffy/HTML5/brownian_motion.html
Example
Easy:
Estimate the effective radius of a sucrose molecule in water at 25 °C given that its diffusion coefficient is [math]\displaystyle{ 5.2 \times 10^{-10} \, \text{m}^2/\text{s} }[/math] and that the viscosity of water is 1.00 cP
Middling:
T4 is a large bacterial virus. The virus has a symmetric (approximately spherical) head group that contains DNA. These head particles were studied and were found to have the following parameters:
Calculations
Calculate the following:
a. The molecular weight of the head group.
b. The volume in mL of the head group (this assumes no hydration).
c. The frictional coefficient of the head group from the diffusion coefficient.
d. The volume of the head group from the frictional coefficient in part (c) and the Stokes equation.
The difference between the calculated volume in part (b) and the measured volume in part (d) is caused by hydration of the head group.
Hard:
A small molecule with diffusion coefficient [math]\displaystyle{ 2 \, \mu \text{m}^2 \, \text{s}^{-1} }[/math] is initially distributed across a box with a sinusoidal pattern: [math]\displaystyle{ c(x) = \cos(x) + 1 \quad \text{for } 0 \leq x \leq 3.14 \, \text{nm} }[/math]. Obtain an analytical expression for the change in concentration with respect to time throughout the box.
References
1. **Einstein, A.** (1905). "On the movement of small particles suspended in a stationary liquid." In *Annalen der Physik*. Retrieved from [1](https://www.mit.edu/~kardar/research/seminars/motility/eins_brownian.pdf)
2. **Duffy, D.** (n.d.). *Brownian Motion Simulation*. Retrieved from [2](https://physics.bu.edu/~duffy/HTML5/brownian_motion.html)
3. **Brownian Motion**. (n.d.). In *Encyclopaedia Britannica*. Retrieved from [3](https://www.britannica.com/science/Brownian-motion)
4. **Brownian Motion**. (n.d.). In *Wikipedia*. Retrieved from [4](https://en.wikipedia.org/wiki/Brownian_motion)