Temperature: Difference between revisions
No edit summary |
Created a simulation and linked it. |
||
| (17 intermediate revisions by the same user not shown) | |||
| Line 28: | Line 28: | ||
The three Temperature scales are related by the following: | The three Temperature scales are related by the following: | ||
::: | :::\begin{equation}K = 273.15 + °C\end{equation} | ||
:::\begin{equation}C = \left(\frac{5}{9}\right)(°F - 32) \quad \And \quad °C = °K - 273.15\end{equation} | |||
:::\begin{equation}F = \left(\frac{9}{5}\right)(°C) + 32\end{equation} | |||
: | The relationship between Heat transfer and Temperature can be modeled with this equation: | ||
:::< | :::<math>Q = mC\Delta T</math> | ||
In the equation above | |||
<blockquote>''m represents the mass of the system (can be given in Kg or g depending on the units of C)''</blockquote> | |||
<blockquote>''C represents the specific heat capcity of the system(Can given in J·kg⁻¹·K⁻¹ or J·g⁻¹·°C⁻¹)''</blockquote> | |||
<blockquote>''Delta T represents the specific heat capcity of the system(K or °C)''</blockquote> | |||
====Insulated System==== | ====Insulated System==== | ||
| Line 50: | Line 53: | ||
{| border="1" style="text-align:center; margin-left:auto; margin-right:auto" | {| border="1" style="text-align:center; margin-left:auto; margin-right:auto" | ||
|+ | |+ | ||
! Material !! Fractional expansion per <math> | ! Material !! Fractional expansion per <math>°C</math> <math>(10^{-6})</math> !! Fractional expansion per <math>°F \ (10^{-6})</math> | ||
|- | |- | ||
! Glass (Ordinary) | ! Glass (Ordinary) | ||
| Line 103: | Line 106: | ||
===Computational Model=== | ===Computational Model=== | ||
This simulation will show two blocks reaching thermal equilibrium in an insulated system. The blocks have different masses and specific heat capacities. How does this affect the simulation? | |||
<blockquote>'' | |||
# Heat Transfer Simulation in Web VPython (GlowScript) | |||
# Two objects in thermal contact exchanging heat | |||
scene.width = 600 | |||
scene.height = 350 | |||
scene.background = color.white | |||
# -------------------------------------------- | |||
# Parameters | |||
# -------------------------------------------- | |||
m1 = 1.2 # kg | |||
c1 = 3500 # J/(kg C) | |||
T1 = 85 # Celsius (hot object) | |||
m2 = 0.25 # kg | |||
c2 = 2000 # J/(kg C) | |||
T2 = 25 # Celsius (cold object) | |||
k = 15 # thermal coupling constant (arbitrary but reasonable) | |||
dt = 0.05 # timestep | |||
t = 0 | |||
# -------------------------------------------- | |||
# Visual Objects | |||
# -------------------------------------------- | |||
block1 = box(pos=vector(-1,0,0), size=vector(1,1,1), color=color.red) | |||
block2 = box(pos=vector(1,0,0), size=vector(1,1,1), color=color.blue) | |||
label1 = label(pos=block1.pos+vector(0,1.2,0), text=f"T1 = {T1:.2f} °C", height=16, color=color.black) | |||
label2 = label(pos=block2.pos+vector(0,1.2,0), text=f"T2 = {T2:.2f} °C", height=16, color=color.black) | |||
# -------------------------------------------- | |||
# Simulation Loop | |||
# -------------------------------------------- | |||
while abs(T1 - T2) > 0.0001: | |||
rate(60) | |||
# heat flow: Q flows from hotter → colder | |||
dQ = k * (T1 - T2) * dt | |||
# update temperatures based on heat flow | |||
T1 -= dQ / (m1 * c1) | |||
T2 += dQ / (m2 * c2) | |||
# update graphics | |||
label1.text = f"T1 = {T1:.2f} °C" | |||
label2.text = f"T2 = {T2:.2f} °C" | |||
# colors fade toward equilibrium | |||
mix = (T1 - T2) / 100 | |||
block1.color = vector(1, 0, 0) * (1 - mix) | |||
block2.color = vector(0, 0, 1) * (1 + mix) | |||
t += dt | |||
print("Thermal equilibrium reached:") | |||
print(f"Final temperature = {T1:.3f} °C") | |||
''</blockquote> | |||
https://trinket.io/embed/glowscript/4ec4f3e21fc4?start=result | |||
==Examples== | ==Examples== | ||
| Line 112: | Line 178: | ||
{| class="wikitable" style="text-align:center; margin-left:auto; margin-right:auto; width:5; length:5" | {| class="wikitable" style="text-align:center; margin-left:auto; margin-right:auto; width:5; length:5" | ||
|- | |- | ||
! Fahrenheit <math>( | ! Fahrenheit <math>(°F)</math> | ||
! Celsius <math>( | ! Celsius <math>(°C)</math> | ||
! Kelvin <math>( | ! Kelvin <math>(K)</math> | ||
|- | |- | ||
| <math>142</math> | | <math>142</math> | ||
| Line 131: | Line 197: | ||
:''Row 1:'' | :''Row 1:'' | ||
::<math> | ::<math>142°F: °C = \left(\frac{5}{9}\right)(142 - 32) = \left(\frac{5}{9}\right)(110) \approx 61.11°C</math> | ||
::<math>61. | ::<math>61.11°C: K = 273.15 + °C \approx 273.15 + 61.11 = 334.26K</math> | ||
:''Row 2:'' | :''Row 2:'' | ||
::<math> | ::<math>31K: °C = K - 273.15 = 31 - 273.15 = -242.15°C</math> | ||
::<math>-242. | ::<math>-242.12°C: °F = \left(\frac{9}{5}\right)(°C + 32) = \left(\frac{9}{5}\right)(-241.15 + 32) = \left(\frac{9}{5}\right)(-210.15) = -116.75°F</math> | ||
:''Row 3:'' | :''Row 3:'' | ||
::<math> | ::<math>350°C: °F = \left(\frac{9}{5}\right)(°C + 32) = \left(\frac{9}{5}\right)(350 + 32) = \left(\frac{9}{5}\right)(382) = 687.2°F</math> | ||
::<math> | ::<math>350°C: K = 273.15 + °C = 273.15 + 350 = 623.15K</math> | ||
:Now, we can fill in the table: | :Now, we can fill in the table: | ||
| Line 151: | Line 217: | ||
{| class="wikitable" style="text-align:center; margin-left:auto; margin-right:auto; width:5; length:5" | {| class="wikitable" style="text-align:center; margin-left:auto; margin-right:auto; width:5; length:5" | ||
|- | |- | ||
! Fahrenheit <math>( | ! Fahrenheit <math>(°F)</math> | ||
! Celsius <math>( | ! Celsius <math>(°C)</math> | ||
! Kelvin <math>( | ! Kelvin <math>(K)</math> | ||
|- | |- | ||
| <math>142</math> | | <math>142</math> | ||
| Line 169: | Line 235: | ||
===Middling=== | ===Middling=== | ||
On Thanksgiving morning, your mom cooked a turkey with a mass of <math>m = 12.55 \ kg</math>. It had a Temperature of <math> | On Thanksgiving morning, your mom cooked a turkey with a mass of <math>m = 12.55 \ kg</math>. It had a Temperature of <math>85°C</math> coming out of the oven. By the time everyone is seated at the table and ready to eat the turkey, its Temperature is now <math>43°C</math>. The specific heat for the turkey is <math>5.16 \left(\frac{J}{g \cdot C}\right)</math>. | ||
:'''a) Determine the Heat lost by the turkey.''' | :'''a) Determine the Heat lost by the turkey.''' | ||
| Line 186: | Line 252: | ||
===Difficult=== | ===Difficult=== | ||
You take a slice of the turkey. This slice has a mass of <math>m_{slice} = 1.12 \ kg</math>. The Temperature of it is <math>85°F</math>. You also place some sauce on top of it. The sauce has a mass of <math> m_{sauce} = 0.044 \ kg</math>, an initial temperature <math>T_{sauce_{0}} = | You take a slice of the turkey. This slice has a mass of <math>m_{slice} = 1.12 \ kg</math>. The Temperature of it is <math>85°F</math>. You also place some sauce on top of it. The sauce has a mass of <math> m_{sauce} = 0.044 \ kg</math>, an initial temperature <math>T_{sauce_{0}} = 65°F</math> , and a specific heat of <math>C_{sauce} = 2.2 \ \left(\frac{J}{g \cdot C}\right)</math>. | ||
'''a) Assuming the slice of turkey and the sauce are an isolated system, what is the final Temperature reached in Thermodynamic Equilibrium?''' | '''a) Assuming the slice of turkey and the sauce are an isolated system, what is the final Temperature reached in Thermodynamic Equilibrium?''' | ||
| Line 213: | Line 279: | ||
::Now, we need to convert the Fahrenheit Temperatures to Celsius and kilograms to grams: | ::Now, we need to convert the Fahrenheit Temperatures to Celsius and kilograms to grams: | ||
:::<math>T_{slice_{0}}( | :::<math>T_{slice_{0}}(°C) = \left(\frac{5}{9}\right)(T_{slice_{0}}(°F) - 32) = \left(\frac{5}{9}\right)(85 - 32) = \left(\frac{5}{9}\right)(53) \approx 29.44°C</math> | ||
:::<math>T_{sauce_{0}}( | :::<math>T_{sauce_{0}}(°C) = \left(\frac{5}{9}\right)(T_{sauce_{0}}(°F - 32) = \left(\frac{5}{9}\right)(65 - 32) = \left(\frac{5}{9}\right)(33) \approx 18.33°C</math> | ||
:::<math>m_{slice}: 1.12 \ (kg) \times \frac{1,000}{1} \left(\frac{g}{kg}\right) = 1,120 \ g</math> | :::<math>m_{slice}: 1.12 \ (kg) \times \frac{1,000}{1} \left(\frac{g}{kg}\right) = 1,120 \ g</math> | ||
| Line 223: | Line 289: | ||
::We can calculate the final Temperature of the system now: | ::We can calculate the final Temperature of the system now: | ||
:::<math>T_{f} = \frac{(1,120 \times 5.16 \times 29.44) + (44 \times 2.2 \times 18.33)}{(1,120 \times 5.16) + (44 \times 2.2)} = \frac{(170,139.648) + (1,774.344)}{(5,779.2) + (96.8)} = \frac{171,913.992}{5,876} = 29. | :::<math>T_{f} = \frac{(1,120 \times 5.16 \times 29.44) + (44 \times 2.2 \times 18.33)}{(1,120 \times 5.16) + (44 \times 2.2)} = \frac{(170,139.648) + (1,774.344)}{(5,779.2) + (96.8)} = \frac{171,913.992}{5,876} = 29.257°C</math> | ||
==Connectedness== | ==Connectedness== | ||
Latest revision as of 18:11, 2 December 2025
Main Idea
EDITED BY MASON FOSDICK FALL25
Temperature is the measure of the Average Kinetic Energy of the particles in a system. The difference between Temperature, Thermal Energy, and Heat is:
Thermal Energy is the sum of all the kinetic energies of the particles in a system
Heat is the transfer of Thermal Energy
Applying Heat to a system usually causes its Temperature to rise; the loss of Heat by a system typically corresponds to decrease in Temperature. The Zeroth Law of Thermodynamics states:
If system A is in Thermodynamic Equilibrium with system B, and if system B is in Thermodynamic Equilibrium with system C, then system A is also in Thermodynamic Equilibrium with system C
Thermodynamic Equilibrium is defined as:
A state in which a system's macroscopic properties (temperature, pressure, etc.) do not change dependent on time and there are no net flows of energy or matter within the system. When two systems are in thermal contact and equilibrium, there is not net heat flow between them.
Thus, a system's Temperature is the same throughout when it is in Thermodynamic Equilibrium.
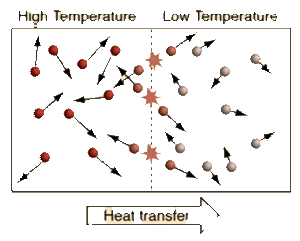
We see from the definition of Thermodynamic Equilibrium and The Zeroth Law of Thermodynamics that a Temperature difference is needed for Heat to flow from a warmer Temperature system to a cooler Temperature system. When systems with different Temperatures are in contact, the molecules in the system with higher average kinetic energy collide with the molecules of the system with lower average kinetic energy; kinetic energy is passed from the molecules with more kinetic energy to those with less kinetic energy. This molecular level of kinetic energy transfer will happen until the average kinetic energy of the particles in each system reaches the weighted average of the two systems. This idea can be applied to a multi-system interaction as well.
Mathematical Model
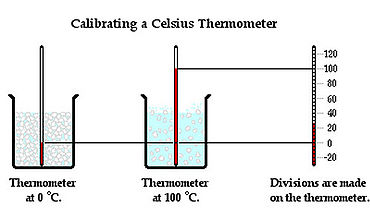
A thermometer is a device used to measure the Temperature of a system. It is placed in contact with an object and allowed to reach Thermal Equilibrium with the object, and thus the same Temperature. The operation of a thermometer is based on some property, such as volume, that varies with Temperature. For example, mercury in a mercury thermometer expands to a degree depending on a temperature of the object and the level of the mercury inside the glass tube rises or descends due to this.
Temperature can be measured in numbers by three Temperature scales: Celsius, Fahrenheit, and Kelvin. The Celsius scale sets the freezing point of the water at 0 degrees and the boiling point of water at 100 degrees. The Fahrenheit scale sets the freezing point of water at 32 degrees and the boiling point of the water at 212 degrees. The Kelvin scale is designed to go to 0 at absolute zero, the minimum possible temperature in the Universe.
The three Temperature scales are related by the following:
- \begin{equation}K = 273.15 + °C\end{equation}
- \begin{equation}C = \left(\frac{5}{9}\right)(°F - 32) \quad \And \quad °C = °K - 273.15\end{equation}
- \begin{equation}F = \left(\frac{9}{5}\right)(°C) + 32\end{equation}
The relationship between Heat transfer and Temperature can be modeled with this equation:
- [math]\displaystyle{ Q = mC\Delta T }[/math]
In the equation above
m represents the mass of the system (can be given in Kg or g depending on the units of C)
C represents the specific heat capcity of the system(Can given in J·kg⁻¹·K⁻¹ or J·g⁻¹·°C⁻¹)
Delta T represents the specific heat capcity of the system(K or °C)
Insulated System
An insulated system occurs when there is no transfer of heat between the system and the surroundings. Q=0
Thermal Expansion
A change in the Temperature of a body through Heat transfer can change the shape, area, and volume of the body. When a substance is heated, the kinetic energy of its molecules increases. Then, the molecules begin moving more and more, and the average separation between molecules become larger, and thus the volume of the body changes. The degree of expansion divided by the change in Temperature is called the material's Coefficient of Thermal Expansion and generally varies with Temperature, the object, and state of matter of the object.
| Material | Fractional expansion per [math]\displaystyle{ °C }[/math] [math]\displaystyle{ (10^{-6}) }[/math] | Fractional expansion per [math]\displaystyle{ °F \ (10^{-6}) }[/math] |
|---|---|---|
| Glass (Ordinary) | [math]\displaystyle{ 9 }[/math] | [math]\displaystyle{ 5 }[/math] |
| Glass (Pyrex) | [math]\displaystyle{ 4 }[/math] | [math]\displaystyle{ 2.2 }[/math] |
| Quartz (Fused) | [math]\displaystyle{ 0.59 }[/math] | [math]\displaystyle{ 0.33 }[/math] |
| Aluminum | [math]\displaystyle{ 24 }[/math] | [math]\displaystyle{ 13 }[/math] |
| Brass | [math]\displaystyle{ 19 }[/math] | [math]\displaystyle{ 11 }[/math] |
| Copper | [math]\displaystyle{ 17 }[/math] | [math]\displaystyle{ 9.4 }[/math] |
| Iron | [math]\displaystyle{ 12 }[/math] | [math]\displaystyle{ 6.7 }[/math] |
| Steel | [math]\displaystyle{ 13 }[/math] | [math]\displaystyle{ 7.2 }[/math] |
| Platinum | [math]\displaystyle{ 9 }[/math] | [math]\displaystyle{ 5 }[/math] |
| Tungsten | [math]\displaystyle{ 4.3 }[/math] | [math]\displaystyle{ 2.4 }[/math] |
| Gold | [math]\displaystyle{ 14 }[/math] | [math]\displaystyle{ 7.8 }[/math] |
| Silver | [math]\displaystyle{ 18 }[/math] | [math]\displaystyle{ 10 }[/math] |
Computational Model
This simulation will show two blocks reaching thermal equilibrium in an insulated system. The blocks have different masses and specific heat capacities. How does this affect the simulation?
- Heat Transfer Simulation in Web VPython (GlowScript)
- Two objects in thermal contact exchanging heat
scene.width = 600 scene.height = 350 scene.background = color.white
- --------------------------------------------
- Parameters
- --------------------------------------------
m1 = 1.2 # kg c1 = 3500 # J/(kg C) T1 = 85 # Celsius (hot object)
m2 = 0.25 # kg c2 = 2000 # J/(kg C) T2 = 25 # Celsius (cold object)
k = 15 # thermal coupling constant (arbitrary but reasonable) dt = 0.05 # timestep t = 0
- --------------------------------------------
- Visual Objects
- --------------------------------------------
block1 = box(pos=vector(-1,0,0), size=vector(1,1,1), color=color.red) block2 = box(pos=vector(1,0,0), size=vector(1,1,1), color=color.blue)
label1 = label(pos=block1.pos+vector(0,1.2,0), text=f"T1 = {T1:.2f} °C", height=16, color=color.black) label2 = label(pos=block2.pos+vector(0,1.2,0), text=f"T2 = {T2:.2f} °C", height=16, color=color.black)
- --------------------------------------------
- Simulation Loop
- --------------------------------------------
while abs(T1 - T2) > 0.0001: rate(60)
# heat flow: Q flows from hotter → colder dQ = k * (T1 - T2) * dt
# update temperatures based on heat flow T1 -= dQ / (m1 * c1) T2 += dQ / (m2 * c2)
# update graphics label1.text = f"T1 = {T1:.2f} °C" label2.text = f"T2 = {T2:.2f} °C"
# colors fade toward equilibrium mix = (T1 - T2) / 100 block1.color = vector(1, 0, 0) * (1 - mix) block2.color = vector(0, 0, 1) * (1 + mix)
t += dt
print("Thermal equilibrium reached:") print(f"Final temperature = {T1:.3f} °C")
https://trinket.io/embed/glowscript/4ec4f3e21fc4?start=result
Examples
Simple
Complete the following Temperature table:
| Fahrenheit [math]\displaystyle{ (°F) }[/math] | Celsius [math]\displaystyle{ (°C) }[/math] | Kelvin [math]\displaystyle{ (K) }[/math] |
|---|---|---|
| [math]\displaystyle{ 142 }[/math] | ? | ? |
| ? | ? | [math]\displaystyle{ 31 }[/math] |
| ? | [math]\displaystyle{ 350 }[/math] | ? |
- Row 1:
- [math]\displaystyle{ 142°F: °C = \left(\frac{5}{9}\right)(142 - 32) = \left(\frac{5}{9}\right)(110) \approx 61.11°C }[/math]
- [math]\displaystyle{ 61.11°C: K = 273.15 + °C \approx 273.15 + 61.11 = 334.26K }[/math]
- Row 2:
- [math]\displaystyle{ 31K: °C = K - 273.15 = 31 - 273.15 = -242.15°C }[/math]
- [math]\displaystyle{ -242.12°C: °F = \left(\frac{9}{5}\right)(°C + 32) = \left(\frac{9}{5}\right)(-241.15 + 32) = \left(\frac{9}{5}\right)(-210.15) = -116.75°F }[/math]
- Row 3:
- [math]\displaystyle{ 350°C: °F = \left(\frac{9}{5}\right)(°C + 32) = \left(\frac{9}{5}\right)(350 + 32) = \left(\frac{9}{5}\right)(382) = 687.2°F }[/math]
- [math]\displaystyle{ 350°C: K = 273.15 + °C = 273.15 + 350 = 623.15K }[/math]
- Now, we can fill in the table:
| Fahrenheit [math]\displaystyle{ (°F) }[/math] | Celsius [math]\displaystyle{ (°C) }[/math] | Kelvin [math]\displaystyle{ (K) }[/math] |
|---|---|---|
| [math]\displaystyle{ 142 }[/math] | [math]\displaystyle{ 61.11 }[/math] | [math]\displaystyle{ 334.26 }[/math] |
| [math]\displaystyle{ -116.75 }[/math] | [math]\displaystyle{ -242.15 }[/math] | [math]\displaystyle{ 31 }[/math] |
| [math]\displaystyle{ 687.2 }[/math] | [math]\displaystyle{ 350 }[/math] | [math]\displaystyle{ 623.15 }[/math] |
Middling
On Thanksgiving morning, your mom cooked a turkey with a mass of [math]\displaystyle{ m = 12.55 \ kg }[/math]. It had a Temperature of [math]\displaystyle{ 85°C }[/math] coming out of the oven. By the time everyone is seated at the table and ready to eat the turkey, its Temperature is now [math]\displaystyle{ 43°C }[/math]. The specific heat for the turkey is [math]\displaystyle{ 5.16 \left(\frac{J}{g \cdot C}\right) }[/math].
- a) Determine the Heat lost by the turkey.
- We can use this equation to relate the Heat loss to the Temperature change:
- [math]\displaystyle{ \Delta Q = mC \Delta T }[/math]
- First, we will convert the mass of the turkey to grams:
- [math]\displaystyle{ m_{kg} = 12.55 \ kg \quad \And \quad 1 \ kg = 1,000 \ g \quad \therefore \quad m_{g} = 12.55 \ (kg) \times \frac{1,000}{1} \ \left(\frac{g}{kg}\right) = 12,550 \ g }[/math]
- Now, we can calculate the change in Thermal Energy of the turkey:
- [math]\displaystyle{ \Delta Q = m_{g} C \Delta T_{turkey} = 12,550 \times 5.16 \times (43 - 85) = -2,719,836 \ J }[/math]
Difficult
You take a slice of the turkey. This slice has a mass of [math]\displaystyle{ m_{slice} = 1.12 \ kg }[/math]. The Temperature of it is [math]\displaystyle{ 85°F }[/math]. You also place some sauce on top of it. The sauce has a mass of [math]\displaystyle{ m_{sauce} = 0.044 \ kg }[/math], an initial temperature [math]\displaystyle{ T_{sauce_{0}} = 65°F }[/math] , and a specific heat of [math]\displaystyle{ C_{sauce} = 2.2 \ \left(\frac{J}{g \cdot C}\right) }[/math].
a) Assuming the slice of turkey and the sauce are an isolated system, what is the final Temperature reached in Thermodynamic Equilibrium?
- Within an isolated system, energy must be conserved. Also, the only kind of change in energy is through Heat; no Work is being done. The Thermal Energy of the slice of turkey will warm the sauce.
- Thus, we can use the Energy Principle to describe the scenario:
- [math]\displaystyle{ \Delta E_{system} = Q + W = 0\quad \And \quad W = 0 }[/math]
- [math]\displaystyle{ \Delta E_{system} = Q = 0 }[/math]
- This change in energy of the system is a change in Thermal Energy:
- [math]\displaystyle{ \Delta Q_{system} = Q = 0 \quad \And \quad \Delta Q = mC \Delta T }[/math]
- [math]\displaystyle{ \Delta Q_{system} = \Delta Q_{slice} + \Delta Q_{sauce} = 0 }[/math]
- [math]\displaystyle{ \Delta Q_{slice} + \Delta Q_{sauce} = m_{slice}C_{turkey} \Delta T_{slice} + m_{sauce}C_{sauce} \Delta T_{sauce} = 0 }[/math]
- [math]\displaystyle{ m_{slice}C_{turkey} \Delta T_{slice} + m_{sauce}C_{sauce} \Delta T_{sauce} = m_{slice}C_{turkey}(T_{f} - T_{slice_{0}}) + m_{sauce}C_{sauce}(T_{f} - T_{sauce_{0}}) = 0 }[/math]
- [math]\displaystyle{ (m_{slice}C_{turkey} + m_{sauce}C_{sauce}) T_{f} = m_{slice}C_{turkey}T_{slice_{0}} + m_{sauce}C_{sauce}T_{sauce_{0}} }[/math]
- [math]\displaystyle{ T_{f} = \frac{m_{slice}C_{turkey}T_{slice_{0}} + m_{sauce}C_{sauce}T_{sauce_{0}}}{m_{slice}C_{turkey} + m_{sauce}C_{sauce}} }[/math]
- Now, we need to convert the Fahrenheit Temperatures to Celsius and kilograms to grams:
- [math]\displaystyle{ T_{slice_{0}}(°C) = \left(\frac{5}{9}\right)(T_{slice_{0}}(°F) - 32) = \left(\frac{5}{9}\right)(85 - 32) = \left(\frac{5}{9}\right)(53) \approx 29.44°C }[/math]
- [math]\displaystyle{ T_{sauce_{0}}(°C) = \left(\frac{5}{9}\right)(T_{sauce_{0}}(°F - 32) = \left(\frac{5}{9}\right)(65 - 32) = \left(\frac{5}{9}\right)(33) \approx 18.33°C }[/math]
- [math]\displaystyle{ m_{slice}: 1.12 \ (kg) \times \frac{1,000}{1} \left(\frac{g}{kg}\right) = 1,120 \ g }[/math]
- [math]\displaystyle{ m_{sauce}: 0.044 \ (kg) \times \frac{1,000}{1} \left(\frac{g}{kg}\right) = 44 \ g }[/math]
- We can calculate the final Temperature of the system now:
- [math]\displaystyle{ T_{f} = \frac{(1,120 \times 5.16 \times 29.44) + (44 \times 2.2 \times 18.33)}{(1,120 \times 5.16) + (44 \times 2.2)} = \frac{(170,139.648) + (1,774.344)}{(5,779.2) + (96.8)} = \frac{171,913.992}{5,876} = 29.257°C }[/math]
Connectedness
The idea of Temperature is integral to life. Every morning, millions of people will check the weather for two reasons; to check the Temperature and see if rain is in the forecast. We set the Temperature on our ovens daily, select a Temperature on our thermostats, and millions of people will check the weather for two reasons; to check the Temperature and see if rain is in the forecast. Temperature's effects on life are extensive. Thus, a thoughtful study of these effects and Temperature is very useful to improve everyday life.
History
Early explanations of Heat were thoroughly confused with explanations of combustion. J. J. Becher and George Ernst Stahl introduced the Phlogiston Theory of Combustion in the 17th century, and Phlogiston was thought to be the substance of Heat.
In late 18th century, Antoine Lavoisier argued that Phlogiston Theory is inconsistent, and introduced Caloric Theory. The suggested explanation was that when an object was heated, an invisible fluid called “caloric” was added to the object. Hot objects contained more caloric than cold objects. Caloric theory was popularly accepted until the mid 19th century.
Followed by introduction of Caloric Theory, Count Rumford found that boring a cannon repeatedly does not result in Heat producing ability, and therefore caloric is not lost. This proposed that caloric might not be a substance, though the experimental ambiguity in this experiment was widely considered controversial.
In the mid 19th century, Rudolf Clausius showed that Rumford's argument and Caloric Theory can be agreeable if the Caloric Theory included the principle of conservation of energy in place of its original principle of conservation of Heat. By doing so, the Caloric Theory was able to be evolved into modern Thermodynamics where Heat is described as the transfer of Thermal Energy, which is equivalent to the kinetic energy of the particles of a substance.
See also
Further reading
- http://hyperphysics.phy-astr.gsu.edu/hbase/tables/thexp.html
- http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/temper.html
- http://teachers.oregon.k12.wi.us/mahr/assignments/thermal_energyvs_temp.pdf
External links
- https://en.wikipedia.org/wiki/Thermal_equilibrium
- http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/thereq.html
- https://phys.libretexts.org/Bookshelves/University_Physics/Book%3A_University_Physics_(OpenStax)/Map%3A_University_Physics_II_-_Thermodynamics%2C_Electricity%2C_and_Magnetism_(OpenStax)/1%3A_Temperature_and_Heat/1.1%3A_Temperature_and_Thermal_Equilibrium
- https://en.wikipedia.org/wiki/Zeroth_law_of_thermodynamics