Energy Density and Electric Field: Difference between revisions
Snileshwar3 (talk | contribs) No edit summary |
Snileshwar3 (talk | contribs) No edit summary |
||
| (22 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
== Mathematical Model == | |||
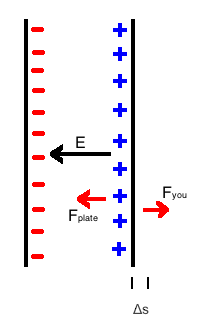
[[File:capacitorPHYSLIFE.png|thumb|right|]]This section takes an alternative view and treats electric fields as if they have energy stored in them. To learn how this works, consider moving one plate of a capacitor. For a very small gap, the force of one capacitor plate on another capacitor plate is charge Q times the field made by the other plate: | |||
== | |||
This section takes an alternative view and treats electric fields as if they have energy stored in them. To learn how this works, consider moving one plate of a capacitor. For a very small gap, the force of one capacitor plate on another capacitor plate is charge Q times the field made by the other plate: | |||
<math>E_{one plate}=\frac{(Q/A)}{2\epsilon_0 } </math> | <math>E_{one plate}=\frac{(Q/A)}{2\epsilon_0 } </math> | ||
Then the force on one plate is: | Then the force on one plate is: | ||
<math>F=Q\frac{(Q/A)}{2\epsilon_0} </math> | <math>F=Q\frac{(Q/A)}{2\epsilon_0} </math> | ||
Now, suppose that you pull the positive plate of the capacitor slowly away from the negative plate, exerting a force that is just barely larger than the one exerted by the other plate. This work that you do, moving the plate a distance Δs, increases the potential energy: | Now, suppose that you pull the positive plate of the capacitor slowly away from the negative plate, exerting a force that is just barely larger than the one exerted by the other plate. This work that you do, moving the plate a distance Δs, increases the potential energy: | ||
<math>ΔU=W=Q\frac{(Q/A)}{2\epsilon_0}Δs</math> | <math>ΔU=W=Q\frac{(Q/A)}{2\epsilon_0}Δs</math> | ||
For the sake of simplification, working out the math, we get this representation: | For the sake of simplification, working out the math, we get this representation: | ||
<math>ΔU=\frac{1}{2}\epsilon_0{(\frac{Q/A}{\epsilon_0})^2}AΔs </math> | |||
The expression in parenthesis that we are squaring is the same as the electric field inside the capacitor. Substituting, we get: | |||
'''Field Energy Density'''= | |||
<math>\frac{ΔU}{Δ(volume)}=\frac{1}{2}\epsilon_0E^2 </math> | |||
The units of Field Energy Density are <math>J/m^3 </math>. | |||
Keep in mind the above equation is solved for the electric field from a capacitor. You can actually use anything with an electric field to derive this above equation. | |||
==Examples== | |||
===Simple=== | |||
Problem: What is the energy density of an electric field of magnitude 600V/m? | |||
Solution: Simply, plug in the electric field into the equation: <math>\frac{1}{2}\epsilon_0E^2 </math> and you will get <math>1.59*10^{-6} J/m^3</math> | |||
===Middling=== | |||
Problem: What is the energy density a distance of 1 cm away on the axis of the positive end a dipole? (s=.1mm, q=4nC) | |||
Solution: | |||
Step 1: First, you must solve for the magnitude of the electric field 1 cm away from the dipole. Use the equation for the E field of a dipole on the axis: <math>E=\frac{1}{4\pi\epsilon_0}\frac{2qs}{r^3} </math> Plugging in, we get E=72 V/m. | |||
Step 2: Then we plug the value for E into the energy density equation: <math>\frac{1}{2}\epsilon_0E^2 </math>. The answer is <math> 2.26*10^{-8} J/m^3</math> | |||
===Difficult=== | |||
An example of a difficult problem would be proving the energy density equation, like we did above. And then applying it like we did in the middling example. This type of combination for a problem would be one that may appear on your test or lab quiz. | |||
==Connectedness== | |||
This topic is connected with energy and electric fields. It puts together those two concepts, rather large concepts and shows how the two of them are related to each other. It's a very subtle, but very necessary relationship that interconnects two large concepts. An example of putting this concept to use would be perhaps finding the energy density of a battery that gives off a electric field. This would be key when working with all types of electronics that require batteries. | |||
==History== | |||
Electric Fields, as we know, were first studied by Coulomb in the late 1700s in France. As individuals studied deeper into the concept, the relationship between energy density and the electric field was derived. Help from Richard Feynman was necessary in connecting the two. | |||
==See Also== | |||
1. https://en.wikipedia.org/wiki/Energy_density#Energy_density_of_electric_and_magnetic_fields | |||
2. http://web.mit.edu/viz/EM/visualizations/coursenotes/modules/guide05.pdf | |||
==Further Reading== | |||
http://www.bearsoft.co.uk/StatE.html | |||
==References== | |||
1. Matter and Interactions, 4th Ed., Chabay and Sherwood. | |||
2. http://www.bearsoft.co.uk/StatE.html | |||
3. http://web.mit.edu/viz/EM/visualizations/coursenotes/modules/guide05.pdf | |||
4. https://en.wikipedia.org/wiki/Energy_density#Energy_density_of_electric_and_magnetic_fields | |||
Page created by Snileshwar3 | |||
Latest revision as of 22:51, 30 November 2015
Mathematical Model
This section takes an alternative view and treats electric fields as if they have energy stored in them. To learn how this works, consider moving one plate of a capacitor. For a very small gap, the force of one capacitor plate on another capacitor plate is charge Q times the field made by the other plate:
[math]\displaystyle{ E_{one plate}=\frac{(Q/A)}{2\epsilon_0 } }[/math]
Then the force on one plate is: [math]\displaystyle{ F=Q\frac{(Q/A)}{2\epsilon_0} }[/math]
Now, suppose that you pull the positive plate of the capacitor slowly away from the negative plate, exerting a force that is just barely larger than the one exerted by the other plate. This work that you do, moving the plate a distance Δs, increases the potential energy: [math]\displaystyle{ ΔU=W=Q\frac{(Q/A)}{2\epsilon_0}Δs }[/math]
For the sake of simplification, working out the math, we get this representation: [math]\displaystyle{ ΔU=\frac{1}{2}\epsilon_0{(\frac{Q/A}{\epsilon_0})^2}AΔs }[/math]
The expression in parenthesis that we are squaring is the same as the electric field inside the capacitor. Substituting, we get:
Field Energy Density= [math]\displaystyle{ \frac{ΔU}{Δ(volume)}=\frac{1}{2}\epsilon_0E^2 }[/math]
The units of Field Energy Density are [math]\displaystyle{ J/m^3 }[/math].
Keep in mind the above equation is solved for the electric field from a capacitor. You can actually use anything with an electric field to derive this above equation.
Examples
Simple
Problem: What is the energy density of an electric field of magnitude 600V/m?
Solution: Simply, plug in the electric field into the equation: [math]\displaystyle{ \frac{1}{2}\epsilon_0E^2 }[/math] and you will get [math]\displaystyle{ 1.59*10^{-6} J/m^3 }[/math]
Middling
Problem: What is the energy density a distance of 1 cm away on the axis of the positive end a dipole? (s=.1mm, q=4nC)
Solution:
Step 1: First, you must solve for the magnitude of the electric field 1 cm away from the dipole. Use the equation for the E field of a dipole on the axis: [math]\displaystyle{ E=\frac{1}{4\pi\epsilon_0}\frac{2qs}{r^3} }[/math] Plugging in, we get E=72 V/m.
Step 2: Then we plug the value for E into the energy density equation: [math]\displaystyle{ \frac{1}{2}\epsilon_0E^2 }[/math]. The answer is [math]\displaystyle{ 2.26*10^{-8} J/m^3 }[/math]
Difficult
An example of a difficult problem would be proving the energy density equation, like we did above. And then applying it like we did in the middling example. This type of combination for a problem would be one that may appear on your test or lab quiz.
Connectedness
This topic is connected with energy and electric fields. It puts together those two concepts, rather large concepts and shows how the two of them are related to each other. It's a very subtle, but very necessary relationship that interconnects two large concepts. An example of putting this concept to use would be perhaps finding the energy density of a battery that gives off a electric field. This would be key when working with all types of electronics that require batteries.
History
Electric Fields, as we know, were first studied by Coulomb in the late 1700s in France. As individuals studied deeper into the concept, the relationship between energy density and the electric field was derived. Help from Richard Feynman was necessary in connecting the two.
See Also
1. https://en.wikipedia.org/wiki/Energy_density#Energy_density_of_electric_and_magnetic_fields
2. http://web.mit.edu/viz/EM/visualizations/coursenotes/modules/guide05.pdf
Further Reading
http://www.bearsoft.co.uk/StatE.html
References
1. Matter and Interactions, 4th Ed., Chabay and Sherwood.
2. http://www.bearsoft.co.uk/StatE.html
3. http://web.mit.edu/viz/EM/visualizations/coursenotes/modules/guide05.pdf
4. https://en.wikipedia.org/wiki/Energy_density#Energy_density_of_electric_and_magnetic_fields
Page created by Snileshwar3