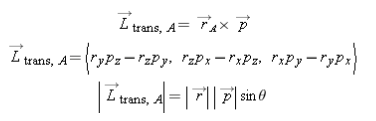The Angular Momentum Principle: Difference between revisions
| (28 intermediate revisions by the same user not shown) | |||
| Line 11: | Line 11: | ||
Total angular momentum is equal to the sum of translational angular momentum about location A and rotational angular momentum about the object's center of mass. In multi-particle systems, the translational angular momentum is equal to the vector product of the distance of the center of mass to location A and total momentum of the whole system. Rotational angular momentum is equal to the vector product of the distance of particle 1 to center of mass and momentum of particle 1 plus the vector product of distance of particle 2 to center of mass and momentum of particle 2 plus all the particles in the system. If total angular momentum and translational angular momentum are known then rotational angular momentum can be found just by subtracting Ltrans from Ltot and if Ltot and Lrot are known, Ltrans can be found by subtracting Lrot from Ltot. | Total angular momentum is equal to the sum of translational angular momentum about location A and rotational angular momentum about the object's center of mass. In multi-particle systems, the translational angular momentum is equal to the vector product of the distance of the center of mass to location A and total momentum of the whole system. Rotational angular momentum is equal to the vector product of the distance of particle 1 to center of mass and momentum of particle 1 plus the vector product of distance of particle 2 to center of mass and momentum of particle 2 plus all the particles in the system. If total angular momentum and translational angular momentum are known then rotational angular momentum can be found just by subtracting Ltrans from Ltot and if Ltot and Lrot are known, Ltrans can be found by subtracting Lrot from Ltot. | ||
[[File:conservationofmomentum.png]] | |||
The total angular momentum of the system plus the total angular momentum of the surroundings is equal to zero and this is called the conservation of angular momentum. Angular momentum is conserved so if system gains angular momentum, the surroundings lose that amount. | |||
[[File:am4.png]] | |||
The derivative of total angular momentum is equal to the torque around location A. | |||
[[File:am3.png]] | [[File:am3.png]] | ||
[[File: | Torque is equal to the vector product of the distance from location A to the point of the application of the force and the force itself. | ||
[[File:torque1.png]] | |||
Torque can also be found by multiplying the magnitude of the direction vector from location A to the point of application of the force, the magnitude of the force applied and sin of theta. Theta is the angle the two vectors make when they are put tail to tail. | |||
[[File:am5.png]] | [[File:am5.png]] | ||
The angular momentum principle states that the change in total angular momentum in a system is equal to the torque applied to the system times the time the torque is applied. If there is no force acting on the system then there is no torque acting on the system so change in total angular momentum of the system is equal to zero. | |||
[[File:amprinciple.png]] | [[File:amprinciple.png]] | ||
Another way of writing the angular momentum principle is the final total angular momentum is equal to the initial total angular momentum plus the angular impulse. This is true because the change in total angular momentum is equal to final total angular momentum minus initial total angular momentum and you can add initial total angular momentum to the other side of the equation to get this equation. Once again, if there is no force acting on the system then there is no torque acting on the system and the angular impulse is equal to zero so final total angular momentum equals initial total angular momentum. | |||
For more information- https://www.youtube.com/watch?v=k9IFb3g2e2M | |||
== A Computational Model == | == A Computational Model == | ||
[[File:angularmomentumpython.png]] | |||
This vPython code shows how to solve for final total angular momentum of an object (in this case a comet orbiting around the Sun) using the angular momentum principle to update total angular momentum over the course of a certain amount of time. Initial constants were defined- such as the position of the Sun and comet, radii of the Sun and comet, mass of the Sun and comet, initial velocity of the comet, inertia of the comet (inertia for a sphere is equal to 2/5 times the mass of the comet times the radius of the comet squared), angular velocity of the comet about its own axis, force applied to the comet, and G (the gravitational constant). In the while loop, the momentum of the comet is found and the gravitational force of the Sun on the comet is found to update the position of the comet as it orbits the Sun. Next, translational momentum of the comet around the Sun is found by the cross product of the momentum of the comet and r (which is the distance from the comet to the Sun). Rotational angular momentum is found by multiplyng the inertia of the comet with the angular velocity of the comet. Total angular momentum is the sum of Lrot and Ltrans. Torque is found by the cross product of force and r and then torque is used to update the total angular momentum as the comet orbits the Sun. The code prints the final total angular momentum after the specified time t using the angular momentum principle to update angular momentum as the comet goes along its orbit. | |||
== Examples == | == Examples == | ||
'''Simple''' | |||
[[File:simpleam.jpg]] | |||
A simple example of the angular momentum principle is an ice skater spinning about her own center of mass. Remember that change in total angular momentum equals torque times the change in time. Since there is no force being applied to the ice skater, there is no torque on the system and therefore final total angular momentum equals initial total angular momentum. In this case there is no translational angular momentum since the ice skater is not moving and is only spinning in one spot. This simplifies the problem because total angular momentum is equal to rotational angular momentum. Since rotational angular momentum is equal to inertia times angular velocity, the final total angular momentum (rotational angular momentum equals inertia times angular velocity) equals initial total angular momentum. Since inertia of the skater changes from the initial to final state, angular velocity must compensate for this change. Inertia is equal to 1/2 times mass times radius squared. In the initial state, the skater has her arms and legs outstretched therefore giving her a larger radius than in the final state. So when she pulls her legs and arms in her angular velocity (w) increases to compensate for her smaller radius (since the total angular momentum must be the same in the initial and final states) and therefore when her legs and arms are tucked in she spins much faster. | |||
'''Middle''' | |||
[[File:middle1.png]] | |||
[[File:middle2.png]] | |||
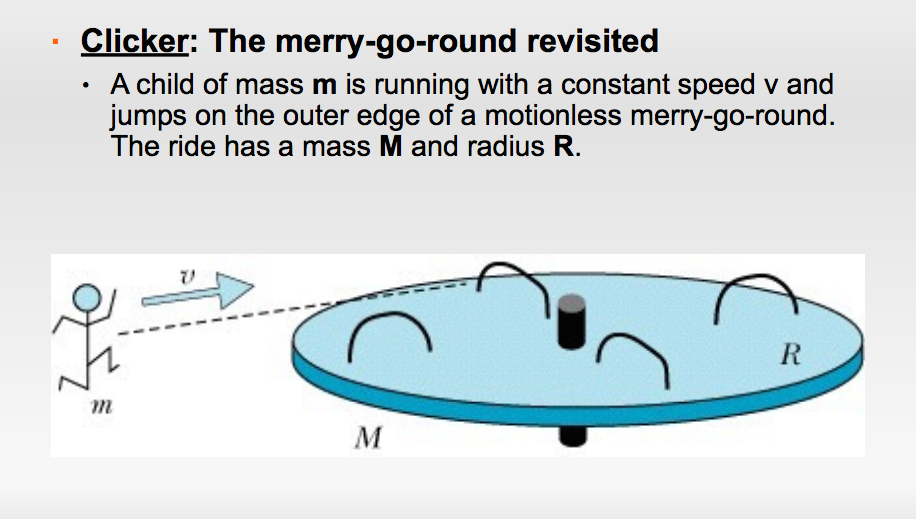
When a child runs and jumps on a playground disk, the child has initial translational angular momentum but no rotational angular momentum (since he is not rotating about his own axis as he runs) and the disk has no initial angular momentum since it is at rest. Once the child jumps on, the child still has translational angular momentum (although its not the same as initial) and the disk has both rotational and translational angular momentum. Once again there is no force acting on the system so there is no torque and final total angular momentum equals initial total angular momentum. Initial total angular momentum is just equal to the translational angular momentum of the child (which is equal to R (the distance from the child to the disk) times momentum of the child (mass times velocity)). Final total angular momentum is equal to the sum of the translational L of the child, rotational L of the child and rotational L of the disk. The final translational L of the child is equal to R times the momentum (mv) where velocity is equal to angular velocity of the disk times R. The final rotational L of the disk is equal to inertia times angular velocity (inertia=1/2 times mass times radius squared). The final rotational L of the child is negligible and can be ignored since the inertia of the child is essentially zero. To find the final speed of the disk and child after the collision, rearrange the variables and solve for w as seen above. This is an example of how to find angular velocity using the angular momentum principle. | |||
'''Difficult''' | |||
[[File:difficult1.png]] | |||
[[File:difficult2.png]] | |||
For part A of this problem, initially the wheel is rotating clockwise and the professor is at rest. Then the professor turns the wheel over so its rotating counterclockwise. Initially there is only rotational angular momentum of the wheel since the professor is at rest. In the final state, both the wheel and professor have rotational angular momentum. Substituting in all the variables for inertia and angular velocity (keeping in mind the direction of the angular velocity), you can solve for the angular velocity of the professor in the final state. In part B, the initial state is the same as part A but the final state now includes translational angular momentum of the wheel since the wheel is held away from the professor's body. Since there is zero torque, set the final total angular momentum equal to the initial total angular momentum and solve for the final angular velocity of the professor. In part C, there is a force applied to the wheel and so therefore you can't ignore torque. Since the wheel comes to rest, the final total angular momentum equals zero so negative initial total angular momentum (solved for in part A) equals torque times change in time. Torque is equal to the force applied times the distance from the wheel axis to the point of force application. Rearranging these variables, you can solve for the change in time. | |||
== Connectedness == | == Connectedness == | ||
The angular momentum principle not only applies to large scale systems like planets orbiting but also to electrons in atoms. The angular momentum principle is used to determine the quantization of electrons in an atom. | |||
[[File:nucleus.png]] | |||
[[File:nucleus2.png]] | |||
Angular momentum also applies to biology through walking locomotion. In the paper by Herr and Popovic, it was found that angular momentum is highly regulated throughout the walking cycle about all three spatial directions. This paper found that whole-body angular momentum is small, despite substantial segmental momenta, indicating large segment-to-segment cancellations. Specifically, the paper show that adjacent leg-segment momenta are balanced in the medio-lateral direction (left foot momentum cancels right foot momentum, etc.). Further, pelvis and abdomen momenta are balanced by leg, chest and head momenta in the anterior–posterior direction, and leg momentum is balanced by upper-body momentum in the vertical direction. | |||
[[File:biology.png]] | |||
== History == | == History == | ||
Isaac Newton first mentions the angular momentum principle in his examples of the [https://en.wikipedia.org/wiki/Newton%27s_laws_of_motion link First Law of Motion] and his geometric proof of [https://en.wikipedia.org/wiki/Kepler%27s_laws_of_planetary_motion#Second_law Law of Areas] indirectly proves angular momentum conservation in the case of a central force. After Newton, Leonhard Euler, Daniel Bernoulli, and Patrick d'Arcy all understood angular momentum in terms of conservation of areal velocity, a result of their analysis of Kepler's Second Law of planetary motion. In 1736 Euler, like Newton, touched on some of the equations of angular momentum. Bernoulli wrote in a 1744 letter of a "moment of rotational motion", possibly the first conception of angular momentum as we now understand it. In 1799, Pierre-Simon Laplace first realized that a fixed plane was associated with rotation — his invariable plane. Louis Poinsot in 1803 began representing rotations as a line segment perpendicular to the rotation, and elaborated on the "conservation of moments". William J. M. Rankine's 1858 Manual of Applied Mechanics defined angular momentum in the modern sense for the first time: | |||
"...a line whose length is proportional to the magnitude of the angular momentum, and whose direction is perpendicular to the plane of motion of the body and of the fixed point, and such, that when the motion of the body is viewed from the extremity of the line, the radius-vector of the body seems to have right-handed rotation." | |||
In fact, Cajori's well-known "History of physics" (1929 edition) gives exactly half a line to angular momentum conservation. However, after the rise of the theory of quantum physics (Niels Bohr's atomic model (1913)) the conservation of angular momentum gained importance since angular momentum and quantum physics are thus clearly linked. | |||
[[File:bohratommoel.gif]] | |||
== See also == | == See also == | ||
[http:///www.physicsbook.gatech.edu/Torque Torque] | |||
[http://www.physicsbook.gatech.edu/Total_Angular_Momentum Total Angular Momentum] | |||
== Further reading == | == Further reading == | ||
Elementary Theory of Angular Momentum by M.E. Rose (2011) | |||
Casey, James. “Applying the principle of angular momentum to constrained systems of point masses”. ''American Journal of Physics''. 82, 165–168 (2014). | |||
Williamson, J.C, R.O Torres-Isea and C.A. Kletzing. "Analyzing linear and angular momentum conservation in digital videos of puck collisions". ''American Journal of Physics''. 68, 841 (2000) | |||
Kuerti, G. "On the Derivation of the Principle of Angular Momentum about the Mass Center". ''American Journal of Physics''. 21, 469 (1953) | |||
== External links == | == External links == | ||
https://www.boundless.com/physics/textbooks/boundless-physics-textbook/rotational-kinematics-angular-momentum-and-energy-9/conservation-of-angular-momentum-86/conservation-of-angular-momentum-328-11269/ | |||
https://en.wikipedia.org/wiki/Angular_momentum | |||
http://jeb.biologists.org/content/211/4/467 | |||
http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/qangm.html | |||
http://galileo.phys.virginia.edu/classes/252/Angular_Momentum/Angular_Momentum.html | |||
== References == | == References == | ||
https://www.boundless.com/physics/textbooks/boundless-physics-textbook/rotational-kinematics-angular-momentum-and-energy-9/conservation-of-angular-momentum-86/conservation-of-angular-momentum-328-11269/ | |||
Georgia Tech Physics 2211 (Professor Gumbart) lecture notes | |||
Georgia Tech Physics 2211 Exam 4 Solution Key | |||
Matter and Interactions by Ruth Chabay and Bruce Sherwood (3rd Edition) | |||
Latest revision as of 01:27, 1 December 2015
claimed by rhollman6
The Main Idea
The angular momentum of an object is the product of the moment of inertia and the angular velocity and is a vector quantity. Total angular momentum is equal to the translational angular momentum about a location A plus the rotational angular momentum around the object's center of mass. The angular momentum principle says that derivative of total angular momentum is equal to the torque applied to the object. Torque is equal to the force about a particular location A times the vector from location A to point of application of force (this is a vector product and torque is a vector quantity). Applying a torque to the system changes the angular momentum of the system. The change in angular momentum of a particle relative to location A is equal to the net angular impulse (net torque,A times the change in time). The angular momentum principle is similar to the momentum principle and the angular momentum principle can be used to calculate torque. Angular momentum is conserved so if system gains angular momentum, the surroundings lose that amount. If there is no torque (and therefore no force) applied to the system then the angular impulse is zero and initial angular momentum equals final angular momentum. The angular momentum principle allows you to learn information about initial angular momentum, final angular momentum, change in time and/or torque depending on what variables are known.
A Mathematical Model
Translational angular momentum is equal to the vector cross product of the location from the object pointing to the location A and the momentum of the object. It can also be found by multiplying the magnitude of the distance vector times the magnitude of the momentum vector times the sin of theta (the angle the two vectors make when they are put tail to tail).
Total angular momentum is equal to the sum of translational angular momentum about location A and rotational angular momentum about the object's center of mass. In multi-particle systems, the translational angular momentum is equal to the vector product of the distance of the center of mass to location A and total momentum of the whole system. Rotational angular momentum is equal to the vector product of the distance of particle 1 to center of mass and momentum of particle 1 plus the vector product of distance of particle 2 to center of mass and momentum of particle 2 plus all the particles in the system. If total angular momentum and translational angular momentum are known then rotational angular momentum can be found just by subtracting Ltrans from Ltot and if Ltot and Lrot are known, Ltrans can be found by subtracting Lrot from Ltot.
The total angular momentum of the system plus the total angular momentum of the surroundings is equal to zero and this is called the conservation of angular momentum. Angular momentum is conserved so if system gains angular momentum, the surroundings lose that amount.
The derivative of total angular momentum is equal to the torque around location A.
Torque is equal to the vector product of the distance from location A to the point of the application of the force and the force itself.
Torque can also be found by multiplying the magnitude of the direction vector from location A to the point of application of the force, the magnitude of the force applied and sin of theta. Theta is the angle the two vectors make when they are put tail to tail.
The angular momentum principle states that the change in total angular momentum in a system is equal to the torque applied to the system times the time the torque is applied. If there is no force acting on the system then there is no torque acting on the system so change in total angular momentum of the system is equal to zero.
Another way of writing the angular momentum principle is the final total angular momentum is equal to the initial total angular momentum plus the angular impulse. This is true because the change in total angular momentum is equal to final total angular momentum minus initial total angular momentum and you can add initial total angular momentum to the other side of the equation to get this equation. Once again, if there is no force acting on the system then there is no torque acting on the system and the angular impulse is equal to zero so final total angular momentum equals initial total angular momentum.
For more information- https://www.youtube.com/watch?v=k9IFb3g2e2M
A Computational Model
This vPython code shows how to solve for final total angular momentum of an object (in this case a comet orbiting around the Sun) using the angular momentum principle to update total angular momentum over the course of a certain amount of time. Initial constants were defined- such as the position of the Sun and comet, radii of the Sun and comet, mass of the Sun and comet, initial velocity of the comet, inertia of the comet (inertia for a sphere is equal to 2/5 times the mass of the comet times the radius of the comet squared), angular velocity of the comet about its own axis, force applied to the comet, and G (the gravitational constant). In the while loop, the momentum of the comet is found and the gravitational force of the Sun on the comet is found to update the position of the comet as it orbits the Sun. Next, translational momentum of the comet around the Sun is found by the cross product of the momentum of the comet and r (which is the distance from the comet to the Sun). Rotational angular momentum is found by multiplyng the inertia of the comet with the angular velocity of the comet. Total angular momentum is the sum of Lrot and Ltrans. Torque is found by the cross product of force and r and then torque is used to update the total angular momentum as the comet orbits the Sun. The code prints the final total angular momentum after the specified time t using the angular momentum principle to update angular momentum as the comet goes along its orbit.
Examples
Simple
A simple example of the angular momentum principle is an ice skater spinning about her own center of mass. Remember that change in total angular momentum equals torque times the change in time. Since there is no force being applied to the ice skater, there is no torque on the system and therefore final total angular momentum equals initial total angular momentum. In this case there is no translational angular momentum since the ice skater is not moving and is only spinning in one spot. This simplifies the problem because total angular momentum is equal to rotational angular momentum. Since rotational angular momentum is equal to inertia times angular velocity, the final total angular momentum (rotational angular momentum equals inertia times angular velocity) equals initial total angular momentum. Since inertia of the skater changes from the initial to final state, angular velocity must compensate for this change. Inertia is equal to 1/2 times mass times radius squared. In the initial state, the skater has her arms and legs outstretched therefore giving her a larger radius than in the final state. So when she pulls her legs and arms in her angular velocity (w) increases to compensate for her smaller radius (since the total angular momentum must be the same in the initial and final states) and therefore when her legs and arms are tucked in she spins much faster.
Middle
When a child runs and jumps on a playground disk, the child has initial translational angular momentum but no rotational angular momentum (since he is not rotating about his own axis as he runs) and the disk has no initial angular momentum since it is at rest. Once the child jumps on, the child still has translational angular momentum (although its not the same as initial) and the disk has both rotational and translational angular momentum. Once again there is no force acting on the system so there is no torque and final total angular momentum equals initial total angular momentum. Initial total angular momentum is just equal to the translational angular momentum of the child (which is equal to R (the distance from the child to the disk) times momentum of the child (mass times velocity)). Final total angular momentum is equal to the sum of the translational L of the child, rotational L of the child and rotational L of the disk. The final translational L of the child is equal to R times the momentum (mv) where velocity is equal to angular velocity of the disk times R. The final rotational L of the disk is equal to inertia times angular velocity (inertia=1/2 times mass times radius squared). The final rotational L of the child is negligible and can be ignored since the inertia of the child is essentially zero. To find the final speed of the disk and child after the collision, rearrange the variables and solve for w as seen above. This is an example of how to find angular velocity using the angular momentum principle.
Difficult
For part A of this problem, initially the wheel is rotating clockwise and the professor is at rest. Then the professor turns the wheel over so its rotating counterclockwise. Initially there is only rotational angular momentum of the wheel since the professor is at rest. In the final state, both the wheel and professor have rotational angular momentum. Substituting in all the variables for inertia and angular velocity (keeping in mind the direction of the angular velocity), you can solve for the angular velocity of the professor in the final state. In part B, the initial state is the same as part A but the final state now includes translational angular momentum of the wheel since the wheel is held away from the professor's body. Since there is zero torque, set the final total angular momentum equal to the initial total angular momentum and solve for the final angular velocity of the professor. In part C, there is a force applied to the wheel and so therefore you can't ignore torque. Since the wheel comes to rest, the final total angular momentum equals zero so negative initial total angular momentum (solved for in part A) equals torque times change in time. Torque is equal to the force applied times the distance from the wheel axis to the point of force application. Rearranging these variables, you can solve for the change in time.
Connectedness
The angular momentum principle not only applies to large scale systems like planets orbiting but also to electrons in atoms. The angular momentum principle is used to determine the quantization of electrons in an atom.
Angular momentum also applies to biology through walking locomotion. In the paper by Herr and Popovic, it was found that angular momentum is highly regulated throughout the walking cycle about all three spatial directions. This paper found that whole-body angular momentum is small, despite substantial segmental momenta, indicating large segment-to-segment cancellations. Specifically, the paper show that adjacent leg-segment momenta are balanced in the medio-lateral direction (left foot momentum cancels right foot momentum, etc.). Further, pelvis and abdomen momenta are balanced by leg, chest and head momenta in the anterior–posterior direction, and leg momentum is balanced by upper-body momentum in the vertical direction.
History
Isaac Newton first mentions the angular momentum principle in his examples of the link First Law of Motion and his geometric proof of Law of Areas indirectly proves angular momentum conservation in the case of a central force. After Newton, Leonhard Euler, Daniel Bernoulli, and Patrick d'Arcy all understood angular momentum in terms of conservation of areal velocity, a result of their analysis of Kepler's Second Law of planetary motion. In 1736 Euler, like Newton, touched on some of the equations of angular momentum. Bernoulli wrote in a 1744 letter of a "moment of rotational motion", possibly the first conception of angular momentum as we now understand it. In 1799, Pierre-Simon Laplace first realized that a fixed plane was associated with rotation — his invariable plane. Louis Poinsot in 1803 began representing rotations as a line segment perpendicular to the rotation, and elaborated on the "conservation of moments". William J. M. Rankine's 1858 Manual of Applied Mechanics defined angular momentum in the modern sense for the first time:
"...a line whose length is proportional to the magnitude of the angular momentum, and whose direction is perpendicular to the plane of motion of the body and of the fixed point, and such, that when the motion of the body is viewed from the extremity of the line, the radius-vector of the body seems to have right-handed rotation."
In fact, Cajori's well-known "History of physics" (1929 edition) gives exactly half a line to angular momentum conservation. However, after the rise of the theory of quantum physics (Niels Bohr's atomic model (1913)) the conservation of angular momentum gained importance since angular momentum and quantum physics are thus clearly linked.
See also
Further reading
Elementary Theory of Angular Momentum by M.E. Rose (2011)
Casey, James. “Applying the principle of angular momentum to constrained systems of point masses”. American Journal of Physics. 82, 165–168 (2014).
Williamson, J.C, R.O Torres-Isea and C.A. Kletzing. "Analyzing linear and angular momentum conservation in digital videos of puck collisions". American Journal of Physics. 68, 841 (2000)
Kuerti, G. "On the Derivation of the Principle of Angular Momentum about the Mass Center". American Journal of Physics. 21, 469 (1953)
External links
https://en.wikipedia.org/wiki/Angular_momentum
http://jeb.biologists.org/content/211/4/467
http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/qangm.html
http://galileo.phys.virginia.edu/classes/252/Angular_Momentum/Angular_Momentum.html
References
Georgia Tech Physics 2211 (Professor Gumbart) lecture notes
Georgia Tech Physics 2211 Exam 4 Solution Key
Matter and Interactions by Ruth Chabay and Bruce Sherwood (3rd Edition)