Wavelength and Frequency: Difference between revisions
Ajohnosn375 (talk | contribs) Created page with " Under Construction By Allie Johnson Short Description of Topic ==The Main Idea== State, in your own words, the main idea for this topic Electric Field of Capacitor ===A M..." |
Ajohnosn375 (talk | contribs) |
||
| (46 intermediate revisions by the same user not shown) | |||
| Line 2: | Line 2: | ||
Under Construction By Allie Johnson | Under Construction By Allie Johnson | ||
Wavelength and Frequency are used to describe a sinusoidal electromagnetic wave. Frequency is the number of peaks per second that pass a given location. Wavelength is the distance between two peaks. | |||
==The Main Idea== | ==The Main Idea== | ||
The frequency of a sinusoidal electromagnetic wave is also the inverse of the period. When that wave is plotted over time, a period will be the distance between two peaks. Frequency is measured in inverse seconds or hertz (Hz). | |||
Wavelength is the distance between two peaks of a sinusoidal electromagnetic wave when plotted over a direction. | |||
[[File:Simplesinewave.jpg|200px|thumb|left|Example of a Wavelength measurement on a simple sine wave]] | |||
Wavelength is directly proportional to frequency. Wavelength is the speed of light divided by the frequency. Therefore, as frequency increases wavelength decreases. This is because over a specific amount of time, the wave will move at the speed of light. Electromagnetic radiation is categorized by its wavelength, spanning from gamma rays to radio waves. | |||
[[File:Electromagneticspectromwavelength.JPG|200px|thumb|right|Types of Electromagnetic Radiation Characterized by Wavelength]] | |||
===A Mathematical Model=== | ===A Mathematical Model=== | ||
===Relationship Between Frequency and Period=== | |||
:<math>f = \frac{1}{T}</math> where '''F''' is the frequency and '''T''' is the period. | |||
===Relationship Between Frequency and Wavelength=== | |||
:<math>f = \frac{c}{\lambda}</math> where '''F''' is the frequency, '''c''' is the speed of light constant (c = 2.998×108 m s−1), and '''lambda''' is the wavelength. | |||
===Relationship Between Frequency and Angular Frequency=== | |||
:<math>\omega = {{2 \pi} \over T} = {2 \pi f} , </math> where '''ω''' is the angular frequency or angular speed (radians per second),'''T''' is the frequency over period (measured in seconds), and '''f''' is the ordinary frequency (measured in hertz). | |||
===A Computational Model=== | ===A Computational Model=== | ||
[[File:Frequencyvswavelengthwave.png|600px|thumb|left|Types of Electromagnetic Radiation Characterized by Wavelength]] | |||
==Examples== | ==Examples== | ||
Conversions to meters per second: | |||
Prefix | |||
p (pico)= 10e-12 | |||
n (nano)= 10e-9 | |||
µ (micro)= 10e-6 | |||
m (milli)= 10e-3 | |||
k (kilo)= 10e3 | |||
M (mega)= 10e6 | |||
G (Giga)= 10e9 | |||
T (Tera)= 10e12 | |||
===Simple=== | ===Simple=== | ||
Problem #1a: Calculate the frequency of radiation with a wavelength of 442 nm. | |||
Example #1b: The wavelength of an argon laser's output is 488.0 nm. Calculate the frequency of this wavelength of electromagnetic radiation. | |||
Solution to 1a: | |||
1) Convert nm to m: | |||
442 nm x (1 m / 109 nm) = 4.42 x 10¯7 m | |||
2) Substitute into λν = c: | |||
(4.42 x 10¯7 m) (x) = 3.00 x 108 m s¯1 | |||
x = 6.79 x 1014 s¯1 | |||
Solution to 1b: | |||
1) Convert nm to m: | |||
488 nm x (1 m / 109 nm) = 4.88 x 10¯7 m | |||
Then, substitute into λν = c: | |||
(4.88 x 10¯7 m) (x) = 3.00 x 108 m s¯1 | |||
x = 6.15 x 1014 s¯1 | |||
The use of nm for wavelength is quite common. | |||
===Middling=== | ===Middling=== | ||
Problem #2a: Calculate the frequency of electromagnetic radiation that has a wavelength of 1.315 micrometers. | |||
Problem #2b: What is the frequency of infrared radiation of wavelength 67.5 μm? | |||
Solution to 2a: | |||
1) Convert μm to m: | |||
1.315 μm x (1 m / 106 μm) = 1.315 x 10¯6 m | |||
2) Substitute into λν = c: | |||
(1.315 x 10¯6 m) (x) = 3.00 x 108 m s¯1 | |||
x = 2.28 x 1014 s¯1 | |||
Solution to 2b: | |||
1) Convert μm to m: | |||
67.5 μm = 67.5 x 10-6 m | |||
2) Use λν = c to determine the frequency: | |||
(67.5 x 10-6 m) (x) = 3.00 x 108 m/s | |||
x = 4.44 x 1012 s-1 | |||
===Difficult=== | ===Difficult=== | ||
Problem #3a: Calculate the frequency of radiation with a wavelength of 4.92 cm. | |||
Problem #3b: Calculate the frequency of radiation with a wavelength of 4.55 x 10¯9 cm. | |||
Comment: since the wavelengths are already in cm, we can use c = 3.00 x 1010 cm s¯1 and not have to do any conversions at all. | |||
Solution to 3a: | |||
(4.92 cm) (x) = 3.00 x 1010 cm s¯1 | |||
x = 6.10 x 109 s¯1 | |||
Solution to 3b: | |||
(4.55 x 10¯9 cm) (x) = 3.00 x 1010 cm s¯1 | |||
x = 6.59 x 1018 s¯ | |||
==Connectedness== | ==Connectedness== | ||
Frequency and Wavelength relate to cancer risk testing. For example, imaging and radiology like x-rays and other like Computed tomography (CT) scans, Magnetic resonance imaging (MRI) scans, Mammography, and Ultrasound save millions of lives by detecting cancer and aid in formulating treatment plans. Each of these tests requires a very specific wavelength and frequency to take images. These medical machines that use electromagnetic waves are directly related to the biomedical engineering field. | |||
==History== | ==History== | ||
Maxwell's theory of electromagnetism (1865) stated that there where electromagnetic waves moving at the speed of light. Maxwell concluded that light itself was just such a wave. After this famous book many scientists tried to detect this electromagnetic radiation using various electrical apparatuses. | |||
In 1886, Heinrich Hertz tried to prove Maxwell's theory with his own electrical apparatus. He made a high voltage induction coil, a capacitor and a spark gap to cause a spark discharge between the spark gap’s two poles which moved back and forth at a frequency determined the capacitor and the induction coil. | |||
. | |||
== See also == | == See also == | ||
For more interest in the movement of sinusoidal waves over time visit: | |||
http://www.physicsbook.gatech.edu/Electromagnetic_Propagation | |||
For interest in how wave length and frequency relate to radiation visit: | |||
http://www.physicsbook.gatech.edu/Sinusoidal_Electromagnetic_Radiaton | |||
===Further reading=== | ===Further reading=== | ||
Chabay, Ruth W., and Bruce A. Sherwood. Matter & Interactions. 3rd ed. Hoboken, NJ: Wiley, 2011. Print | |||
===External links=== | ===External links=== | ||
https://www.youtube.com/watch?v=tJW_a6JeXD8 | |||
==References== | ==References== | ||
"Heinrich Hertz: The Discovery of Radio Waves." Heinrich Hertz: The Discovery of Radio Waves. Web. 3 Dec. 2015 http://www.juliantrubin.com/bigten/hertzexperiment.html | |||
Chabay, Ruth W., and Bruce A. Sherwood. Matter & Interactions. 3rd ed. Hoboken, NJ: Wiley, 2011. Print | |||
Latest revision as of 16:37, 3 December 2015
Under Construction By Allie Johnson
Wavelength and Frequency are used to describe a sinusoidal electromagnetic wave. Frequency is the number of peaks per second that pass a given location. Wavelength is the distance between two peaks.
The Main Idea
The frequency of a sinusoidal electromagnetic wave is also the inverse of the period. When that wave is plotted over time, a period will be the distance between two peaks. Frequency is measured in inverse seconds or hertz (Hz). Wavelength is the distance between two peaks of a sinusoidal electromagnetic wave when plotted over a direction.
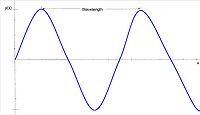
Wavelength is directly proportional to frequency. Wavelength is the speed of light divided by the frequency. Therefore, as frequency increases wavelength decreases. This is because over a specific amount of time, the wave will move at the speed of light. Electromagnetic radiation is categorized by its wavelength, spanning from gamma rays to radio waves.

A Mathematical Model
Relationship Between Frequency and Period
- [math]\displaystyle{ f = \frac{1}{T} }[/math] where F is the frequency and T is the period.
Relationship Between Frequency and Wavelength
- [math]\displaystyle{ f = \frac{c}{\lambda} }[/math] where F is the frequency, c is the speed of light constant (c = 2.998×108 m s−1), and lambda is the wavelength.
Relationship Between Frequency and Angular Frequency
- [math]\displaystyle{ \omega = {{2 \pi} \over T} = {2 \pi f} , }[/math] where ω is the angular frequency or angular speed (radians per second),T is the frequency over period (measured in seconds), and f is the ordinary frequency (measured in hertz).
A Computational Model

Examples
Conversions to meters per second:
Prefix
p (pico)= 10e-12
n (nano)= 10e-9
µ (micro)= 10e-6
m (milli)= 10e-3
k (kilo)= 10e3
M (mega)= 10e6
G (Giga)= 10e9
T (Tera)= 10e12
Simple
Problem #1a: Calculate the frequency of radiation with a wavelength of 442 nm. Example #1b: The wavelength of an argon laser's output is 488.0 nm. Calculate the frequency of this wavelength of electromagnetic radiation.
Solution to 1a:
1) Convert nm to m:
442 nm x (1 m / 109 nm) = 4.42 x 10¯7 m 2) Substitute into λν = c:
(4.42 x 10¯7 m) (x) = 3.00 x 108 m s¯1 x = 6.79 x 1014 s¯1
Solution to 1b:
1) Convert nm to m:
488 nm x (1 m / 109 nm) = 4.88 x 10¯7 m Then, substitute into λν = c:
(4.88 x 10¯7 m) (x) = 3.00 x 108 m s¯1 x = 6.15 x 1014 s¯1
The use of nm for wavelength is quite common.
Middling
Problem #2a: Calculate the frequency of electromagnetic radiation that has a wavelength of 1.315 micrometers. Problem #2b: What is the frequency of infrared radiation of wavelength 67.5 μm?
Solution to 2a:
1) Convert μm to m:
1.315 μm x (1 m / 106 μm) = 1.315 x 10¯6 m 2) Substitute into λν = c:
(1.315 x 10¯6 m) (x) = 3.00 x 108 m s¯1 x = 2.28 x 1014 s¯1
Solution to 2b:
1) Convert μm to m:
67.5 μm = 67.5 x 10-6 m 2) Use λν = c to determine the frequency:
(67.5 x 10-6 m) (x) = 3.00 x 108 m/s x = 4.44 x 1012 s-1
Difficult
Problem #3a: Calculate the frequency of radiation with a wavelength of 4.92 cm. Problem #3b: Calculate the frequency of radiation with a wavelength of 4.55 x 10¯9 cm.
Comment: since the wavelengths are already in cm, we can use c = 3.00 x 1010 cm s¯1 and not have to do any conversions at all.
Solution to 3a:
(4.92 cm) (x) = 3.00 x 1010 cm s¯1 x = 6.10 x 109 s¯1
Solution to 3b:
(4.55 x 10¯9 cm) (x) = 3.00 x 1010 cm s¯1 x = 6.59 x 1018 s¯
Connectedness
Frequency and Wavelength relate to cancer risk testing. For example, imaging and radiology like x-rays and other like Computed tomography (CT) scans, Magnetic resonance imaging (MRI) scans, Mammography, and Ultrasound save millions of lives by detecting cancer and aid in formulating treatment plans. Each of these tests requires a very specific wavelength and frequency to take images. These medical machines that use electromagnetic waves are directly related to the biomedical engineering field.
History
Maxwell's theory of electromagnetism (1865) stated that there where electromagnetic waves moving at the speed of light. Maxwell concluded that light itself was just such a wave. After this famous book many scientists tried to detect this electromagnetic radiation using various electrical apparatuses.
In 1886, Heinrich Hertz tried to prove Maxwell's theory with his own electrical apparatus. He made a high voltage induction coil, a capacitor and a spark gap to cause a spark discharge between the spark gap’s two poles which moved back and forth at a frequency determined the capacitor and the induction coil.
.
See also
For more interest in the movement of sinusoidal waves over time visit: http://www.physicsbook.gatech.edu/Electromagnetic_Propagation
For interest in how wave length and frequency relate to radiation visit: http://www.physicsbook.gatech.edu/Sinusoidal_Electromagnetic_Radiaton
Further reading
Chabay, Ruth W., and Bruce A. Sherwood. Matter & Interactions. 3rd ed. Hoboken, NJ: Wiley, 2011. Print
External links
https://www.youtube.com/watch?v=tJW_a6JeXD8
References
"Heinrich Hertz: The Discovery of Radio Waves." Heinrich Hertz: The Discovery of Radio Waves. Web. 3 Dec. 2015 http://www.juliantrubin.com/bigten/hertzexperiment.html Chabay, Ruth W., and Bruce A. Sherwood. Matter & Interactions. 3rd ed. Hoboken, NJ: Wiley, 2011. Print