Potential Difference Path Independence: Difference between revisions

From Physics Book
Jump to navigation Jump to search
No edit summary
No edit summary
 
(26 intermediate revisions by the same user not shown)
Line 1: Line 1:
By: Amanda L
The potential difference <math>\Delta V = V_B - V_A</math> between two locations A and B does not depend on the path taken between the locations.  
The potential difference <math>\Delta V = V_B - V_A</math> between two locations A and B does not depend on the path taken between the locations.  


Claimed alanghauser3
 
==The Main Idea==
==The Main Idea==


The potential difference between two locations A and B does not depend on the path taken between the locations. A round trip potential difference is always zero.
The potential difference between two locations A and B does not depend on the path taken between the locations. A round trip potential difference is always zero.


===A Mathematical Model===
===Potential Difference Equations===
In a uniform electric field the potential difference is equal to  
In a uniform electric field the potential difference is equal to
:<math>\Delta V</math> = -<math>\vec{E}</math>●<math>\Delta \vec{l}</math> = = -(Ex●<math>\Delta x</math> + Ey●<math>\Delta y</math> + Ez●<math>\Delta z</math>), units = Volts (V)
<math>\Delta V = -\vec{E}●\Delta \vec{l} = -(E_x●\Delta x + E_y●\Delta y + E_z●\Delta z</math>).
 
In a nonuniform electric field the potential difference is equal to  
In a nonuniform electric field the potential difference is equal to  
<math> \textstyle\int\limits_{i}^{f}-Edl </math>
<math> \textstyle\int\limits_{i}^{f}-Edl </math>
Line 16: Line 19:
===Simple Example of Two Different Paths===
===Simple Example of Two Different Paths===
Calculate the potential difference going from A to C: <math>\Delta V = V_C - V_A =  ?</math>
Calculate the potential difference going from A to C: <math>\Delta V = V_C - V_A =  ?</math>
[[File:figure16.30.png|thumb|none|alt=Angled Path.|Angled Path.]]
==Middling===
===Difficult===


==Connectedness==
'''''Path 1'''''
#How is this topic connected to something that you are interested in?
[[File:figure16.30.png|thumb|none|alt=Potential Difference Path Independence.|Angled Path.]] Since the electric field inside the capacitor is uniform all along the path we can use the equation for a uniform electric field <math>\Delta V = -\vec{E}●\Delta \vec{l} = -(E_x●\Delta x + E_y●\Delta y + E_z●\Delta z</math>)
#How is it connected to your major?
The displacement vector:
#Is there an interesting industrial application?
<math>\Delta l = <\Delta x, \Delta y, \Delta z> = <(x_1 - 0),(-y_1 - 0)> = <(x_1,-y_1)></math>
 
The electric field vector is given as:
<math>\vec{E} = <(E_x,0,0)></math>
Therefore the potential difference between A and C is:
<math>\Delta V = -\vec{E}●\Delta \vec{l} = -E_x(x_1) + 0(-y_1) + 0(0) = -E_xx_1</math>
 
'''''Path 2'''''
[[File:figure16.31.png|thumb|none|alt=Potential Difference Path Independence.|Path 2]]
Along the path from A to B:
 
The displacement vector:
<math>\Delta l = <\Delta x, \Delta y, \Delta z> = <(x_1 - 0),(0 - 0)> = <(x_1,0)></math>
 
The potential difference between A and B is:
<math>V_B - V_A = -\vec{E}●\Delta \vec{l} = -E_x(x_1) + 0(0) + 0(0) = -E_xx_1</math>
 
Along the path from B to C:
 
The displacement vector:
<math>\Delta l = <\Delta x, \Delta y, \Delta z> = <(x_1 - x_1),(0 - y_1)> = <(0,-y_1)></math>
 
The potential difference between B and C is:
<math>V_C - V_B = -\vec{E}●\Delta \vec{l} = -E_x(0) + 0(-y_1) + 0(0) = 0</math>


==History==
Therefore the potential difference from A to C is:
<math>\Delta V = (V_B - V_A) + (V_C - V_B) = -E_xx_1 + 0 = -E_xx_1</math>
 
===Two Different Paths Near a Point Charge===
Along a straight path from a point charge Q we know that
<math>\Delta V = \frac{1}{4 \pi \epsilon_0 }Q(\frac{1}{r_2} - \frac{1}{r_1})</math>
 
'''''Path 2'''''
[[File:figure16.32.png|thumb|none|alt=Potential Difference Path Independence|Complicated Path]]
From the initial point <math>i</math> to point <math>A</math>, <math>\vec{E}</math> is perpendicular to <math>\Delta l</math> so <math>\Delta V_1 = 0</math>
 
From <math>A</math> to <math>B</math>:
<math>\Delta V_2 = \frac{1}{4 \pi \epsilon_0 }Q(\frac{1}{r_3} - \frac{1}{r_1})</math>
 
From <math>B</math> to <math>C</math>:
<math>\Delta V_3 = 0</math>, since <math>\vec{E}</math> is perpendicular to <math>\Delta l</math>.
 
From C to <math>f</math>:
<math>\Delta V_4 = \frac{1}{4 \pi \epsilon_0 }Q(\frac{1}{r_2} - \frac{1}{r_3})</math>
 
To find <math>V_f - V_i</math> add up all the <math>\Delta V's</math>
 
<math>V_f - V_i = \Delta V_1 + \Delta V_2 + \Delta V_3 + \Delta V_4</math>
 
<math>= 0 + \frac{1}{4 \pi \epsilon_0 }Q(\frac{1}{r_3} - \frac{1}{r_1}) + 0 + \frac{1}{4 \pi \epsilon_0 }Q(\frac{1}{r_2} - \frac{1}{r_3})</math>
 
<math>= \frac{1}{4 \pi \epsilon_0 }Q(\frac{1}{r_2} - \frac{1}{r_1})</math>
 
===Round Trip Potential Difference===
Since the only points that matter when calculating the potential difference are the initial and final locations, then the round trip potential of any path will equal <math>0</math> since the initial and final locations are the same.
 
Take for example this very simple circuit:
[[File:circuit.png|thumb|none|alt=Potential Difference Path Independence|Simple Circuit]]
 
The potential produced by the battery is equivalent to its <math>emf</math>.
 
Since circuits obey the conservation of energy the potential difference across the whole circuit must equal <math>0</math>
 
Therefore:
<math>\Delta V = V_b + V_w = emf + (-EL) = 0</math>


Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.


== See also ==
== See also ==


Are there related topics or categories in this wiki resource for the curious reader to explore?  How does this topic fit into that context?
Electric Field of a Point Charge
 
Electric Field of a Capacitor


===Further reading===
Potential Difference in a Uniform Field
 
Potential Difference of a point charge in a non-Uniform Field


Books, Articles or other print media on this topic


===External links===
===External links===


Internet resources on this topic
http://www.physicsclassroom.com/class/circuits/Lesson-1/Electric-Potential-Difference
 
https://en.wikipedia.org/wiki/Voltage


==References==
==References==


This section contains the the references you used while writing this page
Chabay, R., & Sherwood, B. (2015). Electric Potential. In Matter & interactions (4th ed., Vol. Two, pp. 644 - 648). Danvers, Massachusetts: J. Wiley & sons.


[[Category:Which Category did you place this in?]]
[[Category:Which Category did you place this in?]]

Latest revision as of 16:01, 1 December 2015

By: Amanda L

The potential difference [math]\displaystyle{ \Delta V = V_B - V_A }[/math] between two locations A and B does not depend on the path taken between the locations.


The Main Idea

The potential difference between two locations A and B does not depend on the path taken between the locations. A round trip potential difference is always zero.

Potential Difference Equations

In a uniform electric field the potential difference is equal to [math]\displaystyle{ \Delta V = -\vec{E}●\Delta \vec{l} = -(E_x●\Delta x + E_y●\Delta y + E_z●\Delta z }[/math]).

In a nonuniform electric field the potential difference is equal to [math]\displaystyle{ \textstyle\int\limits_{i}^{f}-Edl }[/math]

Examples

Simple Example of Two Different Paths

Calculate the potential difference going from A to C: [math]\displaystyle{ \Delta V = V_C - V_A =  ? }[/math]

Path 1

Error creating thumbnail: sh: /usr/bin/convert: No such file or directory Error code: 127
Angled Path.

Since the electric field inside the capacitor is uniform all along the path we can use the equation for a uniform electric field [math]\displaystyle{ \Delta V = -\vec{E}●\Delta \vec{l} = -(E_x●\Delta x + E_y●\Delta y + E_z●\Delta z }[/math])

The displacement vector: [math]\displaystyle{ \Delta l = \lt \Delta x, \Delta y, \Delta z\gt = \lt (x_1 - 0),(-y_1 - 0)\gt = \lt (x_1,-y_1)\gt }[/math]

The electric field vector is given as: [math]\displaystyle{ \vec{E} = \lt (E_x,0,0)\gt }[/math]

Therefore the potential difference between A and C is: [math]\displaystyle{ \Delta V = -\vec{E}●\Delta \vec{l} = -E_x(x_1) + 0(-y_1) + 0(0) = -E_xx_1 }[/math]

Path 2

Error creating thumbnail: sh: /usr/bin/convert: No such file or directory Error code: 127
Path 2

Along the path from A to B:

The displacement vector: [math]\displaystyle{ \Delta l = \lt \Delta x, \Delta y, \Delta z\gt = \lt (x_1 - 0),(0 - 0)\gt = \lt (x_1,0)\gt }[/math]

The potential difference between A and B is: [math]\displaystyle{ V_B - V_A = -\vec{E}●\Delta \vec{l} = -E_x(x_1) + 0(0) + 0(0) = -E_xx_1 }[/math]

Along the path from B to C:

The displacement vector: [math]\displaystyle{ \Delta l = \lt \Delta x, \Delta y, \Delta z\gt = \lt (x_1 - x_1),(0 - y_1)\gt = \lt (0,-y_1)\gt }[/math]

The potential difference between B and C is: [math]\displaystyle{ V_C - V_B = -\vec{E}●\Delta \vec{l} = -E_x(0) + 0(-y_1) + 0(0) = 0 }[/math]

Therefore the potential difference from A to C is: [math]\displaystyle{ \Delta V = (V_B - V_A) + (V_C - V_B) = -E_xx_1 + 0 = -E_xx_1 }[/math]

Two Different Paths Near a Point Charge

Along a straight path from a point charge Q we know that [math]\displaystyle{ \Delta V = \frac{1}{4 \pi \epsilon_0 }Q(\frac{1}{r_2} - \frac{1}{r_1}) }[/math]

Path 2

Error creating thumbnail: sh: /usr/bin/convert: No such file or directory Error code: 127
Complicated Path

From the initial point [math]\displaystyle{ i }[/math] to point [math]\displaystyle{ A }[/math], [math]\displaystyle{ \vec{E} }[/math] is perpendicular to [math]\displaystyle{ \Delta l }[/math] so [math]\displaystyle{ \Delta V_1 = 0 }[/math]

From [math]\displaystyle{ A }[/math] to [math]\displaystyle{ B }[/math]: [math]\displaystyle{ \Delta V_2 = \frac{1}{4 \pi \epsilon_0 }Q(\frac{1}{r_3} - \frac{1}{r_1}) }[/math]

From [math]\displaystyle{ B }[/math] to [math]\displaystyle{ C }[/math]: [math]\displaystyle{ \Delta V_3 = 0 }[/math], since [math]\displaystyle{ \vec{E} }[/math] is perpendicular to [math]\displaystyle{ \Delta l }[/math].

From C to [math]\displaystyle{ f }[/math]: [math]\displaystyle{ \Delta V_4 = \frac{1}{4 \pi \epsilon_0 }Q(\frac{1}{r_2} - \frac{1}{r_3}) }[/math]

To find [math]\displaystyle{ V_f - V_i }[/math] add up all the [math]\displaystyle{ \Delta V's }[/math]

[math]\displaystyle{ V_f - V_i = \Delta V_1 + \Delta V_2 + \Delta V_3 + \Delta V_4 }[/math]

[math]\displaystyle{ = 0 + \frac{1}{4 \pi \epsilon_0 }Q(\frac{1}{r_3} - \frac{1}{r_1}) + 0 + \frac{1}{4 \pi \epsilon_0 }Q(\frac{1}{r_2} - \frac{1}{r_3}) }[/math]

[math]\displaystyle{ = \frac{1}{4 \pi \epsilon_0 }Q(\frac{1}{r_2} - \frac{1}{r_1}) }[/math]

Round Trip Potential Difference

Since the only points that matter when calculating the potential difference are the initial and final locations, then the round trip potential of any path will equal [math]\displaystyle{ 0 }[/math] since the initial and final locations are the same.

Take for example this very simple circuit:

Potential Difference Path Independence
Simple Circuit

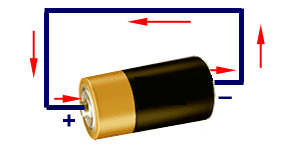
The potential produced by the battery is equivalent to its [math]\displaystyle{ emf }[/math].

Since circuits obey the conservation of energy the potential difference across the whole circuit must equal [math]\displaystyle{ 0 }[/math]

Therefore: [math]\displaystyle{ \Delta V = V_b + V_w = emf + (-EL) = 0 }[/math]


See also

Electric Field of a Point Charge

Electric Field of a Capacitor

Potential Difference in a Uniform Field

Potential Difference of a point charge in a non-Uniform Field


External links

http://www.physicsclassroom.com/class/circuits/Lesson-1/Electric-Potential-Difference

https://en.wikipedia.org/wiki/Voltage

References

Chabay, R., & Sherwood, B. (2015). Electric Potential. In Matter & interactions (4th ed., Vol. Two, pp. 644 - 648). Danvers, Massachusetts: J. Wiley & sons.

Retrieved from "http://www.physicsbook.gatech.edu/index.php?title=Potential_Difference_Path_Independence&oldid=6528"