Charged Cylinder: Difference between revisions
Jburkhardt6 (talk | contribs) |
Jburkhardt6 (talk | contribs) No edit summary |
||
| (30 intermediate revisions by the same user not shown) | |||
| Line 17: | Line 17: | ||
The amount of charge on one of the rods, assuming that the cylinder is complete, is given by: | The amount of charge on one of the rods, assuming that the cylinder is complete, is given by: | ||
<math>dQ = Q\frac{dθ}{ | <math>dQ = Q\frac{dθ}{θ_{total}} = \frac{Qdθ}{θ_{total}}</math> | ||
<math>dθ</math> is the angular width of one rod, and <math> | <math>dθ</math> is the angular width of one rod, and <math>θ_{total}</math> is the angular extent of the cylinder. | ||
The contribution of this individual rod to the total electric field,, assuming that the cylinder is complete, is: | The contribution of this individual rod to the total electric field,, assuming that the cylinder is complete, is: | ||
<math>\Delta \vec{E} = |\Delta \vec{E}|\vec{r} ≈ \frac{1}{4π\epsilon_0} \frac{2dQ}{L} \frac{1}{R} <0,-sinθ,-cosθ> = \frac{1}{4π\epsilon_0} \frac{2}{LR} \frac{Qdθ}{ | <math>\Delta \vec{E} = |\Delta \vec{E}| \vec{r} ≈ \frac{1}{4π\epsilon_0} \frac{2dQ}{L} \frac{1}{R} <0,-sinθ,-cosθ> = \frac{1}{4π\epsilon_0} \frac{2}{LR} \frac{Qdθ}{θ_{total}} <0,-sinθ,-cosθ> </math> | ||
To find the total electric field from all of the rods, the integral of the electric field will have to be taken from the <i>x</i>, <i>y</i>, and <i>z</i> components separately. | To find the total electric field from all of the rods, the integral of the electric field will have to be taken from the <i>x</i>, <i>y</i>, and <i>z</i> components separately. | ||
<math>E_x = \int\limits_0^{ | <math>E_x = \int\limits_0^{θ_{total}}\ \frac{1}{4π\epsilon_0} \frac{2}{LR} \frac{Q}{θ_{total}} * 0dθ = 0</math> | ||
<math>E_y = \int\limits_{0}^{ | <math>E_y = \int\limits_{0}^{θ_{total}}\ \frac{1}{4π\epsilon_0} \frac{2}{LR} \frac{Q}{θ_{total}} * (-sinθ)dθ = \frac{1}{4π\epsilon_0} \frac{2Q}{LRθ_{total}} cosθ|_{0}^{θ_{total}}</math> | ||
<math>E_z = \int\limits_{0}^{ | <math>E_z = \int\limits_{0}^{θ_{total}}\ \frac{1}{4π\epsilon_0} \frac{2}{LR} \frac{Q}{θ_{total}} * (-cosθ)dθ = \frac{-1}{4π\epsilon_0} \frac{2Q}{LRθ_{total}} sinθ|_{0}^{θ_{total}}</math> | ||
=====Without Approximation===== | =====Without Approximation===== | ||
The location vector from the center of a rod can be determined in terms of the angle θ. | |||
<math>\vec{r} = <0,0,0> - <0,R*sinθ,R*cosθ> = <0,-R*sinθ,-R*cosθ></math> | |||
<math>\hat{r} = \frac{\vec{r}}{r} = <0,-sinθ,-cosθ></math> | |||
The amount of charge on one of the rods, assuming that the cylinder is complete, is given by: | |||
<math>dQ = Q\frac{dθ}{θ_{total}} = \frac{Qdθ}{θ_{total}}</math> | |||
<math>dθ</math> is the angular width of one rod, and <math>θ_{total}</math> is the angular extent of the cylinder. | |||
The contribution of this individual rod to the total electric field, is: | |||
<math>\Delta \vec{E} = |\Delta \vec{E}| \vec{r} = \frac{1}{4π\epsilon_0}\frac{dQ}{R*sqrt(R^2+(L/2)^2)} <0,-sinθ,-cosθ> = \frac{1}{4π\epsilon_0} \frac{1}{R*sqrt(R^2+(L/2)^2)} \frac{Qdθ}{θ_{total}} <0,-sinθ,-cosθ></math> | |||
To find the total electric field from all of the rods, the integral of the electric field will have to be taken from the <i>x</i>, <i>y</i>, and <i>z</i> components separately. | |||
<math>E_x = \int\limits_0^{θ_{total}}\ \frac{1}{4π\epsilon_0} \frac{1}{R*sqrt(R^2+(L/2)^2)} \frac{Q}{θ_{total}} * 0dθ = 0</math> | |||
<math>E_y = \int\limits_{0}^{θ_{total}}\ \frac{1}{4π\epsilon_0} \frac{1}{R*sqrt(R^2+(L/2)^2)} \frac{Q}{θ_{total}} * (-sinθ)dθ = \frac{1}{4π\epsilon_0} \frac{1}{R*sqrt(R^2+(L/2)^2)} \frac{Q}{θ_{total}} cosθ|_{0}^{θ_{total}}</math> | |||
<math>E_z = \int\limits_{0}^{θ_{total}}\ \frac{1}{4π\epsilon_0} \frac{1}{R*sqrt(R^2+(L/2)^2)} \frac{Q}{θ_{total}} * (-cosθ)dθ = \frac{1}{4π\epsilon_0} \frac{1}{R*sqrt(R^2+(L/2)^2)} \frac{Q}{θ_{total}} sinθ|_{0}^{θ_{total}}</math> | |||
===Uniformly Charged Rings=== | ===Uniformly Charged Rings=== | ||
| Line 39: | Line 62: | ||
If measuring the electric field of a cylinder from an observation point that is away from the cylinder in the z-direction (assuming that the circles the cylinder is composed of reside in the x-y plane), the method of rings will be most useful. | If measuring the electric field of a cylinder from an observation point that is away from the cylinder in the z-direction (assuming that the circles the cylinder is composed of reside in the x-y plane), the method of rings will be most useful. | ||
===== | Reconfigure the middle of the cylinder (<math>L/2</math>) to be the origin of the coordinate system, making your observation location <math><0,0,w></math> away from the center of the cylinder. | ||
=====z≫R, z≫L===== | |||
The location vector from the observation location to a representative ring of charge at location <math><0,0,z></math> is: | |||
<math>\vec{r} = <0,0,w> - <0,0,z> = <0,0,w-z></math> | |||
The amount of charge on the representative ring at location <math><0,0,z></math> with length <math>dz</math> can be found through: | |||
<math>\frac{Q}{L} = \frac{dQ}{dz}</math> | |||
<math>dQ = \frac{Qdz}{L}</math> | |||
The electric field from a single ring, on axis, can be approximated as: | |||
<math>|\vec{E}_{ring}| ≈ \frac{Q}{4π\epsilon_0} (\frac{1}{z^2}-\frac{3R^2}{2z^4})</math> | |||
Therefore, the electric field from the portion of the cylinder can be found, making the substitution for <math>w-z</math> (found through the location vector) instead of <math>z</math>, to be: | |||
<math>\Delta \vec{E} = |\Delta \vec{E}| \hat{z} ≈ \frac{dQ}{4π\epsilon_0} (\frac{1}{(w-z)^2}-\frac{3R^2}{2(w-z)^4}) \hat{z} = \frac{Qdz}{4π\epsilon_0L} (\frac{1}{(w-z)^2}-\frac{3R^2}{2(w-z)^4}) \hat{z}</math> | |||
The x and y components of <math>\vec{E}_{net}</math> will be zero, because the symmetry of the rings will cancel those components out. Therefore, the z component of <math>\vec{E}_{net}</math> is the only one that needs to be computed through integration. The limits of integration, because the coordinate system was changed to be at the center of the cylinder, are <math>\frac{L}{2}</math> and <math>-\frac{L}{2}</math>. | |||
<math>E_z = \int\limits_{-L/2}^{L/2}\ \frac{Qdz}{4π\epsilon_0L} (\frac{1}{(w-z)^2}-\frac{3R^2}{2(w-z)^4})</math> | |||
To make the integration easier, <math>r</math> can be substituted in for <math>w-z</math>, and <math>dr</math> can be substituted for <math>dz</math>. It is important to remember that <math>w-z</math> is the variable we are integrating through, and therefore a more correct form of <math>dz</math> is <math>d(w-z)</math>, making this a viable substitution. With these substitutions, the new equation to be integrated is: | |||
<math>E_z = \int\limits_{w-L/2}^{w+L/2}\ \frac{Qdr}{4π\epsilon_0L} (\frac{1}{r^2}-\frac{3R^2}{2r^4}) = \frac{Qdr}{4π\epsilon_0L} \int\limits_{w-L/2}^{w+L/2}\ (\frac{1}{r^2}-\frac{3R^2}{2r^4}) dr = \frac{Q}{4π\epsilon_0L} [(-r)^{-1}|_{w-L/2}^{w+L/2} - \frac{3R^2}{2} (-\frac{r^{-3}}{3}|_{w-L/2}^{w+L/2}) ] </math> | |||
<math> E_z = \frac{Q}{4π\epsilon_0L} [\frac{R^2}{2}((w+\frac{L}{2})^{-3})- (w+\frac{L}{2})^{-3}))-((w+\frac{L}{2})^{-1})- (w+\frac{L}{2})^{-1}))]</math> | |||
==Examples== | ==Examples== | ||
===Easy=== | |||
[[File:Cylinderview.png|300px|thumb|right|View of the cylinder, z-axis coming out of the page.]] | |||
For a positively charged half cylinder, projected on the z-axis, what would the direction of the net electric field be at the center? | |||
====Solution==== | ====Solution==== | ||
<math> | The portions of the cylinder along the positive and negative z axis would cancel out, making <math>E_{z}</math> equal to zero by symmetry. The cylinder is also symmetric about the x-axis, making <math>E_{x}</math> equal to zero as well. By the right hand rule, a positive charge that is above the observation location creates a field in the negative direction away from the observation location. | ||
<math> | Therefore, <math>E_{net} = <0,-\hat{y},0></math> | ||
===Middling=== | ===Middling=== | ||
Find the net electric field at the center of the half cylinder from the easy example above that is 2 meters long, has a radius of .05 meters, and has a 3 Coulomb charge. | |||
====Solution==== | ====Solution==== | ||
= | We can use the approximated formula of a ring, since the observation location is at the center and 2≫.05. | ||
<math>θ_{total} = π</math> | |||
== | <math>dQ = Q\frac{dθ}{π} = \frac{Qdθ}{π}</math> | ||
== | <math>\vec{r} = <0,0,0> - < R*cosθ,R*sinθ,0> = <-R*cosθ,-R*sin,0></math> | ||
<math>\hat{r} = \frac{\vec{r}}{r} = <-cosθ,-sin,0></math> | |||
== | <math>E_x = \int\limits_{0}^{π}\ \frac{1}{4π\epsilon_0} \frac{2}{LR} \frac{Q}{π} * (-cosθ)dθ = \frac{-1}{4π\epsilon_0} \frac{2Q}{LRπ} sinθ|_{0}^{π} = 0</math> | ||
<math>E_y = \int\limits_{0}^{π}\ \frac{1}{4π\epsilon_0} \frac{2}{LR} \frac{Q}{π} * (-sinθ)dθ = \frac{1}{4π\epsilon_0} \frac{2Q}{LRπ} -cosθ|_{0}^{π} = \frac{1}{4π\epsilon_0} \frac{2}{LR} \frac{Q}{π} * -2 = (9*10^9) \frac{(-4)(3)}{(2)(.05)(π)} = -3.44*10^{11}</math> | |||
<math>E_z= \int\limits_0^{π}\ \frac{1}{4π\epsilon_0} \frac{2}{LR} \frac{Q}{π} * 0dθ = 0</math> | |||
= | <math>\vec{E}_{net} = <0,-3.44*10^{11},0> N/C </math> | ||
This answer aligns with the answer achieved above. | |||
== | == See also == | ||
http://www.physicsbook.gatech.edu/Electric_Field | |||
http://www.physicsbook.gatech.edu/Charged_Ring | |||
http://www.physicsbook.gatech.edu/Charged_Rod | |||
Latest revision as of 19:03, 5 December 2015
Electric Field
Topic reserved by Jennifer Burkhardt
The electric field of a uniformly charged cylinder of length [math]\displaystyle{ L }[/math] and radius [math]\displaystyle{ R }[/math] can be found through viewing the cylinder as a collection of long uniformly charged rods forming a circle or a series of uniformly charged rings stacked on top of another. Before determining which method to use, the point of observation must be decided.
Uniformly Charged Rods
If measuring the electric field of a cylinder from an observation point that is at the center of the cylinder, the method of rods would be most useful.
L≫R
The location vector from the center of a rod can be determined in terms of the angle θ.
[math]\displaystyle{ \vec{r} = \lt 0,0,0\gt - \lt 0,R*sinθ,R*cosθ\gt = \lt 0,-R*sinθ,-R*cosθ\gt }[/math] [math]\displaystyle{ \hat{r} = \frac{\vec{r}}{r} = \lt 0,-sinθ,-cosθ\gt }[/math]
The amount of charge on one of the rods, assuming that the cylinder is complete, is given by:
[math]\displaystyle{ dQ = Q\frac{dθ}{θ_{total}} = \frac{Qdθ}{θ_{total}} }[/math]
[math]\displaystyle{ dθ }[/math] is the angular width of one rod, and [math]\displaystyle{ θ_{total} }[/math] is the angular extent of the cylinder.
The contribution of this individual rod to the total electric field,, assuming that the cylinder is complete, is:
[math]\displaystyle{ \Delta \vec{E} = |\Delta \vec{E}| \vec{r} ≈ \frac{1}{4π\epsilon_0} \frac{2dQ}{L} \frac{1}{R} \lt 0,-sinθ,-cosθ\gt = \frac{1}{4π\epsilon_0} \frac{2}{LR} \frac{Qdθ}{θ_{total}} \lt 0,-sinθ,-cosθ\gt }[/math]
To find the total electric field from all of the rods, the integral of the electric field will have to be taken from the x, y, and z components separately.
[math]\displaystyle{ E_x = \int\limits_0^{θ_{total}}\ \frac{1}{4π\epsilon_0} \frac{2}{LR} \frac{Q}{θ_{total}} * 0dθ = 0 }[/math]
[math]\displaystyle{ E_y = \int\limits_{0}^{θ_{total}}\ \frac{1}{4π\epsilon_0} \frac{2}{LR} \frac{Q}{θ_{total}} * (-sinθ)dθ = \frac{1}{4π\epsilon_0} \frac{2Q}{LRθ_{total}} cosθ|_{0}^{θ_{total}} }[/math]
[math]\displaystyle{ E_z = \int\limits_{0}^{θ_{total}}\ \frac{1}{4π\epsilon_0} \frac{2}{LR} \frac{Q}{θ_{total}} * (-cosθ)dθ = \frac{-1}{4π\epsilon_0} \frac{2Q}{LRθ_{total}} sinθ|_{0}^{θ_{total}} }[/math]
Without Approximation
The location vector from the center of a rod can be determined in terms of the angle θ.
[math]\displaystyle{ \vec{r} = \lt 0,0,0\gt - \lt 0,R*sinθ,R*cosθ\gt = \lt 0,-R*sinθ,-R*cosθ\gt }[/math] [math]\displaystyle{ \hat{r} = \frac{\vec{r}}{r} = \lt 0,-sinθ,-cosθ\gt }[/math]
The amount of charge on one of the rods, assuming that the cylinder is complete, is given by:
[math]\displaystyle{ dQ = Q\frac{dθ}{θ_{total}} = \frac{Qdθ}{θ_{total}} }[/math]
[math]\displaystyle{ dθ }[/math] is the angular width of one rod, and [math]\displaystyle{ θ_{total} }[/math] is the angular extent of the cylinder.
The contribution of this individual rod to the total electric field, is:
[math]\displaystyle{ \Delta \vec{E} = |\Delta \vec{E}| \vec{r} = \frac{1}{4π\epsilon_0}\frac{dQ}{R*sqrt(R^2+(L/2)^2)} \lt 0,-sinθ,-cosθ\gt = \frac{1}{4π\epsilon_0} \frac{1}{R*sqrt(R^2+(L/2)^2)} \frac{Qdθ}{θ_{total}} \lt 0,-sinθ,-cosθ\gt }[/math]
To find the total electric field from all of the rods, the integral of the electric field will have to be taken from the x, y, and z components separately.
[math]\displaystyle{ E_x = \int\limits_0^{θ_{total}}\ \frac{1}{4π\epsilon_0} \frac{1}{R*sqrt(R^2+(L/2)^2)} \frac{Q}{θ_{total}} * 0dθ = 0 }[/math]
[math]\displaystyle{ E_y = \int\limits_{0}^{θ_{total}}\ \frac{1}{4π\epsilon_0} \frac{1}{R*sqrt(R^2+(L/2)^2)} \frac{Q}{θ_{total}} * (-sinθ)dθ = \frac{1}{4π\epsilon_0} \frac{1}{R*sqrt(R^2+(L/2)^2)} \frac{Q}{θ_{total}} cosθ|_{0}^{θ_{total}} }[/math]
[math]\displaystyle{ E_z = \int\limits_{0}^{θ_{total}}\ \frac{1}{4π\epsilon_0} \frac{1}{R*sqrt(R^2+(L/2)^2)} \frac{Q}{θ_{total}} * (-cosθ)dθ = \frac{1}{4π\epsilon_0} \frac{1}{R*sqrt(R^2+(L/2)^2)} \frac{Q}{θ_{total}} sinθ|_{0}^{θ_{total}} }[/math]
Uniformly Charged Rings
If measuring the electric field of a cylinder from an observation point that is away from the cylinder in the z-direction (assuming that the circles the cylinder is composed of reside in the x-y plane), the method of rings will be most useful.
Reconfigure the middle of the cylinder ([math]\displaystyle{ L/2 }[/math]) to be the origin of the coordinate system, making your observation location [math]\displaystyle{ \lt 0,0,w\gt }[/math] away from the center of the cylinder.
z≫R, z≫L
The location vector from the observation location to a representative ring of charge at location [math]\displaystyle{ \lt 0,0,z\gt }[/math] is:
[math]\displaystyle{ \vec{r} = \lt 0,0,w\gt - \lt 0,0,z\gt = \lt 0,0,w-z\gt }[/math]
The amount of charge on the representative ring at location [math]\displaystyle{ \lt 0,0,z\gt }[/math] with length [math]\displaystyle{ dz }[/math] can be found through:
[math]\displaystyle{ \frac{Q}{L} = \frac{dQ}{dz} }[/math] [math]\displaystyle{ dQ = \frac{Qdz}{L} }[/math]
The electric field from a single ring, on axis, can be approximated as:
[math]\displaystyle{ |\vec{E}_{ring}| ≈ \frac{Q}{4π\epsilon_0} (\frac{1}{z^2}-\frac{3R^2}{2z^4}) }[/math]
Therefore, the electric field from the portion of the cylinder can be found, making the substitution for [math]\displaystyle{ w-z }[/math] (found through the location vector) instead of [math]\displaystyle{ z }[/math], to be:
[math]\displaystyle{ \Delta \vec{E} = |\Delta \vec{E}| \hat{z} ≈ \frac{dQ}{4π\epsilon_0} (\frac{1}{(w-z)^2}-\frac{3R^2}{2(w-z)^4}) \hat{z} = \frac{Qdz}{4π\epsilon_0L} (\frac{1}{(w-z)^2}-\frac{3R^2}{2(w-z)^4}) \hat{z} }[/math]
The x and y components of [math]\displaystyle{ \vec{E}_{net} }[/math] will be zero, because the symmetry of the rings will cancel those components out. Therefore, the z component of [math]\displaystyle{ \vec{E}_{net} }[/math] is the only one that needs to be computed through integration. The limits of integration, because the coordinate system was changed to be at the center of the cylinder, are [math]\displaystyle{ \frac{L}{2} }[/math] and [math]\displaystyle{ -\frac{L}{2} }[/math].
[math]\displaystyle{ E_z = \int\limits_{-L/2}^{L/2}\ \frac{Qdz}{4π\epsilon_0L} (\frac{1}{(w-z)^2}-\frac{3R^2}{2(w-z)^4}) }[/math]
To make the integration easier, [math]\displaystyle{ r }[/math] can be substituted in for [math]\displaystyle{ w-z }[/math], and [math]\displaystyle{ dr }[/math] can be substituted for [math]\displaystyle{ dz }[/math]. It is important to remember that [math]\displaystyle{ w-z }[/math] is the variable we are integrating through, and therefore a more correct form of [math]\displaystyle{ dz }[/math] is [math]\displaystyle{ d(w-z) }[/math], making this a viable substitution. With these substitutions, the new equation to be integrated is:
[math]\displaystyle{ E_z = \int\limits_{w-L/2}^{w+L/2}\ \frac{Qdr}{4π\epsilon_0L} (\frac{1}{r^2}-\frac{3R^2}{2r^4}) = \frac{Qdr}{4π\epsilon_0L} \int\limits_{w-L/2}^{w+L/2}\ (\frac{1}{r^2}-\frac{3R^2}{2r^4}) dr = \frac{Q}{4π\epsilon_0L} [(-r)^{-1}|_{w-L/2}^{w+L/2} - \frac{3R^2}{2} (-\frac{r^{-3}}{3}|_{w-L/2}^{w+L/2}) ] }[/math] [math]\displaystyle{ E_z = \frac{Q}{4π\epsilon_0L} [\frac{R^2}{2}((w+\frac{L}{2})^{-3})- (w+\frac{L}{2})^{-3}))-((w+\frac{L}{2})^{-1})- (w+\frac{L}{2})^{-1}))] }[/math]
Examples
Easy
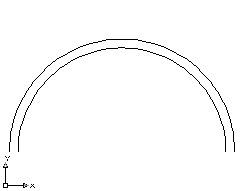
For a positively charged half cylinder, projected on the z-axis, what would the direction of the net electric field be at the center?
Solution
The portions of the cylinder along the positive and negative z axis would cancel out, making [math]\displaystyle{ E_{z} }[/math] equal to zero by symmetry. The cylinder is also symmetric about the x-axis, making [math]\displaystyle{ E_{x} }[/math] equal to zero as well. By the right hand rule, a positive charge that is above the observation location creates a field in the negative direction away from the observation location.
Therefore, [math]\displaystyle{ E_{net} = \lt 0,-\hat{y},0\gt }[/math]
Middling
Find the net electric field at the center of the half cylinder from the easy example above that is 2 meters long, has a radius of .05 meters, and has a 3 Coulomb charge.
Solution
We can use the approximated formula of a ring, since the observation location is at the center and 2≫.05.
[math]\displaystyle{ θ_{total} = π }[/math]
[math]\displaystyle{ dQ = Q\frac{dθ}{π} = \frac{Qdθ}{π} }[/math]
[math]\displaystyle{ \vec{r} = \lt 0,0,0\gt - \lt R*cosθ,R*sinθ,0\gt = \lt -R*cosθ,-R*sin,0\gt }[/math]
[math]\displaystyle{ \hat{r} = \frac{\vec{r}}{r} = \lt -cosθ,-sin,0\gt }[/math]
[math]\displaystyle{ E_x = \int\limits_{0}^{π}\ \frac{1}{4π\epsilon_0} \frac{2}{LR} \frac{Q}{π} * (-cosθ)dθ = \frac{-1}{4π\epsilon_0} \frac{2Q}{LRπ} sinθ|_{0}^{π} = 0 }[/math]
[math]\displaystyle{ E_y = \int\limits_{0}^{π}\ \frac{1}{4π\epsilon_0} \frac{2}{LR} \frac{Q}{π} * (-sinθ)dθ = \frac{1}{4π\epsilon_0} \frac{2Q}{LRπ} -cosθ|_{0}^{π} = \frac{1}{4π\epsilon_0} \frac{2}{LR} \frac{Q}{π} * -2 = (9*10^9) \frac{(-4)(3)}{(2)(.05)(π)} = -3.44*10^{11} }[/math]
[math]\displaystyle{ E_z= \int\limits_0^{π}\ \frac{1}{4π\epsilon_0} \frac{2}{LR} \frac{Q}{π} * 0dθ = 0 }[/math]
[math]\displaystyle{ \vec{E}_{net} = \lt 0,-3.44*10^{11},0\gt N/C }[/math]
This answer aligns with the answer achieved above.
See also
http://www.physicsbook.gatech.edu/Electric_Field